基于时间限制的用户撤销CP-ABE方案∗

迪力夏提·吾普尔，韩舒艳，古丽米热·尔肯，努尔买买提·黑力力

(新疆大学数学与系统科学学院，新疆乌鲁木齐830046)

云存储使用户能够在云中分享数据，但数据拥有者不能完全信任云服务器．因为云服务器可能会遭到破坏或给未经授权用户提供数据，以赚取利益．因此人们采用密文策略属性基加密（CP-ABE,Ciphertext Policy Attribute Based Encryption）方案，加密数据之后把密文存放在云上，与授权用户分享．文献[1-5]对CP-ABE做了相关研究．

CP-ABE很适合在云服务器上使用，但是CP-ABE中实现用户的撤销仍然是一个棘手的问题．撤销用户时，要保证用户不再具有解密数据能力，同时要保证不影响其余未撤销的用户正常访问数据．用户撤销方面有不少研究[6,15]．文献[6]提出了一种具有系统级用户撤销的ABE方案．该方案通过在“与”门上用“非”操作来实现撤销，但效率较低．文献[17]提出了一种利用二叉树实现用户撤销的CP-ABE方案，在密钥生成中心更新密钥来实现撤销，但其性能比较低，而且大大增加了密钥生成中心的计算和通信负担．文献[8]提出了一个CP-ABE的用户撤销方案，在数据加密时密文当中嵌入用户列表来实现用户的直接撤销．文献[9]提出了一种动态用户撤销方案．在云服务器对密文进行重新加密，并且云服务器完全控制用户的撤销列表．当用户撤销列表被发送来时，用户将失去对数据的所有访问权限．文献[10]中提出CP-ABE的属性和用户撤销的方案，其中引入了一个辅助函数来指定涉及到撤销事件的密文，然后使用广播加密技术只更新辅助函数指定的密文来实现属性和用户的直接撤销．文献[11]在智能电网中实现CP-ABE的用户撤销．文献[12]提出CP-ABE的用户撤销，方案中对访问控制树的根节点设置一个有效访问时间来实现用户撤销，但是解密数据的计算量和密钥管理代价较高．

本文在J.Hur等人[4]方案的基础上，提出一种具有隐藏策略的基于时间限制的用户撤销CP-ABE方案，对每个用户指定访问数据的有效期来实现用户撤销．譬如，一个大学将图书馆的电子图书存储在云服务器上，便于学生访问．由于每年都有一部分学生毕业离校，因此需要解决用户撤销的问题．针对此问题，对每个新生指定一个访问数据的有效期（比如学制）．学生一旦毕业有效期就过期，无法继续访问数据，从而实现用户撤销．

1 系统架构

1.1 系统描述

系统流程如图1所示．系统描述如下：

图1 系统流程Fig 1 System work flow

云服务器：提供存储数据和共享数据的服务．

数据拥有者：制定访问控制策略，按策略对数据进行加密生成密文，并将密文放到云服务器，以便于共享数据．

用户：访问云服务器上的数据．只有用户的属性满足访问控制策略，用户才能对密文进行解密并得到明文．

密钥生成中心KGC（Key Generation Center）：对系统生成公共参数，并且对每个用户制定访问数据的时间限制，假设它是半诚实的．KGC执行其它实体分配给它的合法任务，但它可能试图获取数据拥有者的数据．

时间服务器：判断用户访问数据的时间是否过期或者是否被伪造或篡改过．它执行由其它实体分配给它的合法任务，假设它是完全可信的．

代理服务器：使用从时间服务器得到的令牌对数据执行部分解密，假设它是半诚实的．代理服务器执行其它实体分配给它的合法任务，但它可能会试图获取数据拥有者的数据内容和访问控制策略．

1.2 算法结构

方案由Setup、KeyGen、Encryption、GenToken、TimeCheck、SPartDecrypt、Decrypt 7个算法组成．算法步骤如下：

Setup(λ)→(PKKGC,MKKGC),(PKsign,MKsign),(PKS,MKS)：这个算法输入为安全参数λ，KGC为整个系统生成公共参数．KGC输出自己的公私钥对(PKKGC,MKKGC)和(PKsign,MKsign)，代理服务器输出自己的公私钥对(PKS,MKS)．

KeyGen(MKKGC,S,MKsign)→(SKut,Tt,ξ):KGC把MKKGC,PKsign和用户的属性集S作为输入，为用户ut输出私钥SKut的同时，对每个用户制定访问数据的时间限制Tt，并且对时间Tt生成数字签名ξ．

Encryption(Γ,M,PKKGC,PKS)→CT：数据拥有者使用PKKGC,PKS和访问结构树Γ对数据M进行加密，并输出密文CT．

GenToken(SKut,S0,Tt)→BT：用户ut使用私钥SKut和属性集S0⊆S，制作携带时间限制Tt的令牌BT=(TKS0,ut||Tt)，其中TKS0,ut是用户令牌，Tt是为用户ut指定的时间．

TimeCheck(BT,ξ,PKsign)→TKS0,ut：时间服务器收到带着时间限制Tt的令牌BT后，首先判断用户发的时间是否被伪造或篡改过．如果是，返回⊥．否则进一步判断用户的时间是否过期，如果没有过期就把令牌发给代理服务器，否则返回⊥．

SPartDecrypt(CT,TKS0,ut)→ CT′：此算法由代理服务器来执行．以CT和TKS0,ut为输入，如果用户属性S′满足访问控制策略，算法输出部分解密的数据CT′；否则返回⊥．

Decrypt(CT′,SKut)→M：该算法以CT′和SKut为输入，对部分解密的CT′进一步解密，并且输出明文M．

1.3 安全性模型

方案安全性是通过一个挑战者和敌手之间的安全游戏进行定义的，安全游戏步骤如下：初始化阶段：挑战者选择阶为p的两个乘法循环群G0和G1，并且选择哈希函数H:{0,1}→G0，双线性映射e:G0×G0→G1和主密钥β ∈．

提出查询阶段：挑战者把属性λ1,λ2,...,λq给A，A用哈希函数H计算相应的私密钥H(λ1)β,...,H(λq)β，并且返回给A．

挑战阶段：A收集了足够的信息以后，挑战者把ga∈G0发给A．

猜测阶段：A猜出属性λi和被模糊化的属性si∈G0,其中λi是提取查询阶段从未查询过的属性．

攻击者的优势可以定义为Adv(A)=Pr[e(ga,H(λi))β=si]．如果A运行的时间不超过t并且优势为ε，我们可以说A是以(t,ε)赢得安全游戏．假设有一个对手A赢了安全游戏．我们现在可以构造一个算法B，A利用它来能解决BDH问题．

定理1如果在安全游戏中多项式时间内得到的优势可以忽略不计，那么我们的方案是安全的．

2 密码方案

2.1 预备知识

定义1(访问结构)假设{p1,p2,...,pn}是一个实体集，A⊆2{p1,p2,...,pn}{∅}是访问结构．如果对∀B,C都会有B∈A，且B⊆C，即C∈A，则称A是单调的．

定义2(双线性对)设G0和G1是阶为素数p的乘法循环群，g是G0的生成元素．映射e:G0×G0→G1是一个双线性对，如果e具有以下特性：

1）对∀u,v∈G0，∀x,y∈，有e(ux,vy)=e(u,v)xy;

2）对∀g∈G0，有e(g,g)6=1．这里1代表G1群的单位元;

3）计算e:G0×G0→G1是有效的．

定义3（DBDH问题）基于上述概念，给出了G0的生成元g和元素gx,gy,gz，其中∀x,y,z∈，DBDH问题是计算出e(g,g)xyz．

2.2 方案描述

设G0是一个阶为素数p的双线性群，g是G0的生成元．设e:G0×G0→G1为双线性映射．安全参数λ将决定双线性群的大小．我们选取三个哈希函数：H:{0,1}→G0，H1:G1→{0,1}logp和H2:{0,1}∗→{0,1}∗．并且定义拉格朗日系数

Setup(λ)→(PKKGC,MKKGC),(PKS,MKS),(PKsign,MKsign)：KGC和代理服务器生成自己的公钥和私钥对．

KGC选择阶为素数p的循环群G0和G1，g是G0和G1的生成元．KGC选择一些公共参数和哈希函数：(G0,g,H,H1,H2)，其中H:{0,1}→G0，H1:G1→{0,1}logp，H2:{0,1}∗→{0,1}∗．

keyGen(MKKGC,S,MKsign)→(SKut,Tt,ξ)：KGC对用户ut和属性λj分别任意选取唯一和保密的随机数rt∈和rj∈，然后为用户生成私钥：

最后为每个用户指定限制访问数据的时间Tt，并且对时间Tt进行数字签名

Encryption(Γ,M,PKKGC,PKS)→CT：数据拥有者ua将明文M共享之前，使用访问控制树Γ对数据进行加密．对于访问控制树的详细内容请查看文献[1]．设Y为访问控制树Γ中所有叶子节点的集合，算法任意选取随机指数a∈，对y∈Y计算Sy=e((gβ)a,H(λy))，然后计算H1(Sy)，并且访问控制树中的属性λy都被H1(Sy)替换掉，为了加密明文M计算会话密钥KS=e((gγ)a,H(IDS))，最终密文如下：

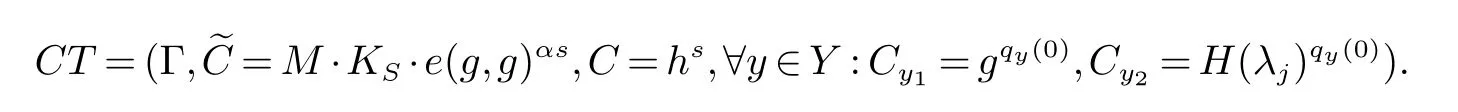
数据拥有者ua将(IDa,ga,CT)发给云服务器．

GenToken(SKut,S′,Tt)→BT：用户ut发送请求从代理服务器获取ga，然后对每个属性λj∈S′，计算Sj=e(ga,)=e(ga,H(λj)β)．此算法任意选取一个随机数τ∈，并为具有属性集S′的用户ut制造令牌：TKS0,ut=(∀λj∈ S′:Ij=H1(Sj),(Dj)τ,()τ)．然后用户ut从KGC得到的时间限制Tt和制造的令牌TKS0,ut记为BT=(TKS0,ut||Tt)发给时间服务器．

TimeCheck(BT,ξ,PKsign)→TKS0,ut：时间服务器收到带着时间限制的令牌BT后，首先用数字签名技术验证用户是否对KGC发给它的时间Tt进行伪造或篡改过，验证过程如下：

如果验证失败，则返回⊥．如果验证成功，则说明用户没有对KGC发给它的时间伪造或篡改过，即时间服务器把Tt和当地时间进行比较，判断用户访问数据的时间是否过期．如果过期了，则返回⊥．如果没有过期，则时间服务器将令牌发送到代理服务器．

SPartDecrypt(CT,TKS0,ut)→CT′：代理服务器收到令牌之后，要判断令牌中嵌入的属性索引Ij是否跟CT里面的模糊化属性相同．如果是，那么它对访问控制树的叶子节点x开始运行DecryptDode(CT,TKS0,ut,x)递归算法，计算如下：

否则，有DecryptDode(CT,TKS0,ut,x)=⊥．

当x是一个非叶子节点的时候，假设所有节点z是x的子节点，则运行算法Fz=DecryptDode(CT,TKS0,ut,z)．假设Sx是子节点z的集合，使Fx6=⊥．该算法计算如下：

之后，算法是在访问控制树Γ的根节点R开始运行．如果用户的令牌满足访问控制树Γ，则代理服务器运行DecryptDode(CT,TKS0,ut,R)=e(g,g)rtτs．

代理服务器计算会话密钥KS=e(ga,MKS)=e(ga,H(IDS)γ)，然后计算最终将部分解密的数据CT′=(,C=hs,A)发送给用户，其中A=DecryptNode(CT,TKS0,ut,R)=e(g,g)rtτs．

Decrypt(CT′,SKut)→M：用户ut从代理服务器得到密文CT′后，用自己的私钥对密文进行解密．解密过程如下：

最终输出明文M ．

2.3 安全性证明

定理2如果文献［3］的方案在选择明文攻击（CPA，Chosen-plaintext attack）下是安全的，则本文方案在CPA下是安全的．

文献［3］已经证明敌手在多项式时间内得到的优势可以忽略不计，所以本文方案在CPA下是安全的．

定理3如果文献［4］的方案在CPA下是安全的，则本文方案在CPA下是安全的．

文献［4］已经证明敌手在多项式时间内得到的优势可以忽略不计，所以本文方案在CPA下是安全的．

3 方案分析

3.1 数据的机密性

数据的机密性是通过属性来实现的．如果用户属性不能满足访问控制树，就不能成功访问云上的数据．因为用户用自己的属性计算出e(g,g)rtτs，一旦用户属性不满足访问控制树就无法计算出e(g,g)rtτs，从而有效的防止非授权用户的访问数据．

3.2 抗合谋

攻击者为了访问数据先要用自己的属性计算出e(g,g)rtτs．如果没有具备属性λ的攻击者和具备属性λ的用户合谋访问数据是不可能的，因为KGC为每个用户生成唯一的随机数rt来构造密钥，所以即便几个用户合谋也无法计算出e(g,g)rtτs．

3.3 隐藏策略

数据拥有者数据加密的过程中，访问控制树的每一个属性λy都被模糊化属性H1(e((gβ)a,H(λy)))替换掉．因为模糊化属性里面的参数α和β只有授权用户知晓，所以未授权用户和云服务器计算不出H1(e((gβ)a,H(λy)))，从而实现了隐藏策略的目的．

3.4 后向安全

因为KGC对每个用户指定一个有效期．用户每次访问数据的时候都要把有效期和自己的令牌发给时间服务器．当用户访问数据时，不仅他的令牌要满足访问控制树，而且他访问数据的时间在有效期内才能成功的对数据进行解密．一旦有效期到期，用户的私钥将不再有效，就无法访问数据，从而保证后向安全性．

3.5 理论分析和比较

表1中对几个关于用户撤销方案的撤销制度、隐藏策略特性、重新加密阶段和密钥更新阶段进行了比较．从表1可以看到本文相对其他三个用户撤销方案的优点．与文献[6-8]三个方案相比，本文没有重新加密阶段和密钥更新阶段，因此降低了整个算法的计算量．此外本文具备隐藏策略的特性．

表1 功能比较Tab 1 Capability comparison

表2 存储成本比较表Tab 2 Storage cost comparison

表2对几个方案中的密文长度、公钥长度和密钥长度进行比较．其中C0和C1分别表示群G0和群G1中元素的长度，t表示密文相关的属性个数，k表示用户密钥相关的属性个数，l表示系统中所有属性的个数，r表示被撤销的用户个数．

4 结论

本文提出一种基于时间限制的用户撤销访问控制方案．方案中对每个用户指定访问数据的有效期来实现高效安全的用户撤销，因此省略重加密阶段和更新密钥阶段．为了防止指定时间的篡改和伪造，使用了短签名方法，从而大大减少整个算法的计算量．此外对访问控制树的每个属性进行隐藏，从而避免了访问控制策略泄漏敏感信息．本文主要考虑用时间限制来实现用户撤销，下一步工作是用时间限制来实现安全高效的细粒度属性撤销．