新Chua多涡卷混沌吸引子的产生及应用*
贾美美 蒋浩刚 李文静
(内蒙古工业大学电力学院自动化系,呼和浩特 010080)
1 引 言
1986年,Chua等[1]提出了著名的Chua系统,首次在混沌与非线性电路之间架起了一座桥梁,成为了研究混沌系统的一个范例.1993年,Suykens和Vandewalle[2]采用拟线性方法构造了n个双涡卷混沌系统.为了更好地应用于语音保密通信等实际工程中,研究人员开始致力于构造拓扑结构更为复杂和非线性动力学行为更加丰富的多涡卷混沌系统.与传统的双涡卷混沌系统相比,多涡卷混沌系统具有更多的涡卷密钥参数,即数量众多的涡卷能在相空间中呈现出某个方向分布的平面或立体网格状图案,涡卷之间具有相互嵌套的拓扑结构,具有更为复杂的非线性动力学行为.这种复杂性体现在混沌吸引子的相轨迹或状态变量的取值能够在多个不同的涡卷之间随机跳变.2004年,Lü等[3,4]分别采用饱和函数序列和时滞函数序列构造了多涡卷混沌吸引子.2011年,陈仕必等[5]采用多项式和阶跃函数构造了多涡卷混沌吸引子.2014年,艾星星等[6]通过设计切换控制器实现了不同多涡卷混沌吸引子之间的复合.2017年,Hong等[7]利用多脉冲控制技术产生了一系列多涡卷混沌吸引子.2018年,Zhang和Wang[8]采用饱和函数序列和符号函数产生了多涡卷混沌吸引子.除此之外,能够产生多涡卷混沌吸引子的方法还有双曲正切函数序列[9,10]、非线性调制函数序列[11]、阈值函数序列[12]、忆阻器[13−18]等.忆阻器作为一种非线性电子元件,可被看作混沌系统中的非线性项,通过采用忆阻器能够产生多涡卷混沌吸引子.在不改变电路结构的前提条件下,通过改变忆阻器的强度(即可调参数)能够得到不同数量的涡卷[16].本文采用分段非线性对数函数序列构造了一个新Chua多涡卷混沌系统,通过分析其非线性动力学行为,得到了新Chua多涡卷混沌吸引子的产生机制.
许多实际应用中都需要消除或抑制混沌行为,即混沌控制.1990年,Ott等[19]提出了OGY(Ott-Grebogi-Yorke)混沌控制方法,此后,各种混沌控制方法不断涌现.常见的混沌控制方法有脉冲控制法[20,21]、外加周期微扰法[22]、延迟反馈法[23−25]、递归反步控制法[26−29]等.脉冲控制法的控制信号是脉冲式的,难以避免控制间隙外部噪声产生的严重干扰.外加周期微扰法属于非反馈控制,当系统的混沌行为消失后,控制信号仍不为零,通常适合在非自治系统的混沌控制中应用.延迟反馈法在实现混沌控制时不需要确定目标轨道,但其延迟周期难以确定.带有递归反步控制器的非线性系统具有良好的全局稳定性、跟踪性和暂态性能.本文基于李雅普诺夫稳定性理论和反步思想设计三个递归反步控制器,将Chua多涡卷混沌系统中的混沌状态控制到不动点及期望值,从而抑制其中的混沌行为.
由于混沌系统对初始条件的高度敏感性及对噪声的免疫性,使得混沌理论在微弱信号检测领域具有广阔的应用前景.1992年,Birx和Pipenberg[30]将混沌振子与复映射前馈神经网络结合检测淹没在高斯噪声中的微弱信号,为微弱信号检测开辟了新思路.之后,大量学者提出了各种基于Duffing混沌系统或改进型Duffing混沌系统的微弱信号检测方法.但基于这类混沌系统的微弱信号检测方法有一定的局限性,主要为系统由临界混沌状态转变为大尺度周期状态的现象不明显.当待测信号的频率远大于系统本身的频率时,系统就会回到混沌状态,不能保持在临界混沌状态,以至于达不到良好的检测效果.因此,研究基于非Duffing混沌系统的微弱信号检测方法是重要的.2010年,徐艳春和杨春玲[31]、Xu等[32]提出了基于Rossler混沌控制的强噪声背景下单频正弦信号检测方法.2017年,Li和Zhang[33]采用两个混沌同步Chua系统来检测单频微弱正弦信号,不需要跟踪相空间轨迹的改变,只需要得到同步误差.本文提出一种新多频微弱周期信号频率检测方法,即利用Chua多涡卷混沌系统和递归反步控制器对信号的各频率进行检测.首先,判断Chua多涡卷混沌系统是否处于混沌域中的任一混沌状态(不需要处于临界混沌状态); 其次,采用递归反步控制器将处于混沌状态的Chua多涡卷混沌系统控制到不动点; 最后,通过频谱分析检测出信号的各频率.
2 Chua多涡卷混沌系统的产生
2.1 新Chua双涡卷混沌系统
在经典Chua系统的基础上[1,34],提出分段非线性对数函数g(x),用其产生新Chua双涡卷混沌系统,见(1)式.
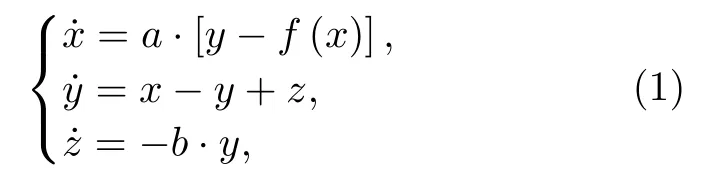
其中a=10 ,b=16 ,f(x)=0.5·x−2.5·g(x).
对数函数g(x)的表达式如下
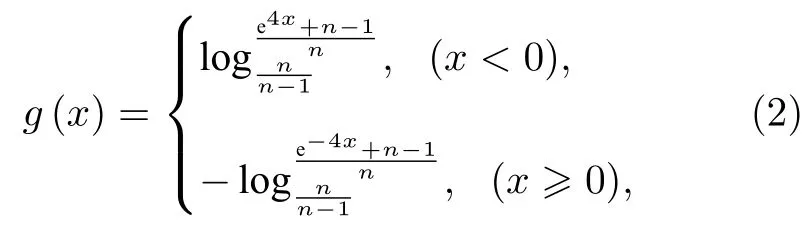
其中n<0 或n>1.当n取不同值时,对数函数g(x)的曲线如图1所示.由图1可知,对数函数g(x)关于原点奇对称,值域为 [−1,1].

图1 对数函数Fig.1.Logarithmic function.
以n=2 为例来研究新Chua双涡卷混沌系统的电路图及物理意义.新Chua双涡卷混沌系统的电路图如图2所示(NR为非线性电阻),其对应的有量纲状态方程由(3)式表示.

有量纲状态方程[(3)式]与无量纲状态方程[(1)式]的对应关系如下: 状态变量的对应关系为系统参数的对应关系为16; 非线性函数的对应关系为f′(vC1)=f(vC1)−vC1=·−0.5vC1·−2.5g(vC1).f′(vC1)是非线性电阻NR的伏安特性.当n=2 时,对数函数g(vC1)的表达式为(4)式.

图2 新Chua双涡卷混沌系统的电路图Fig.2.Circuit diagram of the novel Chua double-scroll chaotic system.

(4)式可改写为
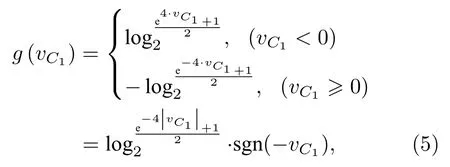
其中 sgn(·)表示符号函数.
以下给出g(vC1)的电路图.图3—图8分别表示的电路图.图中运算放大器的型号为741,T1和T2表示NPN型晶体管,D1和D2表示二极管,电阻R0=R1=R2=R4=R5=R7=R8=R11=R12=R13=R14=R15=R16=R17=R20=R21=R22=10kΩ ,R3=5kΩ,R6=1040Ω ,R9=R10=R23=R24=1MΩ,R18=R19=20kΩ ,R25=.18.02Ω ,R26=R28=1kΩ,R27=13.5kΩ ,直流电压V1=V2=1 V.

图3 |vc1|的电路图Fig.3.Circuit diagram of |vc1|
由图3可得到(6)式.

由图4可得到(7)式—(10)式.

其中VT表示晶体管 T1的温度电压当量,在室温下约为 26mV.

其中晶体管 T1的反向饱和电流Is=1µA.

由图5可得到(11)式、(12)式.
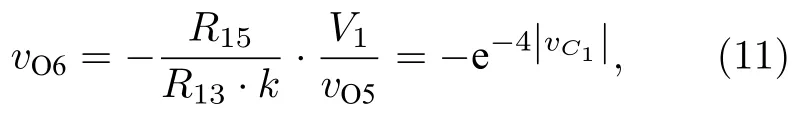
其中乘法器增益k=1.
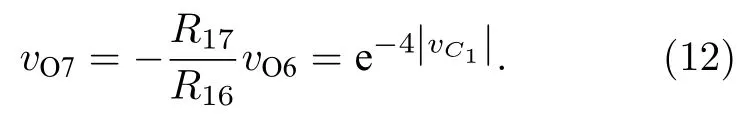
由图6可得到(13)式—(16)式.


图4 e4|vC1| 的电路图Fig.4.Circuit diagram of e4|vC1|.

图5 e−4|vC1| 的电路图Fig.5.Circuit diagram of e−4|vC1|.


其中VT表示晶体管 T2的温度电压当量,在室温下约为 26mV ,晶体管 T2的反向饱和电流Is=1µA.

由图7可得到(17)式、(18)式.

其中运算放大器的输出饱和电压.Esat=13.5V

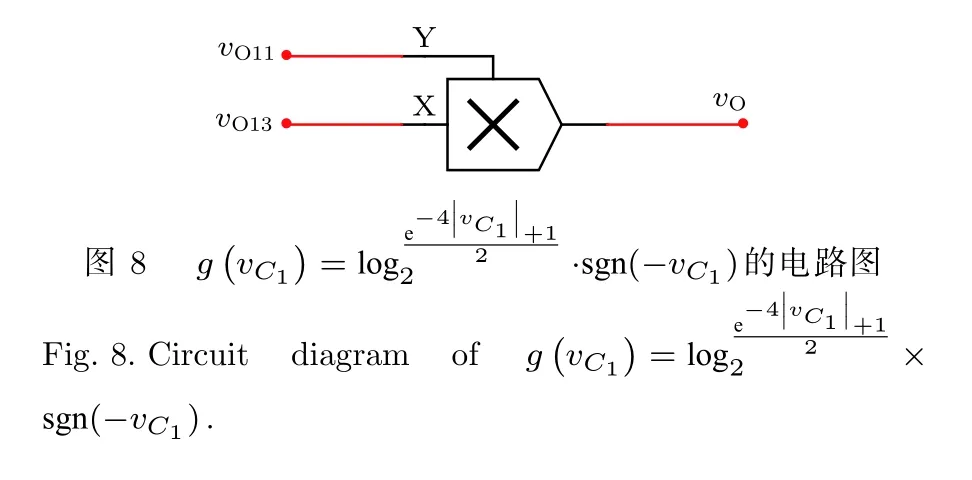
由图8可得到(19)式.

其中乘法器增益k=1.
综上所述,图3—图8组成了对数函数g(vC1)的电路图.
以n=2 为例来分析新Chua双涡卷混沌系统的非线性动力学行为.由(1)式可知,当n=2 时新Chua双涡卷混沌系统的无量纲状态方程为

其中a=10 ,b=16 ,h(x)=0.5·x−2.5·g(x).对数函数g(x)的表达式为

此时新Chua双涡卷混沌系统[(20)式]有3个平衡点:Q0=(0,0,0)和Q±=(±5,0,∓5).平衡点Q±有相同的特征值λ1=−6.2777 和λ2,3=0.1389±i3.5671,表明平衡点Q±是指标2的鞍焦平衡点[1,36,37],用于产生新Chua双涡卷混沌系统[(20)式]中的2个涡卷.平衡点Q0对应的特征值为λ1=67.2809和λ2,3=−0.5730±i3.9544 ,表明平衡点Q0是指标1的鞍焦平衡点[1,36,37],用于连接2个涡卷.
系统(20)式的三个李雅普诺夫指数(Lyapunov exponents,LE)LE1=0.447946 ,LE2=0.000359 和LE3=−5.534524,如图9所示.LE1表明在相空间某一方向上相邻轨道呈指数率分离,系统对初始条件极为敏感,这是混沌突出的特性.LE2是混沌吸引子周期性的表现,其周期为无穷大.LE3表明系统的相体积是收缩的,从而确保系统在整体上的稳定性.由上述三个李雅普诺夫指数可知系统(20)式是混沌的.

图9 系统[(20)式]的李雅普诺夫指数Fig.9.Lyapunov exponents of system(Equation(20)).
根据三个李雅普诺夫指数可得系统(20)式的分维数DL为

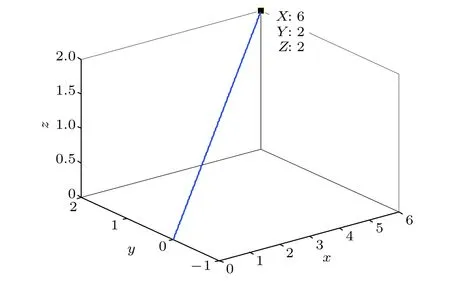
式中 2 新Chua双涡卷混沌系统[(20)式]的相图和时域图如图10所示.图10(a)表示了新Chua双涡卷混沌系统x-y平面的相图,图10(b)表示了新Chua双涡卷混沌系统x方向的时域图. 图10 新Chua双涡卷混沌系统(a)x-y 平面的相图;(b)x方向的时域图Fig.10.Novel Chua double-scroll chaotic system:(a)Phase diagram on the x-y plane;(b)time domain diagram in the x direction. 对数函数序列的电路图与对数函数的电路图类似,在对数函数电路图的基础上,经过拓展平衡点即可得到对数函数序列的电路图,这里不再详述. 在新Chua双涡卷混沌系统的基础上,引入对数函数序列G(x),可得Chua多涡卷混沌系统,见(23)式. 其中a=10 ,b=16 ,H(x)=0.5·x−2.5·G(x).G(x)可表示为 可产生(2M+2)偶数个涡卷, 或 可产生(2N+1)奇数个涡卷. (24)式、(25)式中,M是非负整数,N是正整数,g(·)为(21)式. 当M=N=1 ,对数函数序列(24)式和(25)式分别如图11和图12所示.涡卷的数量由对数函数序列G(x)的片段个数决定.例如,图11中,沿着x方向有4个片段,4个片段对应4个涡卷.图12中,沿着x方向有3个片段,3个片段对应3个涡卷.x-y平面4-涡卷混沌吸引子(M=1)的相图如图13所示.x-z平面12-涡卷混沌吸引子(M=5)的相图如图14所示. 图12 多分段对数函数序列[(25)式],取N=1Fig.12.Multi-segment logarithmic function series(Equation(25))with N=1. 图14 x-z平面12-涡卷混沌吸引子的相图Fig.14.Phase diagram of the 12-scroll chaotic attractor on the x-z plane. 2.3.1 对称性和不变性 在坐标变换(x,y,z)→(−x,−y,−z)下,系统(23)式的微分方程保持不变,即系统(23)式关于原点奇对称. 对于(2M+2)偶数个涡卷混沌吸引子,根据(24)式可得 对于(2N+1)奇数个涡卷混沌吸引子,根据(25)式可得 由(27)式和(28)式可知,系统(23)式的所有平衡点都是沿着x轴和z轴方向分布. 系统(23)式线性化的雅可比矩阵为 (30)式的特征值为 由(31)式可知(30)式有一个正实根和一对有负实部的共轭复根,表明平衡点是指标1的鞍焦平衡点[1,36,37].平衡点也被称为类型Ⅰ的平衡点. (32)式的特征值为 由(33)式可知(32)式有一个负实根和一对有正实部的共轭复根,表明平衡点是指标2的鞍焦平衡点[1,36,37].平衡点也被称为类型Ⅱ的平衡点. 综上所述,系统(23)式可产生(2M+2)偶数个多涡卷混沌吸引子或(2N+1)奇数个多涡卷混沌吸引子. 以12-涡卷混沌吸引子为例,分析其产生机制.表1表示12-涡卷混沌吸引子的平衡点、特征值和平衡点的类型.根据表1的特征值,可知类型Ⅱ的平衡点Q21,22用于产生12个涡卷,类型Ⅰ的平衡点Q0、用于连接12个涡卷. 2.3.3 最大李雅普诺夫指数和庞加莱映射 当b=16 ,a变化时,4-涡卷混沌系统的最大李雅普诺夫指数如图15所示.当a=[8,12] 时,最大李雅普诺夫指数为正,表明4-涡卷混沌系统在该范围内处于混沌状态.对于一个系统是否处于混沌运动状态,也可从庞加莱截面上点的分布情况来判定.若运动状态是混沌的,庞加莱截面上则是一段连续的曲线或是一些成片的密集点,反之,则不是混沌的.4-涡卷混沌系统在x-y平面上的庞加莱映射如图16所示,截面上是连续的曲线和一些成片的密集点,说明当a=10 ,b=16 时系统处于混沌状态. 图15 最大李雅普诺夫指数Fig.15.Largest Lyapunov exponent. 图16 x-y平面的庞加莱映射Fig.16.Poincaré mapping on the x-y plane. 在Chua多涡卷混沌系统(23)式的基础上加入递归反步控制器,可得受控Chua多涡卷混沌系统为 其中Ui(t),i=1,2,3 是控制信号,可使系统状态变量x,y,z分别跟踪期望值xd,yd,zd.定义状态变量和期望值之间的误差状态为 令 其中ci,i=1,2,3 是控制参数,ρ(t)是时间t的光滑函数.将(36)式代入(35)式可得 对(37)式求导,然后将(34)式代入(37)式的导数中,可得误差系统,见(38)式. 为了稳定误差系统(38)式,考虑李雅普诺夫函数为 其中kx、ky、kz是大于零的常数.可得(39)式对时间t的导数为 当c1=c3=1 ,c2=0 时,递归反步控制器U1(t)、U2(t)、U3(t)能够将系统(34)式控制到期望值.将(37)式和(38)式代入(41)式可得递归反步控制器为 以4-涡卷混沌系统为例验证递归反步控制器对混沌行为的控制效果.假设初始条件为(x,y,z)=(6,2,2),系统参数为a=10 ,b=16 ,控制器Ui(t)为(42)式. 图17 状态变量和期望值 [sin(t),0,0] 的时域图(a)x,xd;(b)y,yd;(c)z,zdFig.17.Time domain diagram of state variables and desired values [sin(t),0,0] :(a)x,xd;(b)y,yd;(c)z,zd. 递归反步控制器能够将4-涡卷混沌系统控制到正弦函数ρ(t)=sin(t)如图17所示.图17(a)—(c)分别表示状态变量和期望值 [sin(t),0,0] 的时域图.同理,递归反步控制器可将4-涡卷混沌系统控制到坐标原点如图18所示.图18(a)—(c)分别表示状态变量和期望值(0,0,0)的时域图.由图17、图18可知,施加递归反步控制器后的受控系统能够跟踪正弦函数和原点. 图18 状态变量和期望值(0,0,0)的时域图(a)x,xd;(b)y,yd;(c)z,zdFig.18.Time domain diagram of state variables and desired values(0,0,0):(a)x,xd;(b)y,yd;(c)z,zd. 本节采用Chua多涡卷混沌系统与递归反步控制器相结合的方法来进行微弱信号检测.检测原理: 基于混沌控制理论与Chua多涡卷混沌系统对高斯噪声的免疫性,利用递归反步控制器将含有高斯噪声和待测多频微弱周期信号的Chua多涡卷混沌系统控制到不动点,然后进行频谱分析检测出信号的各频率,检测原理图如图19所示. 图19 检测原理图Fig.19.Detection schematic diagram. 具体检测过程如下: 1)确定系统(23)式的参数,使系统(23)式处于混沌状态. 2)将高斯噪声加入到系统状态方程(23)式的第二项,如果系统(23)式仍处于混沌状态,说明系统(23)式对高斯噪声免疫. 3)采用递归反步控制器(42)式,将系统(23)式控制到不动点. 4)对检测系统(由系统(23)式、三个递归反步控制器(42)式、高斯噪声和待测多频微弱周期信号组成)的输出信号进行频谱分析,检测出高斯噪声背景下待测多频微弱周期信号的各频率. 首先应用随机微分方程理论[38]分析Chua多涡卷混沌系统(23)式对高斯噪声的免疫性.用∆x(t)、∆y(t)、∆z(t)分别表示高斯噪声对x(t)、y(t)、z(t)的小扰动,高斯噪声存在的情况下,系统的状态方程(23)式可写为 其中n(t)是高斯噪声,其期望E[n(t)]=0.(43)式减去(23)式,可得 由于 ∆x很小,可略去(44)式中 ∆x的非线性项(当 ∆x→0 时,−a·H(∆x)→0). 将(44)式表示为矢量微分方程的形式 其中 它的解为 其中 Φ(·)为系统的状态转移矩阵.由于第一项为暂态解,很快衰减为零,因此只考虑第二项,可得 可见,在统计意义下,任何零均值高斯噪声都不会改变原系统的运行轨迹. 将均值为0,方差为0.001的高斯噪声n(t)加入到系统状态方程(23)式的第二项可得 (52)式的相图如图20所示,由该图可知系统的相轨迹几乎没有变化(与图13相比),说明系统对高斯噪声具有免疫性.图20所得结果与上述理论推导一致. 图20 系统[(52)式]的相图Fig.20.Phase diagram of system [Equation(52)]. 将输入信号input=s(t)+n(t)加入到受控系统状态方程(34)式的第二项,可得检测系统为 其中n(t)是均值为0,方差为0.001的高斯噪声.s(t)=A1·sin(2πf1t)+A2·sin(2πf2t)+A3·sin(2πf3t)是待测多频微弱周期信号.幅值A1=A2=A3=0.005,频率f1=0.2 Hz,f2=0.5 Hz,f3=0.7 Hz. 以4-涡卷混沌系统为例,其中a=10 ,b=16 ,初始条件为(6,2,2),此时系统处于混沌状态(见2.3.3节),验证检测方法的有效性.总仿真时间为300 s,当仿真时间为100 s时,将input加入到系统(34)式中.检测系统(53)式的相图如图21所示.由图21可知,三个递归反步控制器可将状态变量从初始条件(6,2,2)控制到原点(0,0,0).控制信号U1(t)、U2(t)、U3(t)的时域图如图22所示,图22(a)是原始图,图22(b)是放大图.由图22可知控制信号U1(t)、U2(t)、U3(t)迅速收敛于0.待测信号的频谱图如图23所示.由图23可知3个频率分别是f1=0.2 Hz,f2=0.5 Hz,f3=0.7 Hz. 图21 检测系统[(53)式]的相图Fig.21.Phase diagram of the detection system [Equation(53)]. 经过计算可得信噪比(signal-to-noise ratio,SNR)为 其中P1为周期信号功率,P2为噪声功率. 在微弱信号检测领域,采用时域方法处理信号的最低SNR只有–10 dB左右[39],而本文采用Chua多涡卷混沌系统和递归反步控制器相结合进行多频微弱周期信号检测得到的最低SNR为–19 dB,提高了检测精度,为基于非Duffing混沌系统的微弱信号检测提供了新思路. 图22 控制信号 U1(t)、U2(t)、U3(t)的时域图(a)原始图;(b)放大图,t=[0,100]sFig.22.Time domain diagram of control signals U1(t)、U2(t)、U3(t):(a)Original diagram(b)enlarging diagram,t=[0,100]s. 图23 待测信号的频谱图Fig.23.Frequency spectrum of the signal to be detected. 本文提出了一种构造多涡卷混沌系统的新非线性函数方法,即对数函数序列法.首先研究了Chua多涡卷混沌系统的非线性动力学行为及其混沌吸引子的产生机制.Chua多涡卷混沌吸引子的产生机制为指标2的鞍焦平衡点用于产生涡卷,指标1的鞍焦平衡点用于连接涡卷.所产生的Chua多涡卷混沌吸引子形状清晰、大小一致,且处于同一水平位置.然后采用三个递归反步控制器抑制了Chua多涡卷混沌系统的混沌行为.最后基于混沌控制理论与Chua多涡卷混沌系统对高斯噪声的免疫性,提出了一种新微弱信号检测方法,即在检测系统中通过采用三个递归反步控制器将处于混沌状态的Chua多涡卷混沌系统控制到不动点来检测信号的各频率.与基于Duffing系统微弱信号检测方法相比,本文提出的检测方法不需要判断系统是否处于临界混沌状态,只需要判断系统是否进入混沌域(在某些系统参数范围内,系统处于混沌状态)即可.以后的工作可采用合适的对数函数序列构造二维及三维多涡卷混沌系统,并将这些多涡卷混沌系统应用到实际的微弱信号检测中.需要注意的是为了进一步提高SNR,可采用一些消噪方法对待测信号进行预处理.
2.2 Chua多涡卷混沌系统





2.3 Chua多涡卷混沌系统的非线性动力学行为










3 Chua多涡卷混沌系统的控制
3.1 递归反步控制器的设计









3.2 仿真结果


4 基于Chua多涡卷混沌系统的微弱信号检测
4.1 检测原理和方法

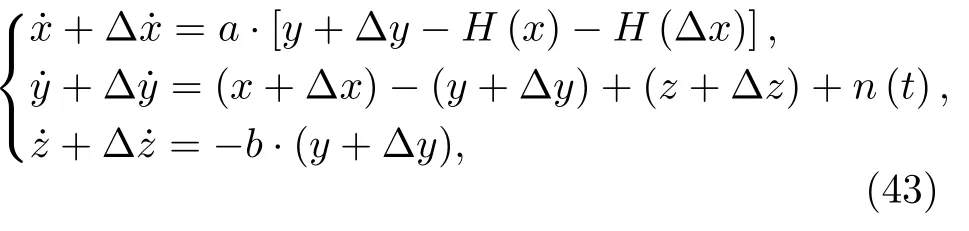
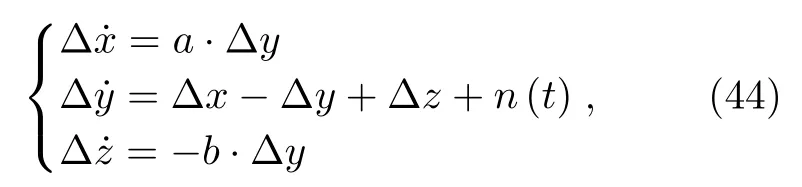






4.2 检测结果




5 结 论

