方差分析教学初探

高文武，张 侠，2*

（1.安徽大学经济学院，安徽合肥230411；2.阜阳师范学院信息工程学院，安徽阜阳236037）

在统计学中，经常会遇到相关关系、因果关系和函数关系[1]，当两个对象有相关关系时，需进一步判断造成这种相关关系的原因，并探索它们之间是否存在因果关系；在研究函数关系时，关键也是判断两个变量之间是否具有因果关系，判断方法主要包括参数统计法（如t-检验、方差分析等）和非参数统计法（如Kruskal-Wallis分析、Friedman分析等）[2]。在实际问题中因变量往往有多个水平，若利用t-检验则需要做多次检验，导致整个过程非常复杂，还会增加出现错误的概率。而方差分析法正是解决这一问题的有效方法。

1 方差分析

方差分析又称“变异数分析”，是英国著名的统计与遗传学家菲希尔提出的一种用于判断变量之间是否存在因果关系的统计方法[3]。它可以有效处理多个水平的因变量问题。从涉及的影响因素个数将方差分析分为单因素方差分析和多因素方差分析[4]，文章主要讨论单因素情形。

假设自变量为X，因变量为Y。方差分析的主要目标是检验X在不同水平（Xi,i=1,2,…,M）上的变动是否对Y有显著影响。其准则为Y的变动主要是由X的变动而造成的，这就需要计算Y的总变动。而真实的Y是未知的，只能利用采样手段获得观测数据，通过样本来计算Y的变动。样本有以下假设：Y服从正态分布，样本之间相互独立且同分布，若假设不成立，则选择非参数检验[5]。方差分析整个过程主要由4个部分构成[6]。

首先，计算Y的总变动SST。总变动是目标变量Y的观测值与平均值之间的波动，它包含由于X在不同水平上的变动所导致的波动、随机噪声导致的波动。令Yˉ为所有观测值的平均值，即Yˉ=根据方差的定义，总变动可表示为其次，计算组间均方和SSY。依据定义，计算Y在对应于水平Xi的观测值的平均值在此基础上可得组间均方和SSY=再次，计算组内均方和SSe。组内均方和是由随机噪声导致的波动，其计算公式为SSe=显然SST=SSY+SSe恒成立。最后，检验Y的总变动SST是否主要由组间均方和SSY构成。这是方差分析的关键一步，它不仅展示了方差分析与假设检验之间的关系，同时也是假设检验的一个具体应用。这里需要比较SSY与SSe的大小关系，而SSY与SSe都是总量指标，无法比较大小。因此，需要把他们标准化后，再比较组间均方和MSY、组内均方和MSe之间的大小，其中MSY=SSY/dfY，MSe=SSe/dfe，这里，dfY=M-1，dfe=∑Ni-M，分别称为组间平方和的自由度和组内平方和的自由度。依据方差分析的基本思想，构建统计量，即F=MSY/MSe。

进一步，组间平方和、组内平方和各自除以总体方差分别服从卡方分布，两个卡方分布分别除以各自自由度再相比构建F-统计量，可知统计量F服从自由度为(dfY,dfe)的F-分布，从而利用假设检验判断X对Y是否有显著性影响。

2 方差分析的应用

为进一步加深对方差分析的认识和应用，明晰其中的分析过程，下面通过两个案例展示方差分析的具体应用。

案例1 根据某高校经济学、财务管理、金融工程、国际商务和中韩财管等5个专业的学生统计学考试分数，探讨专业对于统计学成绩有无显著影响。

用相应公式计算出其各专业统计学分数均值和方差，如表1所示[7]。根据以上方差分析的基本步骤，分析过程如下。

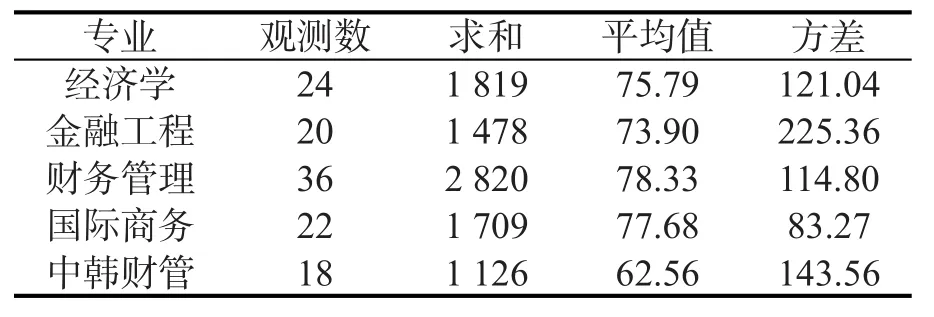
表1 5个专业统计学分数的描述统计

依据假设检验，原假设H0：专业对于统计学成绩没有显著影响；备择假设H1：专业对于统计学成绩有显著影响。由统计量F=6.34，又F0.05(4,15)=2.45，F＞F0.05(4,15)，故拒绝原假设H0，表明专业对于统计学成绩有显著性影响，这和实际是相符的，究其原因可能与统计学的学习需要扎实的数学基础有关。

方差分析不仅可以用于处理分类型变量，而且还可以处理数值型变量的问题，是一种有效的检验变量之间是否存在因果关系的统计方法。下面通过一个例子展示方差分析法在回归分析的应用。

案例2 K.pearson收集了大量有关父亲身高和儿子身高的数据（表2），试求儿子身高y关于父亲身高x的回归方程[8-9]。

表2 父亲身高和儿子身高列表（单位：cm）

解在求解回归方程之前，首先需要检验父亲的身高是否对儿子身高有显著影响，这正是方差分析要解决的问题。然而，不同于上一个例子，这个例子的自变量是数值型变量。按照方差分析步骤，首先计算总变动：其次，计算组间平方和、组内平方和分别为SSY=进而可得组间均方和、组内均方和分别为MSY=SSY/dfY=1152766.92/9=128085.21，MSe=SSe/dfe=11331.40/20=566.57。最后，构造F-检验统计量F=MSY/MSe=128085.21/566.57=226.07。在置信水平α=0.05下，查表可得F0.05(9,20)=2.39。显然F＞F0.05(9,20)，表明父亲身高与儿子身高存在因果关系。

方差分析仅仅表明父亲的身高对儿子的身高有较强的因果关系，但不能给出具体的数量关系式。为了进一步量化这种因果关系，需要利用回归分析计算相应的函数关系。由于在每个观测点处有多个观测值，因此选取这些观测值的平均值yi作为对应观测点处的回归值，通过取平均值的手段还可以在一定程度上过滤数据中的噪声。

假设这种函数关系是线性函数，即f(x)=ax+b,a,b∈R。由普通最小二乘估计式则有：

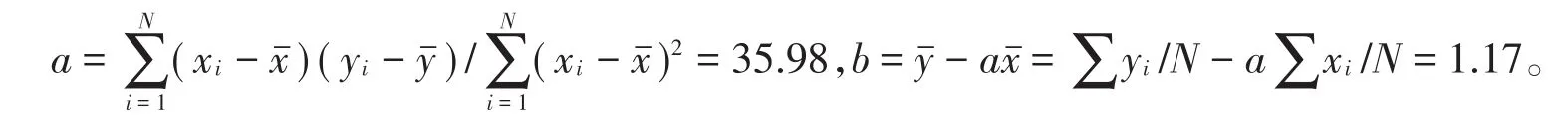
这里，xi，yi为样本观测值，xˉ为样本观测值的均值，yˉ为所有样本观测值的均值。最后，可得回归方程为f(x)=35.98x+1.17。

3 结束语

文章探讨了如何在教学过程中采用启发式教学方法向学生讲授方差分析，从而使学生理解、掌握和应用方差分析。通过本次教学探讨，学生明确了方差分析的概念、基本思想和计算步骤，为以后熟练应用方差分析打下了坚实的基础。文章最后通过案例2讲解方差分析在回归分析中的应用，这将更有助于学生理解方差分析与回归分析的关系，为以后学习回归分析作了铺垫。