关于修复代数几何码的一个注记

陈雯雯，胡万宝，崔良武，胡 帅

（安庆师范大学数学与计算科学学院，安徽安庆246133）

分布式存储系统是指运用一定的技术手段，将原始数据分别存储在相互独立的若干台设备(节点)上，常采用不同程度的冗余校验来提高系统的稳定性，现已被广泛应用。在采用编码技术的分布式存储系统中，常需要进行节点修复。节点修复问题[1]是指当存储了编码数据的节点发生失效，为了维持系统的稳定性，需要再生出失效的数据并将它存储在新的节点上替代失效节点。文献研究表明，如果系统仅有一个节点失效，采用纠删码技术恢复数据时，必须要先恢复出完整的原始数据，这样势必会增加修复带宽，降低修复效率。为了减小修复带宽，提高修复效率，人们对传统纠删码进行了一定的改造和优化，定义了若干种再生码[2]解决节点修复问题。本文提出一种利用再生码解决节点修复问题的修复方案。下面先介绍一般代数几何码的修复算法。

1 代数几何码的修复算法

有限域Fp的特征可以为偶素数，也可以为奇素数。关于代数函数域和代数几何码的相关概念综述可参考文献[3-4]。下面先给出方案中需要用到的迹对偶基[5]和对偶码[6]的定义。

定义1[5]设Fp是一个有限域，Fq是Fp的域扩张。选取Fq在Fp上的两组基和，若当1≤i,j≤t时，存在一个Fq到Fp上的迹映射Tr使得则称这两组基为迹对偶基。

定义2[6]设是一个一般线性码，对于一个集合，若对任意的c=满足称W为C的对偶码，通常记为C⊥。

1.1 一般线性码的修复方案

设Fq在Fp上的扩张次数为t，对于一般线性码将中的每一个向量看成是由一个函数赋值生成的。例如，若赋值点集合对于任意c∈ C，存在一个函数f使得因此，C可视为由若干个不同的函数f生成的一个Fqn的子空间。也就是说，将函数f看作一条信息，每一个赋值点对应一个存储信息的节点，相对应的向量c=是一个码字，c中的每个分量是Fq中的一个符号。

线性码的修复实际上是由一组t个函数决定的[8]，具体描述：假设一个码字，若第i个节点失效，即数据丢失，修复则需要找到一组函数，这里( i, u)中的i是指第i个节点失效，在所做的单个节点失效问题中，是固定的且满足：对于每并且使得，由(1)式可得

因为迹函数是线性映射，所以可得t个等式

为了恢复f(αi)，需要充分检索的信息去计算(2)式。

1.2 RS码的修复方案

RS码是一种特殊的线性码，生成它的一组函数f均为低次多项式，先给出RS码的定义。

定义3[8]设Fq是一个有限域，Fq[ ]x是Fq上的一个多项式环，A是一个赋值点集合A=一个Fq上的k维RS码RS被定义为

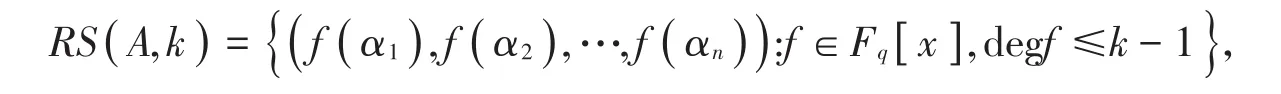
对于一个RS(A ,k)码来说，假设失效节点存储的信息是，则需要找到一组函数h(i,u)使得其生成的对偶码在Venkatesan等所研究的RS码的精确修复方案中[8]，令函数其中Tr是F到F上的迹函数，α是在失效节点的赋值点，则qpi满足和对于所有

1.3 代数几何码的修复方案

代数几何码是RS码的一种自然推广，所以代数几何码的修复算法和RS码的修复算法类似。对于一个代数几何码，由RS码的修复方案可知，在代数几何码修复方案中，假设所在节点发生失效，信息丢失，要想恢复的信息，关键是要找到一个函数h(i,u)使得满足bi(i)=t和对于所有

设Fp是一个有限域，Fq是Fp的一个域扩张，且其扩张次数为t，选定Fq在Fp上的一组基及对偶基由(1)式可知，对于一个代数几何码来说，失效节点信息为

引理1[7]设m，r，d都是正整数，且满足假设对于某个固定的存在一个函数使得，则是一个带宽b=的再生码，其中

基于Fp的特征是任意值的前提，下面进行带宽的计算。设V是Fq上的子空间，其在Fp上的维数为l。定义一个p-加性多项是Fq到Fp上的Fp-线性映射，由有限域知识可知，显然所以根据同态定理

定理1 设Fp是一个特征为任意素数的有限域，Fq是Fp的一个域扩张，且其扩张次数为t，F是Fq上亏格为g的函数域，是F的n+1个不同的有理位若，则是一个带宽为的再生码。

2 由Hermitian码得到的再生码

下面将给出一个Hermitian码的例子，并对比RS码和Hermitian码在同等码长下的带宽情况。

在代数几何码中，当函数域F是一个有理函数域时，相对应的代数几何码就是一个RS码，且当码长n=q时，带宽b=( )n-1 log p。

设q=r2，Hermitian码是被定义Hermitian函数域上的一种码。在Fq上的Hermitian函数域被定义为H=Fq(x ,y)，且H满足yr+y=xr+1，H的亏格为有N=1+q3个有理位，其中P∞是x和y唯一的共同极点，其余r3个有理位恰好由满足集合的r3对给出。对于设D是由Hermitian函数域H上除了P∞以外的所有有理位构成的集合，则定义Cm:=CL( )mP∞,D ，称码。

定义有理位Pα,β是由满足的有理点对应给出的。设D是由Hermitian函数域H上除了P∞以外的所有有理位构成的集合。对于每个α∈Fq，主除子和

综上，两个码在相同码长的情况下有着相同的码率和修复带宽，但是RS码定义在F729上，即每个符号存储量为log 729，而Hermitian码定义在一个更小的域F81上，每个符号存储量为log 81，也就是说Her-mitian码在数据存储上用更小的空间达到同RS码同样的效果。

3 结束语