函数点缺陷对光子晶体带隙结构的调制

张晓茹，张沥元，张 鑫，杜佳乐，苏靖淇，韩雨欣，吴向尧，刘晓静

（吉林师范大学物理学院，吉林四平136000）

1987年Yablonovitch和John分别独立提出光子晶体的概念[1-2]。光子晶体由两种或两种以上不同介电常数的材料构成，其重要特征为光子带隙、缺陷态、光局域化等[3-7]。利用这些特点，可以用来制造一些全新的高性能设备，如高效的半导体激光器、发光二极管、光学滤波器、波导、光学衰减器以及光学放大器[8-11]等。光子晶体具有周期性，因此完整光子晶体带隙结构中会出现一条很宽的禁带，当引入缺陷来破坏光子晶体的周期结构时，原来处在禁带中的光频率与束缚态的频率一致时，就会发生谐振，使原本被禁止的光子在禁带中传播，并在缺陷处形成一个量子化束缚态，形成缺陷模。近年来，广大学者研究了介质柱介电常数为常数的点缺陷对光子晶体带隙结构的影响，并为光学器件的设计提供了很好的思路[12-14]。

本课题组进一步研究当介质柱的介电常数为函数形式时，函数系数k的改变对光子晶体带隙结构的调节作用。文献[15-18]提出了二维函数光子晶体的概念，并研究了二维函数光子晶体中TE和TM波的带隙结构及Dirac点分布。二维函数光子晶体不同于二维常规光子晶体，其介质柱折射率是随空间位置分布的函数，可通过对介质柱施加外电场、光场来改变其折射率，即通过电光效应和Kerr效应使介质柱折射率成为空间位置的分布函数。在一阶电光效应中，点缺陷的介质柱介电常数函数形式为εr=n20+2αE,可以通过法拉第电磁感应定律得到外加电场为沿介质柱半径r线性分布的函数E=E0r+d，则介电常数可写为εr=2αE0r+n20+2αd=kr+b，其中k=2αE0，b=n20+2αd，E0为电场幅值，α为电光效应系数，d为参数，b为可调参数（无量纲），k为函数系数（单位为m-1），此时介电常数为沿半径r线性分布的函数。当函数系数k=0时，介质柱的介电常数为常数；当k≠0时，介质柱的介电常数为沿半径r线性分布的函数。可见，通过电光效应可使介质柱介电常数成为空间坐标函数，即点缺陷介质柱的介电常数为函数形是可以实现的。

本文在研究二维光子晶体中加入两个函数点缺陷时，点缺陷介质柱介电常数函数形式为εr(r)=k r+b，其中可调参数k的变化可通过电光效应实现，通过调节函数点缺陷的介质柱介电常数参数就可实现光子晶体带隙结构的调制。

1 二维函数光子晶体介电常数的傅里叶变换

文献[15-16]给出了二维函数光子晶体介电常数的傅里叶变换，介质柱的介电常数为

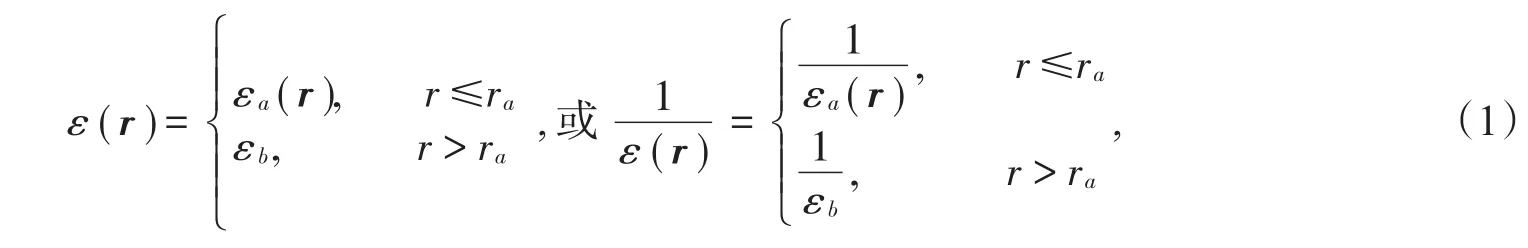
（1）式可以写为

其中

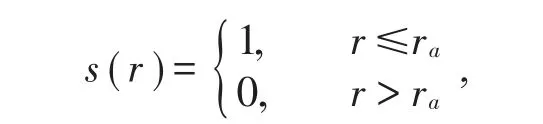
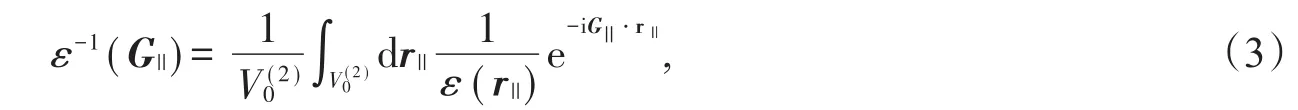
其中G||=m1b1+m2b2，r||=xi+yj，V(2)0为二维空间单原胞体积。

将（2）式代入（3）式得

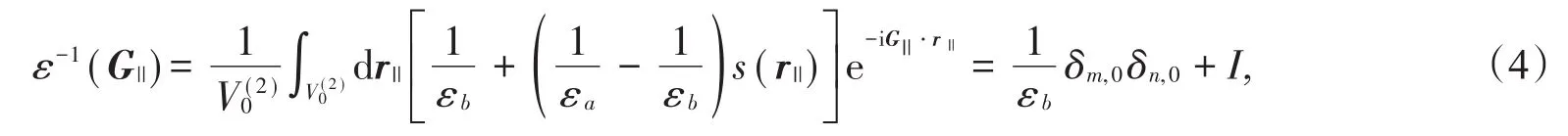
其中

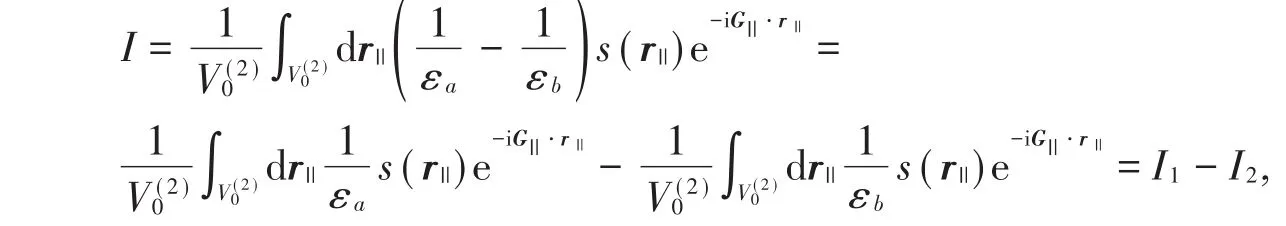
有

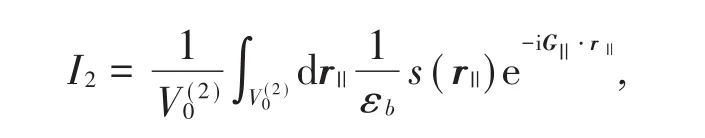
有|r|||=r||=r，|G|||=G||，dr||=ds=rdrdθ，θ为r||和G||的夹角。通过计算可知

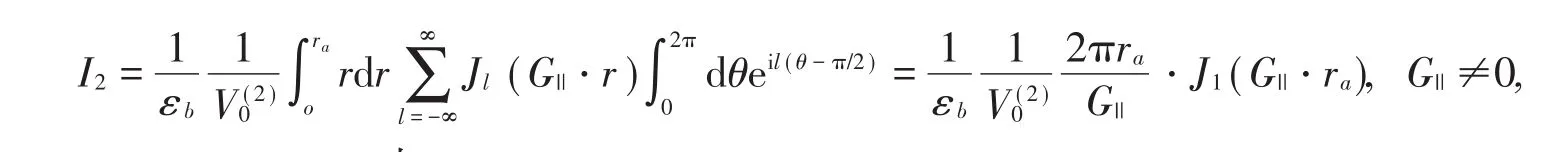
当G||→0 (m→0,n→0)时，

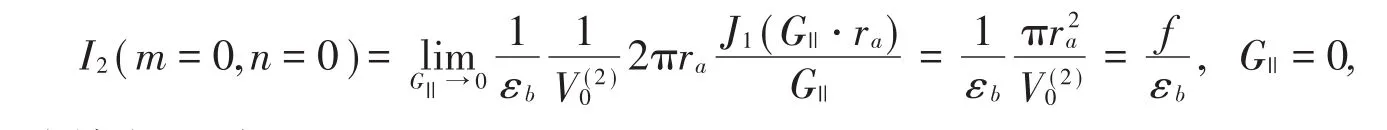
其中，f=πr2a/V(2)0为填充比，有

在方程（5）中，考虑εa(r,θ)= εa(r)，当G||=0时，则有

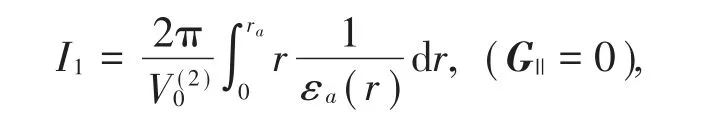
将I1，I2,和I代入（4）式可得

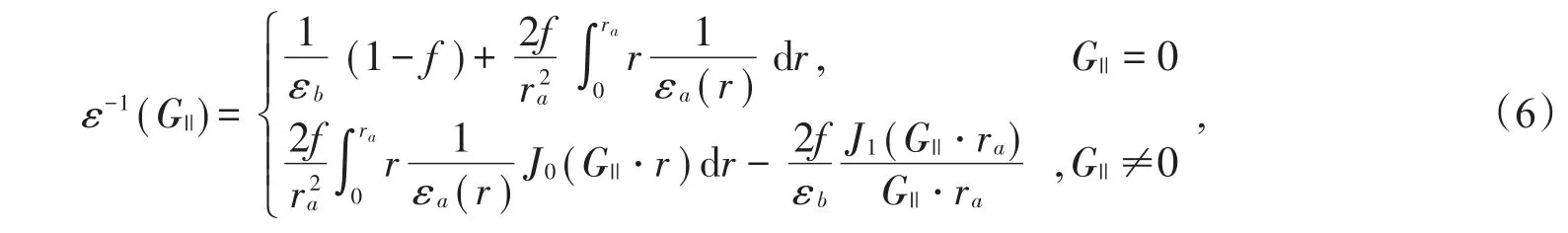
其中εa(r)= εa，εa为常数，则（6）式可以写为

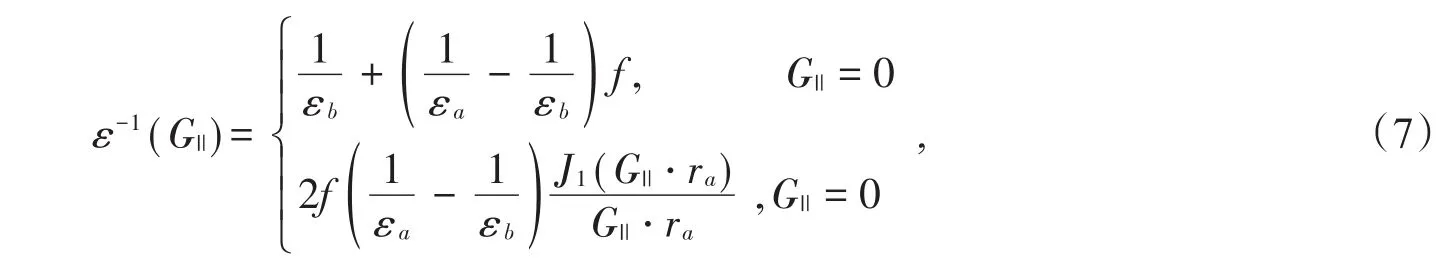
（7）式是二维常规光子晶体介电常数的傅里叶变换，可见二维常规光子晶体是二维函数光子晶体的一种特殊情况。通过平面波展开法，给出了TE波的特征方程为

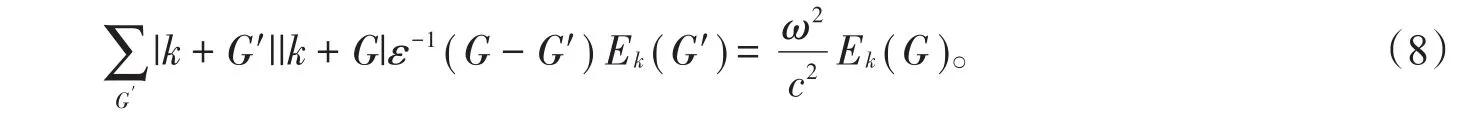
将（7）式代入（8）式可以得到二维函数光子晶体的带隙结构。

2 数值分析

根据上述理论计算和COMSOL仿真软件模拟二维光子晶体带隙结构和本征场分布。本文中，我们研究介质柱按正方形结构周期性排列在空气中的二维光子晶体，当加两个函数点缺陷时，通过改变点缺陷介质柱介电常数的参数k的数值，研究其对带隙结构的影响，并给出含缺陷的本征场在Ez方向的本征场分布。图1为含缺陷的正方结构二维光子晶体结构图，白色圆圈为介质柱，其介质柱介电常数为常数，蓝色两个圆圈为两个点缺陷，其介质柱介电常数为函数，其函数形式为εr=kr+b（0≤ra≤0.5a），ra为介质柱的半径，晶格常数a=10-7m。在光子晶体中选取7×7超原胞结构，如图中虚线矩形框内所示。

图1 含缺陷的正方结构二维光子晶体结构图

首先，通过COMSOL仿真软件模拟计算二维完整结构光子晶体带隙结构，其中，介质柱的εr=9，ra=0.3a，带隙结构如图2（a）所示。由图2（a）可看出，在频率0.26～0.34内出现一条很宽的禁带。图2（b）中阴影部分是由3个高对称点Γ、X、M所定义的简约布里渊区，其坐标分别为Γ=2π/a[0,0]，X=2π/a[0.5,0]，Γ =2π/a[0.5,0.5]。

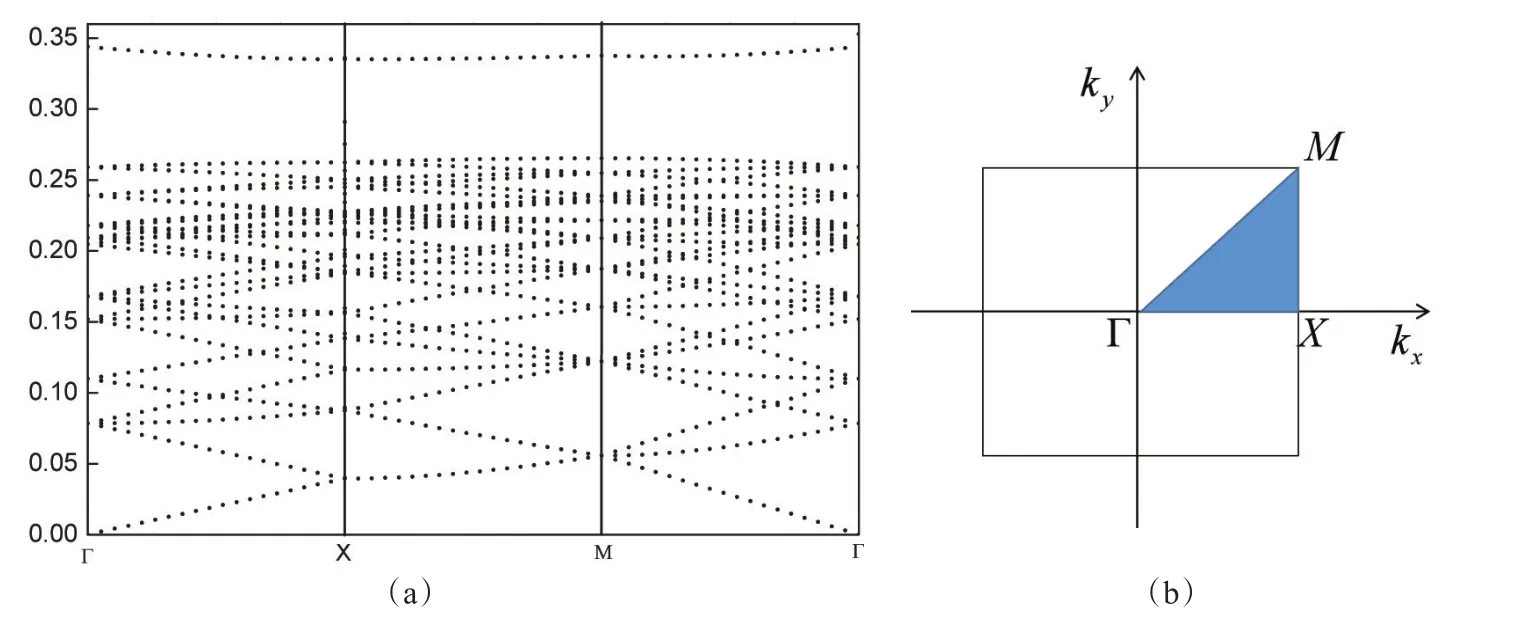
图2 （a）完整正方结构二维光子晶体的带隙结构；（b）正方结构二维光子晶体第一布里渊区的扩展图

为了破坏完整光子晶体的周期性得到禁带中某一频率的光，我们引入点缺陷。在二维函数光子晶体[15-18]相关研究的基础上，为了进一步简化光子晶体的制作过程，周围光子晶体保持为常规不变，缺陷处介质柱介电常数为空间坐标分布的函数，进一步研究点缺陷介质柱介电常数中可调参数k的变化对光子晶体带隙结构的调节作用。图3为正方结构含两个点缺陷的二维光子晶体的带隙结构和本征场分布，其中，介质柱半径ra=0.3a保持不变，可调参数k=7.8×107m-1，参数b=9，即相对介电常数εr=7.8×107r+9。

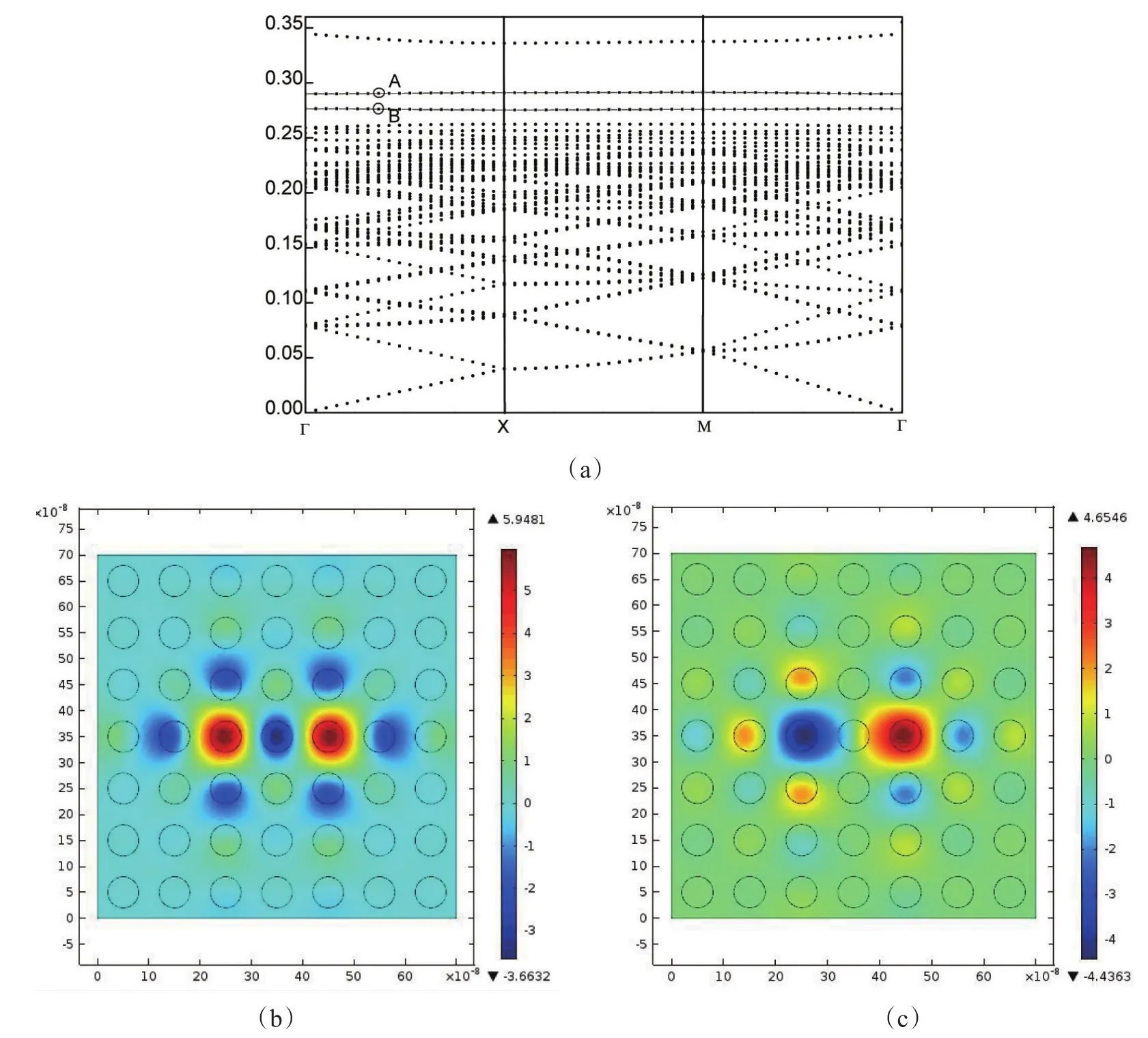
图3 （a）含缺陷光子晶体带隙结构图（k=7.8×107m-1）；（b）A点对应的本征场图；（c）B点对应的本征场

在图3（a）中，归一化频率为0.26～0.34中出现了两条缺陷模。在两条缺陷模上分别取点A坐标为（0.315 8，0.290 2）和点B坐标为（0.315 8，0.276 2），对应归一化频率在Ez方向的本征场分别为图3（b）、（c），右侧彩虹条表示场强的强弱，由上至下场强呈递减趋势。由图3（b）知，在两个缺陷位置电场强度很强，呈现偶对称形式分布，在远离缺陷位置电场强度变弱。当光子晶体周期结构被破坏，光子被局限在缺陷处时，能量不断聚集，因此缺陷处场强越来越大，远离缺陷处，场强越来越小。在图3（c）中，右侧缺陷模处电场强度很强，左侧缺陷处电场强度很弱，呈现奇对称分布，此时光的能量可以集中分布在右侧缺陷处，而左侧电场强度很弱。

在图4中，介质柱半径ra和参数b不变，可调参数k=1.58×108m-1，即点缺陷介质柱的相对介电常数εr=1.58× 108r+9，其对应的带隙结构和本征场分布对应于图4（a）和4（b）。在图4（a）中，归一化频率0.26～0.34中出现了一条缺陷模，相比于图3，缺陷模的位置红移，且模数减少。在缺陷模上取点A坐标为(0.315 8，0.273 3)，对应归一化频率在Ez方向的本征场为图3（b），在两个缺陷位置电场强度很强，呈现偶对称形式分布，在远离缺陷位置电场强度变弱。

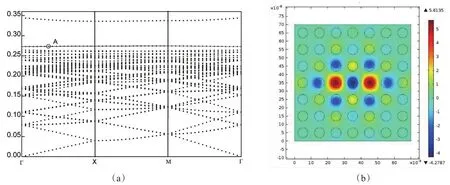
图4 （a）含缺陷光子晶体带隙结构图（k=1.58×108m-1）；（b）A点对应的本征场图

在图5中，介质柱半径ra和参数b不变，可调参数k=3.08×108m-1，即点缺陷介质柱的相对介电常数为εr=3.08× 108r+9，其对应的带隙结构为图5（a）。在图5（a）中，在归一化频率为0.26～0.3禁带中，缺陷模消失。缺陷模消失与图2所示的完整结构光子晶体带隙结构相同，即通过调节点缺陷介质柱介电常数中可调参数k可得到与完整光子晶体相同的带隙结构。

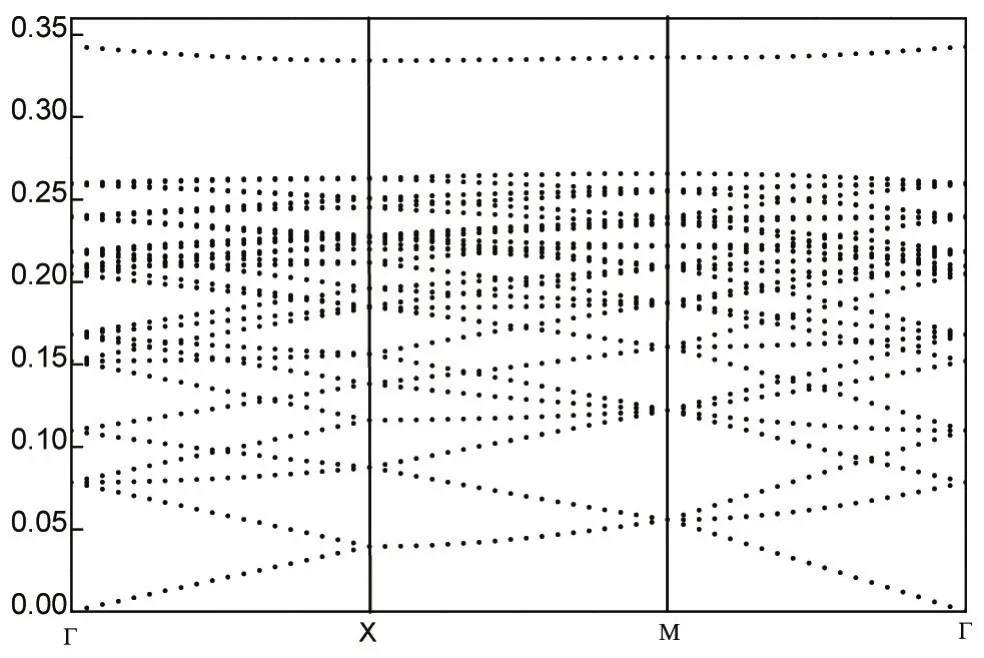
图5 含两个点缺陷的二维光子晶体的带隙结构（k=30.8×107m-1）

比较图3～5可知，当点缺陷介质柱介电常数中可调参数k增大时，缺陷模的数目减小，位置红移。可调参数k的变化，通过改变外加电场的大小和分布形式来实现，即可以通过改变外加电场的方式，方便地调节二维光子晶体的带隙结构，控制缺陷模的数量和位置，从而得到所需的带隙结构。

3 结论

综上所述，通过理论推导介质柱介电常数为空间坐标函数形式的Fourier积分解析表达式，用COMSOL仿真软件模拟得到二维光子晶体的带隙结构和电场分布。结果表明：当点缺陷介质柱介电常数中可调参数k增大时，缺陷模的数目减小，位置红移，从而可以通过改变点缺陷介质柱介电常数中可调参数k的值，实现二维光子晶体的带隙结构的调制。可调参数k的变化，可依据电光效应，通过改变外加电场的大小和分布形式来实现。由于点缺陷介质柱的介电常数的函数系数可调节，其得到的带隙结构也可调节，因此可以得到所需要的带隙结构。这为光学器件的设计提供了理论基础和新的设计思路。相比于常规光子晶体，不需要重新更换介质柱，这也会节省大量的材料成本。