陶瓷辊棒内外径之比对其抗弯性影响的研究

游越，冯青，陆琳，宫小龙

（景德镇陶瓷大学，景德镇市，333000）

0 引 言

辊棒作为辊道窑传动装置中承载与传送制品的核心部件，对其抗弯性能有较高的要求。辊棒在承重弯曲时所受最大弯曲正应力大小与辊棒荷重及截面尺寸相关，目前公知的辊棒截面为圆环结构，为尽可能的减小辊棒在受力弯曲时的最大的弯曲正应力，辊棒截面应选取合理的截面尺寸。本文将从理论验证辊棒内外径之比对辊棒弯曲时最大弯曲正应力大小的影响，并通过计算机计算与拟合辊棒弯曲所受最大正应力与内外径比的关系，为选取合理的辊棒内外径比提供理论及参考。

1 理论基础

当辊棒承受制品压力和自身重力时会产生弹性弯曲变形，当发生弯曲后，一些层面的纵向会伸长变形，而一些层面会发生缩短变形。但在伸长层和缩短层交界处，既不发生伸长也不发生缩短的层面，称为“中性面”。中性面与辊棒横截面的交线，称为该截面的“中性轴”，如图1 所示。距离中性面越近的层面变形程度越小，反之越大。根据弹性范围内的应力—应变关系即胡克定律可知：应力与应变呈正相关。因此越接近中性面的层面受到的弯曲正应力越小，反之越大。

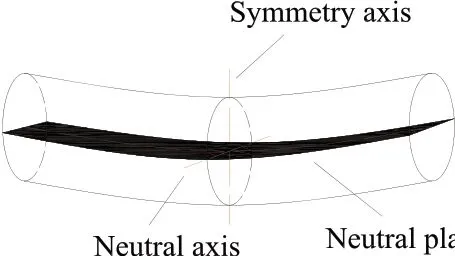
图1 辊棒变形示意图

辊棒在弯曲时，同一截面上的弯曲正应力沿着弹性变形应变方向呈线性分布，如图2 所示。截面上任意点弯曲正应力公式如下：

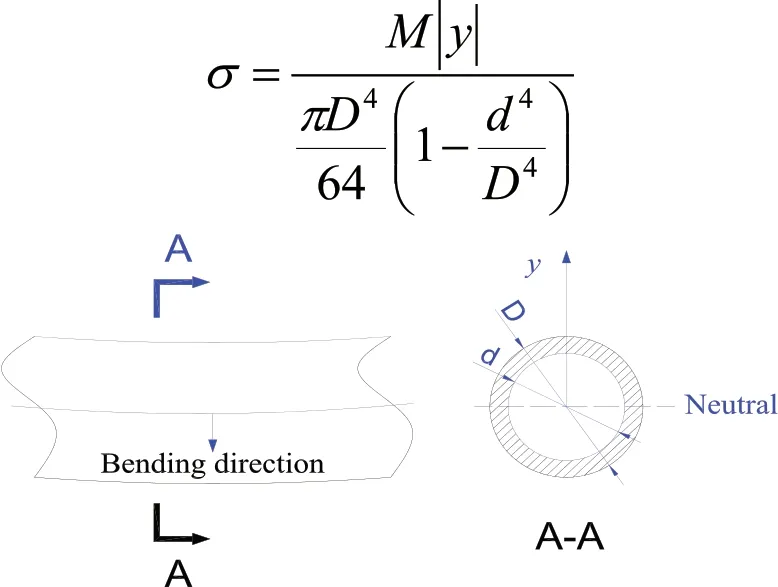
图2 辊棒截面弯曲正应力分布

2 计算与验证

当辊棒体积一定时，载荷与辊棒质量不变，因此辊棒所受弯矩M 不变。设辊棒截面面积为单位“1”，此时辊棒内径为

根据弯曲最大正应力公式：

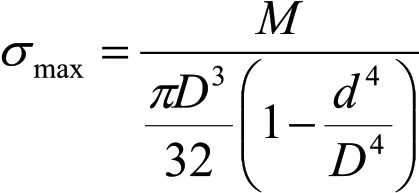
可得：

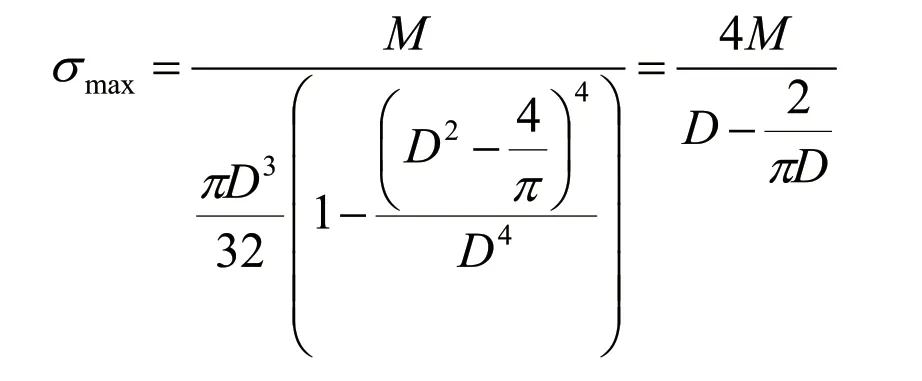
通过对σmax关于 的函数计算，可拟合辊棒体积一定时，辊棒外径与辊棒最大正应力的函数曲线，函数曲线如图3 所示。其中η 为内外径之比，σmax 是辊棒上的最大弯曲正应力，r 为最大弯曲正应力相比最大值时的减小百分比，k 是辊棒相比同体积实心辊棒外径增大百分比。

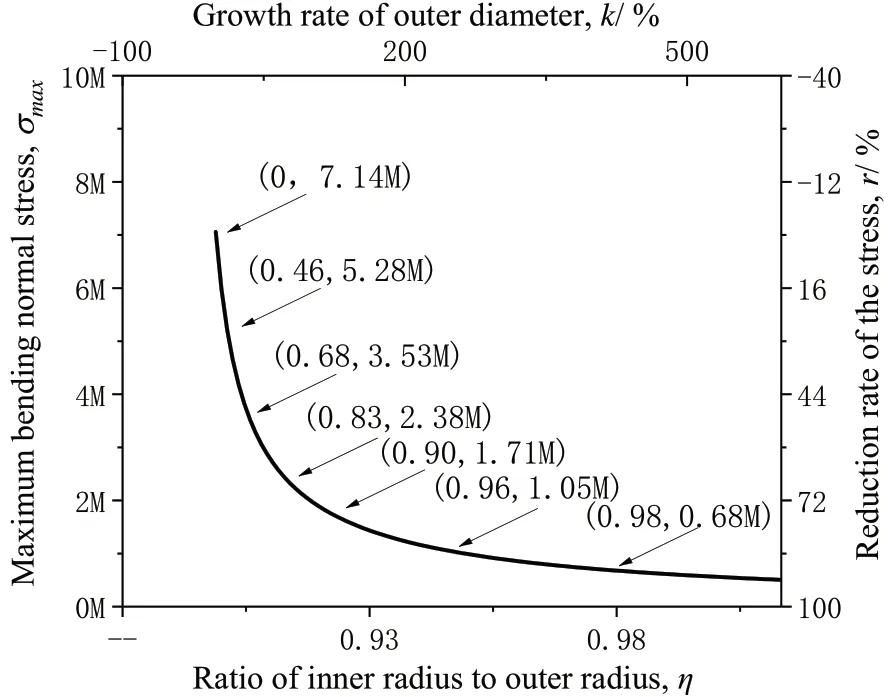
图3 最大正应力与内外径比关系图

由上图可得，在辊棒体积一定时改变辊棒截面尺寸，辊棒最大弯曲正应力变化如表1 所示：

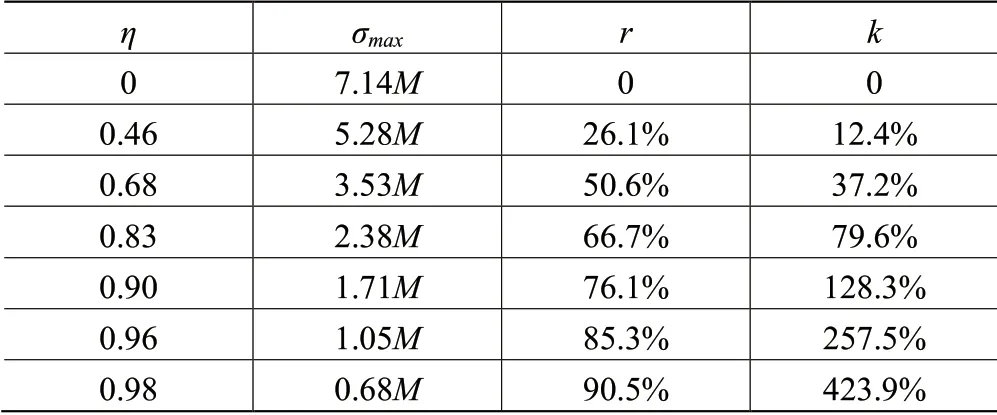
表1 内外径比与对应最大正应力

由上述图表可知，辊棒在一定体积下，内径为0，即截面为圆时，所受弯曲

正应力最大。当外径增大的同时内径也增大，辊棒壁面变薄，最大弯曲正应力逐渐减小。当增加辊棒外径，内外径之比由0 到0.83 时，最大弯曲正应力减小较快，即此阶段增大外径提高辊棒抗弯性效益较高；当内外径之比超过0.83 时，最大弯曲正应力减小速度缓慢，即此阶段增大外径提高辊棒抗弯性效益较低。通过对公式：

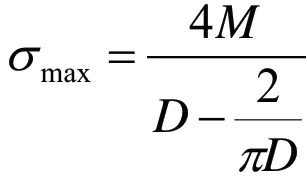
微分可得辊棒最大弯曲正应力减小率与辊棒外径的函数关系：

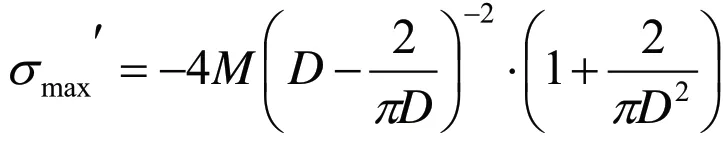
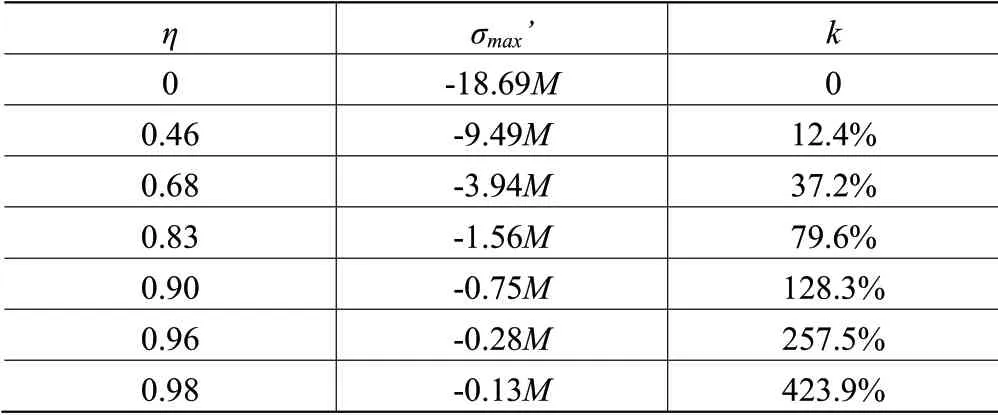
表2 内外径比与对应最大弯曲正应力变化率

综上图表可知，一定体积辊棒，随着外径增大，最大弯曲正应力减小率逐渐减小并无限接近于0。当辊棒内外径之比为0.83 时，最大弯曲正应力减小率与其最大值接近相差一个数量级。

3 结 语

1）本文通过理论及计算验证：同体积的辊棒荷重产生一定弯曲，相比空心辊棒，实心辊棒所承受的最大弯曲正应力最大。

2）对最大正应力关于外径的函数及其导函数的计算与拟合得出：同体积的辊棒荷重弯曲，外径越大，辊棒上的最大弯曲正应力越小，但随着辊棒外径的增大，增大外径减少辊棒的最大弯曲正应力的效益逐渐降低。

3）根据计算结果可得。增大内外直径比由0 到0.83时，减少最大弯曲正应力的效益较高；此后继续增大内外直径比，减少最大弯曲正应力效益较低。内外直径比为0.83 时，相比同体积实心辊棒，弯曲时所最大受弯曲正应力减小66.7%。

4）当增大内外径比过大时，减小辊棒的最大正应力的同时会导致辊棒壁厚尺寸过薄。因此选取辊棒截面尺寸时，应根据辊棒的材料属性及体积使用合适的内外直径比。