带螺旋侧板的Spar平台涡激运动数值模拟

何佳伟 ，赵伟文 ，万德成*

1上海交通大学海洋工程国家重点实验室，上海200240

2高新船舶与深海开发装备协同创新中心，上海200240

3上海交通大学船舶海洋与建筑工程学院，上海200240

0 引 言

目前，世界上常用的深水生产平台包括浮式生产储油轮（FPSO）、半潜式生产平台（Semi-sub）、Spar平台及张力腿平台（TLP）等，其中Spar平台因相对于其他深水浮式生产平台具有稳性好、运动性能更优的特点，故成为当今世界深海石油开采的有力工具。Spar平台主要有3种类型：传统型、桁架型和蜂巢型。Spar平台在来流作用下，细长的圆柱形结构部分会交替泄涡产生顺流向的拖曳力和横流向的升力，这种周期性的流体力作用在平台上，平台就会随之周期性地往复运动［1］，这种流固耦合问题称作“涡激运动”（Vortex Induced Motions，VIM）。

在单柱以及Spar平台的涡激运动发生机理、影响因素和性能预报等方面，许多学者［2-7］进行了大量的数值和实验研究。Spar平台涡激运动会导致立管疲劳和锚泊系统损伤，是影响平台和立管安全及正常作业的重要因素。因此，有必要对Spar平台的涡激运动抑制措施进行专门的研究。目前，螺旋侧板是针对柱形结构物减涡使用最多的一种装置，其主要是通过扰乱漩涡分离角度以达到消减漩涡强度的目的，最终减小涡激运动幅值。

有关抑制Spar平台涡激运动的研究，国内外不少学者开展了相关工作。成欣等［8］研究了螺旋侧板对浮式风机动态响应的影响，通过与不附加螺旋侧板情况下的动态特性参数进行对比，发现附加螺旋侧板后，浮式风机的垂荡和纵摇运动幅值与所受波浪力均得到了显著抑制；与纵荡和纵摇运动相比，垂荡运动幅值和所受波浪力均受到了较大影响；螺旋侧板对缆索张力无明显的抑制作用。张楠等［9］采用大涡模拟（LES）方法，通过对水动力系数、漩涡发放频率及尾涡形态的分析，研究了3种不同截面形状（矩形、三角形和圆形）螺旋侧板对涡激运动的影响。孙洪源等［10］研究了浮式圆柱体在均匀流下的涡激运动响应，并对其进行了水槽模型实验研究，测试了折合速度在1.3～10.2范围内的有、无螺旋侧板圆柱的运动响应。研究发现，裸圆柱在折合速度为6～8时发生了锁定现象，而增加螺旋侧板后抑制涡激运动效果显著，且无明显的锁定现象；在流固耦合作用下，涡激运动横荡频率不再符合斯特劳哈尔（Strouhal）频率变化规律。Lefevre等［5］对加装了螺旋侧板的Spar平台采用基于SA模型的分离涡方法（SA-DES）、基于剪切输运应力方程的分离涡方法（SST-DES）和改进的延时分离涡方法（IDDES）等几种湍流模型进行数值模拟，并与模型试验进行了对比，其工作对采用CFD手段进行涡激运动研究具有指导意义。Van Dijk等［11］对桁架型 Spar平台的 VIM 试验方法进行了阐述，并对有、无螺旋侧板的VIM运动情况进行了比较，结果显示螺旋侧板可以显著降低桁架型Spar平台的VIM运动幅值。

CFD方法被广泛应用于海洋工程结构物数值模拟，本文也将采用CFD方法进行研究。Spar平台的涡激运动问题在模型尺度下一般来说其雷诺数已经很大，达到10万量级，更不用说实尺度。因此，选取合适的湍流模型数值模拟Spar平台涡激运动问题就显得至关重要。从文献［12］中可以看到，对于涡激运动问题，数值模拟多采用商业软件，湍流模式也多采用模化平均的RANS方法以及模拟虽精细但耗费计算资源的LES方法。本文将采用一种混合RANS和LES的湍流模式对此问题进行一些有益探索。湍流模式选取基于剪切输运应力方程的延时分离涡（SST-DDES）方法，SST-DDES基于SST模型的分离涡方法在RANS求解区域采用未经修改的SSTk-ω模型作为控制方程，在LES求解区域采用改造后的SSTk-ω模型作为亚格子模型的控制方程。在降低计算量的同时，保证LES湍流区域的求解精度。整体求解本文将采用基于开源OpenFOAM开发的自主研制的CFD求解器naoe-FOAM-SJTU，对带螺旋侧板的Spar平台涡激运动进行数值模拟，预报Spar平台在均匀来流下的水动力学特性。同时，分析Spar平台横向和流向运动时间历程、频谱特性、锁定现象等，揭示其内在机理。

1 数值方法

1.1 运动方程

Spar平台横向和纵向的运动方程可以分别表示为以下形式：

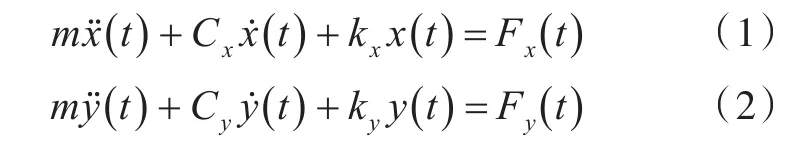
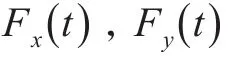
若考虑艏摇运动，则需要求解额外的艏摇运动方程：

1.2 涡激运动相关参数

涡激运动是一个典型的流固耦合问题，其影响因素比较复杂。研究涡激运动问题时，常关注如下几个关键的无因次参数。

雷诺数：

平台在来流中的无量纲折合速度：

斯特劳哈尔数：

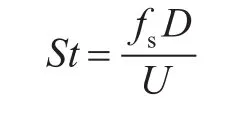
无量纲振幅比：

质量比：

式中：U为流体速度；D为特征长度（对Spar平台而言，特征长度通常取为直径）；υ为流体的运动粘度；fn为平台在静水中的横荡频率；fs为平台的泄涡频率；A为平台的横荡运动幅值；mass为平台的质量；Δ为排水量。对半潜和Spar平台来说，一般质量比mr近似为1。

1.3 动网格和水平弹簧

为了求解物体运动，计算中需要采用动网格技术。本文采用OpenFOAM中的动态变形网格技术处理Spar平台涡激运动时的网格运动，这种动态变形网格方式可保持拓扑关系不变，通过网格单元拉伸和变形来处理网格运动，网格的运动通过求解基于有限元的网格运动拉普拉斯方程得到。有关动网格方法，赵伟文等［4］采用该方法对一座Spar平台标准模型进行模拟，证明了其对于此类问题模拟的可靠性。Spar平台的系泊系统对平台起限制位移的作用。在进行平台涡激运动模型试验时，通常将其运动限制在水平面内，仅考虑3个主导运动（横荡、纵荡及艏摇）。因此，平台系泊系统以水平线性弹簧替代模拟。

2 数值计算设置

2.1 计算模型

计算模型选取 Thiagarajan等［13］于 2015年进行实验时所用的Spar平台，主要计算参数如表1所示（表中D为圆柱直径）。对该Spar平台模型进行VIM数值模拟，将平台硬舱部分简化为刚性圆柱的缩尺比模型，圆柱加装螺旋侧板，考虑侧板的涡激抑制效应。本文模拟中3块螺旋侧板相互间隔120°。

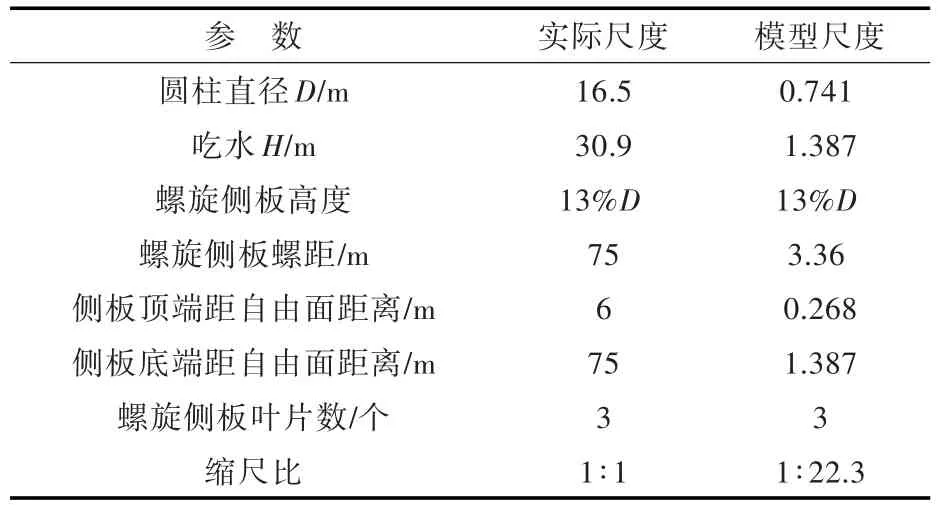
表1 Spar平台计算模型主要参数Table 1 The main parameters of Spar platform

由于在模拟过程中Spar平台会大幅度运动，所以采用自主开发求解器naoe-FOAM-SJTU中的六自由度运动模块和动网格进行计算模拟。为保证所模拟Spar平台尾涡充分发展，将平台布置到了计算域靠近入口的一侧，同时距两侧5D，以保证其不受两侧边界的影响。计算大小为：-5D＜x＜12D，-5D＜ y＜5D，-3D＜z＜0。整个计算域大小和网格划分情况如图1所示。在Spar平台周围小范围进行了加密，矩形区域大小为：-D＜x＜8D，-2D ＜y＜2D，-2D＜z＜0。网格划分工具采用Open FOAM的block Mesh和snappy Hex Mesh，脚本自动生成得到非结构网格，近壁面的网格厚度y+≈1，最终加装了螺旋侧板和无螺旋侧板的总网格量分别约为480万和400万。加装螺旋侧板后网格量稍有增加，是因为圆柱表面和侧板连接处需要加密，但算例整体网格控制在一个加密等级和量级。

2.2 网格收敛性验证

图1 计算域示意图和网格划分Fig.1 The schematic of computational domain and meshes

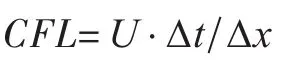
表2所示为5套网格的参数和对应的平均阻力系数计算结果。从表中可以看出，网格数量的提高对平均阻力系数值影响不大。因此，为保证计算精度并兼顾计算效率，本文使用细网格1，总网格数约480万。

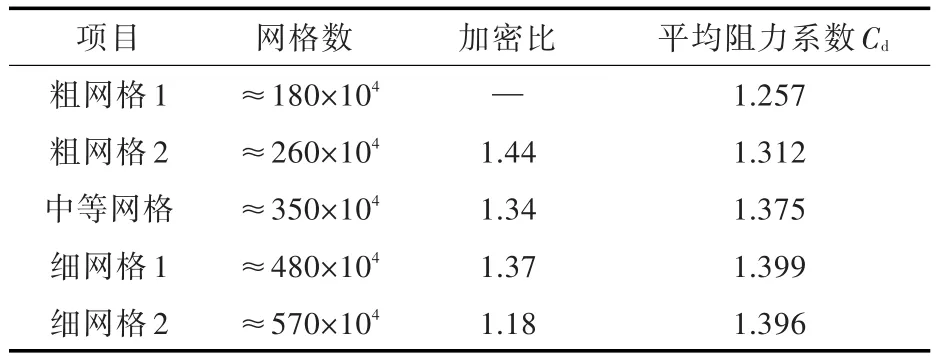
表2 5套网格的平均阻力系数计算结果Table 2 Computational results of average resistance coefficient with five sets of mesh

2.3 边界条件及数值离散

本文边界条件设置如下：速度入口、压力出口；顶部为对称边界，底部为可滑移条件；左面和右面均为可滑移条件；在模型表面，采用无滑移固壁边界条件。

求解控制方程时，采用有限体积法离散，时间项采用二阶隐式欧拉格式离散，压力速度耦合采用Open FOAM的PIMPLE算法求解。由于PIMPLE算法有允许使用大时间步长的优势，故很适合涡激运动这种计算时间长的问题。对流项采用带限制器的线性差分（Total Variation Diminishing，TVD）格式离散，扩散项采用高斯线性守恒格式离散。

2.4 分离涡模拟

分离涡模拟（DES）是目前最流行的混合RANS-LES湍流模型。DES经过了一系列的发展，最初，由Spalart等于1997年对 SA（Spalart-Allmaras）模型进行改造提出SA-DES模型，接着，Menter等也基于两方程的SST模型发展了SST-DES模型，随后，又基于改进模型应力损耗（Modeled Stress Depletion，MSD）问题在 SST-DES的基础上发展出SST-DDES模型。DES的主要思想是采用RANS模型覆盖边界层，通过减少近壁面处的边界层网格降低计算量，并在分离区域将模型转换为LES来降低整体计算成本，不过仍然提供了LES在分离区域模拟中的一些优点，可以保证模拟高雷诺数下大分离流动问题的求解精度。有关分离涡模拟的细节和验证工作，在文献［14］中已有详细介绍。本文选用SST-DDES分离涡方法进行数值模拟工作。

3 结果与分析

3.1 计算结果对比

图2所示是对带螺旋侧板的自由衰减试验，计算所得横荡自由衰减周期Tn=27.0 s，与文献［15］中计算结果25.5 s相比约相差5%，图中，纵坐标s（f）为对应横轴上一定频率的信号幅值。图3所示为不同折合速度下无量纲化横向最大响应幅值（Amax/D）与文献［16］中试验结果及文献［13］中CFD计算结果的对比。图4所示为有、无螺旋侧板圆柱的横荡时历曲线与文献［13］中CFD计算结果的对比，在Ur=6折合速度下，文献［13］中CFD计算给出的有螺旋侧板圆柱的横荡周期结果为25.7 s，本文计算结果为27.3 s，相对误差约5%。

3.2 VIM试验

选取 5个不同折合速度（Ur=6，7，8，10，12）进行VIM试验，如图5所示。

由图5可以看出，在不同折合速度下，来流速度大小的变化对平台横向和流向运动的影响很大。无论是否有螺旋侧板，随着折合速度的增大，圆柱在流向运动的响应幅值增大，而横向运动的响应幅值则未呈现此种情况。在无螺旋侧板情况下，随着折合速度的增大，光滑圆柱横向运动的响应幅值呈现出先增大后减小的情况，出现了“锁定”现象；在有螺旋侧板情况下，横向运动的响应幅值略有增加。

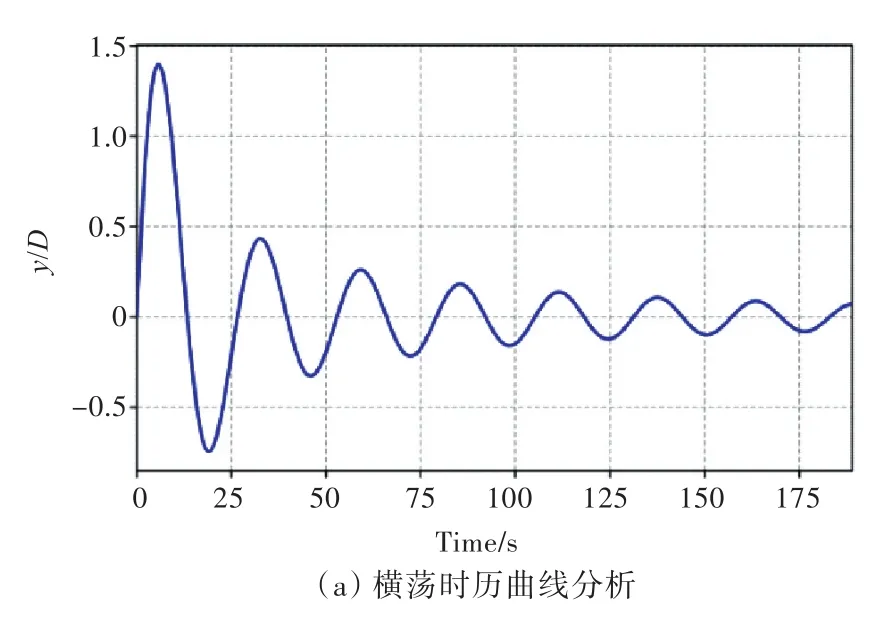
图2 自由衰减试验（带螺旋侧板）Fig.2 Free-decay tests（with helical strake）

图3 不同折合速度下无量纲化横向最大响应幅值Fig.3 Dimensionless transversal maximum response amplitude at different reduced velocities

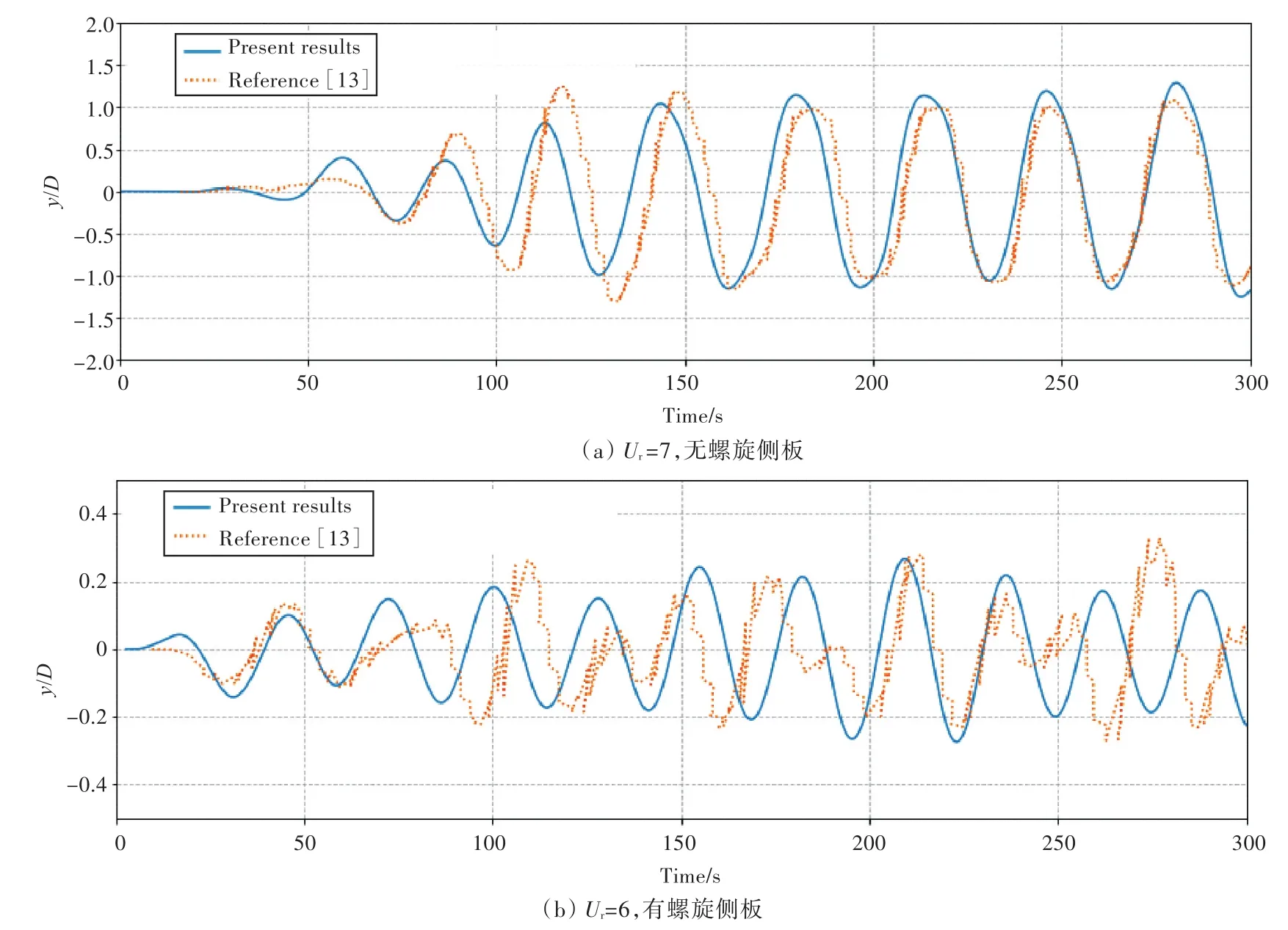
图4 横荡时历曲线与文献［13］的CFD计算结果对比Fig.4 Comparison between the time history curves of VIM sway motion and CFD computational results with the Referrence［13］

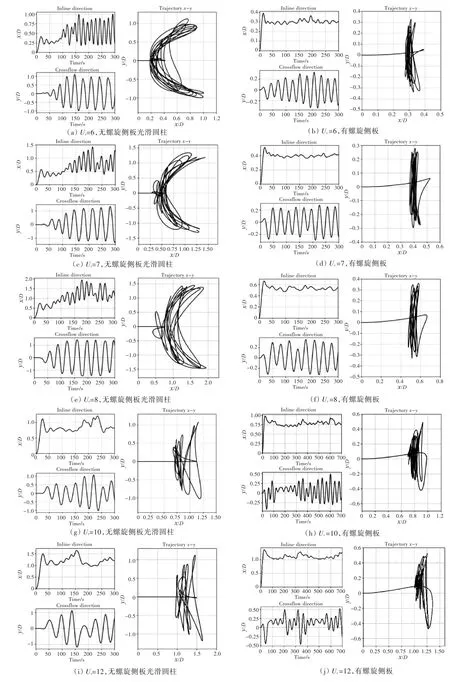
图5 不同折合速度下的横荡和纵荡时历曲线和对应运动轨迹Fig.5 Time history curves of VIM sway and surge motion and the motion trajectory at different reduced velocities

图6给出了不同折合速度下的Spar平台运动轨迹图。由Spar平台运动轨迹图可以看到，在无螺旋侧板情况下，出现了“锁定”现象，而加装螺旋侧板后未出现明显的“锁定”现象。经观察无螺旋侧板的Spar平台可以发现，当折合速度Ur=8时，Spar平台的横向运动幅值明显最大，且随着折合速度的减小（Ur=10，12），横向运动幅值明显减小，系统逐渐脱离“锁定”区域，这一过程即被称为“解锁”。锁定现象的出现，是因为横向泄涡频率接近于其横荡固有频率而产生共振现象所致。由图还可看出，是否加装螺旋侧板对Spar平台涡激运动响应的影响很大：加装螺旋侧板将极大地降低Spar平台涡激运动的横向幅值。在有螺旋侧板情况下，虽然没有发现明显的锁定现象，但有一点很明显的是，有螺旋侧板的模型横荡运动最大幅值为0.5D，相比无螺旋侧板模型的最大幅值1.5D降低了约67%；与此同时，在折合速度Ur=8、无螺旋侧板“锁定”现象发生情况下，相比有螺旋侧板，流向运动振荡（纵荡）幅值从1.25D降到了0.5D。可以看出，螺旋侧板对于抑制Spar平台的横向运动（横荡）和流向运动（纵荡）效果明显。

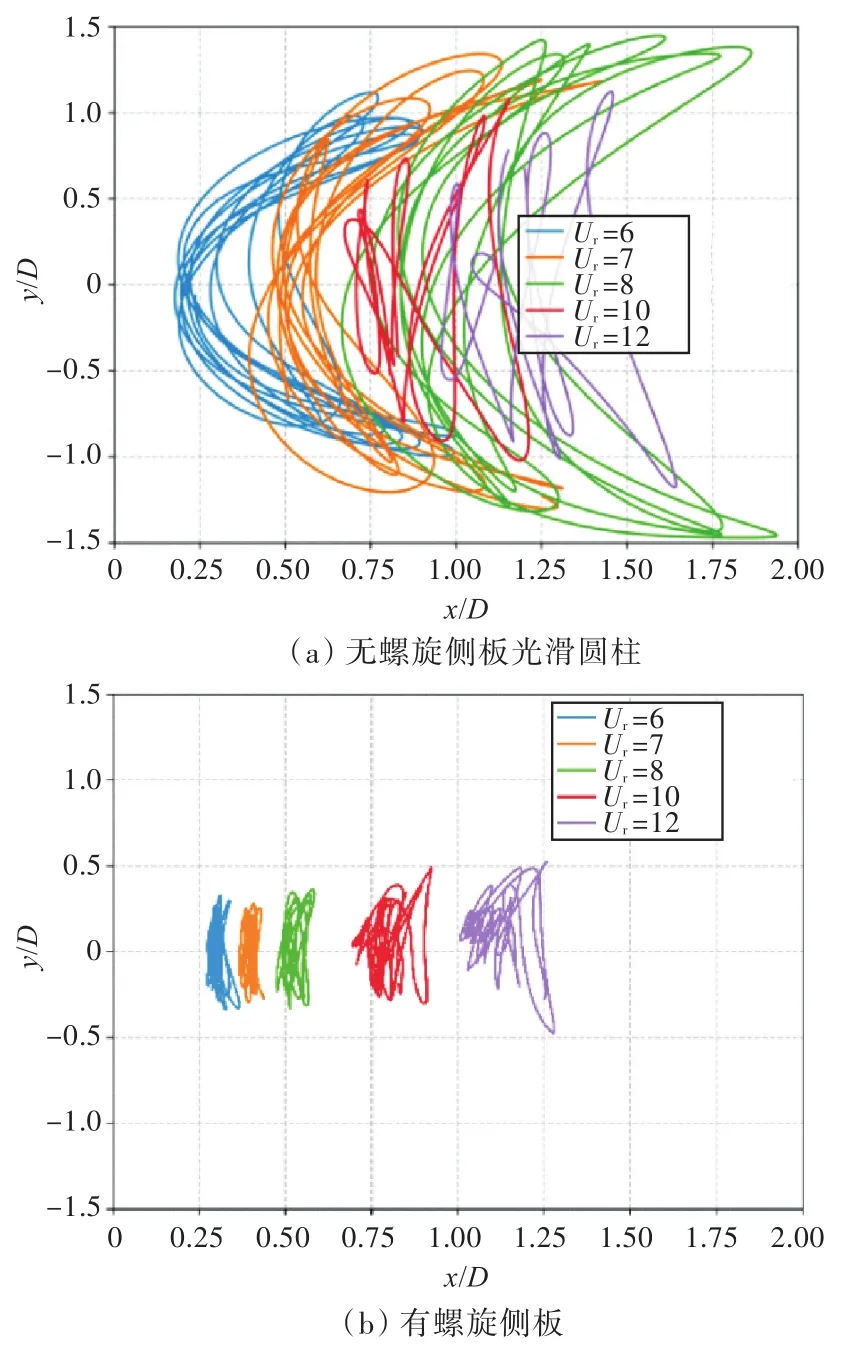
图6 不同折合速度下的Spar平台运动轨迹Fig.6 Comparison of the VIM motion trajectory of Spar platform with and without helical strakes at different reduced velocities

表3给出了有、无螺旋侧板的Spar平台涡激运动不同折合速度下的横荡运动对比。从表中可以看到，在相同折合速度下，加装螺旋侧板的Spar平台横荡周期Ty值明显小于无螺旋侧板的平台横荡周期Ty。与此同时，安装螺旋侧板后，可以看到极大地降低了其涡激运动的横向幅值。

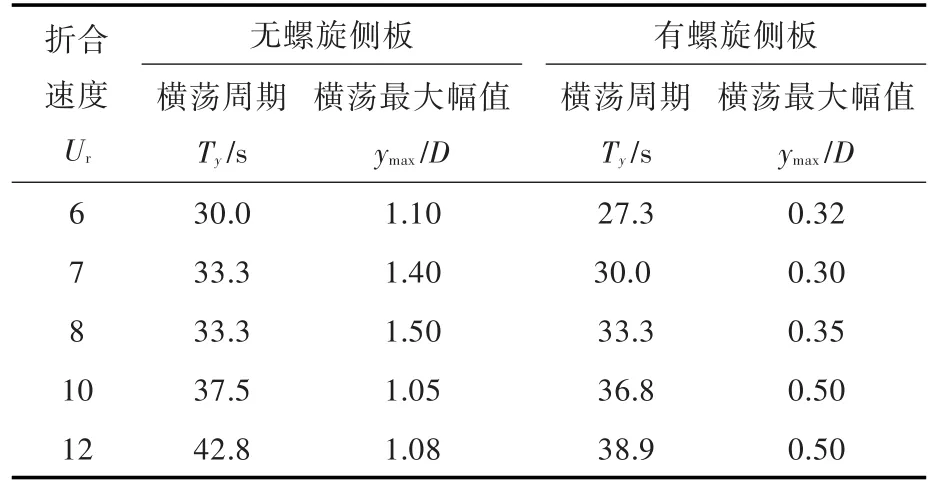
表3 有、无螺旋侧板的Spar平台涡激运动不同折合速度下横荡对比Table 3 Comparison of the simulated VIM sway motion of Spar platform with and without helical strakes at different reduced velocities

图7所示为不同折合速度下的横荡时间历程曲线傅里叶频谱分析，对其进行分析，可以得到三维流动下不同折合速度对横荡周期的影响。经对比相同折合速度下的曲线可以发现，加装螺旋侧板之后，平台横荡周期降低，因分离点转移到侧板顶端，使旋涡沿侧板进行分离，故涡旋的形态随之发生改变。同时，加装螺旋侧板后，随着来流速度的增加，从Ur=10开始，当Tn=36.8 s时，在主频附近出现了多个较明显的峰值，Ur=12时更明显，当Tn=38.9 s时，在主频附近也出现了多个峰值。可见，随着来流速度的增加，螺旋侧板的存在彻底破坏了流场尾涡的单一发放频率。

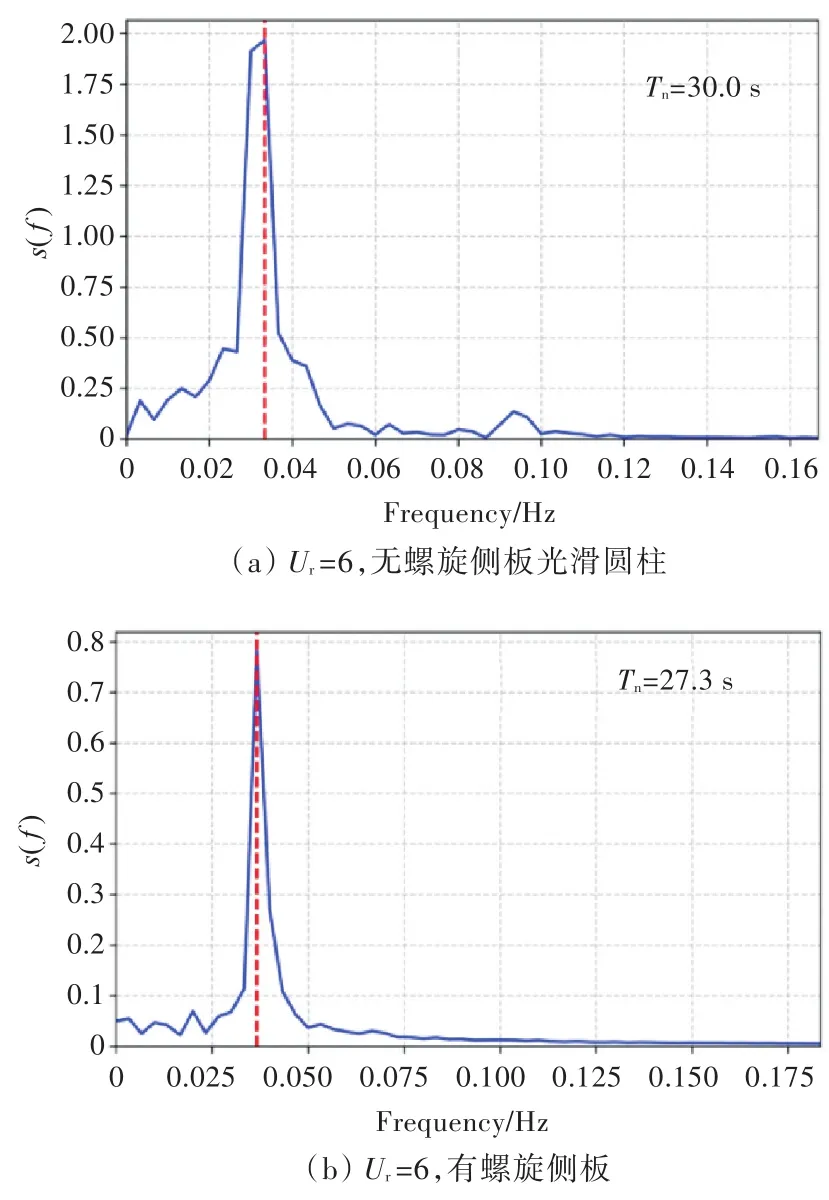
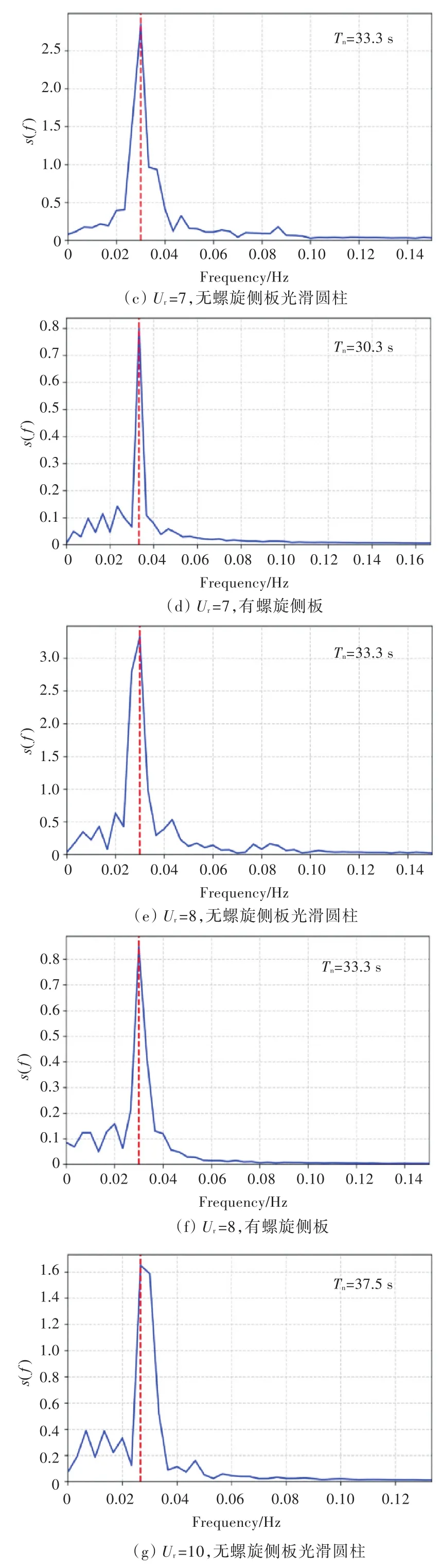
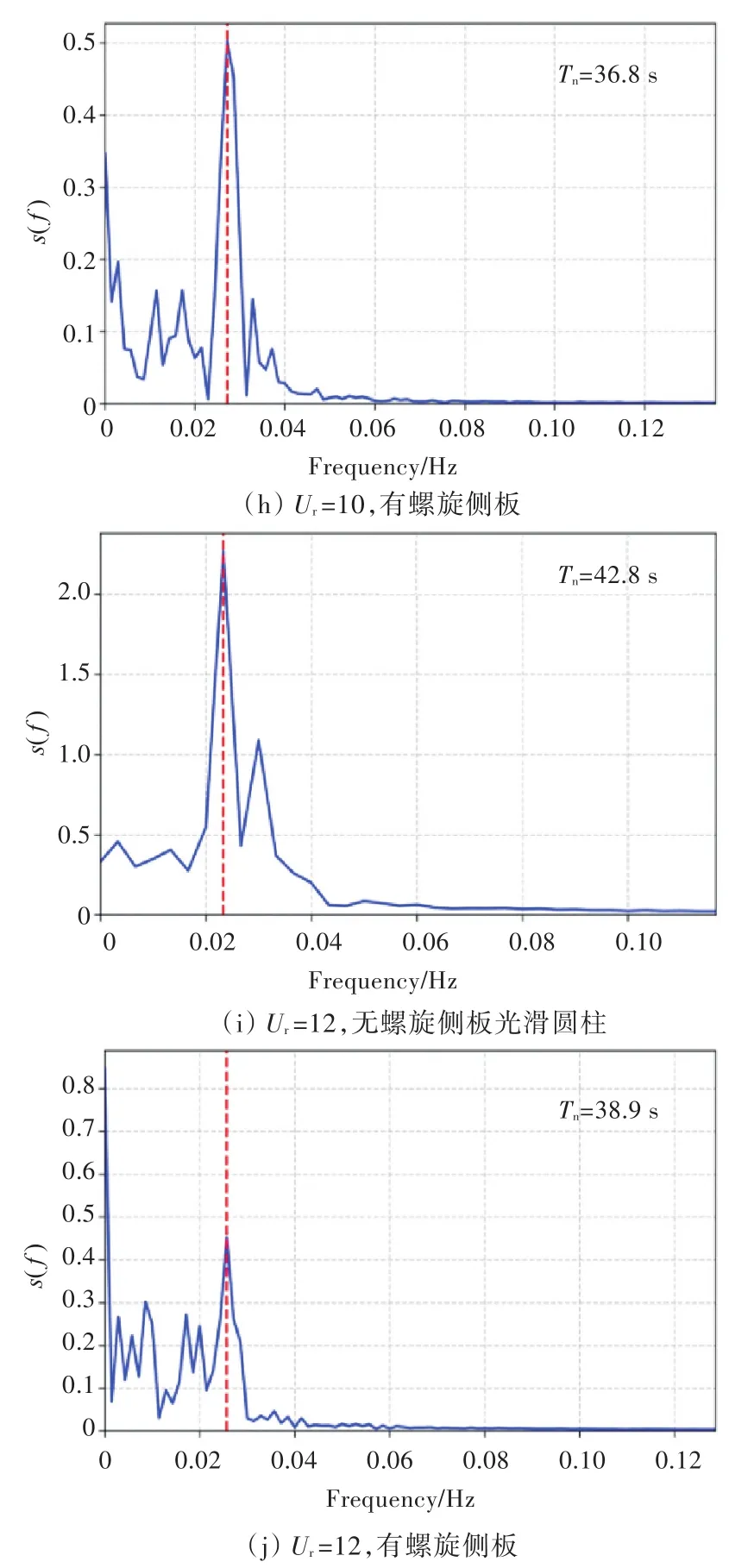
图7 不同折合速度下的横荡时间历程曲线傅里叶频谱分析Fig.7 The FFT of sway for VIM tests at different reduced velocities

图8所示为折合速度Ur=6时尾流区域瞬时三维泄涡结构图。图中，Ux/U0为无量纲化速度场x分量，其中Ux为速度场，U0为来流速度。图9为不同折合速度下水平截面漩涡分离二维涡量云图（图中 z/L=0.5，其中 L指Spar平台吃水深度）。从图可以看出，加装螺旋侧板后，流动分离都转移到侧板边缘开始，其边界层分离点变为了螺旋侧板的顶端，使得旋涡沿螺旋侧板进行分离；而无螺旋侧板光滑圆柱的流动分离则是从柱体表面开始，三维流动特性明显，破坏了涡脱落的规律性，抑制了涡激运动。图10所示为垂直截面漩涡速度云图（图中Ut/U为无量纲化后的总平均速度场）。从中可以看出，加上螺旋侧板后，自由端的高速流动区变小，在圆柱后端尾涡区，低速流动区明显比无螺旋侧板的低速流动区长且多，这也导致了运动幅值的降低，体现出螺旋侧板对涡激运动的抑制效果很好。

图8 Ur=6时尾流区域瞬时涡结构图（Q准则，Q=10）Fig.8 Vortex structure contours by Q-criterion（Q=10）in wake region at Ur=6

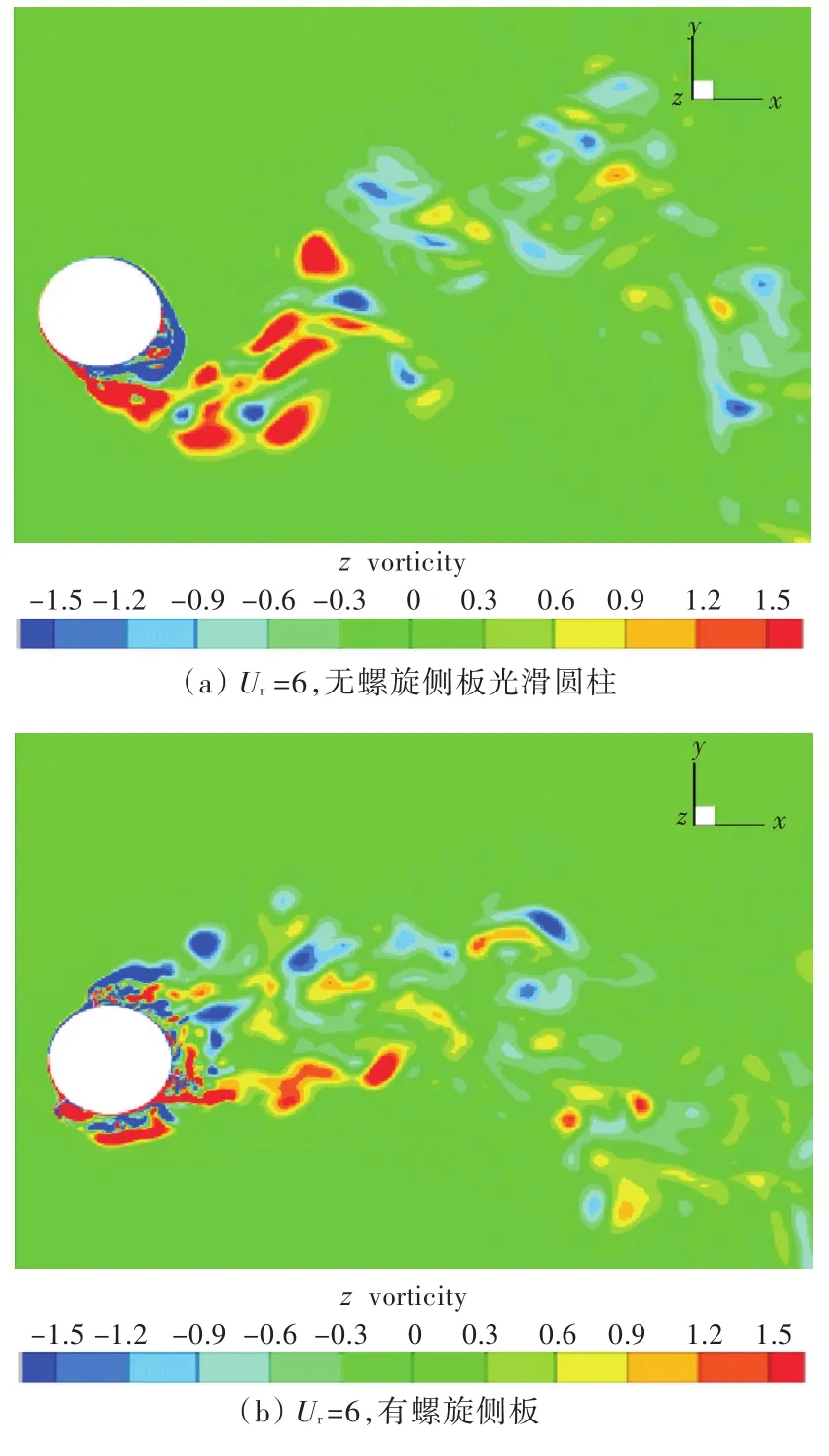
图9 不同折合速度下水平截面（z/L=0.5）漩涡分离涡量云图Fig.9 Distribution of vorticity contours on the horizontal plane（z/L=0.5）with different reduced velocities

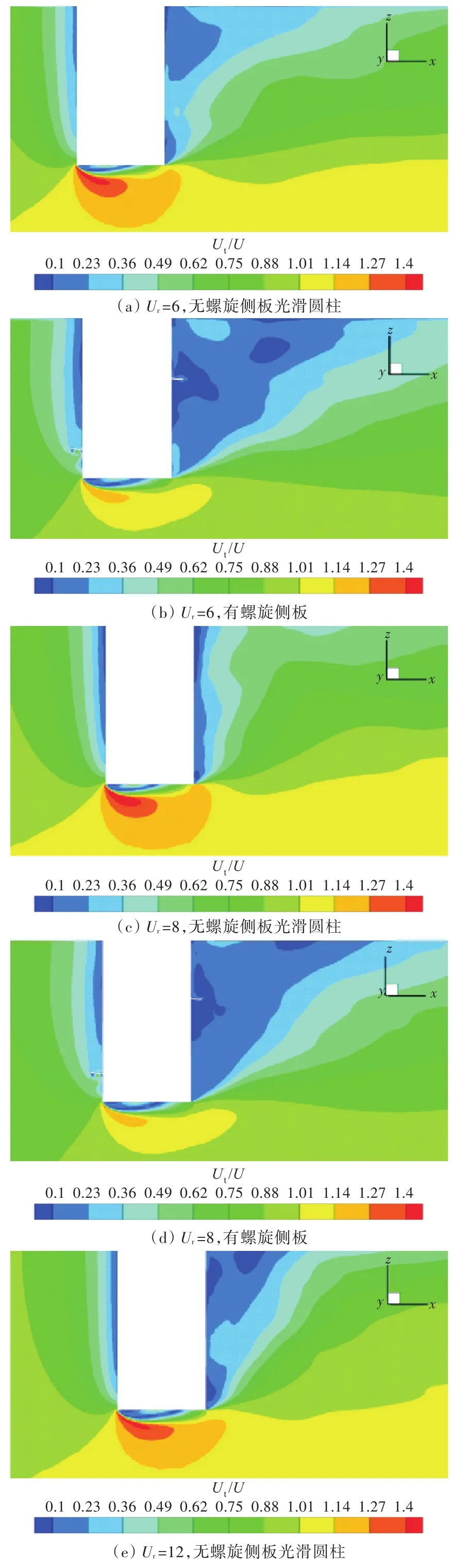
图10 不同折合速度下垂直截面漩涡速度云图Fig.10 Distribution of vorticity contours on the y=0 vertical plane with different reduced velocities

4 结 论

本文基于CFD方法，利用SST-DDES模型对无螺旋侧板光滑圆柱及加装了螺旋侧板的Spar平台进行了研究，针对有、无螺旋侧板对Spar平台涡激运动的影响进行了比较分析，得到以下主要结论：

1）在无螺旋侧板情况下观察到了锁定现象，而在有螺旋侧板的情况下，平台横向运动（横荡）响应幅值未出现明显的锁定现象。有、无螺旋侧板的Spar平台涡激运动响应有着明显的区别：加装螺旋侧板后，极大地降低了平台涡激运动的横向幅值；安装螺旋侧板后虽然未发现明显的锁定现象，但有一点很明显的是，有螺旋侧板模型的横荡响应最大幅值0.5D相比无螺旋侧板模型横荡响应最大幅值1.5D降低了约67%；同时，在折合速度Ur=8、无螺旋侧板“锁定”情况下，相比有螺旋侧板，无螺旋侧板的流向运动（纵荡）振荡幅值从1.25D降到了0.5D。可见，螺旋侧板对于抑制Spar平台的横向运动和流向运动效果明显。

2）经对比相同折合速度下的情况可以发现，与不加装螺旋侧板时相比，安装螺旋侧板后平台横荡运动周期Ty的值有所降低，分离点转移到侧板顶端，使旋涡沿侧板进行分离，涡旋的形态也随之发生改变。随着来流速度的增加，在主频附近出现了多个频率峰值，说明螺旋侧板的存在随着来流速度的增加彻底破坏了流场尾涡的单一发放频率。

3）本文的模拟和计算验证了自主开发的CFD求解器naoe-FOAM-SJTU可以用于海洋平台涡激运动问题的计算模拟。

本文采用自主开发的CFD求解器对模型尺度带螺旋侧板的Spar平台涡激运动问题进行了数值模拟，并重点考察了有、无螺旋侧板的减涡效果。尽管目前做了一些尝试，但仍有大量的研究工作要做，例如高雷诺数下的湍流模型是计算准确的一个关键因素。此外，加装螺旋侧板后来流与侧板夹角也是影响计算精度的一个因素，后续将研究加装螺旋侧板后来流角度对Spar平台涡激运动的影响。