基于遗传算法的汽车零配件生产排程问题

潘怡颖 徐嘉杰 刘大河

华南农业大学数学与信息学院，广东 广州 510642

车间生产调度问题（JSSP）是企业生产作业调度中的重大课题，汽车零配件则是汽车工业的基础，喷涂过程是汽车工业中必不可少的环节。在现有的研究车间调度的方法中，大多数是以生产周期为目标的优化问题，多为运用遗传算法、蚁群算法与粒子群算法等，通过迭代方法实现柔性作业车间调度的方案。经过对相关文献的探究，我们最终选择基于遗传算法建立的数学模型来完成多目标柔性车间排程问题。

1 问题描述

喷涂过程在传送带上完成，每个零件需要放在特定的支架上进行顺序喷涂。一圈共有303个滑橇，一个滑橇有两面，可同时喷涂，一个滑橇可看作6个相同支架，则每个滑橇放置同种零件。若前后相邻两个滑橇上的零件需要喷涂不同的面漆色，则出现了“换色”，意味着对应的喷枪需要更换涂料颜色。现需要根据指导生产量制定出未来八圈的详细喷涂排序计划，要求尽量减少换色的次数，并尽可能满足指导生产量的需求。统计出每一圈的平均换色次数及未满足生产需求的零件个数，作为判断指标。

2 问题分析

对于本题，首先要明确约束条件，并将其用数学语言进行表述，建立以颜色与零件种类为编码的遗传算法模型，然后再对模型进行优化分析，得到最优解。该问题的特点在于充分考虑生产的实际情况，用一定数量的运算解决多项式一定时间内的问题。而问题的难点在于对约束条件进行模型化处理。

3 基于遗传算法的调度优化

3.1 约束规则

换色顺序规则：任意红色和任意蓝色后面不能接任何白色；极地白后不能安排任意黑色；钻石白前必须是极地白。

零件摆放规则：（门槛B），（门槛C），（门槛A、门槛D、后保A、门槛装饰条A），3个括号对应三个项目，不同项目的任意两个产品的滑橇不能安排在一起；门槛B、门槛C不能与所有类型的雷达支架安排在一起喷涂。

3.2 模型思路

遗传算法（genetic algorithm, GA）是基于自然选择和基因遗传学原理的一种群体寻优的搜索算法，特别适用于处理传统搜索方法难以解决的复杂和非线性问题，其中就包括生产调度问题，且能为调度解提供很好的鲁棒性。

我们基于遗传算法框架，根据问题描述，进行了模型优化：把目标函数划分为两层，即外层目标函数代表未满足零件的最优解，内层目标函数代表颜色更换的最优解，使模型能够完成多目标问题最优解的寻找。

3.3 染色体编码

本文采用坐标编码的方法，编码的X用来表述零件种类，编码的Y则表述颜色的种类，即可做到将83种具体的零件与坐标一一对应。颜色编码、产品编码分别如表1、表2所示。

表1 颜色编码

表2 产品编号

如光耀蓝门槛A则表示为（20,2）。由于X∈[0,30]，Y∈[0,9]，共有31*10=310种坐标组合，但零件个数仅为83种，即有227种坐标组合并不存在对应零件。于是我们设计生存矩阵，将不存在的零件数设为“0”，存在的零件数设为“1”，每生成一个坐标组合，则需通过生存矩阵判断其是否存在。若不存在，则重新生成，直至其判断为是存在的零件种类。有此编码后，问题的约束规则也可以得到解决，即当出现违反问题约束的零件摆放时，重新随机或空一个滑橇来保证满足约束条件。

3.4 种群初始化

进行合适的种群化选择可以避开有效基因的损失，设置合适的遗传算法计算参数将推进算法的进程，参数设置如下。

（1）群体规模N=200。即在内层每次运行过程中，最多保留的种群为200组。

（2）内层迭代次数T1=303。因为一圈传送带中共有303个滑橇，于是每圈的迭代次数设定为303，迭代303次表示单圈完成。

（3）外层迭代次数T2=1000。即在1000个内层迭代出的可行解中，选择最优的作为全局最优解。

（4）变异概率P=0.4。为增加零件多样性，防止陷入局部最优解，设定变异概率为0.4，当产生变异时，颜色变异概率为Pc=0.3，零件种类变异概率为Pz=0.7。

3.5 目标函数

1）内层目标函数

为了降低生产成本，我们需要尽量减少换色次数。函数表达式为：由于支架数量具有上限，即在每圈的喷涂过程中相应的零件数同样具有上限，为在有限的零件数内有效利用支架数，需增加零件的多样性，故更换零件次数需要达到最大值：

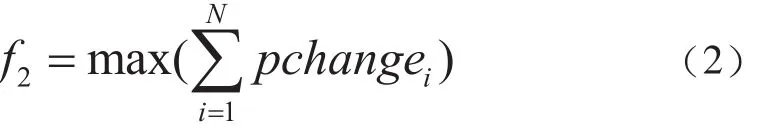
权系数的产生，我们通过层次分析法得到，利用换色次数与零件更换次数两个指标建立判断矩阵进行相对重要度计算。采用求根法来计算特征值的近似值，最终得到权重为W1=W2=0.5。则最终的目标函数为：

2）外层目标函数

由于最终问题的要求是尽量满足生产需求，在内层目标函数选择后的多个可行解中，选择最少的未满足产品零件个数。

3.6 遗传算子的设计

1）非变异交叉操作

由编码规则可知，一个算子由产品种类X和颜色Y组成。假设一个初始选择的算子编码为（n,m），则记这个初始算子为A(n,n)，简记为Anm。在非变异交叉操作中，子代没有发生改变，即复制行为占整个分裂行为的0.6。

如对A74A12进行复制，复制一次得到A74A12A12，复制两次得到A74A12A12A12。

2）变异交叉操作

在遗传算法的计算过程中，变异算子是遗传算法生产新个体的主要操作方式，它能提高遗传算法的全局搜索性，也能从局部得到更优的解。

在复制操作中，我们假设了一个初始算子为Anm，继续沿用在变异操作中。在整个遗传算子的分裂中，变异占据了剩下的0.4，由于一个算子由产品种类X和颜色Y组成，变异时只会在X和Y中选择任意一个。要使得换色次数尽量少并且合理安排产品排序，则Y变化要尽量少。基于问题中隐含的产品种类多样性和产品颜色稳定性的要求，设定算子变异X的概率在变异事件中为0.7，算子变异Y的概率在变异事件中为0.3。

最后，将约束规则进行模型化处理，采用轮盘赌选择方法来达到筛选的目的，通过目标函数值之间的比较，选择函数值最小的组合，作为本圈的初步喷涂计划。由于在换色过程中要求在两个滑橇之间插入一个滑橇的底漆件作为过渡，即意味着换色过程中将会“损失”一个滑橇。

于是我们在确定初步喷涂计划后，减去当圈的换色次数C，即需要删除计划中最后C个滑橇的零件，再一次性插入换色的滑橇之间，形成完整的单圈喷涂计划。

4 结语

根据实例仿真，最终得到平均每圈的换色次数为6.125，未满足生产需求的零件个数为451，说明基于遗传算法的车间调度解决方案能够良好地解决车间生产调度相关问题。