三峡库区马尾松(Pinus massoniana)林林分结构特征对灌木层物种多样性的影响
胡文杰,潘磊*,雷静品,唐万鹏,庞宏东,崔鸿侠,王晓荣
1. 湖北省林业科学研究院,湖北 武汉 430075;2. 中国林业科学研究院林业研究所,北京 100091
林分结构特征和物种多样性是评估森林生态系统功能和林分经营质量的关键指标(Burrascano et al.,2011;方升佐等,2012)。灌木层作为森林生态系统的组成部分,对保持生态系统功能稳定性具有重要作用,其物种多样性在提高林分水源涵养能力、改善土壤养分状况等方面(褚建民等,2007)发挥着不可替代的作用,甚至对乔木层的自然更新也会产生一定的影响(杜忠等,2016)。乔木层林分结构在一定程度上决定了林内个体间的空间生态位(袁士云等,2010),对林内透光条件、土壤基质活性及林内微环境等(燕亚飞等,2014;黎芳等,2016;周晓果等,2017)有明显的影响,进而导致林下植被生长情况发生变化。因此,研究林分结构特征对灌木层物种多样性的影响对实现生态系统健康发展具有重要意义。
林分结构包括空间结构和非空间结构。林下物种多样性影响因素的研究主要集中在海拔、坡度、环境、土壤等(唐志尧等,2004;王顺忠等,2005;王家鸣等,2018),关于林分结构对林下物种多样性的研究相对较少。这些研究对于了解不同地理气候区域的物种多样性状况具有重要作用,但在特定环境条件下难以通过经营调控这些因子达到提高多样性的目的。所以,如何在特定的环境条件和立地条件下通过改善林分结构以提高物种多样性、促进林分健康稳定生长是值得研究的重要课题。
林分结构对林下植被多样性具有明显影响(张建宇等,2017;冯琦雅等,2018)。朱光玉等(2018)对栎类林的研究结果表明,混交度对灌木层物种多样性的影响力最大,但其他林分类型的林分结构对灌木层物种多样性的影响有待进一步开展。马尾松林是三峡库区重要的防护林之一,本研究以该地区马尾松林为研究对象,在全面分析林分结构特征的基础上,通过因子分析、典型相关分析等耦合林分结构综合特征与灌木层物种多样性的关系,以期在经营管理中,为提高库区马尾松林灌木层物种多样性、维持生态系统稳定性提供理论依据。
1 研究区概况
秭归县(110°0′-110°18′E,30°38′-31°11′N)位于湖北省宜昌市,地形整体上西南部高于东北部,属于典型的长江三峡山地地貌。气候条件属于亚热带大陆季风气候,年均温 18 ℃左右,雨量充沛,海拔高度差达1400 m以上,气温随海拔梯度变化明显。本研究中的马尾松林为 1970年代的飞播林,平均海拔1200 m左右,无人为经营,极少受到人为干扰,植被都以自然演替为主,土壤类型为黄壤。乔木树种主要有马尾松、亮叶桦(Betula luminifera)、檫木(Sassafras tzumu)、木姜子(Litsea pungens)、漆(Toxicodendron vernicifluum)等,林分平均胸径15.23 cm,平均树高11.51 m,林分密度950-1600 plant·hm-2。灌木层物种主要有宜昌荚蒾(Viburnum erosum)、高粱泡(Rubus lambertianus)、野蔷薇(Rosa multiflora)等。
2 研究方法
2.1 样地设置与调查
样地设置在秭归县国有林场,在同一坡面以样带形式选取立地条件相对一致的 15块马尾松标准样地,面积20 m×20 m,样地都位于中坡位。对样地内所有胸径≥5 cm的树挂牌,对所有挂牌的树进行每木检尺,测量指标包括胸径(DBH)、树高(H)、枝下高、东南西北方向冠幅等,设置5 m缓冲区,用全站仪定位,获取结构单元中对象木与邻近木的信息。在每个样地的4个顶角及中心处设置5个2 m×2 m的灌木样方,记录样方内属于灌木层的所有物种的名称、盖度、频度等信息。
2.2 林层划分
林层划分采用树冠光竞争高度(CCH)法,该方法考虑了不同高度层树叶在光合作用中贡献差异的生态学现象,根据树高和冠长确定林层的高度。本研究将林分分为上林层、中林层和下林层,计算公式为 CCH=α·CL+UB,其中,CL为冠长,即树高与枝下高的差值,UB为枝下高,α为截止系数。以高度低于下林层最低高度的林木个体数不超过林木个体总数的10%为准,结合本文数据实际情况,截止系数取0.4。具体方法参照郑景明等(2007)和陈科屹等(2017)。
2.3 结构特征参数及多样性指数的计算
本研究选取胸径、树高、枝下高、冠长、冠幅、林层指数、开敞度、竞争指数、空间分布密度指数、角尺度、大小比数、混交度及林分密度等 13个参数反映林分结构综合特征。部分参数计算方法及含义如下:
(1)冠幅(CW)
本研究中的冠幅取东、南、西、北4个方向的平均值(符利勇等,2013),计算公式为:

式中,CW东、CW南、CW西和CW北分别代表东、南、西、北方向冠幅长度。
(2)林层指数(S)
林层指数表达的是林层的垂直结构,其反映了空间结构单元中林层的垂直分布格局及林层多样性(Lv et al.,2012;曹小玉等,2015),计算公式为:

式中,zi表示以对象木 i为空间结构单元中的林层个数;当对象木i与相邻木j属于同一层时,Sij=0;当对象木i与相邻木j不属于同一层时,Sij=1。其值越大代表林层的垂直结构越复杂。
(3)开敞度(K)。
开敞度是用来反映林内的透光条件的指标(汪平等,2013),计算公式为:

式中,Dij为对象木i与相邻木j之间的水平距离,Hij为对应相邻木j的树高。
(4)林木竞争指数(CI)
竞争指数反映了林木个体所承受的来自相邻木的竞争压力大小(李建军等,2010),计算公式为:

式中,CIi为对象木i的竞争指数,di和dj分别为对象木i和相邻木j的胸径,Lij代表对象木i与相邻木j之间的距离,LD代表空间结构单元中4株相邻木与对象木的距离平均值,n为竞争木株树。
(5)水平分布格局
林分水平分布格局选取林木空间分布密度(D)(Hui et al.,2004)和角尺度(W)(惠刚盈等,2004)两个指标,其计算公式分别为:
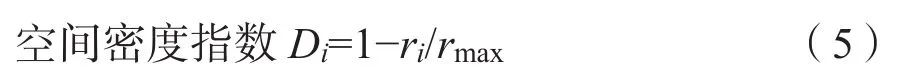
式中,ri为对象木i包含相邻n株树时的最小半径,rmax为林分中两株相邻树木之间的最大距离;
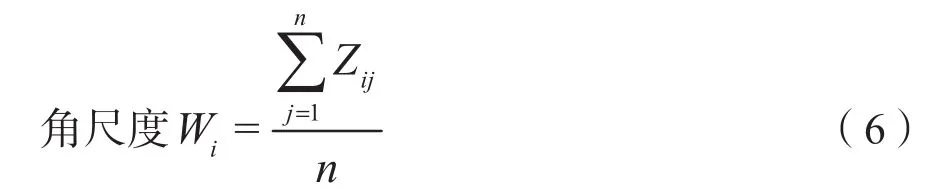
式中,n为相邻木株数,当对象木i与相邻木j的夹角小于标准角时,则Zij=1,否则Zij=0。
(6)大小比数(U)
大小比数反映的是林木大小的分化程度(惠刚盈等,1999),本研究以胸径大小来表征,计算公式为:

式中,n为相邻木株数,当对象木i比相邻木j小时,则Kij=1,否则Kij=0。
(7)混交度(M)
混交度用来反映树种隔离程度的指标(唐万鹏等,2015),其值越大表明树种混交程度越高。计算公式为:

式中,n为相邻木株数,若对象木i与相邻木j的树种不同,则mij=1,否则mij=0。
(8)灌木层多样性指标
在耦合林分结构与物种多样性的关系时,应综合选取与多样性相关的各种指标体系(张建宇等,2017),本研究选取Margalef丰富度指数(R′)(袁士云等,2010)、丰富度(Richness)、Shannon-Wiener指数(H′)、Pielou均匀度指数(J)和Simpson多样性指数(S′)(Hu et al.,2016)等5个指标反映灌木层多样性情况。计算公式如下:
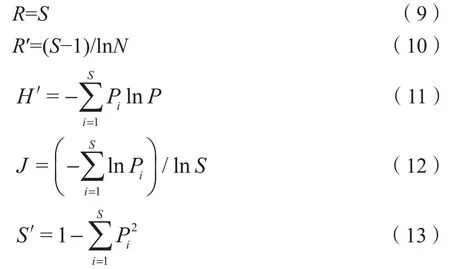
式中,S为物种数,N为所有物种的个体总数,Pi为物种i的重要值。
不同林层林分结构特征见表1。
2.4 因子分析及典型相关分析
在因子分析中,采用 KMO(Kaiser MeyerOlkin)量度对主成分分析的结果进行检验,一般认为KMO值要大于0.5,如果小于0.5则需要剔除异常变量或引入与异常变量有关联的其它变量(高慧璇,1997)。主成分分析结果中,特征值接近0的主成分具有多重共线性,此时可将特征值接近0的主成分中权重较大的变量剔除,再用剩余变量重新进行主成分分析,直到KMO值满足一般条件(袁志发等,2002)。
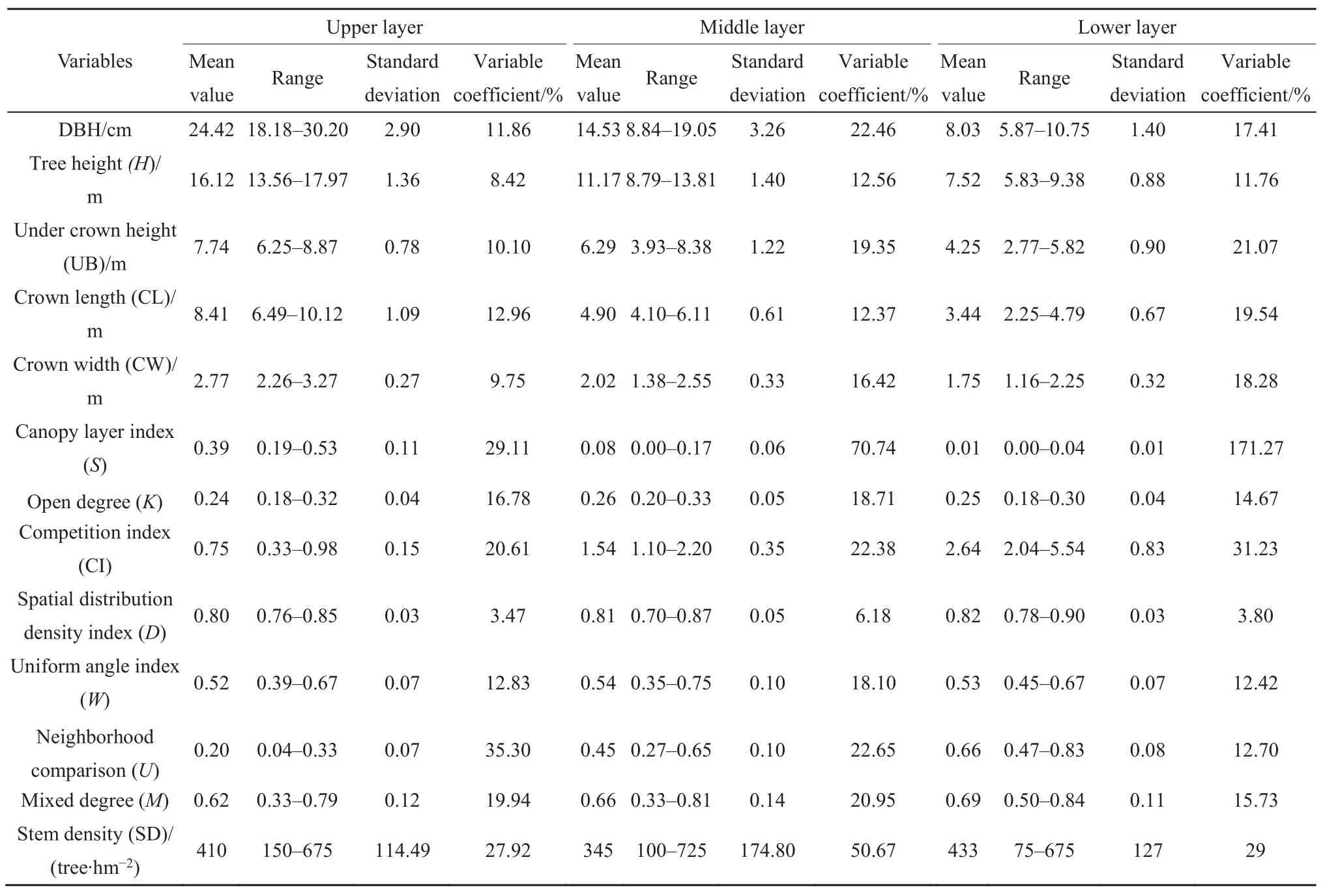
表1 不同林层林分结构特征统计Table 1 Statistical of forest structure characteristics for different layers
典型相关分析可用来判断两组变量之间的相关性,即使变量组 ui=ai1x1+ai2x2+ai3x3和 vi=bi1y1+bi2y2在线性组合ui和vi的方差为1的约束条件下,让其相关系数达到最大(朱光玉等,2018)。本研究通过因子分析构建反映林分结构特征和灌木层多样性的因子,提取具有最大相关性的线性组合并得到典型相关系数。
Pearson简单相关分析、主成分分析和典型相关分析在SPSS 22.0中完成。
3 结果与分析
3.1 灌木层群落特征
灌木层Shannon-Wiener指数、Margalef指数、Pielou指数、Simpson指数和丰富度的平均值分别为 2.04、1.67、0.83、5.93和 12.07。共有 44个物种,其中,耐阴物种、阳性物种和中性物种的个数分别为6个、13个和25个。在耐阴物种中的乔木种有1个,为檫木,在阳性物种中的乔木种有化香树(Platycarya strobilacea)、亮叶桦和山樱花(Cerasus serrulata),在中性物种中的乔木种有梾木(Swida macrophylla)、茅栗(Castanea seguinii)、木姜子、漆、青麸杨(Rhus potaninii)和香椿(Toona sinensis)。各样地灌木层物种重要值排名前三的物种主要有木姜子、高粱泡(Rubus lambertianus)、宜昌荚蒾(Viburnum erosum)、桦叶荚蒾(Viburnum betulifolium)、麻核栒子(Cotoneaster foveolatus)、檫木、亮叶桦、漆、湖北算盘子(Glochidion wilsonii)、蜡莲绣球(Hydrangea strigosa)和中国旌节花(Stachyurus chinensis)等。
3.2 林分结构与多样性指数相关性分析
Pearson相关性检验结果表明(表2),林分总体结构特征各参数与多样性指数均无显著相关性(P>0.05)。在中林层和下林层,Simpson指数分别与树高和胸径呈显著正相关(P<0.05),Pielou指数则在下林层中与林木竞争指数负相关(P<0.05),与林分密度正相关(P<0.01),而其他多样性指数与结构特征则无显著性关系。但在上林层,各多样性指数均与林分结构表现出显著或极显著关系,Shannon-Wiener指数随着上林层树高及枝下高的增大而增大(P<0.01),Pielou指数和Simpson指数与上林层胸径、树高、枝下高、冠长呈显著或极显著正相关;上林层的垂直结构越复杂,对应的Pielou指数越高;林木混交度越大,对应的Simpson指数越小;林木大小分化程度越高,混交程度越低,Margalef指数与丰富度越大,Margalef指数与枝下高表现出显著正相关,丰富度R与其的相关性则未通过显著性检验。综上,上林层是影响灌木层多样性的关键层次,因此,在后续分析中都以上林层的结构特征参数为基础进行统计分析。
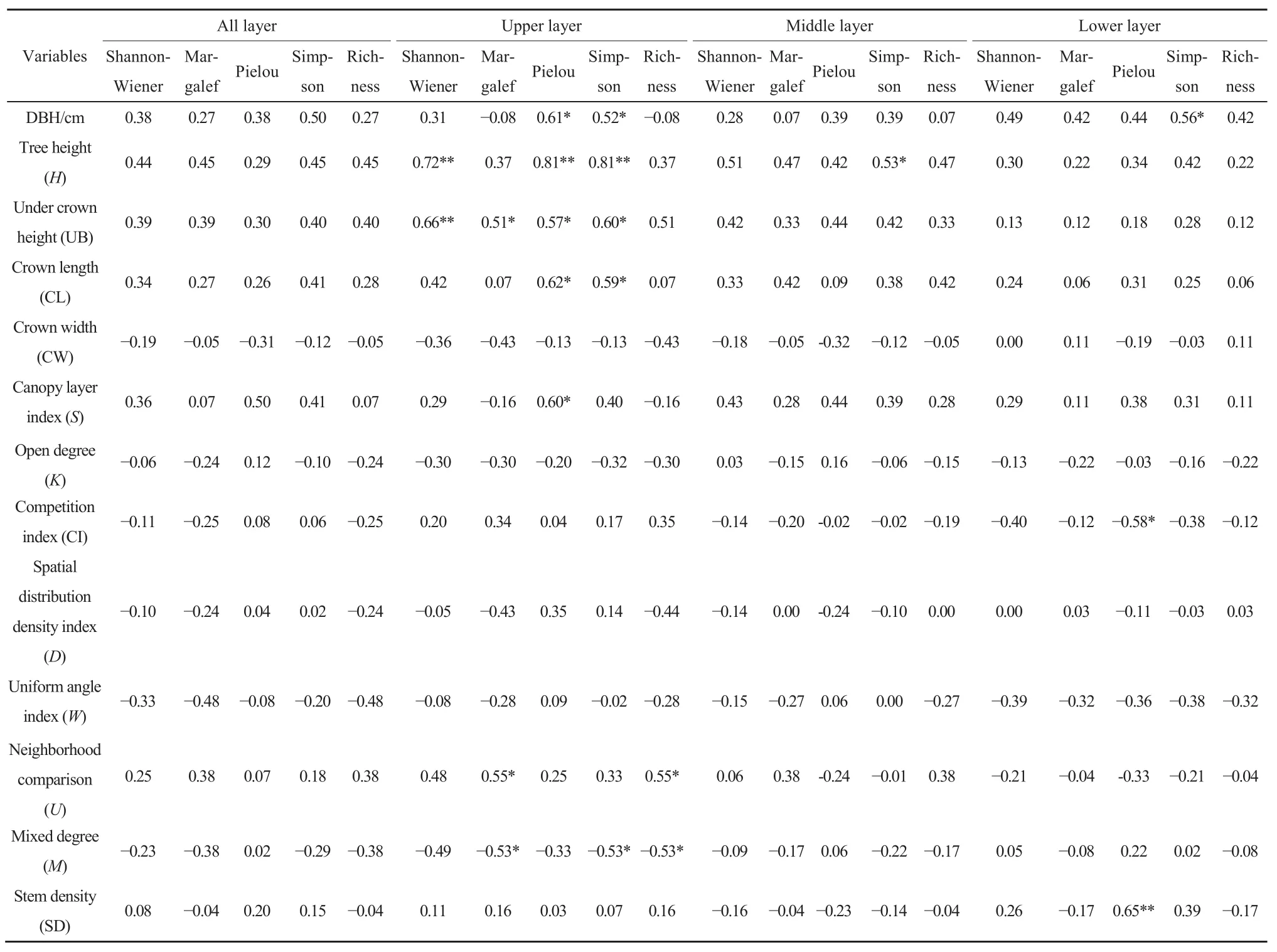
表2 林分结构特征与多样性指数相关分析Table 2 Correlation analysis between forest structure characteristics and diversity index
3.3 多元逐步回归结果
在相关分析的基础上,以上林层结构特征参数为自变量,以多样性指数为因变量进行多元逐步回归,从而保留影响灌木层物种多样性的主要解释变量,由于Margalef丰富度指数和丰富度代表的意义较为接近,故多元逐步回归中仅以Margalef代表。从表3可以看出,Shannon-Wiener指数、Pielou指数及Simpson指数的回归方程中,都剔除了树高而保留了其它所有变量,Margalef指数回归方程则仅剔除了大小比数。这说明灌木层物种多样性受到了多种林分结构特征的综合影响。
3.4 因子分析
对林分结构变量和多样性指数分别做主成分分析。采用KMO量度筛选变量,剔除具有多重共线性的变量,以达到多指标降维的目的。对 13个林分结构变量做因子分析,其KMO=0.282,此时删除特征值为0.000的成分中权重最大的树高变量,再以相同方式对剩下的 12个变量做因子分析,此时删除特征值=0.010(接近于 0)的成分中权重最大的枝下高变量,再做因子分析,此时KMO=0.505,大于一般基本要求的 0.5,且最小的主成分特征值为0.19,不可视为接近于0。因此,采用保留的11个变量进行主成分分析,选取特征值大于1的主成分,最终保留3个主成分,其旋转后因子载荷表见表 4。对反映多样性的 5个指数做因子分析,KMO=0.721,符合基本要求,保留了2个主成分,其旋转后因子载荷表见表5。
从表4可以看出,上林层林分结构特征变量可分为3类因子,在第1类因子中,开敞度、林木竞争指数、大小比数、混交度及林分密度的载荷绝对值较大,这些变量分别反映了林木的透光条件、林木承受的竞争压力、林木大小分化程度、树种隔离程度和林分的稀疏状况,这些变量基本都是林木通过自然竞争后的结果,反映了林分中林木的竞争状态,因此,可将第1个类因子定义为林分竞争状况因子。第2个主成分中则是林木空间密度、角尺度以及冠幅的载荷值较大,由于前两个变量反映了林分水平空间分布格局,因此可将其定义为水平结构及冠幅因子。第3个主成分中,胸径、冠长及反映林层垂直结构的林层指数载荷值较大,因此,将该主成分定义为垂直结构及生长因子。从表5可以看出,多样性变量指标可分为2类因子,即丰富度因子和多样性因子。

表3 多样性指数与上林层结构特征的多元逐步回归Table 3 The multiple stepwise regression model with diversity index and the structural characteristics of the upper layer
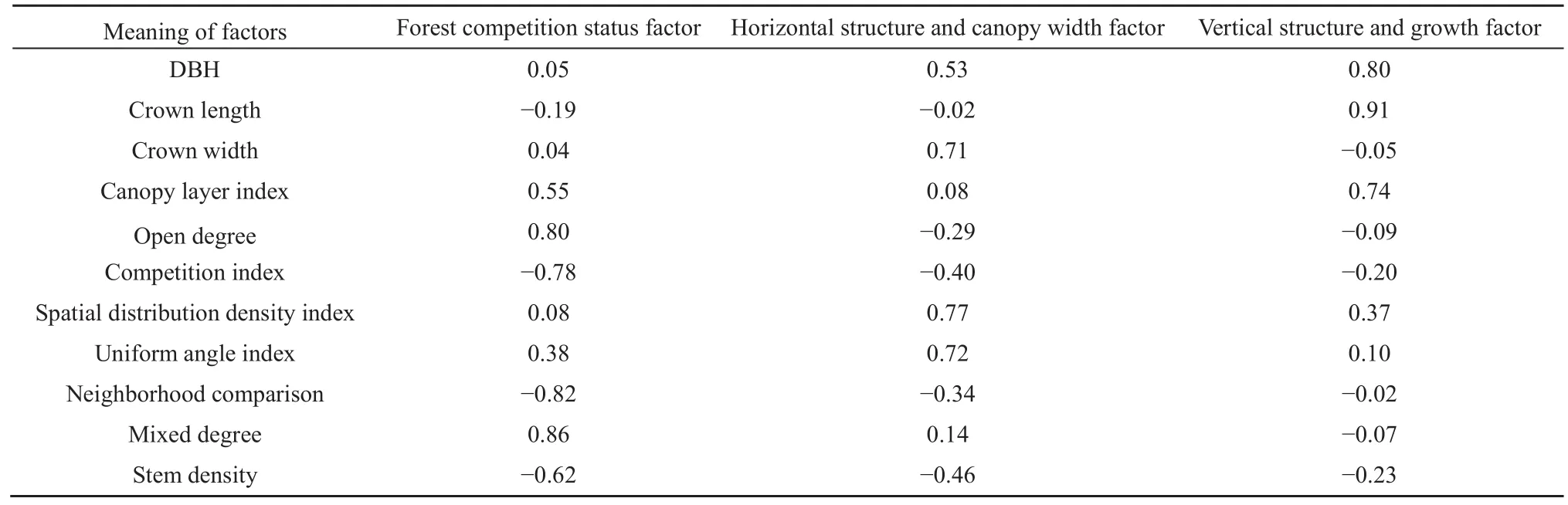
表4 旋转后林分结构因子载荷Table 4 The loading values of forest structure factors after rotation
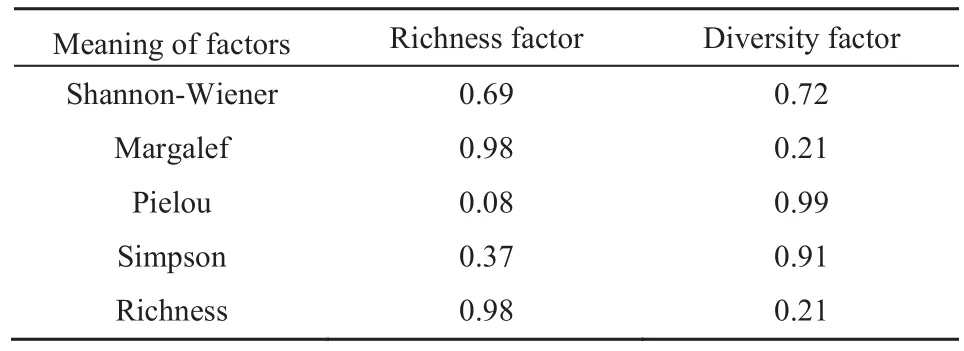
表5 旋转后多样性指数因子载荷Table 5 The loading values of diversity index factors after rotation
3.5 典型相关分析
根据以上因子分析可得到每个样地的3个林分结构因子和2个灌木层多样性因子的标准化因子得分,并以此为基础进行典型相关分析,结果共得到2组典型相关结构(表6),其中,第1典型相关结构通过显著性检验(P=0.014),典型相关系数为0.822,这表明上林层林分结构特征与灌木层多样性总体上有较强的相关性。从表6可以看出,反映林分结构特征的3个因子中,垂直结构及生长因子的载荷最大,为 0.962,表明该因子是影响灌木层多样性的主要因子,且灌木层多样性随着该因子的增大而变丰富。其次是林分竞争因子,其载荷为-0.265,说明灌木层多样性随着该因子的增大而变小。而灌木层多样性对水平结构及冠幅因子的敏感性则较小。
4 讨论
林下植被生长情况是多种因素共同作用的结果,其多样性很大程度上受到了林分演替阶段、过程及空间异质性等对生境改造的影响(鱼腾飞等,2011)。乔木层作为森林生态系统的重要组成部分,其生长状况可对林分空间异质性(黎芳等,2016)、土壤条件及微气候(Uliassi et al.,2002;Rodríguezcalcerrada et al.,2008)等产生影响,从而导致林下物种多样性发生变化(Lhotka et al.,2008;Parker et al.,2008)。Pearson相关分析表明,林分总体结构特征各变量均与灌木层多样性无显著性关系,分林层后发现中林层和下林层的结构特征与灌木层多样性有较微弱的关系,而上林层中的结构变量则与灌木层多样性有较丰富的显著相关性,这在一定程度上表明了林下植被物种多样性影响因素的复杂性(刘冠成等,2018)。上林层对整个林分的树种组成有关键作用(玉宝等,2015),在本研究中,上林层的蓄积量占整个林分蓄积的74.73%,该层次多由林分中径级较大的林木组成,在自然状态下,大径级林木(喻理飞等,2002)的生物量与凋落物量相对较多(王莉莉等,2014),对土壤及整个生态系统的养分循环有重要影响,而土壤条件又与物种多样性有密切关系(王顺忠等,2005),且上层林木对林内光照分布及物种生态位有明显影响(欧芷阳等,2017),这在一定程度上解释了灌木层物种多样性与上林层的结构特征的关系更为紧密的原因。
采用多元逐步回归的主要目的是为了排除干扰变量而保留解释变量(Hu et al.,2018),本研究中,保留的 12个结构特征变量分别解释了 Pielou指数、Simpson指数和 Shannon-Wiener指数的62.3%、63.0%和47.4%,而仅解释了Margalef指数的24.6%。朱光玉等(2018)采用混交度、聚集指数和开敞度等3个林分结构特征变量与多样性指数作多元逐步回归的结果显示,这3个变量仅解释了Auclair&Goff多样性指数的23.3%和Pielou指数的16.3%,Margalef则未能通过回归方程的显著性检验。该结果与本研究结果对比表明,灌木层物种多样性是林分结构多种特征共同作用的结果。
为探索林分结构的变量组合与灌木层多样性之间的关系,本文采用了典型相关分析。结果表明上林层林分结构特征和灌木层多样性之间存在显著的相关关系,其中垂直结构及生长因子的影响最大,即胸径越大、冠长越长,林层的垂直结构越丰富,灌木层多样性就越高。这主要是因为处于上林层的大树能够获得更好的光照条件,并且能够产生更多的凋落物,与土壤间的养分流动更多,从而提高了土壤有机质含量,而土壤孔隙度、蓄水量及养分等会随着土壤有机质的提高而增大(王莉莉等,2014),这些都是影响灌木层植被生长的潜在因素。垂直结构越复杂,林下的光照可能会更强(Pelt et al.,2000),从而提高了物种多样性(蒋政等,2015)。林分竞争因子整体与灌木层多样性呈负相关,这可能是由于林分竞争越激烈,对于有限资源的利用就越充分,灌木的生长由此受到影响。有研究认为,林分混交度越大,其对应的灌木层多样性越高(朱光玉等,2018),然而在本研究中,多元回归方程和典型相关分析结果都显示灌木层多样性随混交度的增大而减小,这与林分类型有较大的关系,马尾松林混交度越低,其透光性越好,越利于林下层植被的生长(刘延滨等,2012),这与张建宇等(2017)对落叶松林的研究结果类似。此外,还与灌木层树种特性有关(何友均等,2013)。

表6 典型相关分析结果及各因子的典型载荷Table 6 The results of canonical correlation analysis and typical loads of each factor
曹梦等(2018)在研究马尾松飞播林林下物种多样性与环境因子关系时,选取了包括海拔、株数密度、石砾含量、平均胸径等 20个生物因子和非生物因子,以前向选择和蒙特卡洛检验法进行关系耦合,最后得到了9个影响因子,解释了物种多样性变异的70.9%,并得出生物因子是影响多样性的主要因子的结论,这与本研究的结果具有一定的相似性。典型相关分析对样本数量和变量个数有一定的要求,如果变量过多而样本数量不足时,其分析效果会受到较大的影响。因此本研究通过因子分析将变量进行了降维分类,取得了较好的效果。
5 结论
在马尾松林中,上林层是影响灌木层物种多样性的主要层次,灌木层物种多样性受到该层次多种林分结构特征的共同影响。上林层林分结构可分为3类,其中,垂直结构及生长因子对灌木层物种多样性的影响最大,表现为正相关关系。在经营管理中,可通过调控上林层的胸径、冠长及冠层垂直结构以达到提高林分灌木层物种多样性的目的。

