中学三角函数在解题中的应用研究

◆荀光玲

(烟台高级师范学校)

对于中学学生而言掌握三角函数知识点，并熟练运用三角函数进行解题具有重要的意义。学习三角函数可以提高抽象思维能力。三角函数可以将图形的边长关系、角度关系通过公式表达并建立关系，有助于学生在数形之间变换。三角函数将抽象的图形转化为公式、代数的形式进行表达。通过数学表达之间的变换、整理、计算，无形中增加学生的计算渠道，培养了计算能力。

一、三角函数解题的基本应用

1.代数解题中的应用

三角函数在解题中的应用是指将代数问题通过三角函数转换，将原问题转化为三角函数问题，利用三角函数的定义、性质和相关定理进行解决问题。对于部分复杂的代数问题进行三角函数转化后，可以达到化难为易、化繁为简的效果，为解决代数问题提供捷径。

选择合适的三角函数进行代换是三角函数解决代数问题的关键。进行三角函数转换时，首先应从题中变数的允许值去考虑；再从解题的需要通过分析，选择合适的三角函数进行代换。在进行三角代换后，再根据所求问题，采取对应的三角函数的性质进行求解。

2.几何解题中的应用

三角函数在几何解题中的应用，就是讲几何问题转化为三角函数问题，运用三角函数的性质、定理完成几何命题的证明或求解。对于某些几何问题在证明或者求解时往往比较复杂，无法应用几何定理直接解决。然而，将上述问题三角化后，理论三角函数的性质进行解题，不仅证明过程简捷，而且证明思路也比较自然，易于证题。

3.最值解题中的应用

三角函数在最值解题中的应用是指将原函数中的自变量进行适当的三角函数化后，利用三角函数周期性、最值性等性质，求解原函数的最值问题。因为目标函数为有界函数，因此可以进行适当的变换，将解析几何最值问题转化为三角函数的最值问题。本题型的解题关键为将原来目标函数进行三角化后，并灵活地选择变量，运用三角函数解析后，建立原目标函数的三角函数表达式。

二、三角函数解题常见问题

1.基础理论知识掌握不扎实

对基础知识的扎实掌握是解题的基础和关键。主要体现在以下几个方面：首先，对三角函数基本含义的掌握不理解，或者对有些问题模棱两可。其次，缺乏主动性导致知其然，但不知其所以然。这势必导致学生在解题中，对于未遇到的过的题缺乏应对能力。

2.三角函数问题分析能力不足

分析能力是解决三角函数问题必须培养的一种能力，然而现实中学生在解题和教师在授课中往往忽视了这一点。对于很对学生和老师，当遇到问题时常常不去思考，而是机械性、惯性的去解题。这往往导致问题解决到一半才发现无法再进行下去。这种学习和教学方式虽然增加了做题的工作量，但实际并未提高、培养学生的分析问题的能力。在遇到其它问题时往往不知如何分析或寻找突破口。

三、中学三角函数在解题方法总结

1.定义法

定义法解题是指通过三角函数的基本定义，对问题进行整理、分析，进而得到解决问题途径的一类方法。

例题1：在△ABC中，已知△中三边的长度分别为a、b、c，∠C=90°，求a3cosA+b3cosB？(可以用a、b、c进行表达)。

解题思路：分析可以看出，被处理的式子无法直接进行计算。因为a、b分别代表了数值，cosA、cosB分别表示了两角的函数。可以将上述两种类型的代数，转换为同一种类型的在进行计算。

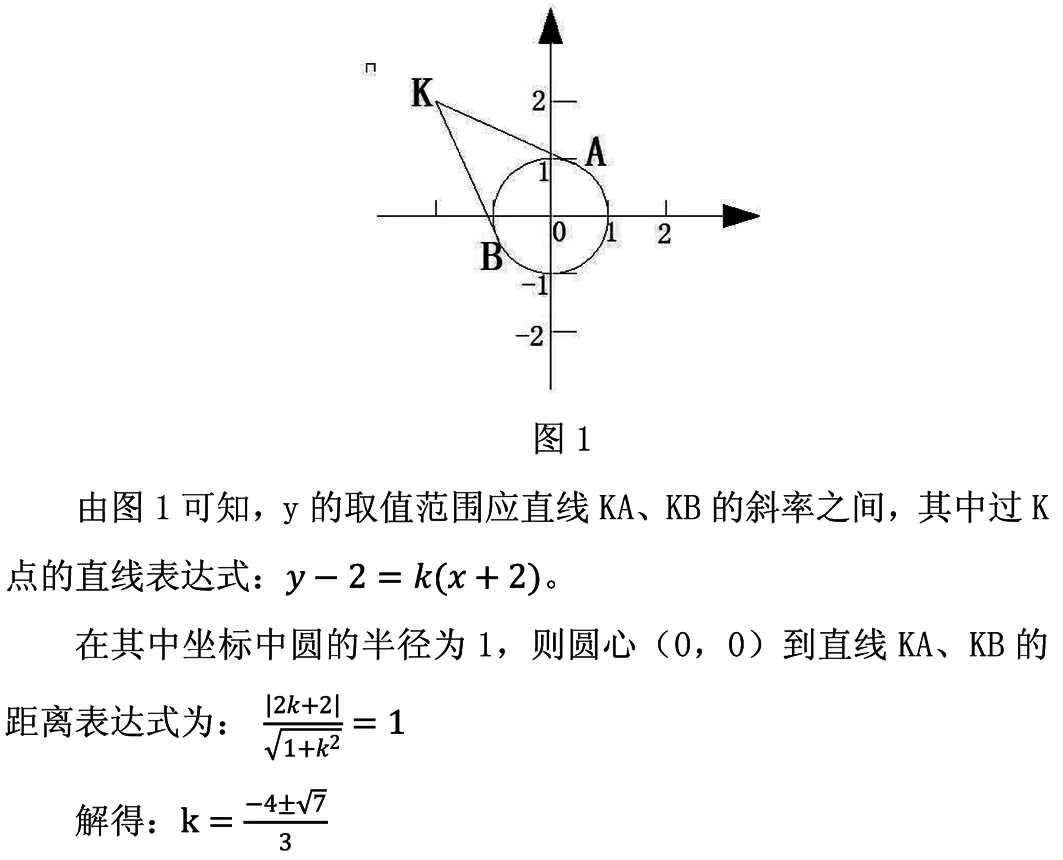
四、结语

运用三角函数解决解题，对于锻炼学生计算能力、思维能力、分析能力等均有较大帮助。引导学生选择正确的方法进行解题，在三角函数解题中十分关键。因此，在日常教学中应常与学生进行沟通，要引导学生面对问题时勤于梳理，对于方法要善于总结，进而提高学生运用三角函数进行解题的能力。