点火增长反应速率方程在LS-DYNA软件中嵌入及应用

苗飞超，周霖，张向荣，曹同堂

(1.北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081; 2.安徽东风机电科技股份有限公司, 安徽 合肥 230000)

0 引言

冲击起爆特性是炸药的重要性能之一，是作用可靠性和使用安全性评价的重要依据。Lee & Tarver点火增长反应速率方程[1-2]已广泛用于冲击起爆的数值模拟,并成功重现了圆筒实验[3]、拉氏分析实验[4-6]、飞片冲击实验[7]、微通道装药爆轰实验[8]的实验结果。但点火增长反应速率方程的参数较多(三项式的参数多达15个)且参数间存在关联[9]，这导致点火增长反应速率方程的标定存在较大的困难。为此，Murphy[9]对反应速率方程的形式进行了修改，得到了参数更少，参数间无关联的反应速率方程。由于改进的反应速率方程保留了Lee & Tarver模型中点火增长的概念，因此两者在模拟冲击起爆方面具有相同的功能。尽管改进的反应速率方程具有以上优点，但目前为止，大型商业软件，包括LS-DYNA、AUTODYN和Abaqus等中并未包含该反应速率方程。

因此，本文将改进的点火增长模型以自定义状态方程的形式嵌入LS-DYNA软件中，并采用此模型对DNAN基熔注炸药的冲击起爆过程进行了数值模拟，通过对比计算压力曲线和实验压力曲线标定了改进的模型参数。

1 改进的点火增长反应速率方程

1.1 模型简介

三项式的Lee & Tarver反应速率方程[2]的表达式为

(1)

式中：F为反应分数；p为压力；ρ和ρ0分别是当前时刻和初始时刻的密度；I、b、a、x、G1、c、d、y、G2、e、g、z、Figmax、FG1max和FG2min为15个可调参数；等号右侧3项分别为点火项、慢速增长项和快速完成项。Murphy[9]保留Lee & Tarver反应速率方程中点火增长的概念，对上述反应速率方程进行了改进。改进的反应速率方程表达式为

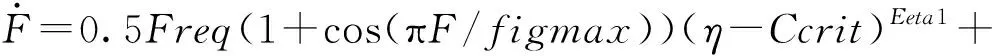
(2)

式中：η=ρ/ρ0-1；Freq、figmax、Ccrit、Eeta1、Grow1、Es1、em、Grow2、Es2、en为10个可调参数。与Lee & Tarver反应速率方程相比，改进的点火- 增长反应速率方程具有以下优点：

1)慢速增长项和快速完成项的系数相关性弱。改进的点火增长反应速率方程用sin(πFEs)代替了Lee & Tarver反应速率方程慢速增长项和快速完成项的(1-F)mFn(m为c或e，n为d或g)。显然，Es只影响sin(πFEs)曲线的形状，峰值大小始终为1.0，而m和n的大小同时影响(1-F)mFn曲线的峰值和形状。换言之，调整曲线的形状时，Lee & Tarver模型需要同时改变2个参数(m和n)，而改进的模型只改变1个参数(Es)，简化了参数的标定过程。

2) 反应速率方程的参数较少。改进的反应速率方程的参数有10个，比Lee & Tarver反应速率方程少5个，进一步降低了参数标定的难度。

1.2 模型嵌入LS-DYNA软件

鉴于改进的点火- 增长反应速率方程具有上述优点，本文将改进的点火- 增长反应速率方程以自定义状态方程的形式嵌入LS-DYNA软件中。下面对自定义状态方程计算中，未反应炸药和爆轰产物的混合法则、状态方程形式和各物理量的求解过程进行介绍。其中状态方程混合采用Cochran等[10]的算法。

部分反应炸药是未反应炸药和爆轰气体产物的混合物，假设两种组分处于压力p和温度T平衡状态，即

(3)

式中：下标m代表部分反应炸药；下标s代表未反应炸药；下标g代表爆轰气体产物。部分反应炸药的相对体积Vm和内能Em，满足加和特性，

(4)

式中：相对体积V=v/v0，v和v0分别是当前时刻和初始时刻的比容；内能E=e/e0，e和e0分别是当前时刻和初始时刻的比内能。

未反应炸药和爆轰产物均采用含温度的JWL状态方程[2]，其形式为

(5)

式中：*为s或g，分别代表未反应炸药和爆轰产物；A、B、R1、R2、ω、CV均为可调参数。

温度、压力和反应分数等物理量的求解过程如下：

1)温度的计算。

为简化计算，将能量方程转化为温度方程。温度方程的表达式为

(6)

式中：Sij为偏应力张量；εij为应变张量；q为人工黏性项；CVm、J以及H分别为

(7)

采用预测- 校正格式对(6)式进行显示差分计算，可得到ΔTm.

2)真实体积分数和压力的计算。

定义β=(1-F)Vs/Vm为未反应炸药的真实体积分数[10]，则Vs和Vg可表示为

Vs=βVm/(1-F)，

(8)

Vg=(1-β)Vm/F.

(9)

由于未反应炸药和爆轰气体产物处于压力平衡，因此

pg-ps=δ(Tm,Vm,F,β)=0.

(10)

在给定Tm、Vm、F的条件下，采用牛顿迭代法对(10)式进行迭代求解，迭代变量为β. 在迭代过程中，通过(8)式和(9)式计算Vs和Vg，并将Vs和Vg代入单组分状态方程中计算ps和pg.β通过迭代收敛时，得到pm=0.5(ps+pg)。

3)反应分数F的计算。

反应速率方程可表示为

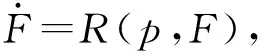
(11)

式中：R为任意函数。本文采用Cochran等[10]的差分格式计算该方程，该格式兼具显示格式和隐式格式的优点，其形式为

(12)

式中：上标n代表第n个时间步；Δt为时间步长；

(13)

(13)式中λ的取值方法可保证反应速率方程的差分求解过程是完全稳定的。各物理量在一个时间步长内的迭代求解过程如图1所示。

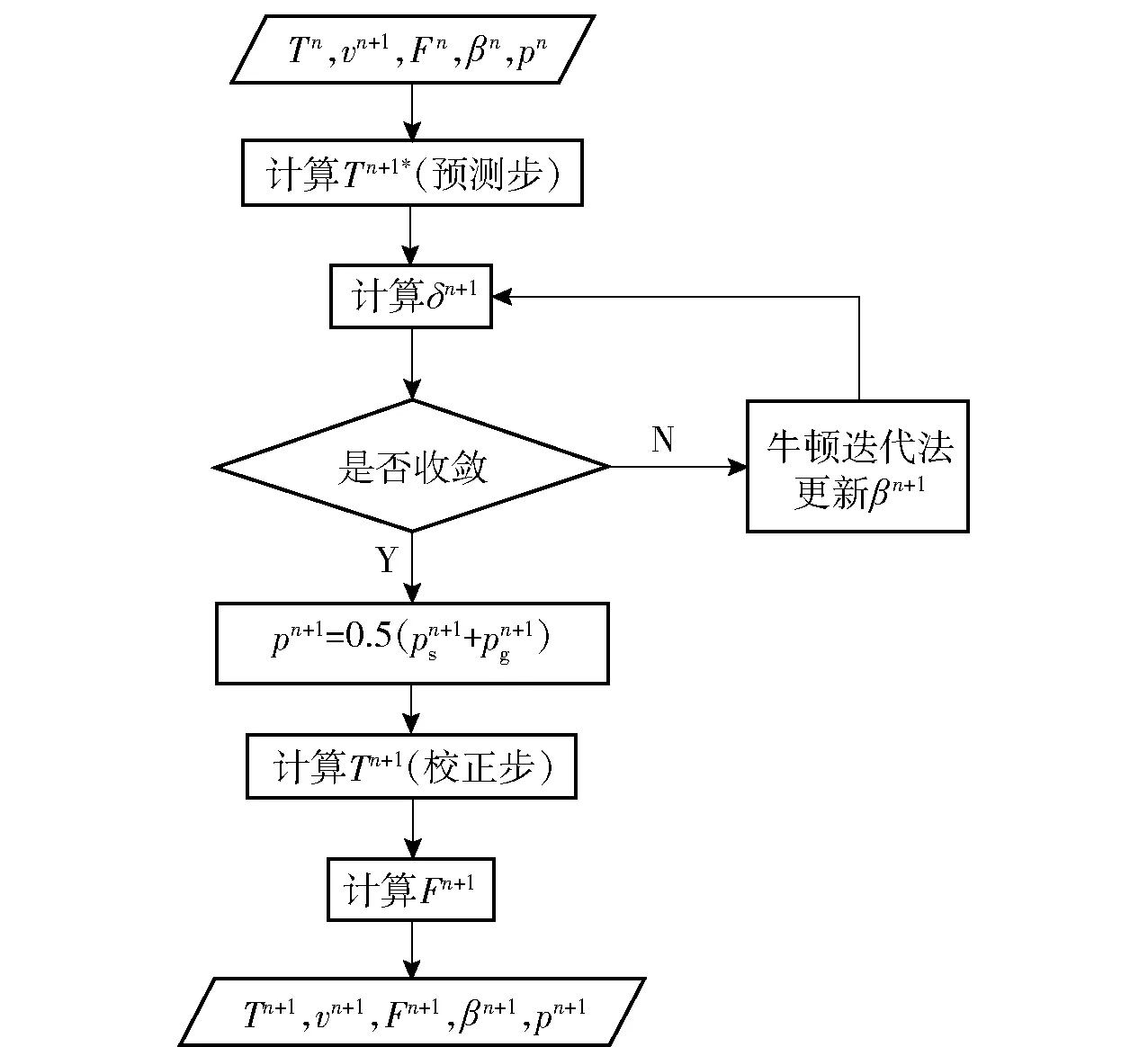
图1 各物理量迭代求解流程图Fig.1 Flow chart of iteration for updating the variables

2 冲击起爆数值模拟

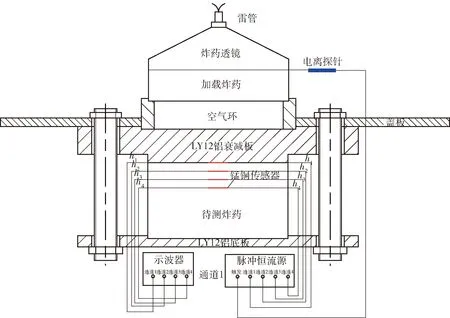
图2 一维拉格朗日分析测试系统示意图[5]Fig.2 Schematic diagram of one-dimensional Lagrange analysis and measurement system[5]

Cao等[11]采用如图2所示的一维拉格朗日分析测试系统，测量了DNAN基熔注炸药(DNAN 29.5%/RDX 40%/Al 30%/N-甲基-4-硝基苯胺(MNA)0.5%)冲击起爆过程中的压力曲线。测试时，由透镜产生的平面波经空气隙和铝板衰减后入射到炸药中。待测炸药由3个厚度3 mm药片和1个厚度20 mm的药片组成，药片直径均为50 mm. 4个锰铜传感器分别安装在距离铝衰减板0 mm(h1)、3 mm(h2)、6 mm(h3)和9 mm(h4)位置处。最终实验得到图2中4个传感器记录的压力曲线。本文以该压力曲线为基础，标定改进的点火增长模型参数。通过对比计算压力曲线和实验压力曲线，验证改进的点火增长模型能否正确模拟DNAN基熔注炸药的冲击起爆过程。

2.1 几何模型

为节省计算内存和计算时间，只建立了待测炸药的几何模型，并将实验测得的图2中衰减板与炸药界面处(即图2中h1)的压力变化历史作为炸药的压力边界条件。图3中4个观测点位置对应图2中4个锰铜传感器位置，即h1(0 mm)、h2(3 mm)、h3(6 mm)和h4(9 mm)，以便将计算值与实验值对比。

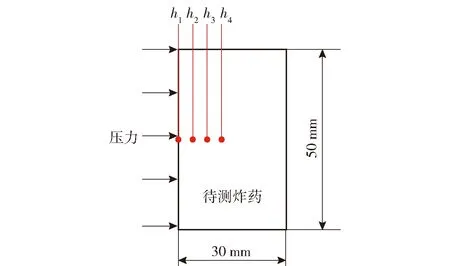
图3 数值模拟几何模型Fig.3 Geometric model of numerical simulations

2.2 材料参数

未反应炸药和爆轰产物状态方程参数来自文献[11]。但文献[11]中未反应炸药采用的是Gruneisen状态方程。考虑到本文采用的是JWL状态方程，因此需要将Gruneisen状态方程拟合为JWL状态方程。本文采用遗传算法对其进行拟合，具体拟合方法见文献[12]。拟合结果如图4所示，拟合参数如表1所示。

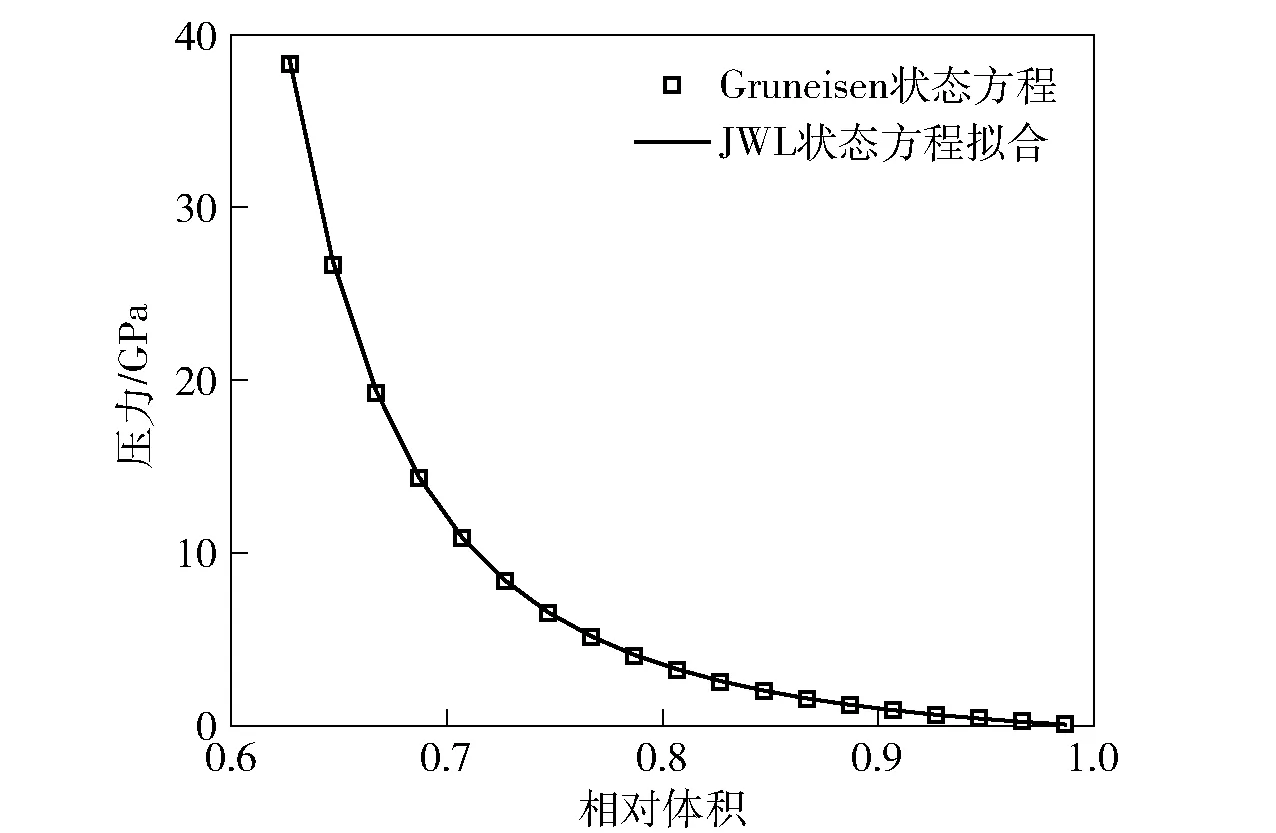
图4 JWL状态方程参数拟合Fig.4 Fitting result of JWL equation of state

反应速率方程参数通过试错法优化得到。通过不断调整反应速率方程参数，减小计算值相对实验值的偏差。最终，优化得到的反应速率方程参数如表2所示。

2.3 计算结果与分析

采用表1和表2中的参数对图3的模型计算，得到的计算值和实验值如图5所示。从图5中可以看出，冲击波到达时间和压力驼峰对应时间重合度较高，计算值与实验值吻合较好。但是，h3和h4处计算的压力峰值与实验值相差较大。这可能是封装传感器的聚四氟乙烯与炸药的阻抗不匹配导致的。因此，在对计算结果进行评价时，应该更多的关注冲击波到达时间、压力变化趋势和驼峰出现位置与实验值是否吻合。从图5来看，改进的点火增长模型能够较好地描述炸药的冲击起爆过程。

表1 JWL状态方程参数

注：DCJ为爆速，pCJ为爆压，E0为内能。

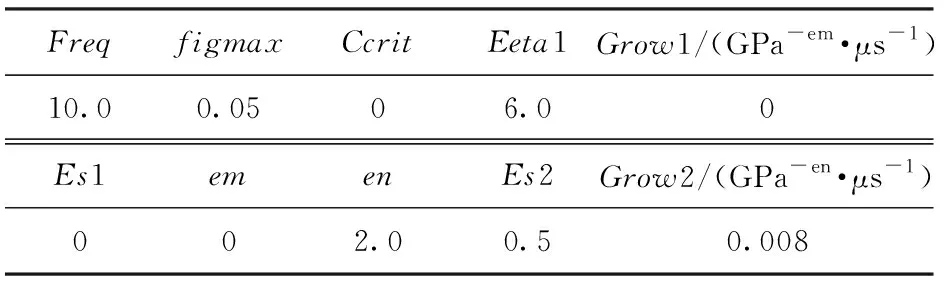
表2 改进的点火增长反应速率方程参数

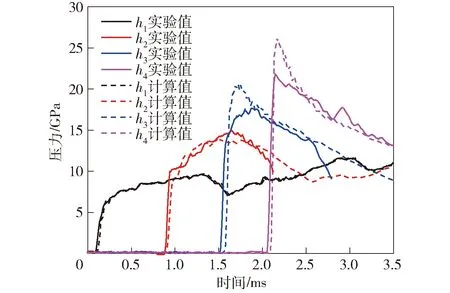
图5 4个观测点处的压力时程曲线实验值与计算值对比Fig.5 Comparison of experimental and simulated values of pressures at four fixed points

相对于软件自带模型，自定义模型可以输出更多的计算信息，有助于判断模型嵌入LS-DYNA软件时采用的压力更新算法是否可行。压力更新算法中迭代变量的选择尤为重要。本文2.2节中，采用牛顿法对(10)式进行迭代求解时取β为迭代变量，并没有取Vs或Vg作为迭代变量，具体原因结合本次数值模拟计算结果分析如下。

图6为本文数值模拟计算得到的4个观测点处未反应炸药相对体积的变化曲线。图6中h2位置处，初始时刻Vs为1，到计算结束时约为33，变化范围较大。因此，如果以Vs作为迭代变量，则迭代次数较多，计算效率低。此外，在传感器有效记录时间内，如果入射到炸药中的冲击波持续时间较短，则稀疏波的作用时间会比较长，Vs可能达到103量级。此时，在对Vs进行迭代时，容易出现不收敛情况，并且由于计算机存在舍入误差，在计算时甚至会出现0/0型的错误。

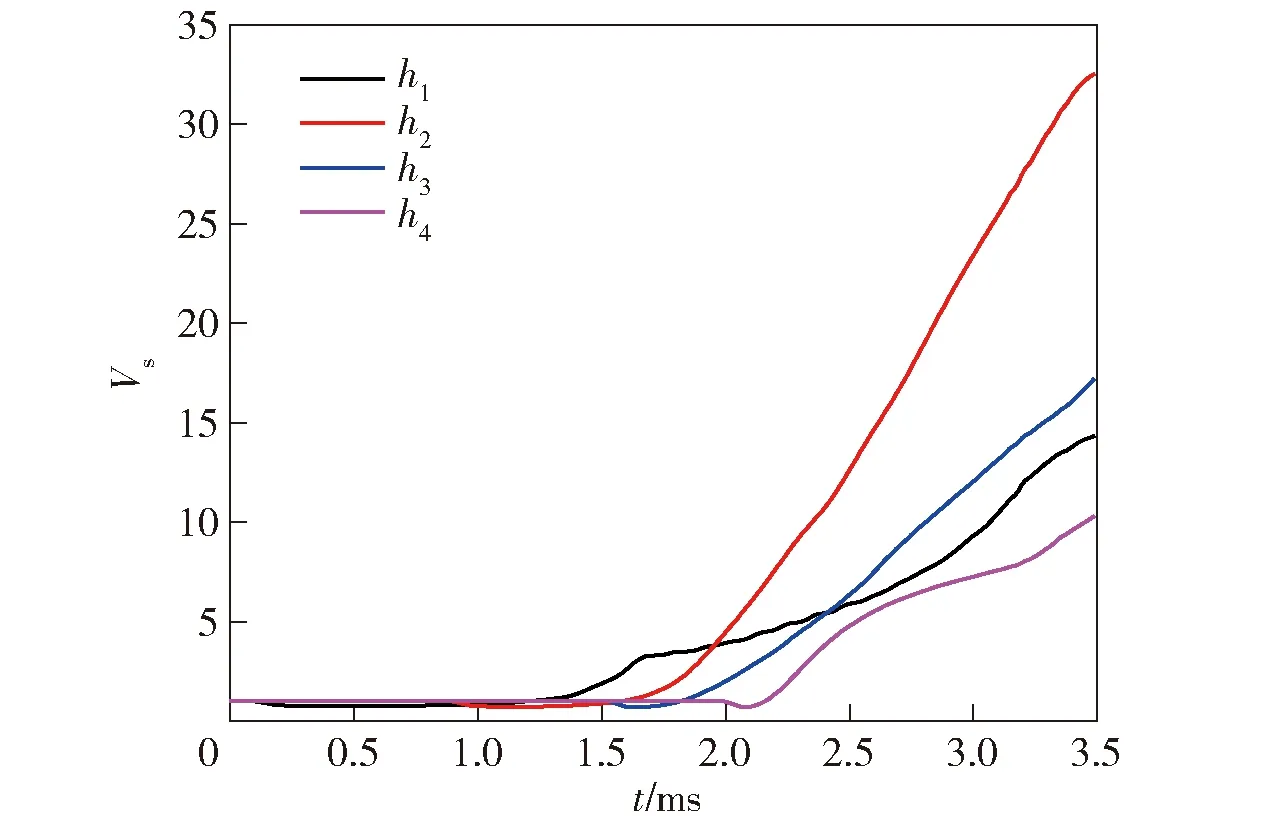
图6 4个观测点处未反应炸药相对体积Fig.6 Relative volumes of unreacted explosives at four fixed points

图7为本文数值模拟计算得到的4个观测点处爆轰产物相对体积的变化曲线。由图7可知，Vg的变化范围较小，将其作为迭代变量似乎可行。但是，在波阵面处，Vg的变化极为剧烈，类似于跳跃间断点。因此，若将Vg作为迭代变量，在波阵面处进行迭代时很难收敛。

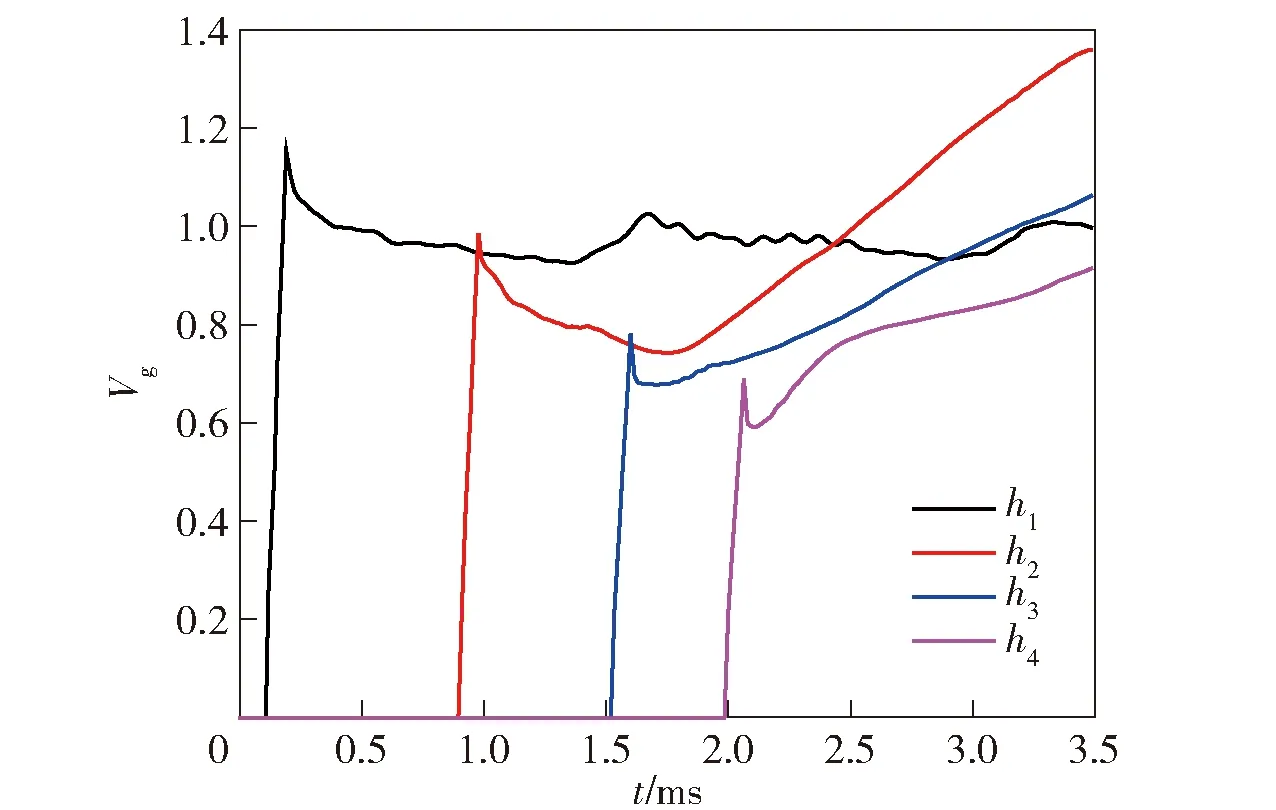
图7 4个观测点处爆轰产物相对体积Fig.7 Relative volumes of detonation products at four fixed points

图8为本文数值模拟计算得到的4个观测点处迭代变量β的变化曲线。由图8可知，在整个计算过程中β始终在0～1的范围内变化，β变化范围较小。此外，整个计算过程中β光滑过渡，有助于快速收敛。本文计算中，每个网格的迭代次数不超过3次，证明本文所采用迭代算法是高效、可行的。因此，采用β作为迭代变量有利于减少迭代次数，提高计算效率。

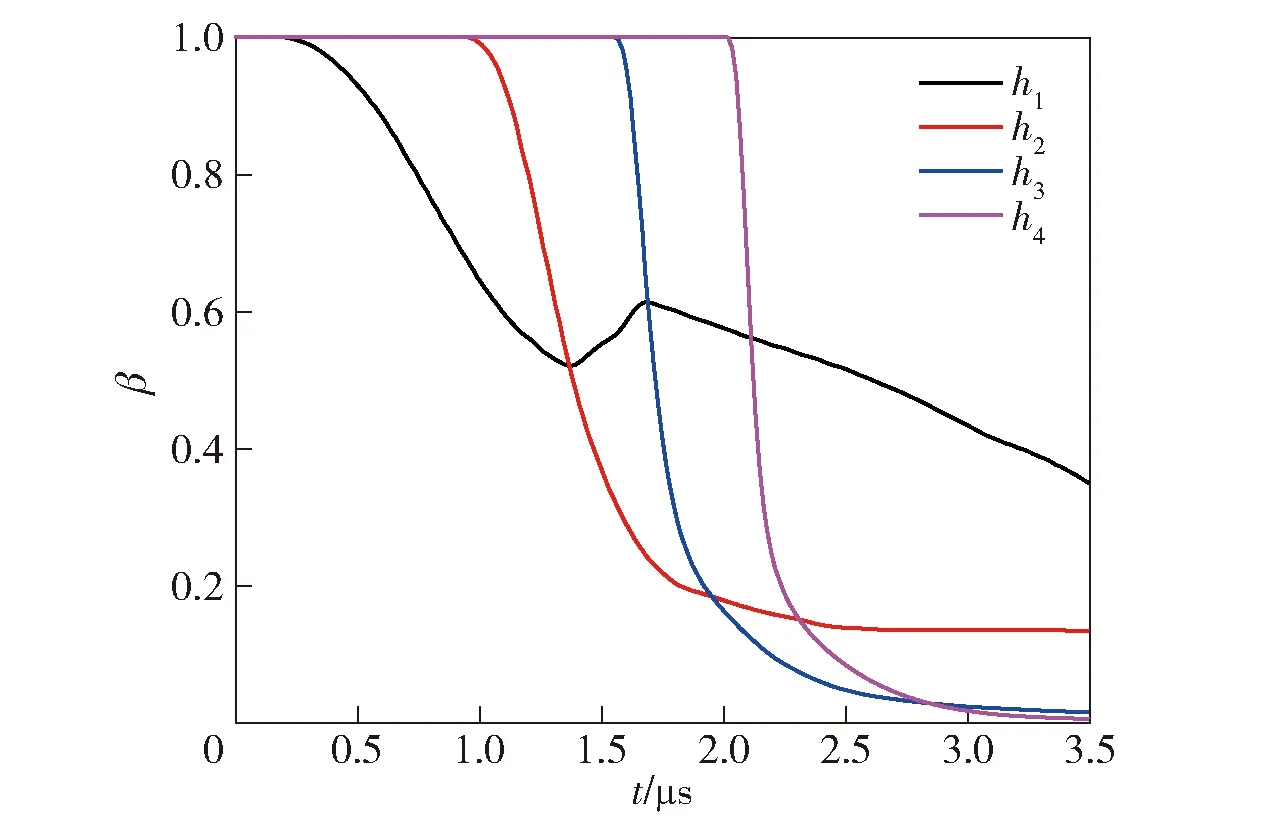
图8 4个观测点处迭代变量βFig.8 Iterative variables β at four fixed points

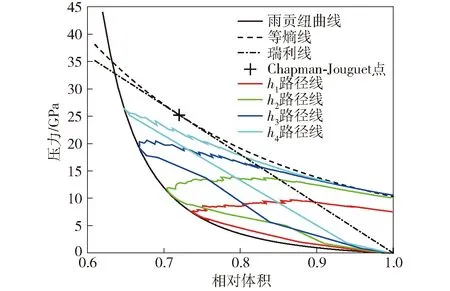
图9 4个观测点处的压力与相对体积路径Fig.9 p-V paths at four fixed points

此外，自定义模型可以输出更多的流场信息，有助于进一步观察反应区结构，并对实验设计提供指导。为了更详细地描述冲击起爆过程，可以对图9中4个观测点在p-V图上的路径与雨贡纽曲线和等熵线的关系进行分析。以h1处观测点为例，冲击波入射到炸药中，压力从0 GPa升高到7.5 GPa，落在雨贡纽曲线；随后，炸药开始反应，反应分数逐渐增加，(V，p)点逐渐向等熵线靠近；当相对体积为1.0(图10中“+”)时，对应的反应分数为0.64，随后继续膨胀。其他3条曲线的过程类似。值得注意的是，h4处观测点反应分数达到1时，相对体积为0.95. 而Chapman-Jouguet点对应的相对体积为0.72，所以在h4处仍未建立稳定爆轰。因此，如果想在实验中记录到稳定爆轰的状态，可以适当增加最后一个传感器位置到边界的距离。

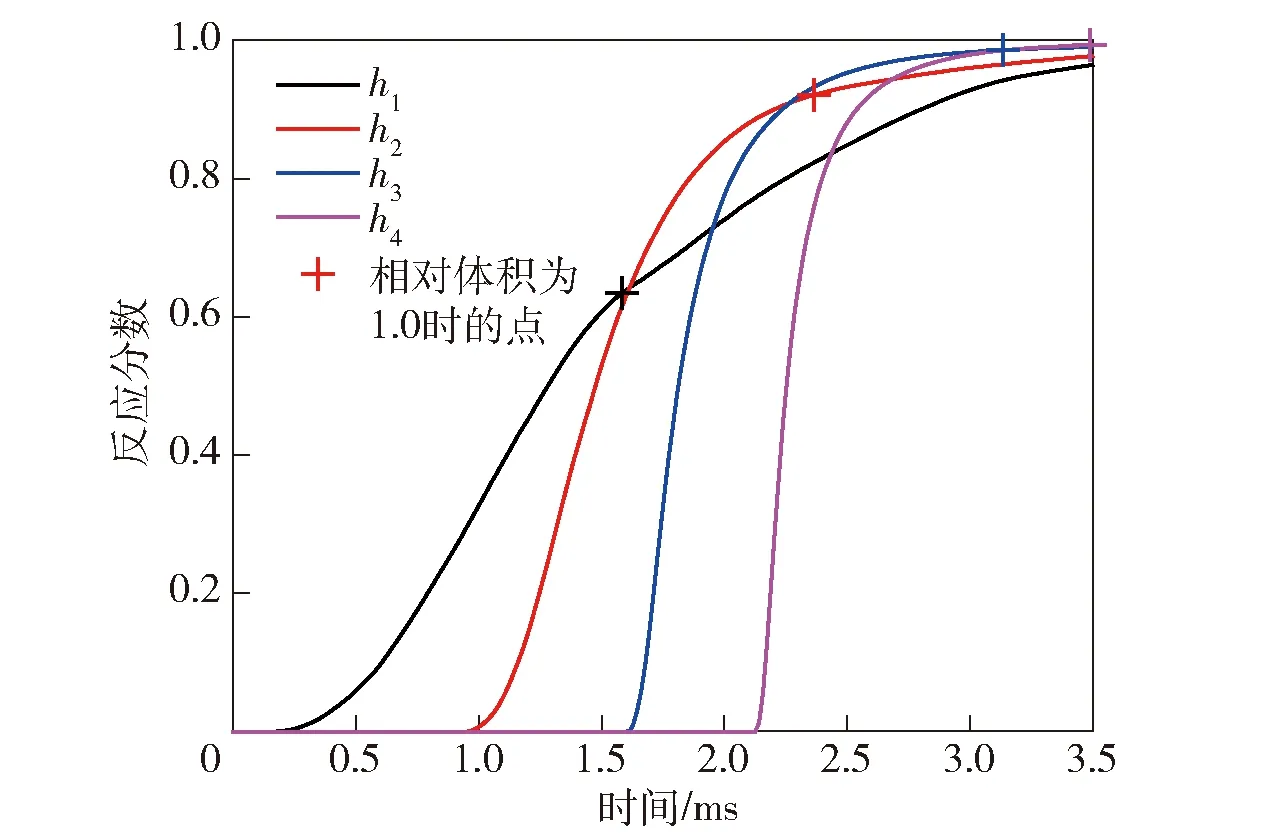
图10 4个观测点处反应分数Fig.10 Reaction fractions at four fixed points

3 结论

本文通过自定义状态方程的形式将改进的点火增长模型嵌入LS-DYNA软件，对DNAN基含铝熔注炸药冲击起爆进行了数值模拟，并与实验值进行了对比。得出以下结论：

1)计算得到的4个传感器位置处的冲击波到达时间与实验值相差不超过0.2 μs，改进的点火增长模型能够很好地描述炸药的冲击起爆过程。

2)以β作为迭代变量的压力更新算法计算效率高。本文计算中，每个网格的迭代次数不超过3次。

3)将Lagrange位置处的压力与相对体积路径线与未反应炸药的雨贡纽曲线、爆轰产物的等熵线画在一张图上有助于理解炸药在冲击起爆过程中的状态变化、判断该Lagrange位置处的炸药是否达到稳定爆轰和深化对冲击起爆过程的认识。