高强铝合金加筋薄壁梁板元相互作用研究

牛瑞涛，刘 伟，高维成

（哈尔滨工业大学 航天学院，哈尔滨150001）

0 引 言

现代结构工程发展的一个显著标志为薄壁结构在建筑、能源、海洋工程及航空、航天等工业领域的广泛应用[1]。作为一种典型的薄壁结构，在弯曲和剪切载荷共同作用下薄壁梁的静力失效主要是由组成板元的面外屈曲造成的。

加筋薄壁梁结构设计灵活，结构承载力影响因素较多，在已有的薄壁梁静力承载特性试验研究很少[2-7]的情况下，如何提出得到公认的简单有效薄壁梁承载力计算方法一直是结构工程领域的难点问题。同时，因为薄壁梁由多个局部板元组成，所以各个局部板元之间的相互作用以及局部板元与整体结构之间的相互作用也是结构分析必须考虑的问题[8]，但是目前尚未出现考虑屈曲相互作用的薄壁梁结构设计方法。此外，随着高强结构材料的快速发展以及工程结构设计要求的不断提高，由各种高强材料制造而成的承力工程结构越来越多[9]，但是相关的结构设计准则尚未建立，目前重要的高强结构设计仍须进行试验验证。

基于以上问题，本文进行了高强铝合金加筋薄壁梁的试验与仿真研究，进一步丰富了薄壁梁承载特性数据；试验发现了一种新的结构承载力相互作用，即由加强筋隔开的不同板元之间同样存在相互作用；建立了能够与试验数据相互验证的有限元模型，并利用此仿真模型研究了材料屈服强度对新发现的板元承载力相互作用的影响。

1 试验设计

所有试验件均为对高强铝合金铝锭进行整体铣削机加工而成的加筋“[”形薄壁梁，沿纵向试验件被横向加强筋分割为多个子段，试验件设计参考某实际工程主承力梁特定位置的剖面结构特征。为了研究跨中腹板开口设计对结构承载能力的影响，根据中跨腹板几何特性的不同试验件共有三种，第一种试验件为基础试验件，记为梁TA；与梁TA相比第二种试验件跨中三段腹板上设计有纵向止裂筋，记为梁TB；与梁TB相比，第三种试验件在中跨腹板设计方形大开口，并对开口周边矩形区域进行单侧加厚补强，记为梁TC，三种梁试验件设计如图1所示。

图1 梁试验件分类Fig.1 Classification of test beams

试验装置如图2所示。采用两个作动筒同时加载以得到满足试验要求的目标载荷F0。为消除有害的扭矩作用，每两个试验件（编号分别为A和B）为一组进行背对背试验加载，在梁两端通过连接板进行螺栓连接以形成闭合剖面。两根梁之间保持一定的间距以彼此独立承载。每种试验件各进行一组静力加载试验。试验件的承载响应通过应变片进行监测，对于每个测点板元的内外表面均布置应变片。确定合理的加载步逐级加载直至试件破坏为止。

图2 整体试验承载方案Fig.2 Test setup

2 试验结果与分析

2.1 试验件极限载荷

根据试验方案完成试验测试，试验件的极限载荷如表1所示。根据表1中所列出的试验件极限载荷，可以得到以下结论：

（1）梁TA与梁TB的区别为梁TB有止裂筋而梁TA没有，两种试验件极限载荷基本相同，表明止裂筋不影响试验件极限承载力；

表1 试验件极限载荷Tab.1 Limit capacity of test beams

（2）梁TC极限载荷比TA与TB类提高了约13%。由于三种试验件的加载方式、边界约束和结构材料完全相同，因此不同试验件承载能力的差异由梁腹板几何参数的变化引起。由于止裂筋已经被证明不影响结构承载能力，可以认为，与其它试验件相比梁TC承载能力更高是由跨中腹板的开口补强设计引起的，中跨腹板的开口补强设计有效提高了结构极限承载力。

2.2 试验件破坏模式

图3 试验件破坏变形Fig.3 Collapse deformation of test beams

图3所示为三种试验件的破坏变形图。达到极限荷载时，所有试验件均在固定端侧窄梁段受压翼缘发生显著的局部塑性弯曲变形。可以认为此受压翼缘为试验件承载薄弱部位，记为屈曲翼缘。随着试验载荷的增加，屈曲翼缘发生局部破坏而使得整体试验件失效。通过不同试验件破坏变形的对比可以发现一个现象：6个试验件中，5个试验件屈曲翼缘发生向内塑性弯曲变形，而与之相反，开口补强试验件TC-B的屈曲翼缘发生向外塑性弯曲变形。

图4所示为不同试验件屈曲翼缘中心测点的载荷-应变曲线，据此可以进一步分析屈曲翼缘塑性弯曲变形的形成机理。当载荷较小时，测点内外表面应变差值很小，可以认为此时屈曲翼缘无弯曲变形。5个试验件屈曲翼缘均发生向内弯曲变形，其载荷-应变曲线具有明显的共性规律，当接近极限载荷时，载荷-应变曲线的斜率变化突然加快，表明屈曲翼缘在临近失效时发生了明显的刚度弱化。而梁TC-B屈曲翼缘发生向外弯曲变形，其载荷-应变曲线明显不同，随着载荷的增加，载荷应变曲线发生了一次斜率突变，突变后的曲线斜率仍能进一步保持稳定。同时，虽然根据载荷-应变曲线进行屈曲载荷的精确判定存在很大的困难，但是根据屈曲前后的应变值仍可以定性地判定出：屈曲翼缘发生弹性屈曲而非塑性屈曲。本研究直观地认为：梁TC-B明显不同的破坏模式与其更高的极限载荷之间具有某种关联，并值得进行进一步的深入研究。

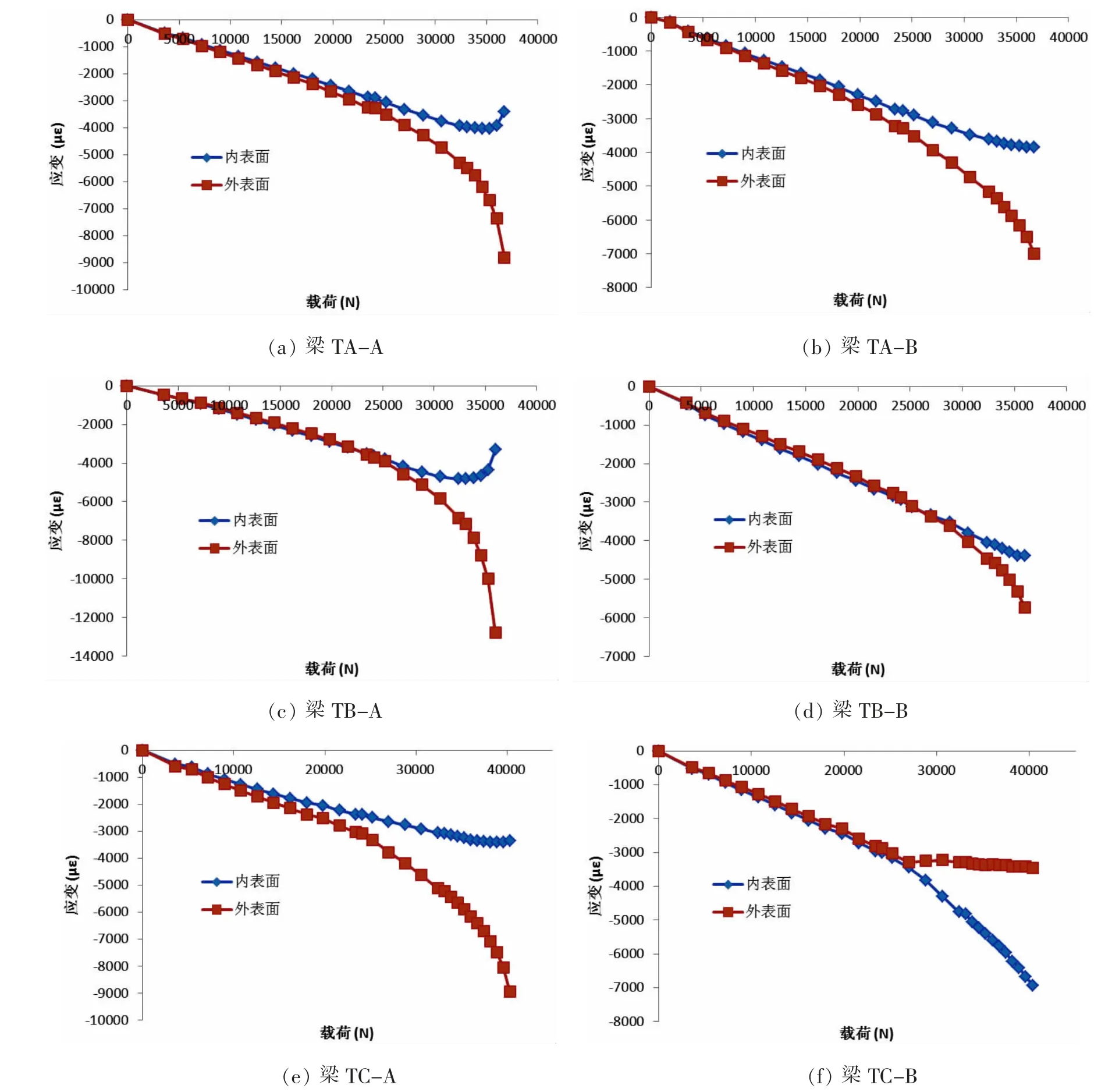
图4 试验件屈曲翼缘中心测点的载荷-应变曲线Fig.4 Load-strain curves of buckling flange

2.3 板元承载力相互作用

从结构形式上看，薄壁梁试验件为由翼缘、腹板和加强筋组成的组合结构。在这里着重指出本试验研究的一个显著成果：通过不同试验件极限荷载与破坏模式的综合对比分析，在复杂薄壁结构强度研究领域发现了一种新的局部板元相互作用。

对于不同试验件，虽然结构破坏均由屈曲翼缘的局部屈曲所造成，但是开口补强试验件的极限荷载比无开口试验件提高了约13%。之前已经指出，这种结构极限载荷的差异是由跨中腹板结构参数的变化造成的，与无开口试验件相比，开口补强试验件的跨中腹板上有矩形大开口并在开口周边区域进行了加厚补强。但是需要注意，跨中腹板的开口补强提高了相邻梁段翼缘的局部承载力，这种现象不符合传统的结构强度认知。传统的板元局部承载力理论认为：当板元发生局部屈曲时，加强筋能够起到隔波作用，因此翼缘和腹板被加强筋分割为不同单元，将各个翼缘和腹板单元视为计算对象分别进行计算，只有相邻板元可以影响计算板元的局部承载力，且其影响表现在计算板元边界的面外位移约束和旋转约束。按照传统理论，本研究试验件的跨中腹板与相邻梁段的屈曲翼缘不存在相互作用。传统理论与本文试验结果相矛盾，因此，本研究首次通过试验验证了传统的板元局部承载力计算方法的局限性。从更为一般的意义上讲，本研究所发现的板元承载力相互作用可以表述为，在复杂组合结构中，某局部构件的承载力可以受到整体结构中与其不相邻局部构件的影响。本发现的工程实际意义在于结构设计理念的突破：对于实际的复杂组合工程结构，进行局部构件承载力计算时，若不考虑整体结构影响，则可能出现严重错误。

3 薄壁梁数值模拟

3.1 有限元模型

本研究选用有限元前处理软件MSC Patran进行薄壁构件的仿真建模。为了节约计算成本，仅选取靠近固定端一侧的主要梁段部分进行建模分析。根据试验结果可知，止裂筋对试验件承载能力的影响可以忽略不计，因此本研究在进行数值建模时不添加止裂筋，从而得到两种几何仿真模型，一种腹板无开口模型以梁TA为原型，记为TA-FEM；另外一种腹板开口补强模型与TC类试验件相比无止裂筋，记为TC-FEM。在固定端约束梁端“[”形横截面所有6个方向的自由度。加载端侧腹板外边缘被约束面外平移自由度并施加均匀的面内剪力流。选用CQUAD4壳单元进行几何模型的有限元离散。由于试验件的开口补强采取的是对开口周边矩形区域的单侧均匀加厚，因而矩形补强区的中面与腹板中面相偏离。为了在有限元模型中引入这种中面的互相偏离，本研究采取了这样一种手段：在开口补强区域的中面位置建立其有限单元，此时矩形开口补强区的4条外边与腹板非补强区的4条内边的边节点的面内坐标相同，然而由于面外坐标的不同而互相分离，对于每一对相应节点创建Rigid（Fixed）多点约束单元，以实现开口补强区与腹板非补强区的连接。所得到的腹板无开口有限元模型和腹板开口有限元模型如图5所示。

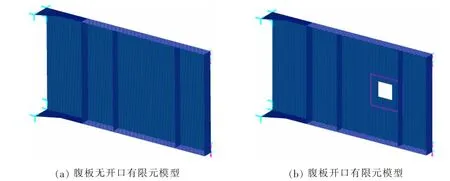
图5 两种有限元模型Fig.5 Two finite element models created

3.2 数值模拟与试验结果对比

本研究利用MSC Nastran的SOL106求解器，进行基于大位移与小应变假定的结构非线性分析。本节从试验件的破坏模式、极限载荷与整体承载响应三个方面进行了数值模拟与试验结果的对比分析。首先，图6所示为两种模型的破坏模式，屈曲翼缘上的von Mises应变值远大于模型其它区域，可以认为有限元模型的结构破坏是由屈曲翼缘的局部破坏造成的，这与试验结果是一致的。腹板无开口有限元模型屈曲翼缘的破坏变形为向内弯曲变形，这与试验结果也是一致的。腹板开口补强有限元模型屈曲翼缘的破坏变形为向外弯曲变形，这与TC-B试验件的试验结果相一致。其次，表2所示为两种有限元模型与相应的试验件的极限荷载对比，仿真值略小于试验值，但最大误差的绝对值为6.0%，可以认为仿真值与试验值吻合良好。最后，在加载过程中结构会发生屈曲，这使得结构的承载响应随着载荷的增加会出现明显的非线性变化。本研究选取屈曲翼缘中心的载荷-应变曲线（如图7所示）来表征结构的承载响应。从图中可以看出，在加载前期的线弹性范围内仿真曲线与试验曲线基本相等，随着载荷的增加结构发生屈曲后，仿真曲线与试验曲线的变化趋势仍然保持一致，可以认为仿真计算结果能够反映试验件的整体承载响应变化。综上所述，本研究所采用的有限元模型能够很好地模拟试验件的承载特性，可以进一步进行有限元计算以深入探索薄壁梁承载机理。

表2 试验件极限载荷的试验测试值与仿真计算值对比Tab.2 Comparison of limit loads of test beams from experiment and FEA

图6 仿真模型von Mises应变分布图Fig.6 von Mises strain distribution of FE model

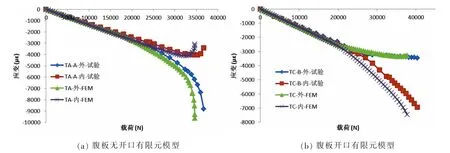
图7 屈曲翼缘中心测点载荷-应变曲线的试验-仿真对比Fig.7 Comparison of load-strain curves of centers of buckling flanges from experiment and FEA

4 材料屈服强度对板元相互作用的影响

对于TA-FEM与TC-FEM，在其它参数不变的情况下，材料屈服强度分别取100、200、300、400、450、500、550 MPa进行非线性有限元分析，不同屈服强度计算得到的极限载荷与破坏模式分别如表3和图8所示。当屈服强度为100 MPa时，两种模型的极限载荷与破坏模式基本一致，结构达到极限荷载时，屈曲翼缘未发生明显弯曲变形，屈曲翼缘应变绝对值远高于结构其它区域。可以认为，当材料屈服强度很低时，试验中所发现的板元相互作用现象消失，可以利用传统结构理论进行承载力计算。当屈服强度增大到200 MPa时，虽然两种模型极限载荷的差异依然很小（3.2%），但是结构的破坏模式发生了突变，TC-FEM屈曲翼缘变为向外弯曲变形，表明屈服强度的变化引起了结构受力模式的改变，发生板元相互作用。随着屈服强度的进一步增加，破坏模式保持不变，但是两种模型极限载荷的差异越来越大且TC-FEM的极限载荷始终高于TA-FEM，从σ0.7=200 MPa时的3.2%逐渐增大到σ0.7=550 MPa时的20.7%，可以预计当屈服强度σ0.7继续增大时两种模型极限载荷的差异还会进一步提高。通过以上分析可以看出，当薄壁梁其它参数不变时，材料屈服强度可以显著影响结构极限载荷与破坏模式。因此，对由新型高强材料制成的薄壁梁进行强度校核时，直接套用普通低强材料的结构承载力计算方法是不合适的，可能会得到偏危险的承载力预测值。这也说明，采用新材料进行结构设计时，必须进行相应的结构承载力计算方法研究。

表3 不同屈服强度所得到的两种仿真模型极限载荷Tab.3 Limit load of two FE models of different yield strength

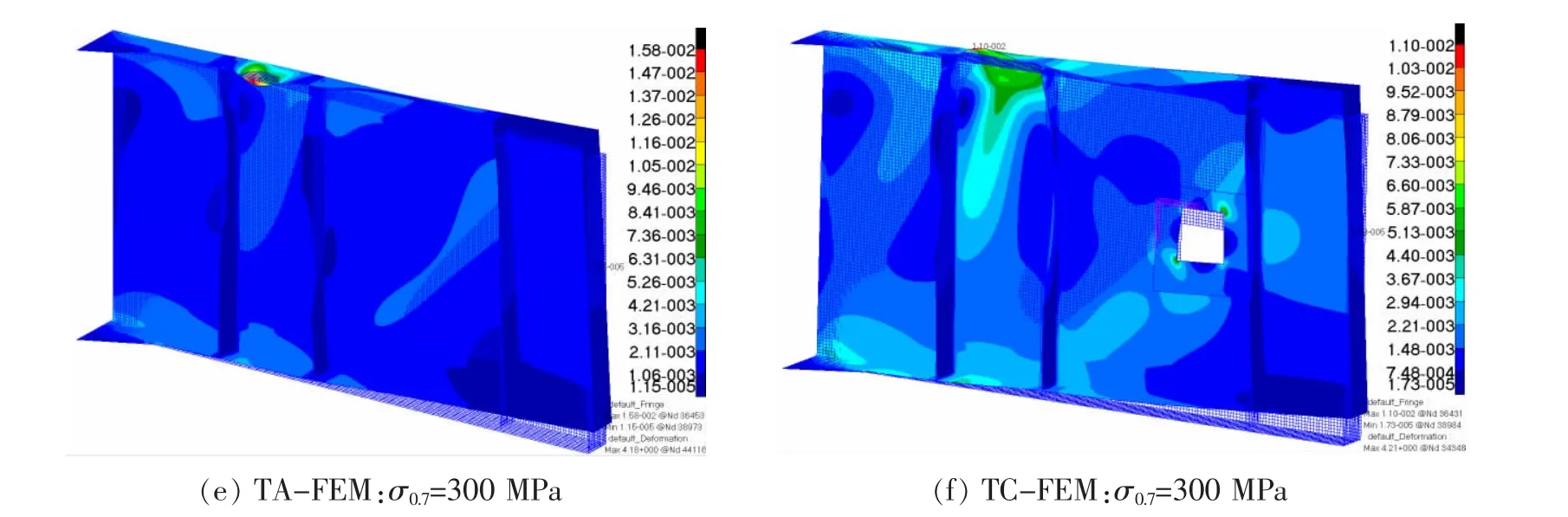
图8 不同屈服强度下两种模型的破坏应变分布图Fig.8 Collapse strain distribution of two models at different yield strength

5 结 论

本文利用试验和仿真方法进行了高强铝合金加筋薄壁梁的承载特性研究，所得主要结论如下：

（1）本研究试验件的破坏均由翼缘的局部破坏导致，已有文献中薄壁梁试验件失效也大多由翼缘失效引起。因此，翼缘是薄壁梁结构设计的关键部位；

（2）不同试验件试验结果的对比表明，腹板开口补强设计显著提高了试验件承载能力。本研究的薄壁梁开口补强设计可以为相关的板元开口补强设计提供借鉴；

（3）试验发现了一种新的薄壁梁板元承载力相互作用：局部板元的变化可以引起不相邻板元承载力的显著改变。进行局部板元承载力计算时需要考虑整体结构的影响；

（4）提出了与试验结果吻合良好的非线性有限元分析模型，利用此仿真模型可以进行更深入的薄壁梁承载机理分析；

（5）不同材料屈服强度所得到的两种仿真模型计算结果的对比表明：屈服强度增大到一定程度才会发生板元承载力相互作用，材料屈服强度越高，相互作用引起的板元承载力变化越大。因此，进行高强材料薄壁梁设计方法的研究很有意义。

致谢：作者感谢哈尔滨工业大学土木工学院周广春教授修改建议，并致谢试验中上海飞机设计研究院给予的帮助。