双向应力场中表面裂纹应力强度因子的权函数法

袁奎霖，周忠华，赵 峰，洪 明

（大连理工大学 船舶工程学院 工业装备结构分析国家重点实验室，辽宁 大连116024）

0 引 言

船舶等大型焊接结构在交变外载荷作用下，在应力集中较严重的焊趾部位极易萌生多处微裂纹,随着微裂纹生长与合体形成近似于半椭圆形状的表面裂纹[1]。表面裂纹沿板厚和板宽方向不断扩展，直至贯穿钢板形成穿透型裂纹甚至引发断裂破坏。为了保证结构服役安全性，表面裂纹尖端应力强度因子的计算是损伤容限设计中极其重要的一部分。

对于半椭圆表面裂纹应力强度因子的计算，已有国内外学者对此进行了大量研究，其中有限元法是最常用的方法之一。Newman和Raju[2-3]通过建立三维有限元模型对远端拉伸载荷和弯矩作用下的有限厚度平板表面裂纹应力强度因子进行了分析，并且总结了相应的经验公式。Bowness等[4]针对T型接头中的表面裂纹，结合三维有限元分析，给出了考虑焊趾处应力集中影响的应力强度因子放大系数Mk的计算公式。Shiratori等[5]基于线性叠加原理将远场载荷与结构局部应力集中的影响转化为裂纹面上的近场应力载荷，分别计算了在0～3次多项式表达的沿板厚方向变化应力场作用下平板表面裂纹应力强度因子。然而，实际焊接结构由于受形状复杂性和焊接残余应力的影响，焊趾处应力载荷往往沿板宽和板厚方向同时变化（如图1所示），并且需要高次多项式进行拟合[6]，这对应力强度因子的有限元计算造成了很大困难。

与有限元法相比，权函数法是求解复杂应力场作用下裂纹应力强度因子的高效计算方法。应力强度因子的权函数法最早由Bueckner[7]和Rice[8]提出，并证明了权函数是裂纹体的几何特性，一旦确定便可用来计算任意载荷分布下的应力强度因子，所需计算仅是一个与裂纹面应力乘积的积分。Glinka等[9-10]基于权函数与裂纹开口位移之间的关系，提出了适用于穿透型裂纹和半椭圆表面裂纹的一维权函数统一形式，并被美国石油协会规范API-579[11]所采用。Wang等[12-13]在已有统一权函数基础上，通过有限元计算和Shiratori[5]的数据，分别发展了小半长比（a/c=0.05～1.0）和大半长比（a/c=0.6～2.0）的平板表面裂纹权函数。然而，上述权函数仅适用于裂纹面上应力载荷单向变化（即沿板厚方向）的情况，对于实际工程中遇到的双向变化应力情况则难以直接应用。针对这一问题，Wang和Glinka[14]基于无限体中裂纹面上集中力载荷诱导的应力强度因子解析解的特性，提出了一种任意载荷作用下椭圆形埋藏裂纹的二维权函数统一形式。Jin和Wang[15]考虑了有限板厚的边界效应，进一步提出了平板表面裂纹的二维统一权函数，但遗憾的是仍只验证了沿板厚方向的最高三次分布应力。此外，现有权函数[11-15]的裂纹深度比适用范围主要集中在a/T=0.2～0.8,而对于焊接接头的初始表面裂纹尺寸（例如裂纹初始深度a0=0.5 mm，板厚T=20 mm[16]，a/T=0.025）仍需要改进。

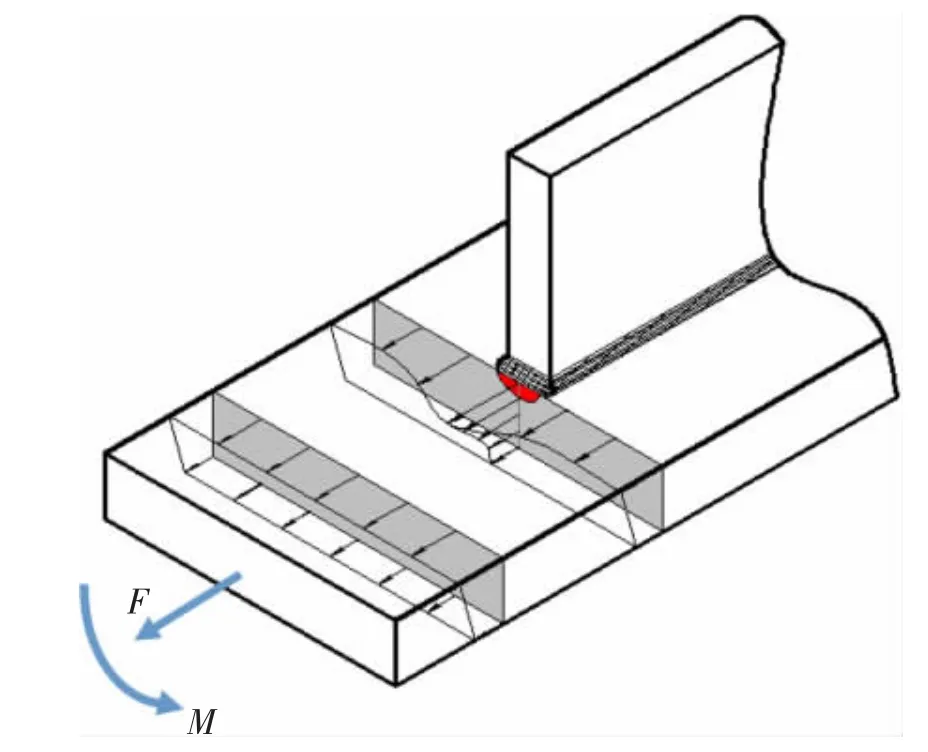
图1 焊趾表面裂纹附近应力场Fig.1 2-D stress field near weld toe

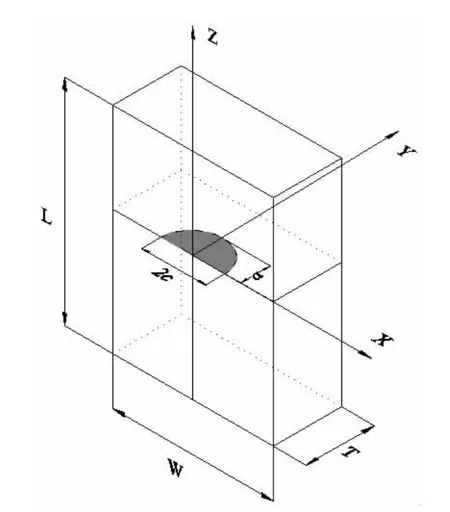
图2 有限厚度平板半椭圆表面裂纹形状与坐标系Fig.2 Geometry and coordinate system for semi-elliptical surface crack in finite thickness plate

本文基于Wang等[14-15]提出的二维权函数统一形式，通过创建裂纹半长比a/c=0.05～1.0，裂纹深度比a/T=0.01～0.8的平板表面裂纹三维有限元模型，分别计算了裂纹最深点和表面点的应力强度因子并将其作为参考解，提出一组裂纹形状适用范围更广的表面裂纹二维权函数。在此基础上，通过在裂纹面上施加两组不同的最高阶次为六次的复杂应力载荷进行计算，与有限元结果对比，验证了本文所提出的权函数的准确性。

1 二维权函数统一形式

基于叠加原理，理论上采用权函数法可以计算任意载荷条件下的应力强度因子。对于一维贯穿型裂纹，基于权函数法的裂纹应力强度因子计算公式如下：

式中：x为裂纹面坐标，a为裂纹长度，σ（x）为无裂纹体假想裂纹处应力分布，m（x,a）为权函数。m（x,a）表示作用于x点处的单位集中力载荷诱导的裂纹尖端应力强度因子。Glinka和Shen[9-10]指出，对于一维和二维裂纹，权函数可由（2）式的统一形式表示：

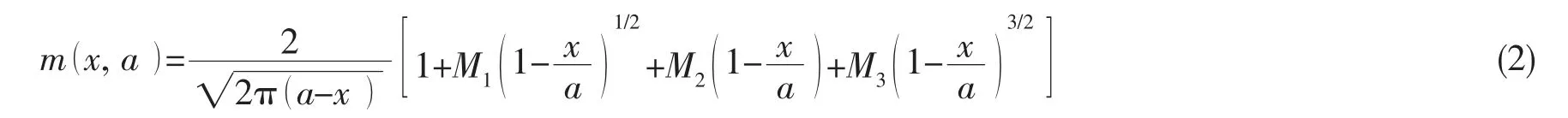
式中：M1、M2和M3为权函数系数。需指出，对于半椭圆表面裂纹，（2）式仅适用于应力分布沿板厚单向变化的情况。

对于双向变化应力场中的二维裂纹，应力强度因子可由权函数m（x,y;P′）和应力分布σ（x,y）在裂纹面全域S上的双重积分计算得到：

可知，m（x,y;P′）表示（x,y）点处的单位集中力载荷在裂纹前缘P′点处诱导的应力强度因子。Wang等[14-15]对于图2所示平板半椭圆表面裂纹提出了二维权函数统一形式：

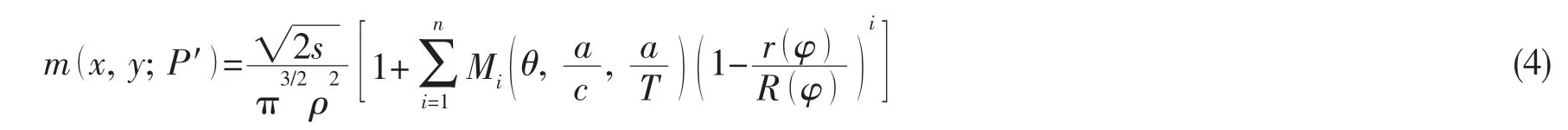
Ghajar等[17]研究表明，当n=1时即如（5）式所示的权函数统一形式对于不同形状的半椭圆表面裂纹都具有良好的计算精度：

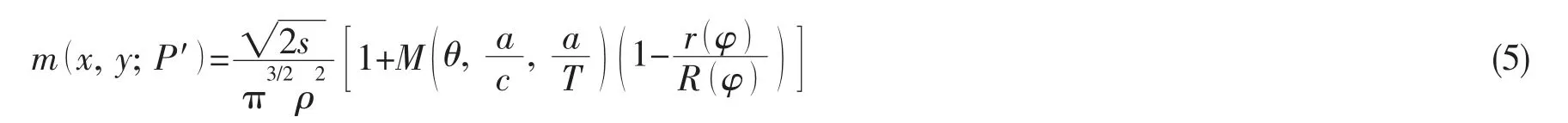
图3 半椭圆表面裂纹各参数示意图Fig.3 Parameters for semi-elliptical surface crack

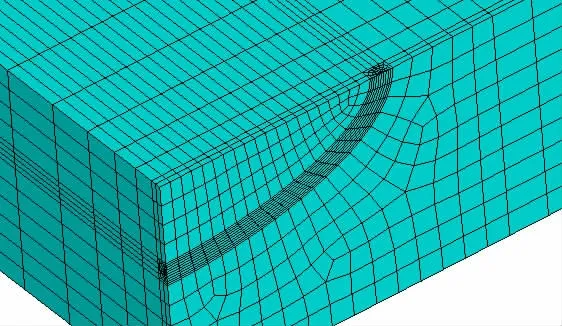
图4 表面裂纹有限元模型Fig.4 Typical FE model for surface crack

式中：s是载荷作用点P到裂纹前缘的最短距离，ρ是载荷作用点P到应力强度因子计算点P′的距离，θ代表P′在裂纹前缘的位置，r与φ为载荷作用点P的极坐标（见图3）。求解权函数中的未知系数M，一般需要已知某种载荷下的一系列高精度应力强度因子作为参考解，可采用文献中已知数据或进行有限元计算得到。

2 平板表面裂纹有限元分析

由于现有文献中关于浅表面裂纹（a/T＜0.2）的应力强度因子数据鲜有报道，本文自行创建了裂纹半长比a/c=0.05、0.1、0.2、0.4、0.6、0.8和1.0，裂纹深度比a/T=0.01、0.05、0.1、0.2、0.4、0.6和0.8，共49个平板表面裂纹三维有限元模型。如图4所示，采用对称边界条件创建了1/4裂纹模型，载荷加载方式为在裂纹面上直接施加应力分布载荷，材料模型为线弹性体，杨式模量E=2.06E5 MPa，泊松比υ=0.3。有限元软件为ANSYS 16.0，采用的单元为20节点的SOLID 186高阶体单元，其中裂尖单元采用奇异单元处理，应力强度因子计算方法为位移外插法。

为了验证有限元模型的准确性，在裂纹面上施加如下四种应力场：

式中：σ0为名义应力，a表示裂纹深度，取n=0,1,2,3。求得的应力强度因子按（7）式进行归一化处理：

式中：F为边界效应修正因子，Q为第二类椭圆积分的近似解。参考Shiratori[5]的结果，对最深点和表面点的边界修正因子F的计算结果进行对比，所有结果的误差均在5%以内，部分整理结果如表1所示。验证结果表明本文创建的表面裂纹有限元模型具有良好的计算精度，并认为浅表面裂纹（a/T＜0.2）的应力强度因子有限元结果可作为后续的参考解。

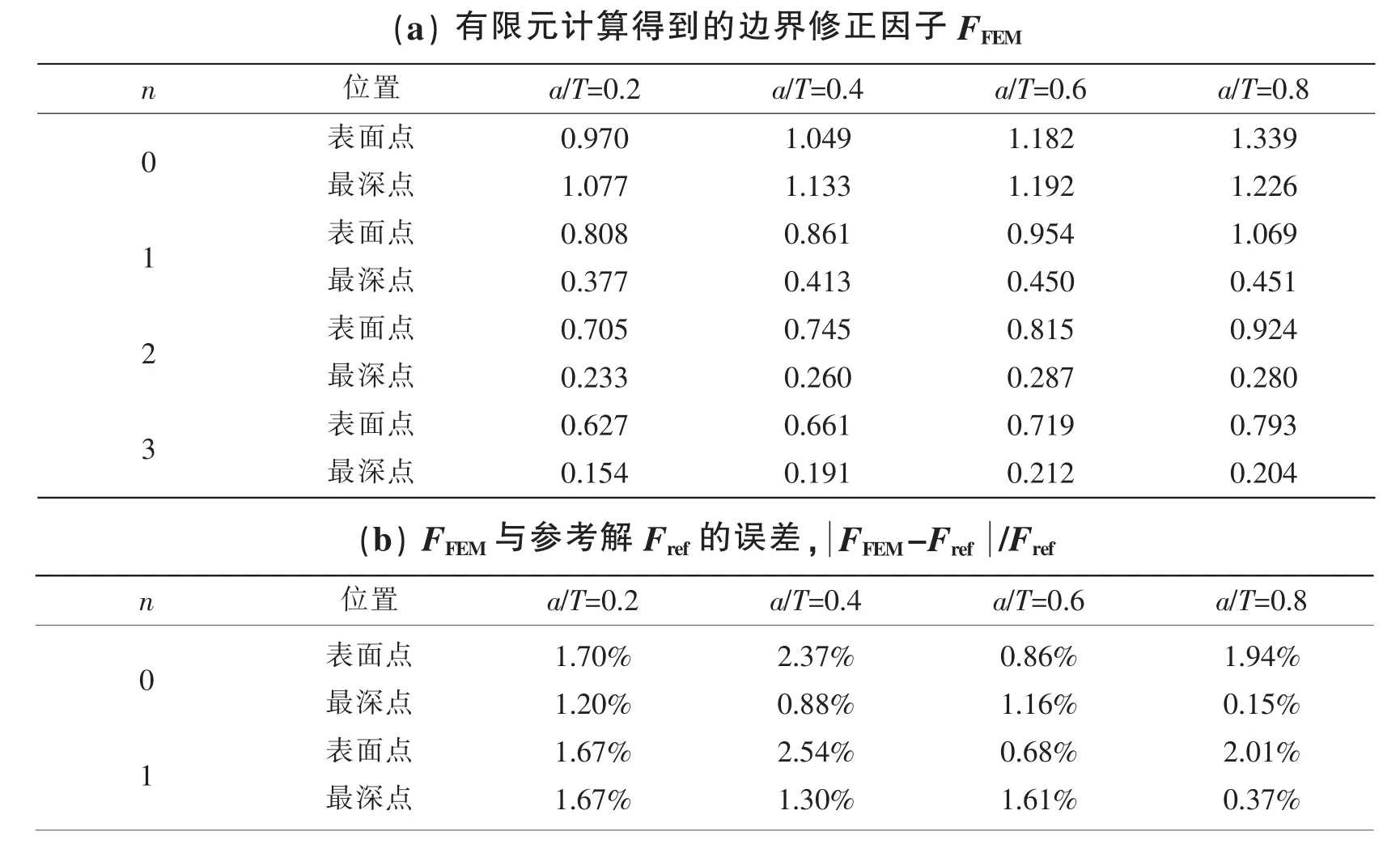
表1 有限元计算得到的边界修正因子F与Shiratori参考解[5]对比，a/c=0.6Tab.1 Comparison of boundary correction factors from present FEM calculation and Shiratori et al[5],a/c=0.6

续表1（b）

3 权函数求解

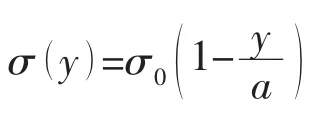
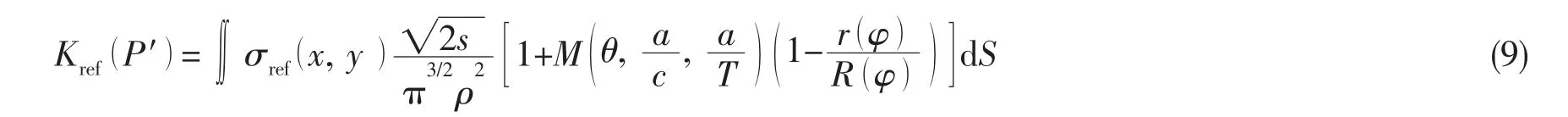
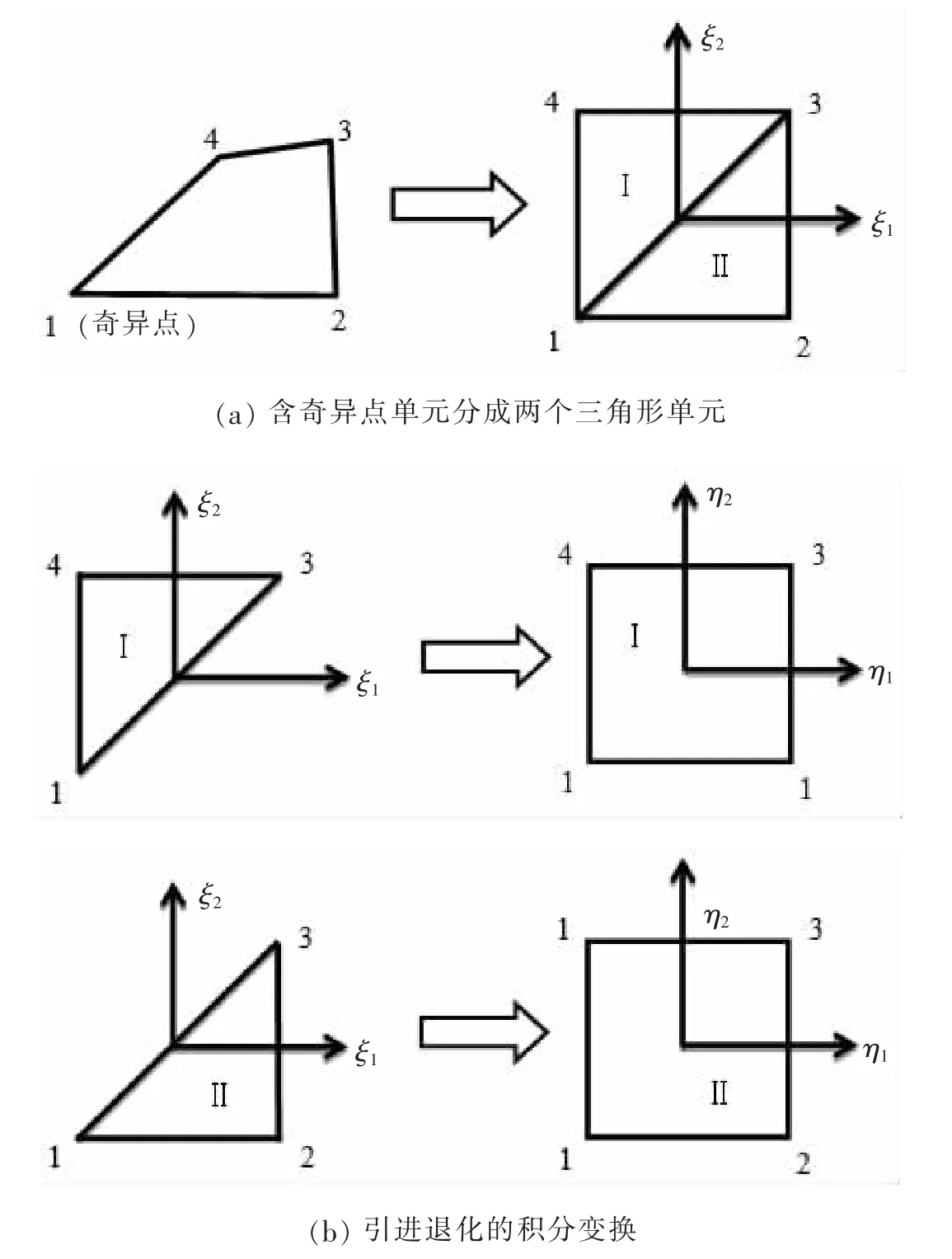
图5 单元子分法示意图Fig.5 Schematic illustration of element subdivision technique

采用上述方法分别对裂纹半宽比a/c=0.05～1.0，裂纹深度比a/T=0.01～0.8的不同形状表面裂纹的表面点和最深点处对应的权函数参数M进行了求解，结果汇总见表2。为了方便工程应用，采用了最小二乘法对表2中的M值进行多项式拟合得到参数公式（详见附录），拟合优度R2均大于0.99。

4 权函数的有效性验证

为了验证权函数的有效性，将由一阶参考载荷得到的权函数扩展应用到高阶载荷的情况，权函数计算得到的高阶载荷下应力强度因子与有限元结果进行对比。

4.1 沿板厚单向变化的应力分布

式中a表示裂纹深度。将（10）式所表达的沿板厚方向变化的线性分布应力和非线性分布应力载荷施加在裂纹面上，计算所得的应力强度因子经归一化后得到边界修正因子F。如图6所示，将有限元法与权函数法的计算结果进行对比，并统计了两者之间的误差（见图7）。除a/T=0.01，a/c=0.8和1.0的高阶应力m=4～6情况，其他裂纹形状的计算误差均在10%以内，满足实际工程需要。需要说明的是，相对误差超过10%的边界修正因子F绝对值很小且均小于0.1，因此并不影响本权函数的适用性。

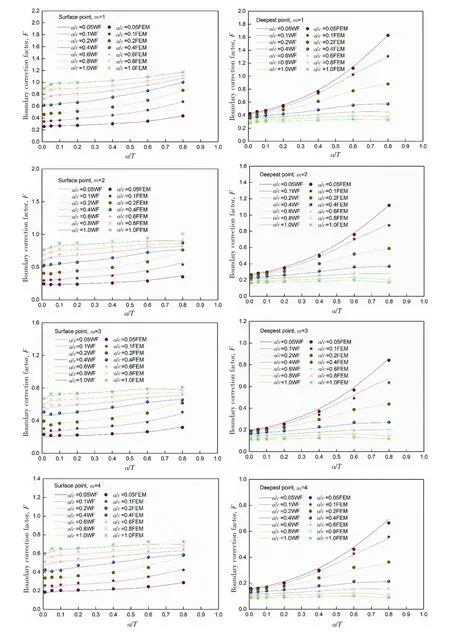
图7 权函数结果与有限元结果之间的误差分析Fig.7 Error analysis of boundary correction factors from weight function method and FEM

4.2 沿板厚和板宽双向变化的应力分布

在船体结构中纵骨端部（如图1所示的焊接接头）是疲劳强度校核的关键节点，焊趾附近的应力分布沿板厚和板宽方向变化。为了模拟上述情形，采用（11）式中所表达的双向变化非线性应力载荷施加在裂纹面上，计算所得的应力强度因子经归一化得到边界修正因子F。如图8所示，将有限元法与权函数法的计算结果进行对比，并统计了两者之间的误差（见图9）。相对误差超过10%的情况出现在a/T=0.01，a/c=1.0的高阶应力m=4～5时，其他裂纹形状的计算误差均在10%以内，可满足实际工程需要。

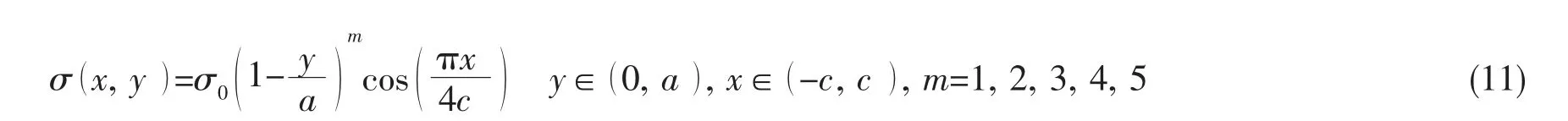
式中，a表示裂纹深度，c表示裂纹半宽。

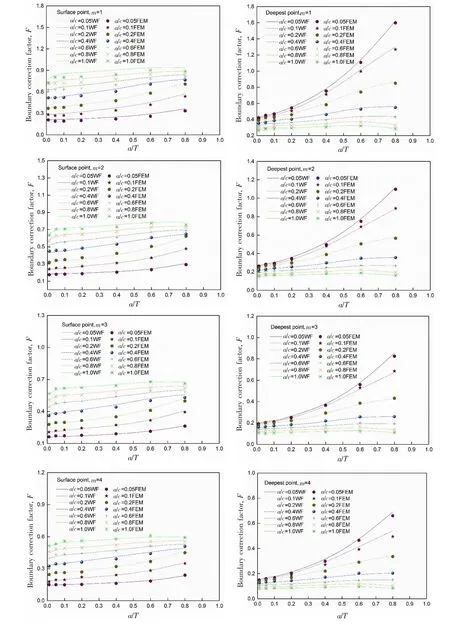
图8 权函数结果与有限元结果对比Fig.8 Comparison of boundary correction factors from weight function and FEM

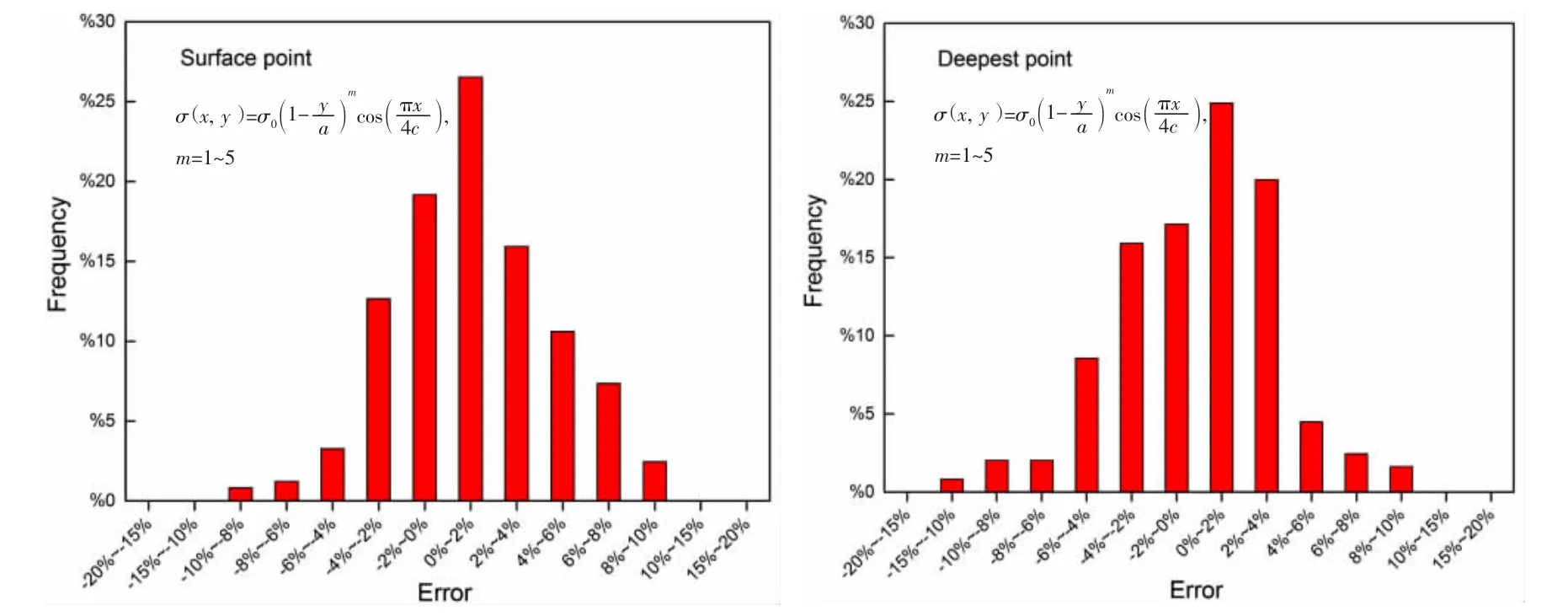
图9 权函数结果与有限元结果之间的误差分析Fig.9 Error analysis of boundary correction factors from weight function method and FEM

5 结 论

本文在Wang等提出的二维权函数统一形式的基础上，采用三维有限元计算得到裂纹半长比a/c=0.05、0.1、0.2、0.4、0.6、0.8和1.0，裂纹深度比a/T=0.01、0.05、0.1、0.2、0.4、0.6和0.8的平板表面裂纹最深点和表面点的应力强度因子作为参考解，得到了裂纹形状适用范围更广的权函数解，并得到以下结论：

（1）由低阶参考载荷得到的权函数可扩展应用到高阶应力分布，本文所提出的权函数可高效准确地求解最高六阶的沿板厚方向和板宽方向变化的复杂应力场作用下的应力强度因子。

（2）对于表面点和最深点，半长比a/c=0.05～1.0，a/T=0.05～0.8之间，权函数结果与有限元结果相比，误差均在10%以内，满足实际工程应用需要。

（3）本文所提出的权函数可应用于考虑结构应力集中、焊接残余应力和焊后表面处理（如喷丸、超声冲击）等影响的实际焊接结构中表面裂纹扩展的数值预报。

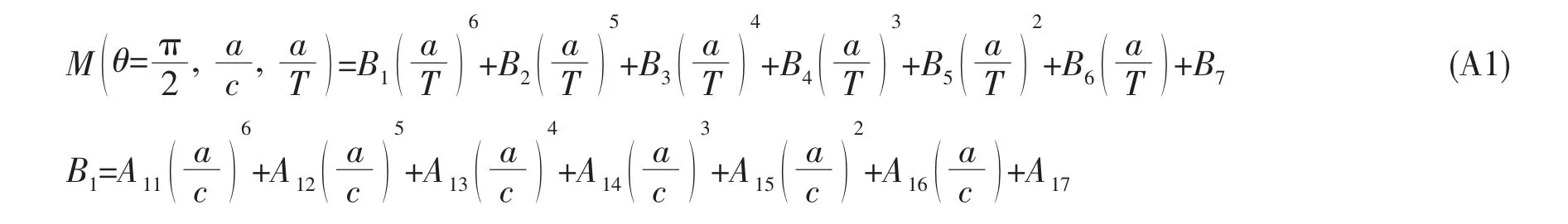
裂纹表面点（θ=0）：