滑动测微计在黄土地区超高层建筑桩基中的应用

彭 伟 娄云雷

（中船勘察设计研究院有限公司，上海 200063）

0 引言

随着超高层建筑的大规模兴建，后注浆灌注桩施工工艺的应用越来越多。为进一步了解桩侧及桩端阻力在荷载作用下的发挥情况，需对桩基进行载荷试验。传统的桩身应力应变测试方法属于点法监测，测点有限，且测得数据只能代表测点处的应变，点位之间的变形量只能推断。另外，传统的测试方法还存在零点漂移、成活率低、受温度影响等缺点，实测结果误差较大[1-3]。

1 滑动测微法的测试原理

1.1 滑动测微计的测量方法

上世纪80年代初，瑞士联邦苏黎世科技大学K.Kovari教授提出线法监测原理，Solexperts AG公司利用这一原理研制出滑动测微计[4]。作为一种高精度便携式应变测量仪器，其主体为标距1 m 两端呈球形的探测头，内置各一个NTC 温度计和LVDT位移计[5]，在测量前后对滑动测微计进行校准，精度可达到1μm[6]。通过桩身埋设的测试元件连续测定整个桩身在各级荷载作用下的应变量，根据桩的荷载传递原理，可以得到桩身应力、抗压测摩阻力、桩端阻力、桩土间相对位移等参数沿桩身连续分布的曲线。

在桩基内力试验过程中，在桩身预埋PVC 套管，管内以1 m 的间距设置环形量测标记，形成测微管。环形量测标记的金属环内槽呈锥面，探头两端呈球面，测标和探头接触面只取锥面和球面的一部分，锥面和球面的极精准特性保证了滑动测微计的高精度测量结果，球锥定位原理见图1。测试时只需将导杆旋转45°，探头由量测位置转换到滑动位置便可在测微管中滑动。探头通过两个测标时将其张紧，探头中的线性位移传感器采集数据（平均温度及测标间距）并传输到控制器中读出，两测标之间的位移便可利用滑动测微计依次测取，滑动测微计工作原理见图2。

图1 球锥定位原理

1.2 测试数据分析及计算

桩身轴向应变采用载荷试验进行，为保证测试精度，每级荷载加载前上下各测定一次每根测管的初始数据，荷载稳定后测定相应读数，其差值乘以标定系数即为各级荷载下每一测段的应变量。将试桩内埋设的两根测管所获得的各水平面数据进行平均，从而得到桩身轴向应变曲线。

（1）桩断面修正

为使计算结果更可靠，成桩前需测定钻孔孔径沿深度的变化曲线，对实测应变进行断面修正，断面修正完成后需用拟合法对应变曲线进行平滑处理。

式中：ki——断面修正系数；

di——相应段实测钻孔孔径，m；

D——钻孔平均直径，m。

（2）平均静弹性模量计算

平均静弹性模量：

式中：Es——桩身平均弹性模量，GPa；

P——桩顶垂直荷载，k N；

A——桩身平均截面积，m2；

ε0——桩身应变，10-6。

根据各级荷载下的桩顶回归应变曲线，便可计算弹性模量随应变量级的变化规律，一般可用线性方程表达：

式中：εi为任意断面处应变量，计算轴向力和摩阻力时采用不同的弹性模量值。（3）轴向力及摩擦力的计算桩身轴向力：

侧阻力：

式中：Ni——任意界面处的轴向力，k N；

fi——桩身i测段处的单位摩阻力，kPa；

L——测段长度，取1 m。

2 试验基本情况

2.1 工程概况

陕西某地新建一超高层，主体建筑为一幢62层塔楼，总高度369 m，地下三层，埋深-16.5 m。塔楼基底压力为1360 kPa，由于天然地基及复合地基难于满足如此大的上部荷载，故采用桩基础方案（见图3）。主要土层为填土、黄土、古土壤、细砂、粉质黏土。桩基检测项目有成孔质量、桩身完整性、侧摩阻力、单桩竖向极限承载力等检测项目（见图4）。

图3 桩位布置图

图4 滑动测微计现场测试图

2.2 试桩情况

该试桩工程设计钻孔灌注桩13 根，桩径为1000 mm，其中试桩SZ1为3根，SZ2为1根，锚桩9根，试桩桩桩长66.2 m。SZ1、SZ2桩身混凝土强度为水下C50，锚桩桩身混凝土强度为水下C30。试桩单桩竖向承载力特征值11000 k N，试桩极限承载力28000 k N，锚桩抗拔承载力特征值7800 k N。SZ1采用桩端、桩侧复式后注浆，桩侧注浆位置为桩顶标高以下15.0 m、30.0 m、45.0 m。SZ2采用桩端后注浆，锚桩不注浆，定量压浆4000 kg，桩位布置见图3。本次工程每根试桩埋设2根测微管，分段对接，按1 m 间距设置金属测标，管顶高出灌注桩0.3～0.5 mm，安装过程中确保测管平直，满足滑动测试要求。施工过程中采用泥浆护壁、旋挖机械成孔工艺，成孔测试结果显示试桩孔径、垂直度和孔底沉渣厚度满足设计要求，各试桩及锚桩桩身完整性亦符合要求。

3 试验结果分析

3.1 竖向抗压静载试验结果分析

本次静载试验采用慢速维持荷载法进行，各试桩均未达到极限破坏，Q-S曲线均为缓变形，s-lgt曲线没有出现向下弯曲，各桩型的Q-s曲线见图5。试验简要数据见表1。

图5 各桩型静截试验Q-S 曲线

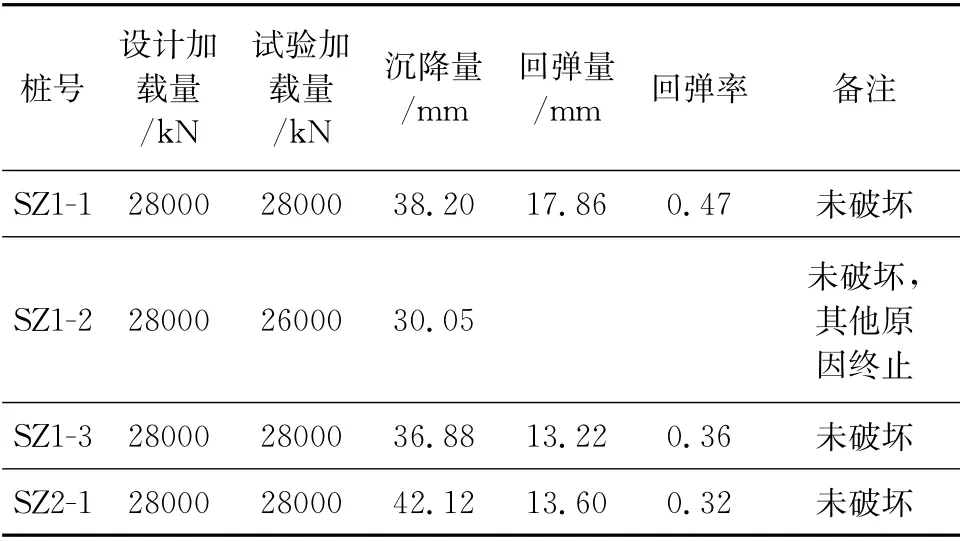
表1 单桩竖向抗压静荷载试验数据

SZ1-2试桩静载荷加载至26000 k N 时，M3锚桩上拔量急剧偏大，无法提供足够的反力，试验终止。经调查，由于天气原因，M3桩成孔完成三天后才进行混凝土灌注成桩作业，造成桩周泥皮过厚，锚桩抗拔力的下降或许与此情况有关。

SZ2-1试桩在28000 k N 在荷载下未发生破坏，总沉降量比SZ1型桩略有增大（约4～5 mm），回弹曲线包络面积相对偏大。这一差异表明侧注浆对桩周土耗能结构的增强以及在长期荷载作用下对沉降的限制作用。SZ2桩型的试桩数量仅为1根，同时考虑到与SZ1桩型的3根试桩距离较近，SZ1桩的侧注浆可能对该桩的承载力有一定的影响。

3.2 桩身内力测试结果分析

荷载试验过程中，通过滑动测微计技术得到SZ1、SZ2桩身在各级静荷载作用下的应变量，本文以SZ1-3桩的试验数据为例进行探讨。为准确获取桩侧阻力和端阻力的发挥过程及分布规律，并考虑各种可能的影响因素，需对实测的桩身应变数据进行一系列必要的计算及分析。

3.2.1 应变断面修正

由孔径测试结果可知，试桩桩径随深度而变化，由此导致桩身各测段实测应变值具有一定变异性，因此将其归一化到桩身平均截面是必要的。根据上述公式1，对SZ1-3桩实测应变进行断面修正，得到修正后的应变-深度关系曲线，见图6。

通过分析可以发现：

（1）试桩桩身应变曲线成锯齿状波动，这与加载过程中桩身内力传递引起的应力变化有关，也与实际桩径及混凝土弹性模量变异有关，而桩的上部应变偏小是实际桩径增大引起的。

（2）试桩在约20～55 m 范围内由大变小趋势明显，说明这一深度范围内的土层能够为桩体提供的侧摩阻力较大，是试桩承载力的主要提供者，其下部的土层主要起稳定沉降的作用。

3.2.2 应变曲线拟合

为消除因局部测量误差引起的离散点，经断面修正后的数据尚应进行应变曲线的拟合，采用约束样条拟合法进行平滑处理，根据回归后的桩身数据绘制桩身回归应变-深度关系曲线，见图7。

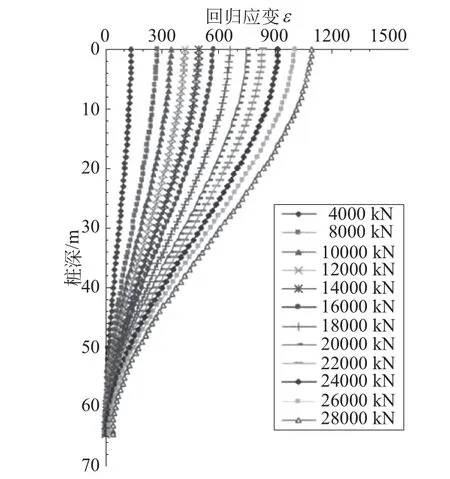
图7 SZ1-3回归应变-深度关系曲线

3.2.3 桩身平均弹性模量

混凝土的应力-应变关系在超过一定的应力水平后呈现非线性特性，其弹性模量将随应变或轴力的增加而降低。为了得到符合实际的桩身轴力，应根据应变量级采用不同的弹性模量，根据上述式（2）、式（3），可得出SZ1-3试桩的平均弹性模量与应变关系曲线（见图8），桩身平均弹性模量方程为：

图8 SZ1-3试桩弹性模量-应变关系曲线

3.2.4 桩身轴力计算与轴力传递曲线

根据桩身应变和混凝土的弹性模量可以计算桩身相应深度处的轴力，见式（4），图9为SZ1-3试桩在桩顶荷载下桩身轴力沿桩身分布曲线。

图9 SZ1-3试桩轴力-深度关系曲线

在桩顶荷载作用下，桩身轴力均随桩深度的增加而递减。桩端应变很小，表明在试验荷载下桩端阻力发挥很小，在终止荷载下承载力发挥以侧阻力为主。

（1）在桩顶荷载作用下，桩身轴力均随桩深度的增加而递减。桩端应变很小，表明在试验荷载下桩端阻力发挥很小，在终止荷载下承载力发挥以侧阻力为主。

（2）在各级荷载下，试桩桩身轴力随桩的深度变化相近，承载力性状表现出一定的稳定性。

3.2.4 桩的侧阻力及端阻力发挥特征

根据已计算的桩身轴力及实测的桩身直径，通过式（5）可以分别计算出试桩在不同荷载下桩身侧阻力及桩端阻力大小，图10绘出了桩顶荷载作用下侧阻力-深度曲线，图11为桩端阻力随桩顶荷载的变化曲线。

分析图10及表2，可知桩侧阻力及端阻力随桩深变化的规律：

（1）在桩顶荷载作用下，侧阻力在桩身某一位置出现峰值，分布形态属于“单峰状”；

（2）峰值的位置变化随桩顶荷载的增加而向下移动；

（3）在28000 k N荷载时，侧阻力的峰值位于距桩顶约38 m处，数值为190.41 kPa。

（4）试桩侧摩阻力发挥段主要为20～55 m，占桩体长度的53%，主要位于桩体以下30%桩长至82%桩长位置；侧摩阻力峰值出现在35～45 m 位置的9-11层，位于桩体以下53%～68%桩长位置，即桩体中部偏下位置；

图10 SZ1-3试桩侧阻力-深度曲线

图11 SZ1-3试桩端阻力-荷载关系曲线

（5）端阻力曲线在20000 k N 时尚无变化，其后出现小幅度的增长，24000 k N 时出现跃升拐点，28000 k N时端阻力达到1384 kPa。

对复式后注浆的SZ1桩型进行竖向抗压静载试验，采用滑动测微计技术进行桩身应变测试，经综合分析，单桩竖向极限承载力作用下，桩的侧阻力及端阻力如表2，折减后SZ1-3 试桩极限承载力取21788 k N。

表2 侧摩阻力及端阻力建议值

4 结语

在西北黄土地区，后注浆灌注桩施工工艺能大大提高桩基的承载力。滑动测微计法是一种行之有效的内力试验技术，利用滑动测微计进行桩身内力测试，有利于加深对桩基承载力性状及桩土作用机理的理解，为今后黄土地区超高层建设提供施工经验及技术指导。更重要的是通过对桩基设计、施工工艺的优化，可以在保证工程质量的前提下，降低工程造价，具有较明显的经济效益。