拉力分散型土层锚索工作机理与性状

赵晓峰

（中国有色金属工业西安勘察设计研究院有限公司，陕西西安 710054）

0 引言

土层锚索在边坡、基坑工程中得到了广泛地应用。土层锚索锚固体长度存在一个临界值，即当锚固段长度超过该值后，长度的增加对锚索极限承载力提高不起作用。也就是说，在实际工程中不能采用单纯增加锚固段长度的方法来提高锚索极限抗拔承载力，这样就限制了预应力土层锚索在深基坑支护中应用。特别对于深度大于20 m 的超深基坑，由于普通土层锚索提供的抗拔承载力有限、支点刚度有限，不得不选择内支撑结构或沉井等其他造价更高、施工效率较低的施工方法。当然也可采用改善锚固段岩土体的工程性能、压力灌浆、扩大锚固段直径等方法来提高锚索的抗拔承载力，但提高的幅度也是很有限的。然而，采用拉力分散型型锚索，设计人员可根据结构体系所需要的拉力值灵活设计锚固体的长度。本文采用简化理论计算及锚索原位拉拔试验实测抗拔承载力的方法，阐述了土层锚索合理的锚固长度，并对拉力分散型土层锚索的工作机理与性状进行了分析。

1 土层锚索的合理锚固长度

1.1 简化理论计算

（1）张 洁等[1]，在假定锚杆与土层力的传递为理想弹塑性荷载传递模型，推导了锚杆临界锚固长度的解析解。表达式为：

式中：E为锚固体综合弹性模量；A为锚固体综合面积；λ为锚杆侧摩阻刚度系数，实际工程中可通过锚杆拉拨试验P-S关系曲线反演得到，它综合反映了多种因素对摩阻力的影响。

（2）龙 照等[2]，假定锚固体与土体之间剪应力呈倒三角形分布，并引入与抗拔桩类似的剪切位移模型，根据锚杆锚固体与周围土体之间的位移协调原理，提出了一种锚杆临界锚固长度的简化计算方法。表达式为：

式中：r0为锚固体半径；Eb为锚固体弹性模量；Es为土的压缩模量；νs为土的泊松比；rm为锚杆的影响半径，已有研究表明[3]，当rm＞20r0后，土体的剪应变已经很小，可以略去不计。

1.2 原位拉拔试验方法

为了解预应力锚索抗拔承载力与锚固长度之间的关系，在西安市西郊某深基坑支护工程中进行了两组共10处，锚索拉拔承载力的基本试验。该工程场地地貌单元为皂河二级阶地，工程基坑开挖深度21 m，自然地下水位埋深约地表下13 m，基坑工程进行了人工降水作业。第一组锚索位于基坑深度6 m处，位于自然地下水位以上的Q4可塑状态的黄土状土层中，共设置5个试验锚索。试验锚索的自由段均为5 m，锚固段长度分别为5、7、9、11、13 m。锚索成孔直径150 mm，配4 根φ15.2-1860钢绞线，锚孔灌注M25水泥浆，自由段采用每根套塑料波纹管隔离法。第二组锚索位于基坑深度12 m 处，位于天然水位以下，主要为Q3冲积成因的可塑状态的粉质黏土层中，其他设计参数与第一组相同。各层土的物理力学指标值列于表1，锚索基本试验数据见表2—表3，第一组及第二组锚索极限抗拔承载力-锚固段长度曲线图见图1—图2。

表1 各层土的物理力学指标

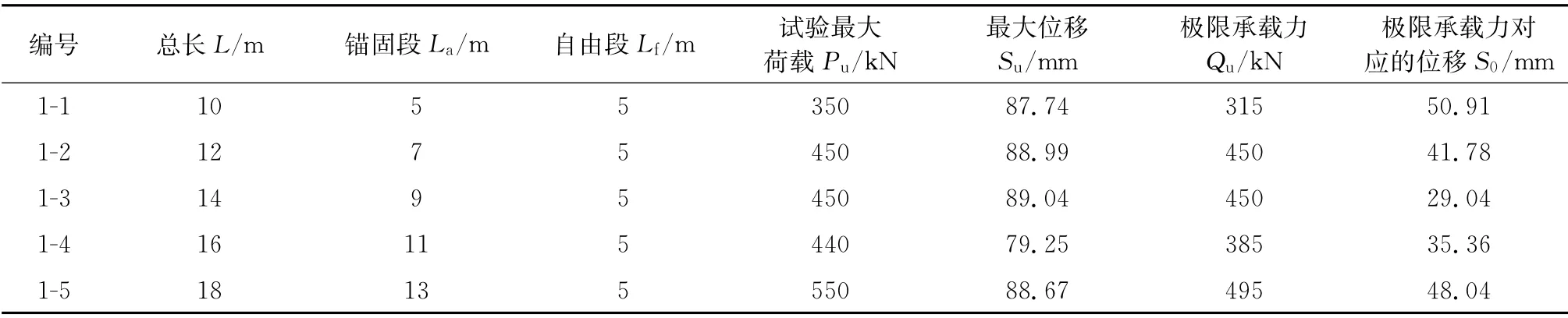
表2 第一组锚索基本试验结果

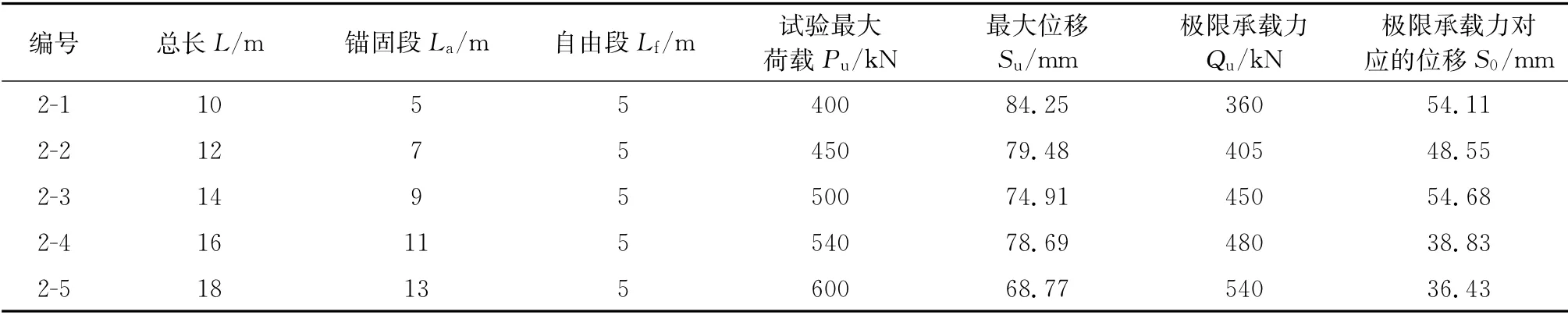
表3 第二组锚索基本试验结果

如图1所示，设锚固段长度为变量x，极限抗拔承载力为f（x），则第一组锚固段长度（x）与极限抗拔承载力f（x）关系回归关系式为：

图1 第一组锚索极限抗拔承载力-锚固段长度关系曲线

图2 第二组锚索极限抗拔承载力-锚固段长度关系曲线

f″（x）＜0，曲线是凸的，令f′（x）=0，则求得x=12.60。即f（x）在x=12.60处取得极大值。因此根据拟合结果对于第一组数据，在锚固段长度为12.60 m 时，极限抗拔承载力f（x）取得极大值。f（12.6）=494.5。

同理，如图2，第二组锚固段长度（x）与极限抗拔承载力f（x）关系回归关系式为：

f″（x）＜0，曲线是凸的，令f′（x）=0，则求得x=13.26。即f（x）在x=13.26处取得极大值。因此根据拟合结果对于第一组数据，在锚固段长度为13.26 m 时，极限抗拔承载力f（x）取得极大值。f（13.26）=530.0。

按文献[2]（龙 照等，2010）提出的锚杆临界锚固长度的简化计算方法：Lc=取锚固体半径r0=0.075 m；锚固体弹性模量Eb=2.8×107kPa；第一组土的压缩模量Es1=9000 kPa；第二组土的压缩模量Es1=7000 kPa；土的泊松比νs=0.35；锚杆的影响半径rm=20r0。求得第一组锚杆临界锚固长度Lc1=20.62 m，第二组锚杆临界锚固长度Lc1=23.38 m。两组原位拉拔试验结果得到的最大锚固段长度与公式所求锚杆临界锚固长度的比值分别为0.611及0.567，约为试验值的0.60倍。

2 拉力分散型土层工作机理

在锚固荷载传递机理方面有大量的成果。如文献[2]在试验和现场测试的基础上采用拟合的方法给出锚固段剪应力的分布规律如：τz=τ0exp，（其中，d为锚体直径，τ0为常数，z为沿锚固体方向长度，剪应力表现为指数衰减形式）。文献[3-4]采用数值分析的方法探讨了锚固段应力分布规律。文献[5]利用无限体内部一点受集中力作用的位移解（即Kelvin问题的位移解）导出了拉力分散型锚固段受拉力作用的应力分布规律，同时得出在提供相同锚拉力条件下，拉力分散锚固型最大剪应力是拉力集中锚固型最大剪应的1/N倍，N为分散锚固段的段数（假定拉力分散型锚固段各段长度相等）。这样在提供同样锚拉力条件下，拉力分散锚固型最大剪应力远远小于拉力集中锚固型的最大剪应力，这就大降低了锚索锚固体与土层界面之间发生剪切破坏的可能性，保证了锚索能提供更大的锚固力。拉力分散锚固型与拉力集中型锚索结构及受力见图3，由图3可以看出拉力分散锚固型锚固段最大剪应力约为拉力集中锚固型锚固段最大剪应力的1/3倍（段数N=3），拉力分散锚固型每组钢绞线的轴力与拉力集中锚固型每组钢绞线的轴力大致相当；拉力集中锚固型锚固段尾部总轴力很小甚至为零，也即并未发挥作用，也就是说拉力集中锚固型如果单纯靠增加锚固段长度的方法来提高锚索抗拔承载力是不行的；而拉力分散锚固型锚固段总轴力沿锚索长度分布很合理，能够充分发挥锚索锚固段的作用，当增加锚固段的段数，就可以成倍的增加锚索的锚固力。

当然拉力分散型锚索受力与张拉工艺也有一定的关系。由于组成锚索各组钢绞线自由段长度不同，其弹性变形大小也不相同，所以拉力分散型锚索分组张拉及整体张拉对各组钢绞线受力影响较大，最好采用先分组张拉再进行整体张拉锁定，或采用补偿荷载整体张拉[6]的方法进行张拉，尽量使各组钢绞线协同均匀受力。

图3 拉力分散型锚固与拉力集中型锚索结构及受力简图

3 拉力分散型土层锚索的构造的改进

在实际工程设计中，特别是在土层预应力锚索设计中，往往对拉力分散型锚索的构造进行适当改进。改进方法如下：

（1）锚索各组自由段长度按照拉力分散型锚索要求设置，但对于各组锚固段钢绞线均通配到孔底。这种改进主要考虑岩土工程的多因素、作用机理复杂、隐蔽工程质量风险大等原因，另外每米钢绞线造价与锚固段尾部仍可提供一定的锚固力相比还是值得多余设置。另一方面，如果万一锚固体前端由于受力大等原因锚固体与土体界面解耦失效条件下这部分钢绞线也能起到储备作用。改进后的土层拉力分散型锚索结构见图4。

图4 改进后的拉力分散锚固结构示意图

（2）每组钢绞线自由段与锚固段有效隔离，一般采用与钢绞线相配套，同径比钢绞线直径略大的一点的塑料波纹管进行隔离，自由段与锚固段接头部位应采用环氧胶泥密封并用胶带包裹牢固。作法见图5。

（3）分组标识不同自由段的钢绞线，在锚索张拉锁定时，应采用先分组张拉再整体张拉锁定。理论上，拉力分散型锚索分段数越多、受力越均匀，提供的锚固力越大，锚固段侧阻力发挥越充分。但在实际工程中一般最多分3段，对土层锚索分段长度约为10 m。

图5 自由段锚固段节点作法

4 结语

（1）在提供同样锚拉力条件下，拉力分散锚固型最大剪应力远远小于拉力集中锚固型的最大剪应力，这就大降低了锚索锚固体与土层界面之间发生剪切破坏的可能性，保证了锚索能提供更大的锚固力。

（2）拉力分散型锚索受力与张拉工艺也有一定的关系。建议采用先分组张拉再进行整体张拉锁定，或采用补偿荷载整体张拉的方法进行张拉，尽量使各组钢绞线协同均匀受力。

（3）实际工程设计中，土层锚索各组自由段长度按照拉力分散型锚索要求设置，但对于各组锚固段钢绞线均通配到孔底。

（4）理论上，拉力分散型锚索分段数越多、受力越均匀，提供的锚固力越大，锚固段侧阻力发挥越充分。但在实际工程中一般最多分3段，对土层锚索分段长度约为10 m。