大型百货商场会员画像描绘的数学模型

唐纪芳

（四川职业技术学院，四川 遂宁 629000）

一、问题重述

在实体零售行业中，会员持续不断的为零售运营商带来稳定的销售额与利润来体现会员自身的价值，也为运营商提供制定策略的数据支持。对现有会员的画像进行完善，加强对现有会员的管理，定期的推送适合的产品和服务，与会员建立稳定的关系，以使实体零售行业的发展更好。

附件(文献[1]）中的数据给出了某大型百货商场会员的相关信息：附件1 是会员信息数据；附件2 是近几年的销售流水表；附件3 是会员消费明细表；附件4 是商品信息表，一般来说，商品价格越高，盈利越高；附件5 是数据字典。请建立数学模型解决以下问题：

问题一：对每一位会员的消费情况进行分析，建立能描绘每一位会员的购买力的数学模型，以方便能够对每位会员给商场带来的价值进行评估。

问题二：从非活跃会员转化为活跃会员的可能性称为激活率，建立数学模型后计算出会员的生命周期中的非活跃会员的激活率并从实际的销售数据出发，确定非活跃会员的激活率和商场促销活动之间的关系模型。

问题三：销售之后再销售被称为连带销售，而连带销售是购物中心经营的重心，假如商家将策划某次促销活动，怎样根据会员的爱好和商品所带来的连带率来策划这次促销活动。

二、问题分析

问题一：本题要求对比会员与非会员的销售差异。首先进行数据处理，对附件2-销售流水表的内容进行时间分析发现起止时间是2016 年1月9 日到2017 年9 月23 日，附件3- 会员消费明细表的时间分析发现起止时间是2015 年1 月1 日到2018 年1 月3 日，并对附件3 中不含附件1 的其他会员进行筛选，后取附件2 与附件3 的相同时间段（2016 年1 月9 日-2017 年9 月23日）来比较会员在此段时间所购买商品的总金额与非会员购买商品的总金额，并计算出会员与非会员分别所占的比例。

问题二：本题首先对生命周期进行定义，其次对会员的状态进行划分，整理附件1、附件2、附件3 后统计出2015 年上半年到2018 年上半年的生命周期和活跃状态，最后对附件3 数据分析后建立马可夫链模型[2]来解决会员的生命周期与状态划分。对附件1 和附件3 进行整理定义出促销时间，最后选出促销时间，再对附件3 中促销时间前的会员消费状态进行统计，然后对会员的状态进行标记，统计出激活会员与非活跃会员和流失会员的和，最后建立模型计算出激活率。

问题三：定义连带销售，连带率。分析所有类别的商品销售数量，其次分析每个会员购买商品的数量及金额情况，推算出受大众喜爱的商品从而决定促销方案。然后建立连带率的计算模型。

三、模型假设

1)题目附件的大型百货商场的销售数据真实可靠，会员卡号反应出的人数准确。

2)假设大量数据中舍去或者补充少量部分数据不影响最后结果。

3)题中并未给出具体的会员生命周期状态规则，结合现实和附件数据给出较为合理的定义。

4)假设每个会员卡号仅限本人使用，且商场不会发生剧烈的变化影响销售。

四、符号说明

mi：总金额

d:某个时段

Si:第i 半年时间段所在的列

Ki：第i 个会员喜欢的商品连带率

Mi：第i 个会员购买的商品类别里数量最多的商品数量

Zi：第i 个会员购买的所有商品类别的数量

五、模型建立与求解

问题一

购买力（purchasing power）是指在一定时期内用于购买商品的货币总额，这个定义中需要考察两个因素，一个是两次消费间隔的时间，一个是相同时间的消费金额。因此我们规定在一定时间内，消费金额越高的会员，则购买力越高，相同的消费金额如果消费间隔时间越短，则该会员购买力越高。我们根据附件3 中会员消费情况，首先考虑会员的性别，年龄因素对商品购买数量，金额进行统计，结果如表1。再考虑不同年龄阶段和性别对不同类别商品的购买数量和金额，来反应出会员对某类商品的购买力，因此我们建立了一个随着时间的增加，消费金额的变化而产生变化的购买力的数学模型。根据这个模型得出各会员的购买力情况，购买力越高的会员价值越高。

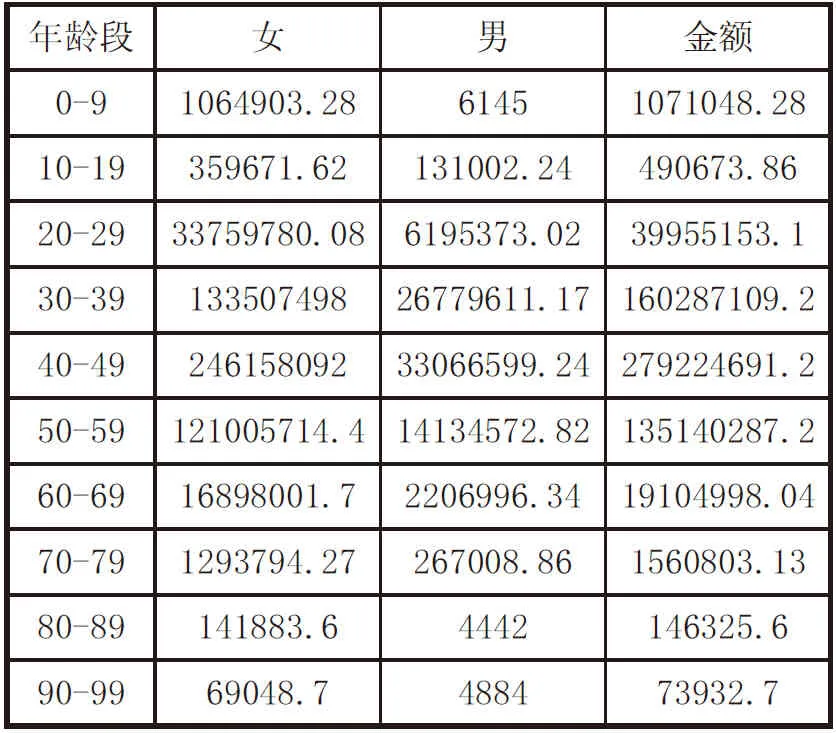
表1 消费金额情况表

根据消费金额情况可以建立每一个会员平均消费金额的模型：

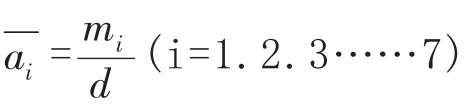
利用Excel 软件挑选出一部分会员的购买情况算出各个会员的平均消费金额来反映购买力见表2.

表2 会员购买力

从表2 可以看出每个会员的购买力不同，数据越大时说明该会员在此时间段内购买力越大，数据为0 时该会员在此时间内未购买任何商品。

问题二

会员包含各种类型，反应了不同群体的特征和想法。在会员的生命周期中，我们应定义更全面的指标。

流失会员：有一段时间没有购买产品，那么我们就视为流失会员，根据会员购买情况，我们可以把这段时间按360 天划分。即该会员360 天内没有购买任何产品，就视为流失会员。在上一次购买或者开卡时到流失会员的时间段就是该会员的生命周期。

在生命周期里我们对会员状态有以下定义[3]：

非活跃会员：有一段时间没有购买产品，为了和流失会员区分开来，需要选择无交集的时间范围。比如流失会员是360 天以上没购买产品，那么非活跃会员则是180 天～360 天没购买。

活跃会员：一段时间内购买过产品，我们以180 天内购买产品来划分。

激活会员：有一段时间没购买产品，之后突然回来再次购买，则称为激活会员。激活会员是活跃会员，且是由流失会员或非活跃会员转变而来，即超过180 天没有购买商品然后又购买商品的会员。

会员购买商品是一个随机的无后效性的动态过程，每一个时间段里会员所处的状态是随机的，这一次购买，不能反应出下一次是否购买，这次购买下次有一定的概率转移成不购买。同样，这次不购买，下次有一定的概率转移成购买。也即是说下一个时期的状态只取决于本时期的状态和转移概率[4]。

会员在生命周期内具有活跃、非活跃及流失三种不同的状态，设对特定年龄段的人，现阶段活跃下阶段保持活跃状态的概率为0.5,而现阶段非活跃、下阶段转为活跃状态的概率为0.5，现阶段非活跃，下阶段转为流失状态的概率为0.3，可以建立下面的模型(马可夫链模型)：

初始阶段的活跃值与初始状态相同，

当Si+1=1，(i=0,1,2,…,6）时,该会员在此阶段活跃；当，(i=0,1,2,…,6）时,该会员在此阶段非活跃；

当Si+1=0，(i=0,1,2,…,6）时,该会员在此阶段为流失。

表3 不同状态下的会员人数

激活率：即从非活跃会员或者流失会员转化为活跃会员的可能性[5]。

促销时间：对附件1 和附件3 的数据做合并处理，算出日平均销量为307，和日平均购买人数为290，选出当天销售数量和购买人数分别超过2.6 倍和2 倍为促销时间（见表4）。

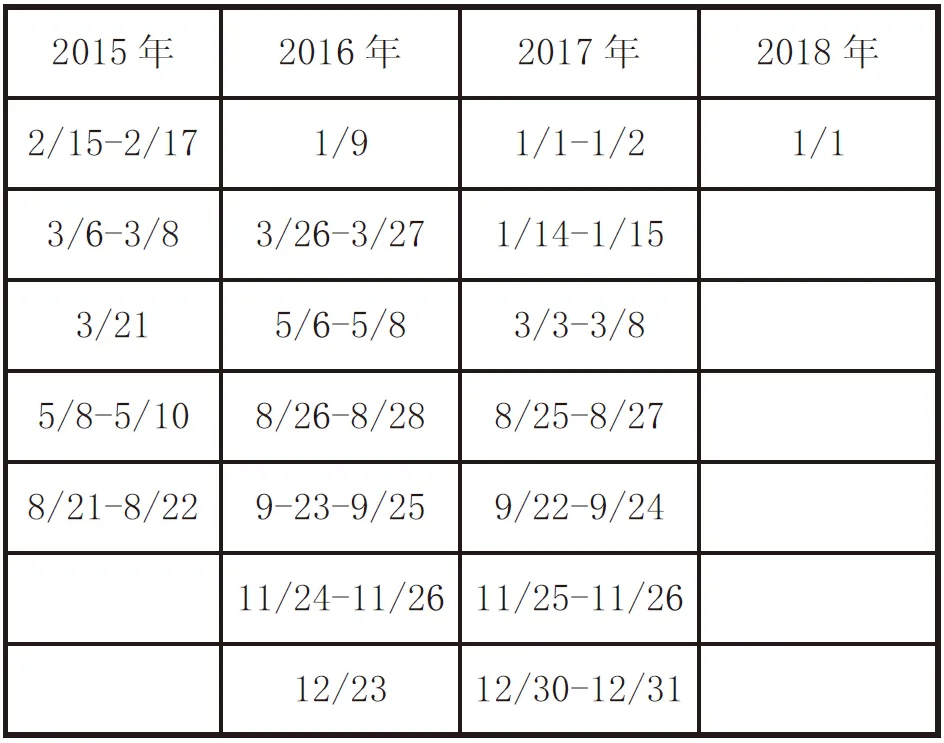
表4 促销时间

再对附件3 中促销时间前的会员消费状态进行统计，若该会员是非活跃状态和流失状态，则标记为0，然后再对促销时间段这些标记为0 的会员进行对比，若该会员变为活跃状态则该会员被激活，

也即是Si-Si+1〈0,(i=0,1,2,…，6）

再根据激活会员的总人数与所有非活跃及流失状态的会员总人数作百分比，该值就是激活率（见表5）。

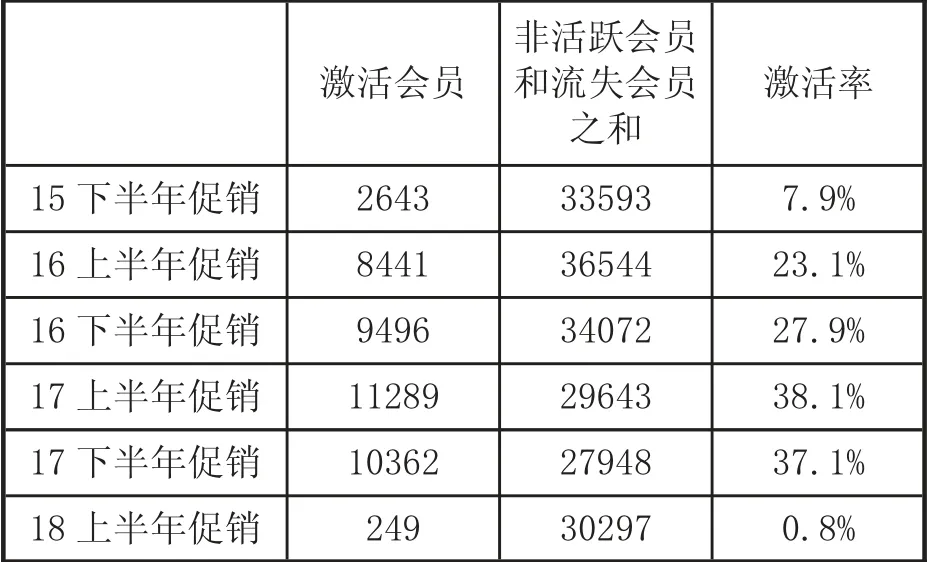
表5 会员激活情况

2015 年下半年只有一次促销活动，所以激活率较低为7.9%。2017 上半年有3 次促销活动，但中途有的促销活动时间较长，所以激活率最高为38.1%。而2018 年只有一次且仅有一天活动时间，所以激活率最低为0.8%。

将每个阶段会员的激活率与其对应阶段的促销时间天数拟合得到下面的函数及图形（见图1），我们通过对数据的分析和拟合可以得出结论：商场促销活动次数越多，时间越长，会员的激活率就越高。

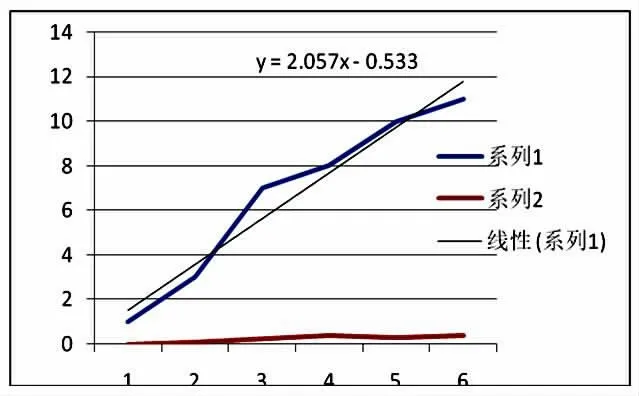
图1 会员激活函数

问题三

首先我们对连带消费下一个定义, 顾客单次购买商品的数量超过1 件,那么超过的商品就是连带消费的商品。

然后分析了所有类别的商品销售数量, 销售数量越多, 说明这类商品越受大多数顾客的喜欢。其次分析每个会员购买商品的数量及金额情况,同样购买的数量越多,消费的金额越高,反应了此类商品越受该会员的喜欢。我们结合两者来讨论促销方案。

假设会员主要购买的是其喜欢的商品, 那么他购买的其他商品就是连带商品,购买的连带商品越多,则此类商品的连带率越高。

我们在搞促销活动时就主要以连带率高的商品来做促销活动,从而带动其他商品的消费。连带率计算模型:

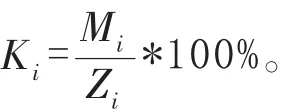
表6 商品连带率

选择连带率超过60%的商品来做促销活动，其中有类别编码为40101，40501，90901，60101，90702 等等，其余见附件7。

六、模型的评价与改进

模型的优点：建模能与实际紧密联系，结合实际情况对问题求解，使模型更贴切实际，推广性较强[6]。模型对数据的分析不仅使问题得到了解决，而且还能迅速掌握实验数据的特点，为建立更合适的模型提供了基础。模型操作简易，适合大众应用。模型试用与各种数据分布，指标多少没有限制，较为灵活，方便。模型可以通过统计方法来对干扰因素加以控制，发现自变量与因变量之间的关系。模型复杂因素较多，不能对其进行全面的考虑，造成与实际有一定的不相符之处，但偏差不是很大。