圆外切四边形一个性质的探索与发现

李 飞

(扬州大学附属中学东部分校 225003)

1 问题呈现

《数学通报》2013年第6期数学问题解答栏目编号为2126的问题是这样的：

如图1，已知四边形ABCD是⊙I的外切的四边形，则下列恒等式成立：

供题者在《数学通报》2013年第7期给出了该题的三角解法.

2 尝试新证

此命题结论结构优美，遂尝试纯几何证法，最终用面积法将其证出，并有其它发现.

从简单问题入手，首先思考：如果是三角形有没有类似的结论？经过探索，发现：

结论1如图2-1，如果△ABC是⊙I的外切三角形，则有

图2-2

证明(面积法)设内切圆与△ABC的切点分别为D、E、F，如图2-2，

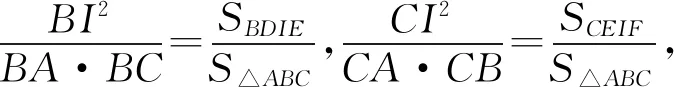
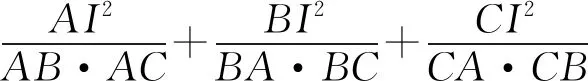
接下来，尝试用面积法证明本文开头提到的命题，即证明：

分母不同，四个分式如何相加？

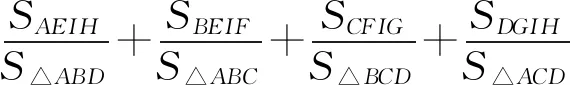
经过推证，以上猜测正确.现将完整证明过程整理如下：

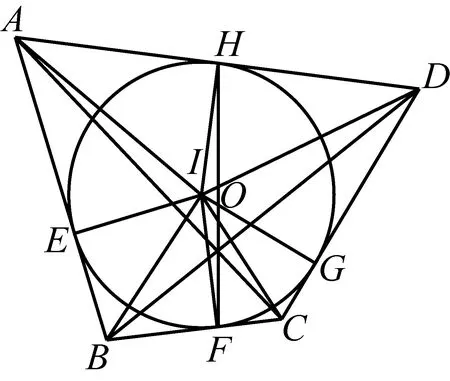
图3

为了推导的方便，将用到的关系先列如下：

如图3，连接AC、BD相交于O，连接FH；

①设SABCD=S，S△AEI=S△AHI=S1，

S△BEI=S△BFI=S2，S△CFI=S△CGI=S3，

S△DGI=S△DHI=S4，

则有2S1+2S2+2S3+2S4=S；

②IH=IF；

③∠DHF=∠CFH，则∠AHO+∠CFO=∠AHO

+∠DHO=180°，

所以sin∠AHO=sin∠CFO.

证明第一步，推导

过程如下：

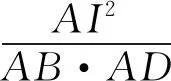
由牛顿定理3可知，对角线AC、BD、线段FH交于点O，

又sin∠AHO=sin∠CFO,sin∠AOH=sin∠COF，

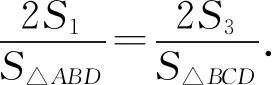
至此可以得到圆外切四边形的一个性质：

由等比性质可得

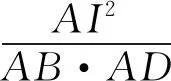
所以

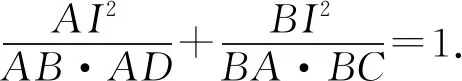
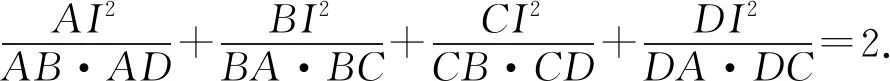
3 探究发现

在探索问题过程中，发现了一个与牛顿定理2相关的结论.

结论2四边形ABCD是⊙I的外切的四边形，对角线AC、BD相交于点O，M、N分别为AC、BD的中点，则有

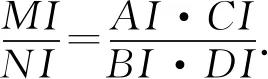
图4

证明前面已经证得

若S1=S3，S2=S4，

则S△ABD=S△BCD，S△ABC=S△ACD，M、N、O重合.

若S1=S3，S2=S4中至少有一个不满足，

不妨设S1≠S3，

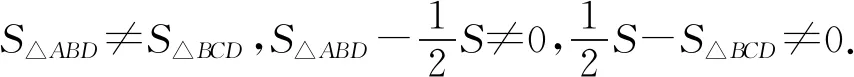
于是，由等比性质可得

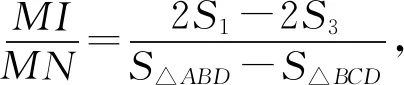
如图4，连接MN、MB、MD，由牛顿定理2可知，MN经过点I.

于是

又

由等比性质可得

同理可得

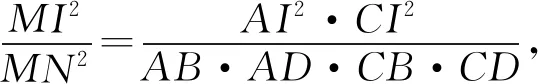
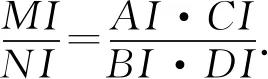
由本结论很容易得到

结论3如图5，四边形ABCD是⊙I的外切的四边形，M、N分别AC、BD的中点，延长AN、BC相交于点P，延长AI、EC相交于点Q，则PQ//AB.

图5

证明由前面证明可知

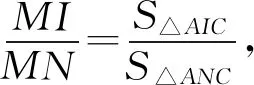
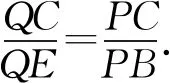
所以PQ//AB.(证毕)