基于轮轨关系的钢轨打磨代表廓形计算方法研究

丁军君， 吴朋朋， 王军平， 李 芾

(1. 西南交通大学 机械工程学院, 四川 成都 610031； 2. 中铁物轨道科技服务集团有限公司, 北京 100036)

钢轨打磨是当前铁路的重要维护保养手段，可有效地预防和抑制钢轨波磨、侧磨和滚动接触疲劳等病害的产生[1]，同时能有效降低轮轨噪声[2]，在提高钢轨使用寿命、改善铁路运行安全性和经济性等方面具有重要作用[3]。当前钢轨打磨模式已由传统的修理性打磨转变为预防性打磨，即在打磨过程中通过控制钢轨的型面来达到钢轨保护的目的[4]。预防性钢轨打磨作业的主要流程为：对待打磨区段的钢轨廓形进行测量和采集，并从中选择一个钢轨廓形作为该组测量数据的代表廓形；将钢轨代表廓形与设计廓形(目标廓形)进行对比，根据对比结果对打磨电机的磨石角度进行排列，最终利用钢轨打磨列车将现有的钢轨廓形打磨成设计廓形(目标廓形)，具体流程见图1。

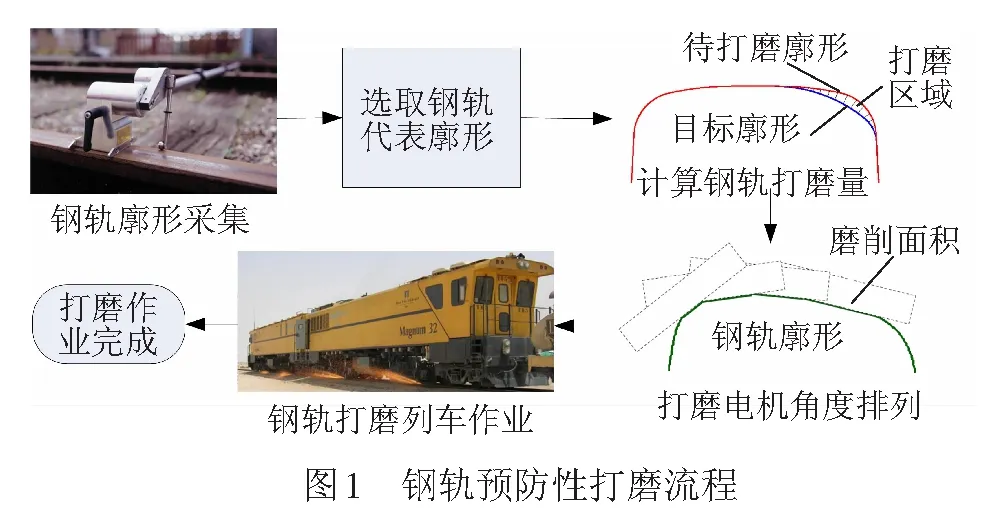
目前国内外对钢轨打磨技术的研究集中在打磨廓形设计、打磨工艺和打磨列车动力学等方面[5-8]，但尚未开展钢轨代表廓形选取方法的研究。在打磨作业的实际操作过程中，钢轨代表廓形由工作人员根据经验选取，效率较低，结果不稳定，同时对操作人员的素质要求较高。本文基于轮轨接触几何关系及分布特点，研究钢轨代表廓形的计算方法，为现场操作人员稳定快速地获得较为准确的钢轨代表廓形提供理论依据。

1 钢轨廓形的平滑处理

目前，钢轨廓形的采集主要依靠机械接触式或者激光非接触式的钢轨廓形测量仪器，所得廓型曲线的采样点间距0.1～0.3 mm，通常存在较小的波浪形抖动，幅值一般小于0.01 mm，仅在极个别的位置干扰幅值可能超过0.05 mm，并有一定概率产生折线或交叉线式的偶发脉冲干扰，受其影响的区域一般为3～5个连续测量点。由于数据中的波浪形抖动或偶发脉冲干扰会对后续的钢轨分析计算准确性产生较大的影响，需对实测廓形数据进行数据滤波和曲线平滑处理。如果抖动或干扰幅值过大，平滑滤波方法不能有效处理，但测量人员在现场可发现，通过重新测量、调整测量点等方式解决。

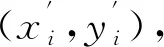
( 1 )

式中：m为半窗宽点数量；hv为第v个点的平滑系数，v为以所取各点相对于取点中心i的位置。

令卷积平滑系数H=[hv]，H可通过最小二乘多项式拟合进行求解。H一般为一个(2m+1)×(2m+1)的中心对称方阵。如果平滑对象是一维数据，H可仅取其最中间一行。

对(2m+1)个以v=0为中心的连续数据点xi，用N阶多项式来拟合，即

( 2 )

式中：p为拟合函数；at为拟合多项式各项系数。

最小二乘拟合残差εN为

( 3 )

对残差式( 3 )求偏导，并令bvt=vt，由此构造矩阵B=[bvt]，于是可得卷积平滑系数

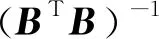
( 4 )

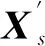
( 5 )

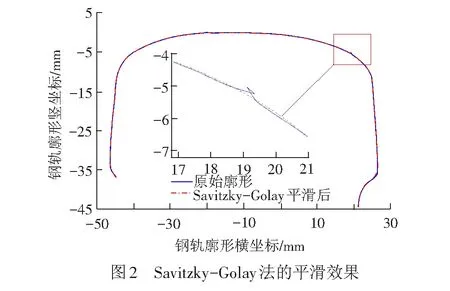
利用Savitzky-Golay法对某钢轨廓形的平滑效果见图2。

为评价各种方法的平滑效果，引入光滑度S和拟合度F两个指标来评价平滑算法的优劣，光滑度S用于衡量曲线的光滑程度，而拟合度F则用于衡量平滑后曲线与原曲线的偏离程度，S越小说明获得的曲线越平滑，F越小表明处理后曲线与原曲线的偏离程度越小。光滑度S和拟合度F分别为

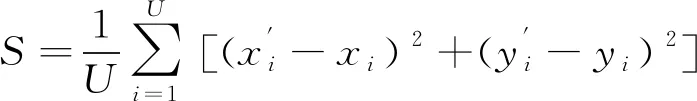
( 6 )

( 7 )

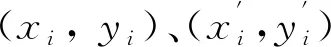
对于图2所示的钢轨原始廓形，利用各种平滑算法进行平滑后，不同窗宽下的平均光滑度和平均拟合度的比较结果见表1。可以看出：与滑动平均法、高斯平滑法和中值滤波法相比，Savitzky-Golay平滑法既能很好地保持曲线形状，又能达到较好的平滑效果，因此钢轨分析中，均采用Savitzky-Golay平滑法对钢轨廓形测量数据进行平滑处理。

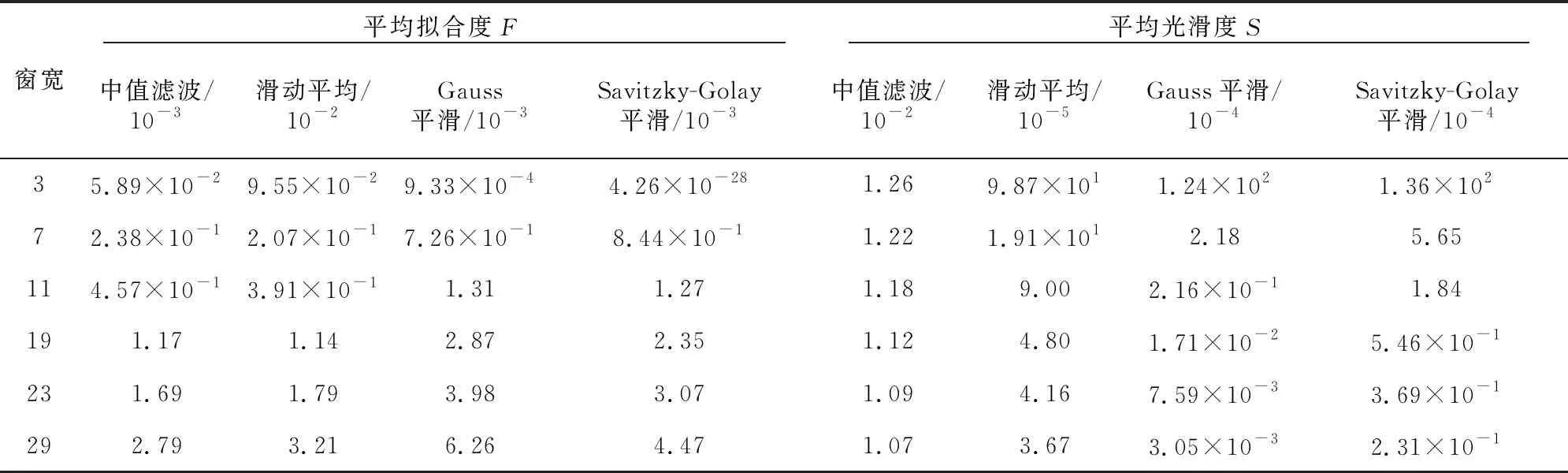
表1 各种平滑算法中窗宽对平均光滑度和拟合度的影响

2 钢轨代表廓形的算法及评价方法

2.1 钢轨代表廓形的算法

(1) 算术平均法

算术平均法是指依次计算钢轨廓形在各个位置上的平均值，然后由得到的平均值坐标构成新的廓形曲线。采用算术平均法得到的代表廓形在i位置上的坐标(xi,yi)为

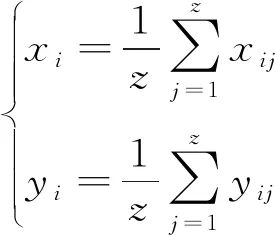
( 8 )

式中：z为测量廓形的总数；(xij,yij)为第j条廓形曲线在i位置上的坐标，i=1,2,…,n，n为每廓形坐标点数量；(xi,yi)为代表廓形在i位置上的坐标。

(2) 加权平均法

在计算平均值时，对每个变量设置适当的权重，然后计算其加权平均值，可以有效抑制少数值、极端值的影响，即加权平均法。加权平均法的计算式为

( 9 )

(3) 最小二乘距离法

根据最小二乘原理，第j条廓形与其他廓形的距离平方和为

(10)

式中：k、j为廓形曲线编号；Dj为第j条廓形与其他廓形的最小二乘距离之和。

最小二乘距离法就是从已知廓形中找到使最小二乘距离Dj最小的廓形曲线，这种求距离平方和的方式可以避免正负距离相抵，且便于数学处理。

(4) 散点拟合法

首先将各个廓形曲线上的数据点打散，组成一个平面点集，然后通过数据点的重排、平滑滤波和曲线拟合等操作获得一条拟合曲线。

如果采用最小二乘法进行曲线拟合，即令拟合误差M为

(11)

通常认为在偏导数均为零时，M可达到最小值，即

(12)

整理可得

(13)

2.2 钢轨代表廓形评价方法

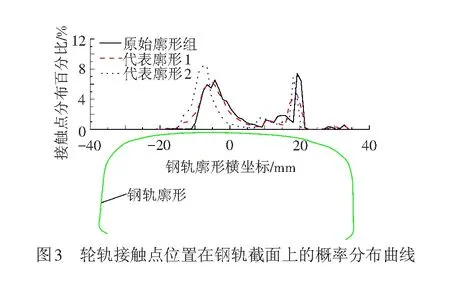
钢轨廓形打磨是通过打磨改变钢轨的廓形，从而改变轮轨接触几何关系。因此，轮轨接触几何关系将作为本文中钢轨代表廓形算法的主要评价依据。将实测的原始钢轨廓形与钢轨代表廓形分别与实测的车轮踏面廓形进行接触几何计算，并对轮轨接触点位置在钢轨不同横向位置的分布和累积概率进行统计，见图3。代表廓形的接触点概率分布曲线与原始廓形越接近，表明钢轨代表廓形算法的计算结果越合理。文中将用Pearson相关系数、Spearman秩相关系数和Cosine相似度衡量接触点概率分布曲线的接近程度。

2.2.1 Pearson相关系数

Pearson相关系数PXY主要用于衡量两个变量之间线性相关性的强弱程度，用两个变量X和Y的协方差与标准差积的商来表示[10]，即

(14)

式中：μX、μY和σX、σY分别为变量X、Y的均值和标准差。Pearson相关系数的绝对值满足条件|PXY|≤1，|PXY|越大，接触点分布曲线的相似性越高。

2.2.2Spearman秩相关系数

Spearman秩相关系数SXY主要用于衡量两个变量之间联系强弱程度，通常用于评价变量间的非线性相似关系，也被认为是变量排列后的Pearson线性相关系数[11]。计算方法：将长度均为N的两变量X和Y按从小到大排序，分别用pi、qi表示xi、yi在排序后列表中的位置，称pi、qi为xi、yi的秩次，将各秩次代入下式进行计算

(15)

值得注意的是，PXY和SXY均不会随着变量的位置和缩放比例而发生变化，意味着即使PXY和SXY都达到极值1，也不能表明两变量完全相同。因此，需要使用Cosine相似度来进一步表述两变量的相似程度。

2.2.3Cosine相似度CXY

Cosine相似度是将两个变量分别映射到向量空间，利用两个变量空间向量夹角的余弦值来衡量差异程度，因此又称余弦距离[12]。两变量X和Y的余弦相似度的计算式

(16)

与前两个指标相似，通常|CXY|≤1，且余弦相似度的值越接近1，表明两空间向量的夹角越小，即两个变量近似程度越高。

3 计算实例及结果分析

3.1 直线区段钢轨廓形分析

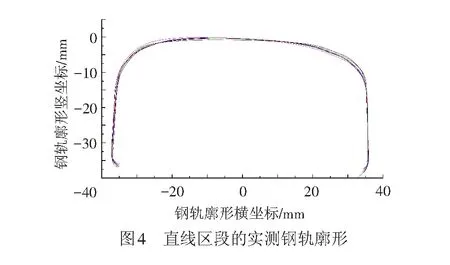
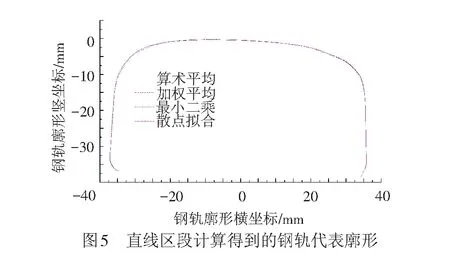
在直线区段，每间隔20 m采集一次钢轨廓形，共采集8个钢轨截面，见图4。按照2.1节中的4种方法算得的代表廓形结果见图5。

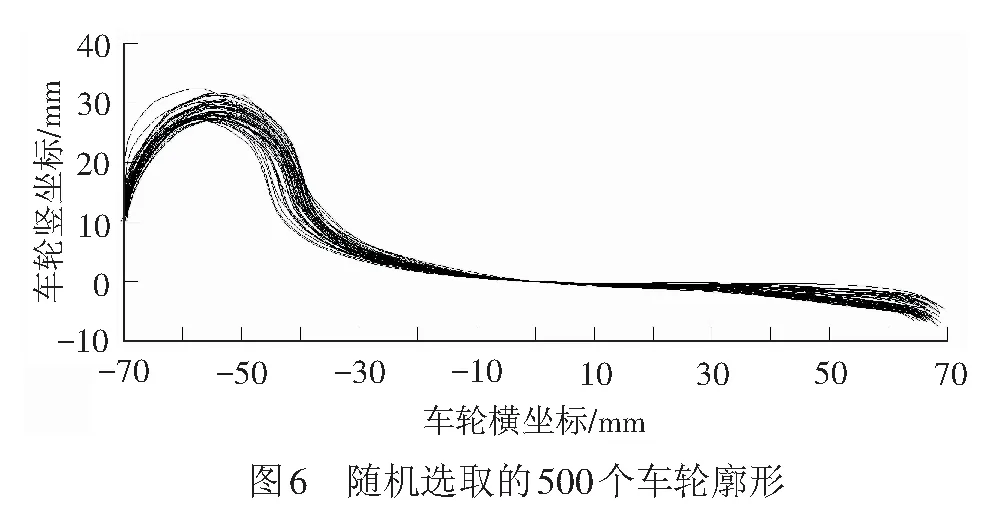
为更准确分析轮轨接触关系，在钢轨采样点附近的机务段、车辆段和货运编组站对在采样钢轨上运行车辆的车轮廓形数据进行随机采集，其中货车车轮320个，客车车轮120个，机车车轮60个。车轮廓形见图6。

由于车轮廓形的测量方法和钢轨廓形一致，因此也采用Savitzky-Golay平滑法对车轮廓形测量数据进行平滑处理。将图5中4种代表廓形分别与图6所示的500个车轮进行匹配并计算轮轨关系，轮轨接触点在钢轨上的分布和累积情况见图7。各种计算方法对应的相关系数的平均结果见表2。

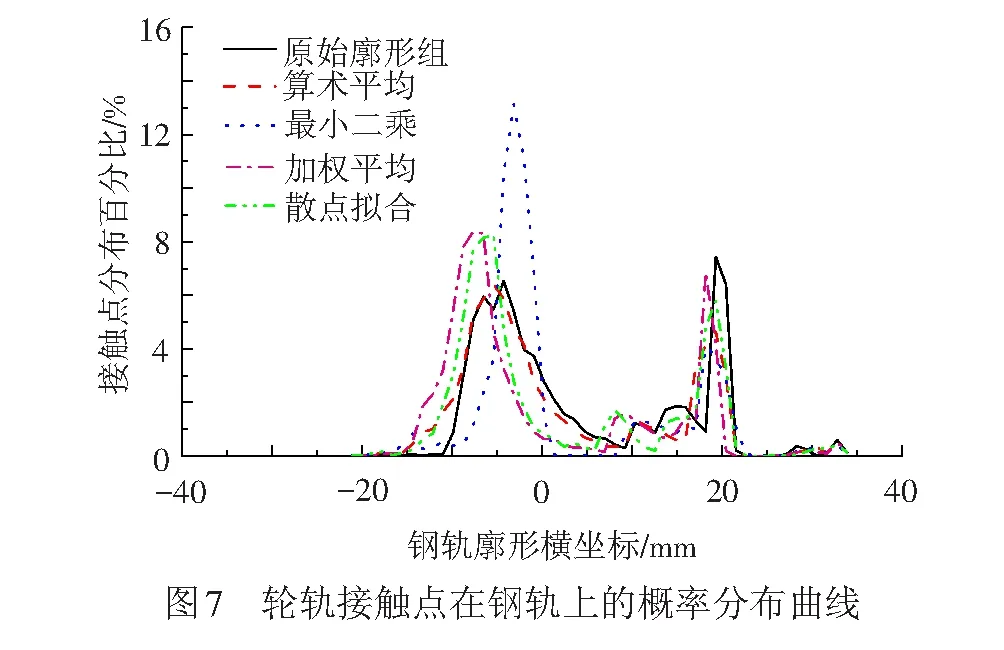
表2 直线区段测量廓形及代表廓形接触点分布相关系数计算结果

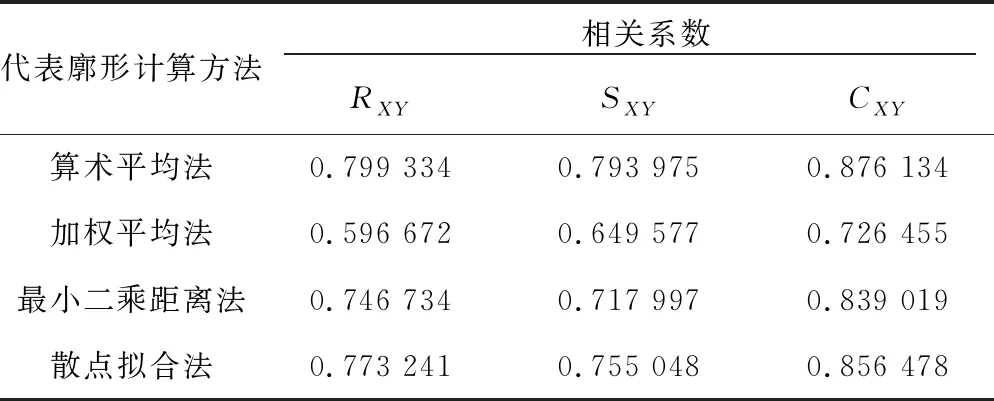
代表廓形计算方法相关系数RXYSXYCXY算术平均法0.799 3340.793 9750.876 134加权平均法0.596 6720.649 5770.726 455最小二乘距离法0.746 7340.717 9970.839 019散点拟合法0.773 2410.755 0480.856 478

从表2中可以看出，对于直线区段内的代表廓形与实测廓形的轮轨接触点分布曲线，算术平均法对应的RXY、SXY、CXY均最大，散点拟合法次之，而加权平均法最小。因此，直线区段钢轨的代表廓形可采用算术平均法或散点拟合法进行计算。

3.2 曲线区段钢轨廓形分析

由于曲线上包含缓和曲线区段和圆曲线区段，而在钢轨打磨时，起缓和曲线的后半段和终缓和曲线的前半段的打磨模式与圆曲线一致，因此本文中曲线区段的钢轨廓形采集点有8个，具体位置见图8。

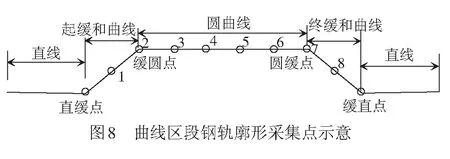
按照图8中的位置在同一条曲线上采集到的8个钢轨截面见图9，各种方法算得的代表廓形结果见图10。

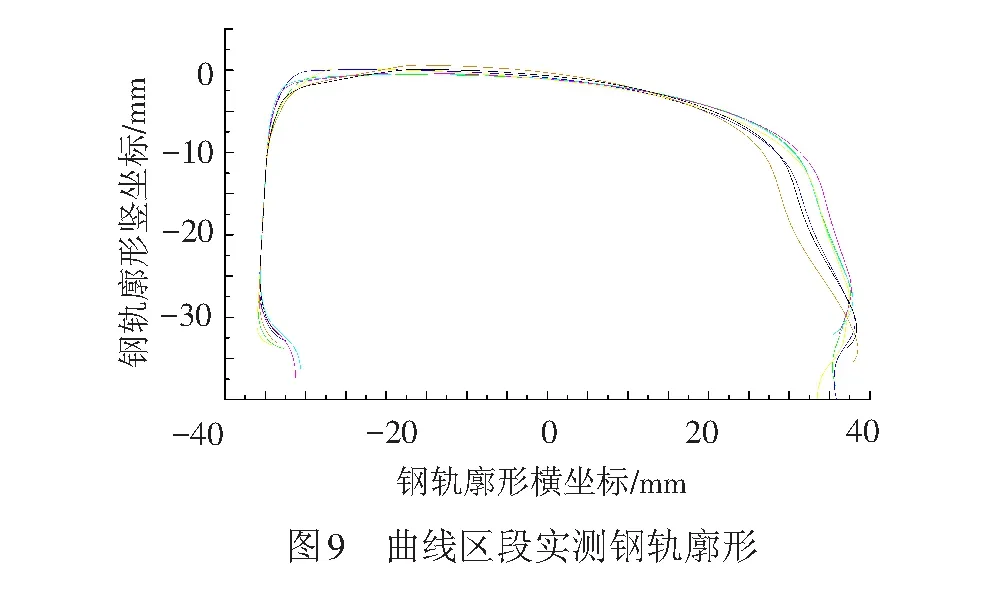
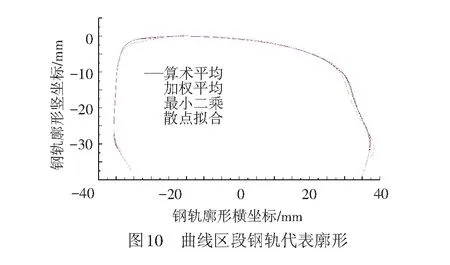
将图10中的曲线钢轨代表廓形与图6的所有车轮分别进行几何匹配并分析轮轨关系，轮轨接触点在钢轨上的分布和累积情况见图11。各种计算方法对应的相关系数的平均结果见表3。

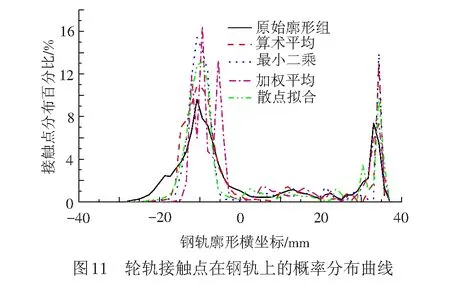
表3 曲线区段测量廓形及代表廓形接触点分布相关系数计算结果

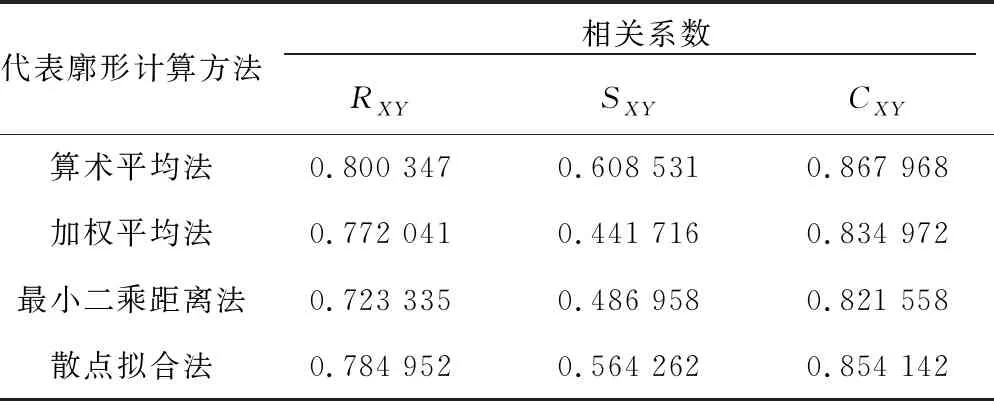
代表廓形计算方法相关系数RXYSXYCXY算术平均法0.800 3470.608 5310.867 968加权平均法0.772 0410.441 7160.834 972最小二乘距离法0.723 3350.486 9580.821 558散点拟合法0.784 9520.564 2620.854 142

由表3可知，对于曲线区段内的代表廓形与实测廓形的轮轨接触点分布曲线，算术平均法对应的各种相关系数均最高，散点拟合法略低于算术平均法，加权平均法最小。因此，曲线区段钢轨的代表廓形可采用算术平均法或散点拟合法进行计算。

4 结论

(1) 对于钢轨廓形的实测数据，利用Savitzky-Golay法进行平滑处理时的光滑度和拟合度较好，不仅能很好地保持曲线形状，而且能达到较好的平滑效果。

(2) 不论在直线区段还是曲线区段上，在各种钢轨代表廓形计算方法中，对轮轨接触点分布曲线与原始钢轨廓形的相关系数来说，算术平均法均最高，散点拟合法略低于算术平均法，而最小二乘距离法及加权平均法的效果较差。因此，建议选用算术平均法或散点拟合法计算钢轨代表廓形。