数形结合思想在小学数学教材中的应用分析——以人教版为例

熊庆

（长江师范学院 文学院，重庆 408000）

一、课题的提出

新课程标准修改后，将“双基”改为了“四基”，即基础知识、基本技能、基本思想方法、基本活动经验，这就说明了人们已经意识到数学思想方法的重要性。这一转变并不是偶然的，而是纵观小学数学学习内容和小学生的认知特点而决定的。常用的数学思想方法之一就有“数形结合”思想。

数与形一直以来都是数学的主题，即使如今的数学有着庞大的分支，仍不可磨灭它的影响力。华罗庚先生的打油诗：“数无形，少直观；形无数，少入微”向我们展现了数与形密不可分的关系。简单的说，数与形就是抽象与形象的表现，数是形的抽象概括，形是数的直观表现，数形结合更加有利于学生对知识的理解，单纯的数使知识缺乏直观性，同样的如果只有形就少了几分严密性，由此可见只有将“数”与“形”结合起来才能发挥出巨大的作用。

二、应用分析

数形结合思想在小学数学教材中有着许多巧妙的应用，如下：

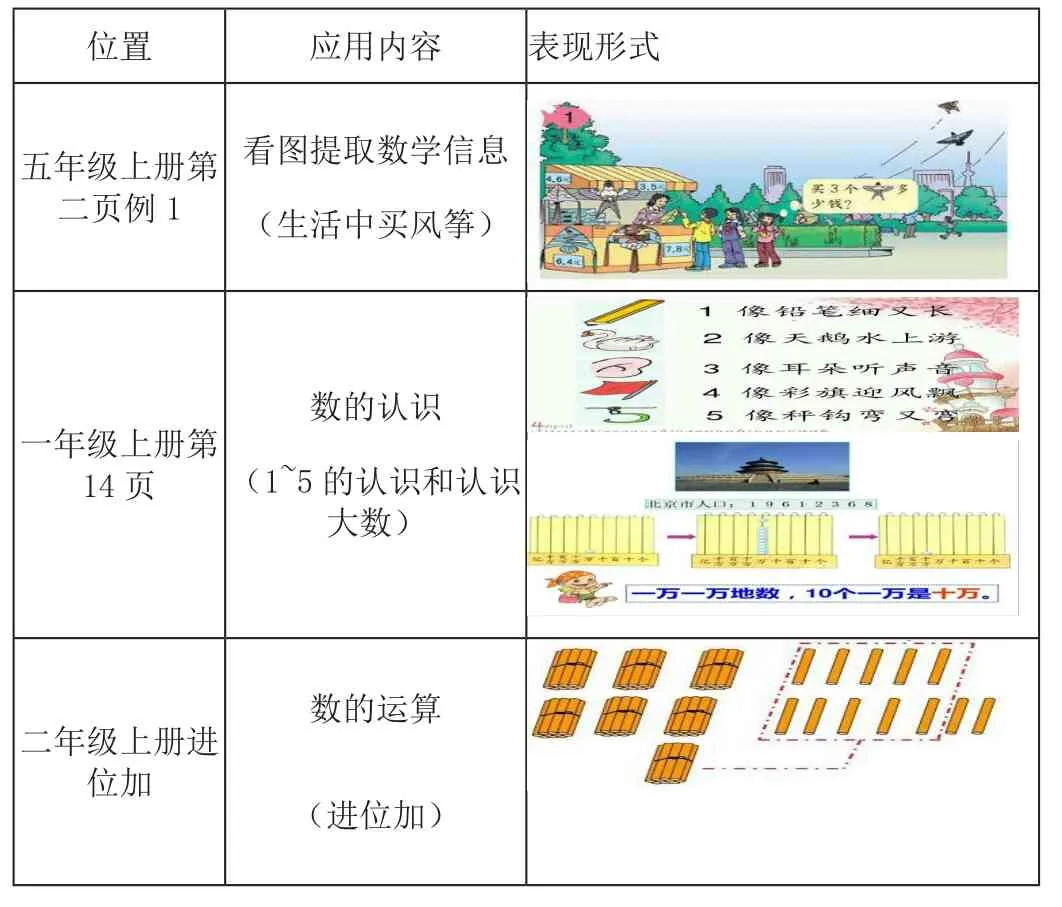
表1 数形结合思想在教材中中的应用统计图

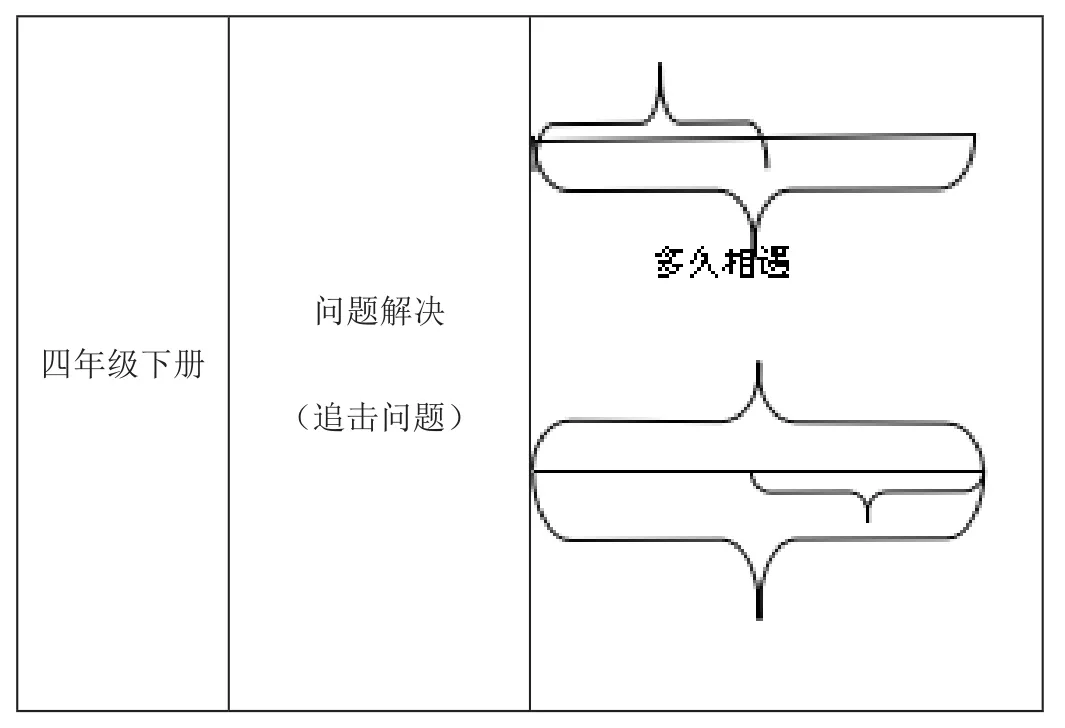
问题解决images/BZ_74_1814_720_2263_1003.png四年级下册（追击问题）images/BZ_74_1814_1019_2270_1281.png

（一）数形结合体现在看图提取数学信息

分析：这个例题中，首先情境很好地展现了“形”，以我们生活中熟悉的风筝作为素材，图中的对话包含了数学信息，在每个风筝上标出了价格，提出数学问题，这就将“数”展现了出来，而不是直接以应用题的方式将条件和问题呈现出来，所以从这道题可以看出来数形结合思想不仅让学生学会从“形”中提取“数”，还加深了学生对数的理解。这类题目的出现，充分体现了素质教育的全面推广，数形结合思想的结合帮助提高学生的学习能力。

（二）数形结合思想体现在关于数的认识

分析：这道题是1~5的认识，在小学阶段，数学的学习是从认识数开始的。低段的小学生大脑没有发育完全，抽象思维对他们来说比较困难，在此表现的数形结合就是将抽象的数字与小朋友日常生活中比较熟悉的事物联系起来，也就是他们熟悉的“形”，比如1就像铅笔一样是细长的，2的形态就像一只水中的鸭子，3的形态就像耳朵在听声音，4的形状就像彩旗迎风飘，5的形状就像秤钩弯弯的，将“形”与 “数”共同点找出来，这样就将“形”与“数”很好的结合在了一起，以便于小朋友记忆。

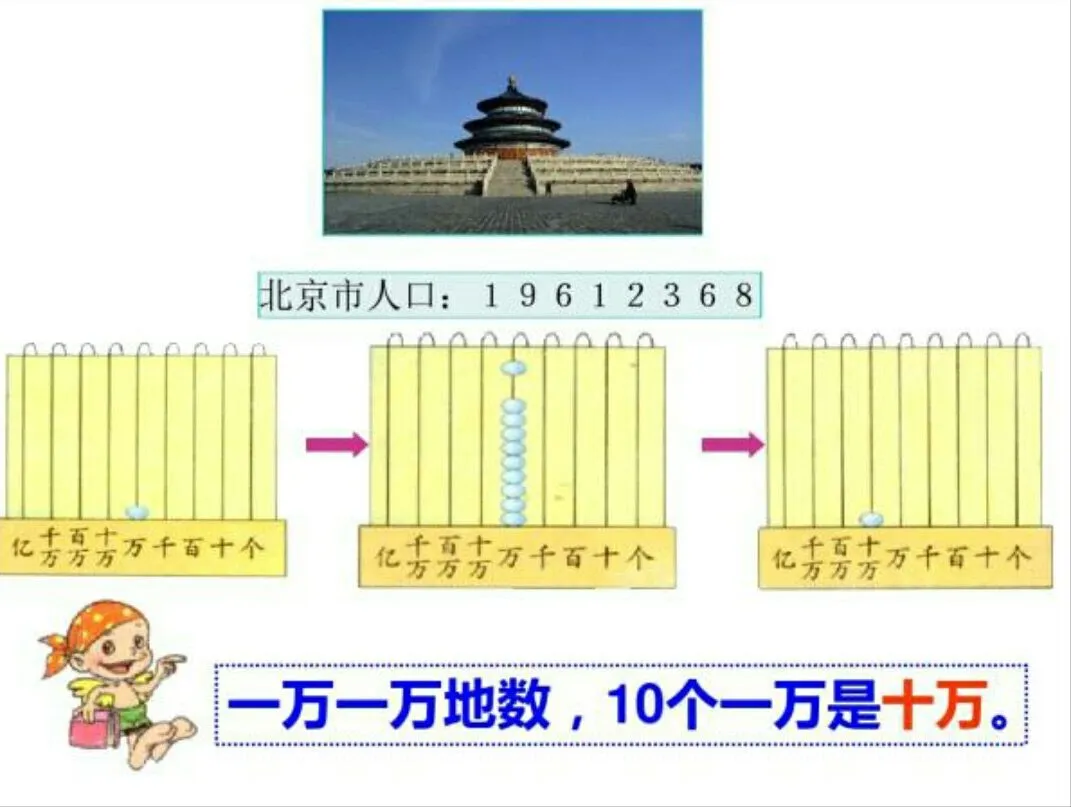
分析：这道题是认识亿以内的数，对我们成年人来说无疑是非常简单的，但是对于小学生而言，他们只知道大数很大，很多，没有具体的概念，这个时候就需要我们把数位在形象的图上表示出来，大数首先从数位上来说就很多，不好读，所以单就读数来看，用图形来读数明显降低了难度，比如，在万位上放一颗珠子，就表示一万，放十颗珠子就表示十万，满“十”就可以进“一”到下一位数位，也就是在十万位上放一颗珠子表示十万，这样图形也帮助小朋友很直观地理解数位。

由上面两道题来看，数形结合在数的认识方面起到了非常直观形象的作用。

（三）数形结合思想体现在关于数的运算

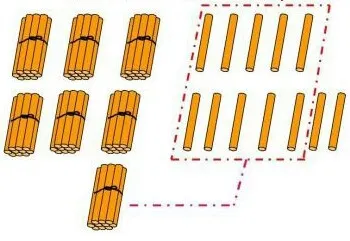
给出的题目是这样的：二（1）班有35人，二（3）班有37人，一共有多少名学生？

列出算式: 35+37

分析：图片中给出的一捆小棒代表的是十，一根小棒代表的是一，35也就是三捆小棒再加五根小棒，37就是三捆小棒再加七根小棒，图片中是将整捆小棒放在一起，也就是有六捆小棒代表60，再将七根小棒拿出五根，余下两根，与旁边的五根小棒放在一起刚好凑成一整捆也就是十，那现在也就是有七捆小棒，代表70，还剩两根小棒，代表2，一共就是72。用一整捆小棒这个“形”来帮助理解进位，让学生直观地认识到“满十进一”的算理，最终会解这个“数”，在这个过程中也是将“数”与“形”有机地结合在了一起。

（四）关于问题解决

例4 小明和余小红两家相距12km，两人同时出发同向而行去少年宫，小红步行每小时4km，小明在后面骑自行车，每小时的速度是小红的3倍，问多久后小明追上小红？

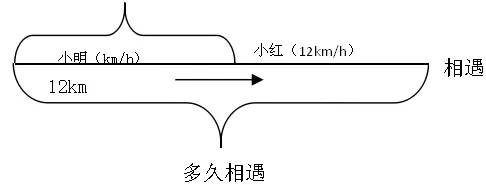
解：小明追上小红，从图中我们可以发现小明比小红多行12km，以这个为切入点进行计算。

小明的速度比小红快 4×3－4=8(km/h)

小明比小红多走12km，即所花时间为 12÷8=1.5（h)

答：一个半小时后邵明追上余伊。

分析：这是一个追击问题，如果直接给学生分析题目，一两句话也解释不清楚，许多同学会觉得乱，这时候可以用画图使题目清晰，追击问题是小学数学应用题中一个重要板块，它可以变化各种各样的形式，且难易各异。解决这类问题，好的逻辑思维能力非常关键，但由于题中信息量的原因，很容易让人搞不清头绪。线段图的出现即简单描述了情境，又将重要信息标注在上面，就本题而言，线段图帮助学生找出等量关系，如“小明比小红多行12km”，从而列出等式。

例5 张建在班级的读书角借了一本书，这本书一共有300页。一段时间后陈新也想看这本书，可他只看了书的2/5，剩下的部分如果要在6天内看完，然后把书给陈新，张建平均每天要看多少页？

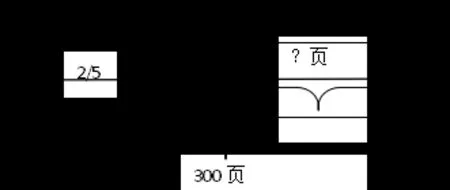
解：1-2/5=3/5 300*3/5=180（页），180÷6=30（页/天）。答：张建平均每天要看30页。

分析：这样的现象在小学是非常常见的，小朋友们常常喜欢看同一本书，遇到类似的问题你能巧妙地解决吗？其实就是把学生生活中的问题转化为数学问题，动员大家思考讨论，看看能否解决。线段图只是将数学信息具体化的一种方式，这种数转化为形最大的好处就是直观具体，从小学就开始培养数形结合的意识，有利于学生养成这样的习惯，今后即使遇到更加复杂的问题时也不至于手忙脚乱，有更多的思路去解决。

三、总结、启示

由以上“数形结合”思想在小学数学教材中的应用分析来看，教材中很多地方都用到了这种数学思想，从低段到高段的教材中均有渗透，这就说明了“数形结合”是小学阶段的一个重要手段，今天我所分析的只是一些初步的、浅显的认识，从长远来看，这一重要数学思想势必对学生们今后在初、高中的学习构建空间思维将起着关键作用。合理、巧妙地在小学数学教材中应用“数形结合”思想，不仅可以为教材的编排深度开辟一片广阔的天地，紧跟新课标改革的步伐，还能为学生的终身学习和可持续发展奠定扎实的基础。