基于蒙特卡罗射线追踪的航天器空间环境因素暴露通量统一计算方法

焦子龙，胡松林，姜利祥，黄建国，孙继鹏，朱云飞

（1. 可靠性与环境工程技术重点实验室； 2. 北京卫星环境工程研究所：北京 100094）

0 引言

航天器在轨运行过程中，受到太阳辐射、轨道残余大气、带电粒子辐射、微流星体及空间碎片等空间环境因素的影响，导致分系统或航天器性能下降，甚至任务无法完成[1]。虽然人们对空间环境因素及其效应的认识有了长足进步，但随着航天器复杂度不断提高，新技术应用比例不断增长，受空间环境影响而发生的故障仍不断涌现。对国外航天器故障进行统计分析发现，主要分系统故障原因都包含空间环境因素的影响[2-3]。同样，对国内遥感卫星和CAST968平台卫星的故障统计发现，归因于空间环境效应的故障分别占其故障总数的38%[4]和46%[5]。因此，开展空间环境效应仿真分析，了解故障机理，是极为必要的。并且，空间环境效应仿真可减少物理试验成本，提高航天器研制效率。

美国、欧空局等开展了大规模的空间环境研究项目，并将研究成果及数据集成为软件工具系统，包括SPENVIS[6]、The Environment WorkBench（EWB）[7]、Space Radiation[8]以及 Geospace Environment Data Analysis System（GEDAS）[9]等。航天器空间环境效应分析必须结合空间环境模式和航天器自身参数，因此各分析系统均集成有航天器轨道计算、环境计算、效应计算等模块，用户只需要输入相关参数，即可计算评估空间环境因素对航天器造成的危害程度。

国内也研制出多种单一空间环境因素效应分析工具或方法，如原子氧通量分析[10-11]、污染分析[12-13]、微流星体及空间碎片分析[14-16]等。这些软件均与国外同类软件进行了对比验证，结果符合较好。但国内目前尚无与国外类似的集成分析工具。

空间环境效应分析的首要条件是获取空间环境因素暴露通量。本文对基于蒙特卡罗方法的原子氧、微流星体、太阳光压、气动力、辐射剂量、材料放气污染等空间环境因素暴露通量的计算方法进行分析总结，提出一种基于蒙特卡罗射线追踪的空间环境因素暴露通量统一计算方法；介绍该算法的计算流程，并针对原子氧通量、大气阻力系数、太阳光压、等效辐射屏蔽厚度等进行计算，与理论值或文献值进行对比验证。

1 空间环境因素暴露通量计算方法分析

航天器空间环境效应包括原子氧剥蚀、大气阻力、总剂量效应、单粒子效应、颗粒高速撞击、光压摄动、表面充电等。为对这些效应进行精确分析，首先需要获得航天器表面遭受的空间环境因素暴露通量。

1.1 原子氧通量计算方法

波音公司建立了基于射线追踪的航天器原子氧通量计算方法及软件[17-20]。计算中，考虑了航天器表面几何形状及相对位置造成的遮挡影响，以及原子氧与表面相互作用发生的镜面反射、漫反射、表面复合、剥蚀等行为的影响。

1.2 微流星体撞击通量计算方法

ESA建立了微流星体撞击通量的计算方法和软件ESABASE/Debris[21]。计算中，将微流星体环境模型根据微流星体速度、尺寸等进行离散化，同时将航天器表面离散化，对每个表面单元，采用射线追踪方法计算其遭受的一定速率、一定尺寸的微流星撞击通量，然后累加求和得到航天器整体的受撞击通量。

1.3 气动力计算方法

轨道残余大气分子与航天器发生动量交换产生气动力，是低轨航天器在轨运行除地球非理想球形引力外的其他主要摄动力之一[22]。Fritsche等人建立了气动力计算方法[23-24]。计算中，将大气视为稀薄气体，其分子运动符合自由分子流描述，则气动力计算可以采用试验粒子蒙特卡罗方法：首先根据航天器几何构型设置计算区域（长方体），模拟试验粒子在区域内的运动，当试验粒子与航天器表面碰撞时，与表面按照一定的表面作用模型进行动量交换，并从表面反射；计算粒子与表面的动量交换，然后以反射点为起点，继续追踪粒子的运动，直到粒子逸出计算区域为止；通过模拟大量的粒子运动，可以统计得到航天器所受大气气动力参数。

1.4 太阳光压计算方法

太阳光压计算可采用与气动力计算类似的方法[23-24]：首先设置计算区域（长方体），根据太阳入射方向得到计算区域各面的太阳辐射通量；然后从计算区域各面随机选取位置作为入射光束的起点，光束方向为太阳入射方向，光束代表的太阳辐射通量由蒙特卡罗抽样总数计算，计算光束与卫星表面部件的交点，并判断距离最近的交点，其所在面元即为实际受太阳光照射的面元；计算在该面元上产生的太阳光压，如果该面元的镜面反射率大于0，则按照上述流程继续追踪反射光线的运动，并计算其产生的太阳光压；循环上述过程，直到反射光线强度小于规定的阈值时停止。

1.5 辐射剂量计算方法

国内外开发了多种三维辐射剂量评估方法和软件[25-29]。由于航天器结构为薄壁结构，吸收剂量计算中采用了近似直线传输原理[30]，即入射高能粒子在材料中沿直线运动，因此屏蔽厚度采用沿入射方向直线上的结构厚度，即若高能粒子入射方向与结构表面法线间的夹角为θ，则屏蔽厚度Leあ=L/cosθ，其中L为结构厚度。基于此原理，吸收剂量的计算过程为：在星内选定辐射剂量分析点，从该点向星外全向空间均匀分布引出若干条射线；然后计算出每条射线穿透的卫星中各仪器设备、结构件等单元的累积屏蔽厚度；再结合剂量-深度关系曲线，计算得到每条射线所代表的小区域中经屏蔽后的空间辐射剂量，从而完成整星辐射剂量三维分析计算。

1.6 放气污染计算方法

在轨航天器用有机材料造成的表面污染量及性能退化程度计算方法为[31-32]：认为放气分子发射及分子从表面反射均符合余弦规律，放气点位置在放气表面元均匀分布，利用蒙特卡罗方法抽样放气分子运动的起始位置和方向；然后抽样分子运动的自由程，判断该自由程代表的分子运动路程是否与物体表面相交，没有经历碰撞的情形可以认为自由程为无穷大；从大量的分子运动轨迹中抽样计算得到污染源i和目标表面j之间的质量传递系数，将其代入矩阵方程即可求解得到表面j的入射流，则该表面的沉积速率为，其中为该表面污染分子的沉积系数。

2 空间环境因素暴露通量统一计算方法的提出

空间环境效应分析是卫星设计研制中的一项重要工作，呈现出不同空间环境因素效应协同分析以及与卫星任务级、系统级分析集成等发展趋势。为此，本文提出构建统一的基于蒙特卡罗射线追踪的计算方法，将原子氧、微流星体、带电粒子、放气分子等视作模拟粒子，用射线代表粒子的运动轨迹，追踪大量粒子与航天器表面的相互作用，从而得到原子氧通量、微流星体撞击通量、气动力、太阳光压、辐射剂量、放气污染量等。相比于单空间环境因素效应分析工具，这种计算方法物理图像清晰，无须航天器几何模型在不同分析工具之间的转换，可显著提高分析评估的效率，有助于未来实现任务级、系统级集成分析。

3 空间环境因素暴露通量统一计算方法流程

本文提出的基于蒙特卡罗射线追踪的统一计算方法流程如图1所示。主要步骤如下：

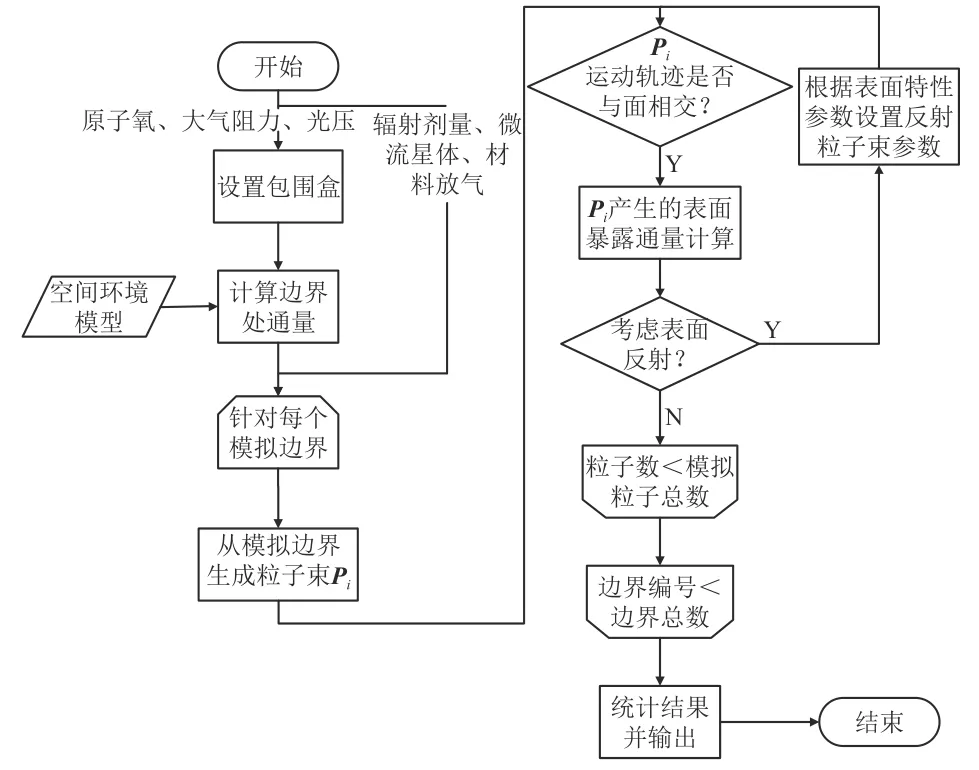
图1 航天器空间环境因素暴露通量计算流程Fig.1 Flowchart for exposure flux computation of space environmental factors

1）构建航天器三维模型，划分表面网格。根据三维模型设置长方体包围盒，作为模拟边界。

2）设置环境因素模型参数。根据计算精度等要求设置模拟粒子数等其他全局参数。

3）对于原子氧、大气阻力、太阳光压暴露通量，基于空间环境模型计算边界处通量。例如，对于原子氧，采用NRLMSISE-00模型[33]得到某轨道位置的大气原子氧数密度nO、温度T等参数值，则模拟边界处单位面积上的原子氧通量为

4）从模拟边界处生成代表粒子的射线。对于原子氧、大气阻力、太阳光压计算，模拟边界为人为设置的包围盒表面；对于辐射剂量、微流星体、材料放气计算，模拟边界为航天器表面单元。射线起点位置P0在边界上均匀随机分布，射线方向D按照环境因素特性随机抽样。射线可表示为

5）追踪射线，判断其轨迹与表面是否相交。如果相交，根据其与航天器表面的相互作用模型计算暴露通量；然后根据表面特性重新设置射线的方向，并以交点为新的起点；继续追踪，直到射线逃逸出限定计算区域，或者满足一定的阈值条件后抛弃该轨迹。若不相交，则进行下一个粒子的模拟。

6）对所有边界进行模拟后，统计得到暴露通量，并输出计算结果。

4 空间环境因素暴露通量统一计算方法的仿真校验

空间环境因素暴露通量统一算法的校验可通过将统一算法计算结果与理论值（或文献值）进行对比完成。复杂几何构型航天器难以获得理论值，且已有文献中航天器构型复杂、难以精确复现。为此，本文采用典型简单几何模型作为模拟对象，将统一算法的计算结果与理论值进行比对：以航天器几何模型划分的表面网格作为基本模拟单元，考虑几何模型的代表性，选取文献[32]中的圆盘算例作为模拟对象，圆盘直径0.564 m，划分三角形网格；统一算法的模拟误差与模拟粒子数目N的平方根成反比，由于圆盘为简单几何模型，计算量较小，所以选取模拟粒子数目为100万个。

4.1 原子氧暴露通量

计算圆盘不同攻角下的原子氧暴露通量。理论分析值取自文献[17]，轨道原子氧数密度8.2×1011/m3，圆盘速度8000 m/s。粒子撞击速度分布采用舍选抽样法[34]，撞击位置在包围盒表面上均匀随机分布。原子氧暴露通量的计算值和理论值对比如图2所示。由图可见：攻角为0°～80°时，计算值与理论值间的相对误差小于0.1%；攻角为90°时，相对误差为1%，计算值和理论值符合很好。但误差随攻角的变化规律有待进一步研究。

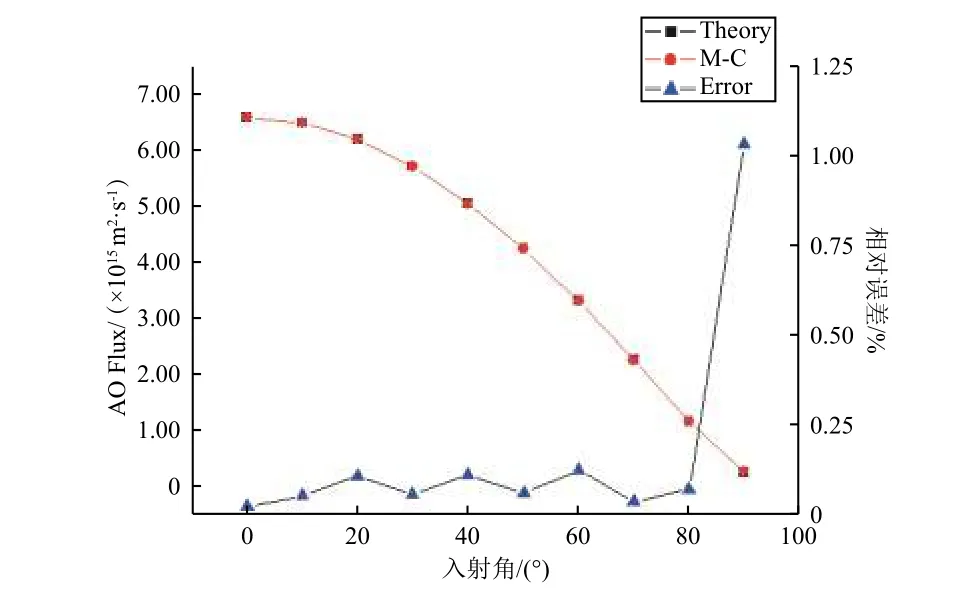
图2 圆盘算例原子氧暴露通量理论值与计算值比较Fig.2 Comparison of theoretical and calculated AO fluxes for circular disk sample

4.2 大气阻力

大气阻力可表示为[35]

式中：CD为大气阻力系数；A为迎风面面积；ρ为大气密度；vr为航天器相对于大气的运动速度；ev为航天器相对大气运动方向单位矢量。航天器轨道、姿态一定时，其大气阻力取值主要与大气阻力系数CD有关，而影响CD的主要因素是气体分子与航天器表面相互作用模型。本文分别采用镜面反射模型和漫反射模型计算3.1节中圆盘算例的大气阻力系数。理论分析值取自文献[35]，圆盘表面温度为300 K。大气阻力系数的计算值与理论值对比如表1所示，2种反射模型下计算值与理论值间的相对误差均仅有0.1%，二者符合较好。

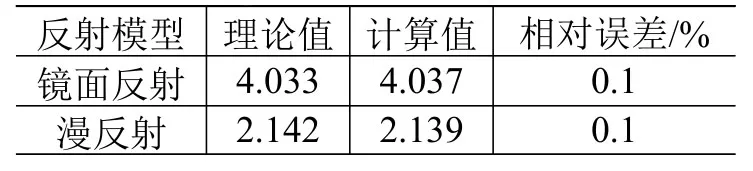
表1 大气阻力系数计算值与理论值对比Table 1 Comparison between theoretical and calculated values of drag coefficients

4.3 太阳光压

太阳光压可表示为[36]

式中：c为真空中的光速；Φ为单位时间单位面积接受的太阳辐照度，其在地球表面的平均值约为1367 W/m2，随卫星与太阳间距离不同而变化，变化幅度为每年±3.3%。不同太阳光入射角下的太阳光压计算值与理论值对比如图3所示。从图中可以看出，计算值与理论值间的最大误差约为0.4%，二者符合较好。

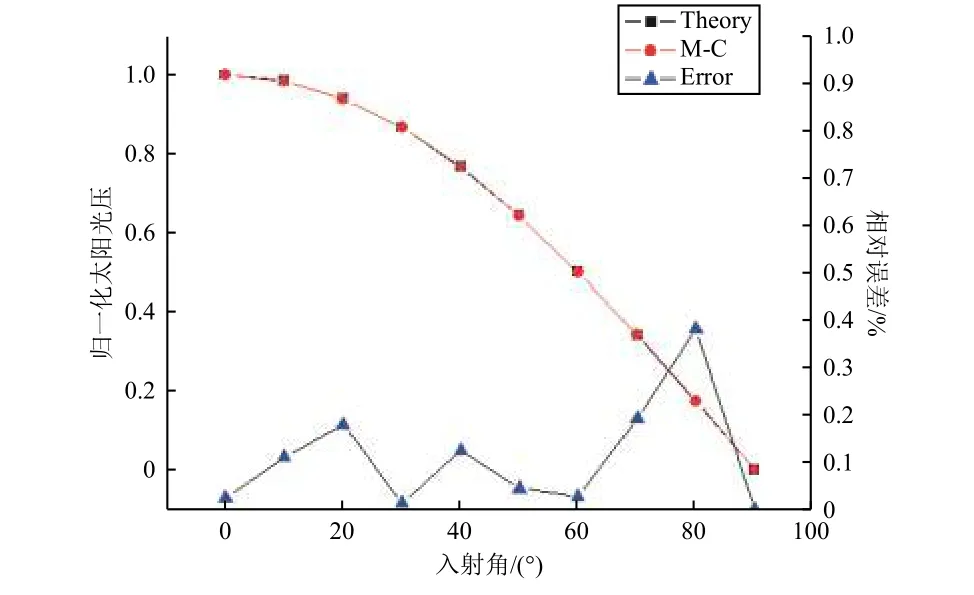
图3 不同太阳光入射角下的归一化太阳光压计算值与理论值对比Fig.3 Comparison between theoretical and calculated value of normalized solar pressure for different incidence angles

4.4 微流星体撞击通量

微流星体撞击航天器表面的撞击通量可以表示为

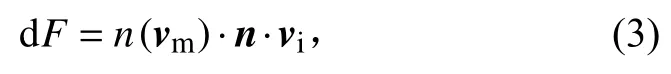
式中：vi为微流星体撞击速度，是微流星体相对于航天器的速度，vi=vm-vs，vm为微流星体速度矢量，vs为航天器速度矢量；n(vm)为微流星体速度分布。文献[21]给出了当所有微流星体具有相同速度，即n(vm)=1时，航天器速度矢量与表面法线呈不同角度时，其微流星体归一化撞击通量的变化。图4给出了统一算法计算结果与文献值的对比。由图中可以看出，计算值与文献值间的误差最大约0.4%，二者符合较好。

4.5 等效辐射屏蔽厚度

用统一算法对文献[27]中边长400 mm、厚度3 mm的空心铝质立方体的屏蔽厚度进行计算，得到其等效屏蔽厚度为3.55 mm，与文献值一致。空心铝质立方体等效屏蔽厚度分布如图5所示。从图中可以看出，正方体8个顶点处等效屏蔽厚度较大，接近5.2 mm；而中心处等效屏蔽厚度较小，为3 mm，符合几何形态规律。

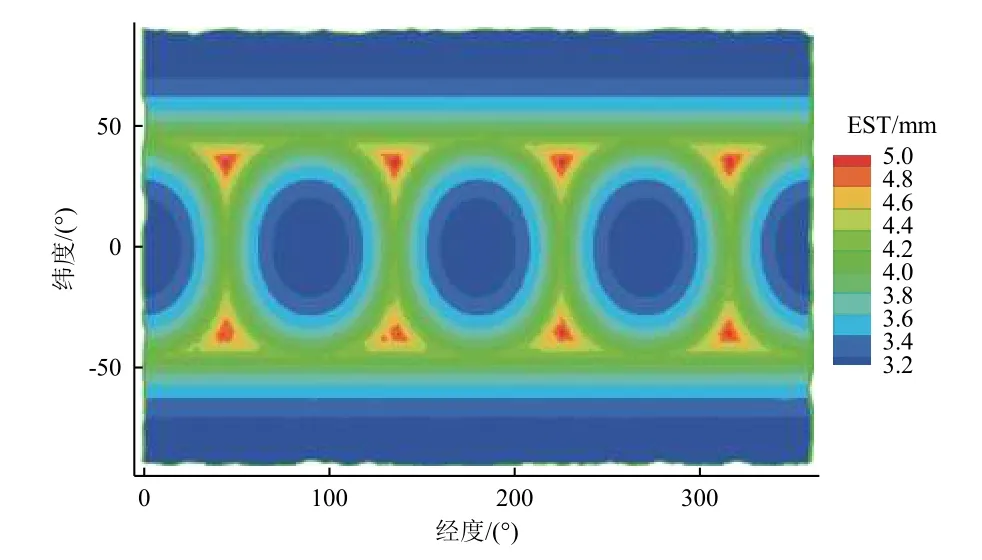
图5 空心铝质立方体等效屏蔽厚度分布Fig.5 Distribution of equivalent shielding thickness of hallow aluminum cube

4.6 分子污染返回流

利用统一算法进行圆盘放气污染返回流的计算，结果为 1.33×10-6，与文献值[32]相比，相对误差为0.3%，二者符合较好。

5 结论

本文提出了一种基于蒙特卡罗方法的空间环境因素暴露通量统一计算方法：将空间环境因素等价为粒子束或能量束集合，用射线代表粒子束或能量束，跟踪射线在空间中的运动以及与航天器表面的相互作用，得到空间环境因素暴露通量。针对简单几何构型，通过典型算例（圆盘）计算了原子氧暴露通量、大气阻力系数、太阳光压、微流星体撞击通量、等效辐射屏蔽厚度、分子污染返回流等，与理论值进行对比，均符合较好，证明本文提出的统一算法能够正确模拟相关物理过程，可用于近地轨道、深空等各种航天器的空间环境因素暴露通量计算。

利用统一算法的计算过程中，仅对表面划分一次网格，即可用于多种空间环境因素暴露通量的计算，因此对于复杂构型航天器，可显著节省几何模型建模时间，提高空间环境效应分析效率，便于与其他系统级、任务级分析软件集成。

下一步将利用真实在轨或地面试验数据对该方法进行对比验证分析，以检验其有效性。