基于改进混合作用力微粒群算法的液压阀块加工车间调度优化

陈东宁， 彭晓静， 姚成玉3， 张晓磊3， 杨晓荣

(1. 燕山大学河北省重型机械流体动力传输与控制重点实验室， 河北秦皇岛 066004; 2. 先进锻压成形技术与科学教育部重点实验室(燕山大学)， 河北秦皇岛 066004; 3. 燕山大学河北省工业计算机控制工程重点实验室， 河北秦皇岛 066004)

引言

车间调度是先进制造系统的重要环节，直接影响企业的效益和竞争力。车间调度指产品加工过程中，在最大限度满足各种约束条件下，通过合理地安排各种资源及加工的先后顺序，减少零件完工时间，从而提高企业车间的生产效率[1]。车间生产中，不合理的作业生产安排会导致不必要的生产能耗，因此，制定合理的调度方案显得尤为重要[2]。近年来，微粒群算法在解决车间调度问题中取得了较好的效果。微粒群(Particle Swarm Optimization, PSO)算法[3]作为一种高效智能优化算法，凭借结构简单、收敛速度快、参数设置少等优点，成功应用于各种复杂优化问题。例如，文献[4]将提出的多作用力微粒群算法用于求解液压阀块加工车间调度问题；文献[5]利用改进的二阶微粒群算法优化了具有空闲时间的车间调度问题；文献[6]针对柔性作业车间调度问题，提出一种骨干双粒子群算法。

PSO算法已成功解决各种车间调度问题，但在作用力规则方面，标准PSO算法中仅考虑个体最优微粒和全局最优微粒的引力作用，易使算法陷入局部最优。为此，许多学者从作用力方面对PSO算法进行了改进研究。例如，文献[7]将微粒群分为多个子群，每个子群中适应度最差的2个微粒与其他子群的微粒学习交流；文献[8]算法初期充分发挥全局最优解的领导能力，中后期利用随机化均匀扰动粒子改变群体的作用力规则；文献[9]将微粒仅受其他微粒吸引的作用方式，扩展为微粒受比自身适应值优的微粒的吸引，同时受比自身适应值劣的微粒的排斥；文献[10]通过引入中间适应度微粒的引力作用，为微粒逃离局部最优解提供动力。

综上可见，上述改进的PSO算法从避免算法早熟收敛、保证种群多样性和提高收敛速度等某些侧面进行改进，但这些算法仅考虑到单种的作用力规则，不能同时满足种群多样性和收敛速度的要求。为此，针对在不同的搜索阶段采用不同的作用力规则，平衡算法全局探索性搜索和局部趋化性搜索能力，提出改进混合多作用力微粒群(Improved Hybrid Force PSO,IHFPSO)算法，进而将其用于液压阀块加工车间调度问题，由所提算法优化得到的阀块加工顺序和每道工序机器的分配情况，确定最佳的调度方案，解决基于人工排序产生的原有调度方案时间长的问题。

1 改进的混合多作用力微粒群算法

IHFPSO算法的思想是：算法采用阶段性搜索策略，将算法的搜索过程分为前期和后期2个搜索阶段。在前期搜索阶段，微粒受到所有个体最优解的影响，同时考虑微粒受到的“吸引”和“排斥”作用，构建微粒间作用的引斥力规则；在后期搜索阶段，改变当前微粒的学习对象，引入全局最优解、个体最优解的平均值对当前微粒的吸引作用，同时构造基于动力加速度的引力规则，使微粒在双作用力和引力提供的加速度的作用下进行速度和位置的更新，满足种群多样性和收敛速度的要求，平衡算法的全局探索和局部搜索能力。

IHFPSO算法的速度和位置的更新公式为：

β(wx×[pavg-xid(t)]+(1-wx)×

cgrg[pgd(t)-xid(t)])

(1)

(2)

式中，vid(t+1)，vid(t)为微粒i第t+1代与第t代的第d维速度；xid(t+1)，xid(t)为微粒i第t+1代与第t代的第d维位置；pjd(t)为微粒j第t代个体最优解的第d维位置；pgd(t)为第t代全局最优微粒g的第d维位置；pavg为比微粒i适应值好的个体最优解的平均值；B(i)为个体最优解比微粒i适应值好的集合；W(i)为个体最优解比微粒i适应值差的集合；aid(t)为微粒i第t代第d维的动力加速度；cj，cg为加速常数；rj，rg为(0, 1)区间内相互独立的随机数；α，β为前、后期的切换系数；w为惯性权重；wx为动态权重。

个体最优解的平均值可由式(3)求得：

(3)

式中，pkd为微粒i邻域微粒k的第d维的位置；K为微粒i邻域微粒的个数；N(i)为微粒i邻域微粒的集合。

在标准PSO算法中，微粒在个体经验和群体经验的指导下向更好的位置移动，将速度更新公式中的个体认知项和社会认知项看作加速度项，为微粒的搜索提供动力，则当前微粒i第d维的动力加速度aid(t)定义为：

aid(t)=rj(pid(t)-xid(t))+

rg(pgd(t)-xid(t))

(4)

惯性权重w可由式(5)求得：

(5)

式中，wmax为惯性权重值上限；wmin为惯性权重值下限；tmax为最大迭代次数。

算法前期、后期两搜索阶段的切换系数α，β可分别由式(6)、式(7)求得：

(6)

(7)

式中，γ为记录搜索前期算法进化停滞的次数；γmax为设置的算法进化停滞次数阈值。

算法进化停滞是指全局最优微粒的适应度在连续若干代内不发生变化，γ由式(8)计算得到：

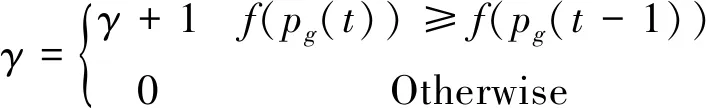
(8)

动态权重wx可由式(9)求得：

(9)

式中，tx为算法前期向后期切换的迭代次数。

在算法搜索后期，随着迭代次数的增大，动态权重wx线性递减，全局最优解的吸引作用线性增大，既强化了算法的局部搜索能力，又能有效降低微粒陷入局部最优的概率。

2 液压阀块加工车间调度优化

2.1 液压阀块加工车间介绍

某公司液压阀块加工车间主要为动力站中的泵站单元和阀台单元提供用于安装各种液压元件并实现各元件油路连通的阀块。该阀块加工车间第1道工序有1台锯床，用于完成坯料的落料；第2道工序由两台铣床来完成各加工面的粗铣；第3道工序有1个卧式数控加工中心，能够完成批量阀块的所有阀孔和孔道的加工，有3台摇臂钻床，能够完成划线和除特殊阀孔以外的阀孔加工；第4道工序有2台去刺机，可完成各阀孔棱角倒钝、去毛刺的工作；第5道工序有1个立式数控加工中心对阀块的安装面进行精铣；第6道工序有2台打码机，可完成阀块出口处打钢印的工作。

该调度方案依据各机器的加工能力和现场经验，采用人工排序的方法产生，其调度指标(最大完成时间)Cmax=525 min。

2.2 阀块加工车间调度优化模型

由上述车间介绍可知，该液压阀块加工车间调度问题属于混合流水车间调度问题(Hybrid Flow-shop Scheduling Problem,HFSP)，HFSP可描述为：n个工件要经过S道工序以完成加工，每道工序至少有1台机器进行加工且至少有1道工序存在并行机，同1道工序上各机器的处理性能有所不同，工件要经过所有工序的加工，但各工件的每道工序可在任意1台并行的机器上加工，已知工件在各工序相应机器上的处理时间，确定工件的加工顺序和每道工序机器的分配，使得调度指标最小。

这里假设：工件一旦开始加工便不可中断；1台机器同一时刻只能加工1个阀块；1个阀块同一时刻只能在1台机器上加工。考虑各机器的调机时间，以完成n个阀块加工的最大完成时间最小为目标，给出该阀块加工车间调度优化模型为：

minCmax=max{C1,C2, …,Cn}

(10)

约束条件由式(11)～式(16)给出：

(11)

(12)

(13)

eijk≤sij+1k′

i=1, 2, …,n;j=1, 2, …,S-1;

k=1, 2, …,mj;k′=1, 2, …,mj+1

(14)

i=1, 2, …,n;l=1, 2,…,n-1;

k=1, 2,…,m1

(15)

l1,l2=1, 2,…,n;l1≤l2;

j=1, 2, …,S;k,k′=1, 2, …,mj

(16)

阀块i第j道工序在第k台机器上的完成加工时间eijk与处理时间tijk可由式(17)、式(18)求得：

eijk=sijk+tijk

(17)

tijk=stijk+ptijk

(18)

式(10)～式(18)中，Ci为阀块i的加工完毕时间；n为阀块总数；Cmax为完成n个阀块加工的最大完成时间；xil为取值为1或0的常数，若阀块i在第l个位置上加工为1，否则为0；yijk为取值为1或0的常数，若阀块i的工序j在k台机器上为1，否则为0；mj为阶段j的机器数；S为阶段总数；sijk为阀块i第j道工序在第k台机器上的开始加工时间；stijk为阀块i第j道工序在第k台机器上的调机时间;ptijk为阀块i第j道工序在第k台机器上的加工时间。

上述调度优化模型中，式(11)、式(12)确保了同一时刻机器与阀块间的一一对应；式(13)使得每道工序每个阀块只能在1台机器上加工；式(14)表示同一阀块不同工序间的先后制约关系；式(15)完成了第1道工序上调度排列中排位越前的阀块开始加工时间越早；式(16)实现了分配在同一机器上的阀块排位靠后的必须等靠前的加工完毕才可进行加工，当处于不同位置的阀块不在同道工序的同一机器上加工时，L为数值较大的常数以保证不等式恒成立。

2.3 液压阀块加工车间调度IHFPSO优化

采用IHFPSO算法求解液压阀块加工车间调度问题。首先，利用矩阵变量来处理约束条件，对微粒进行编码；然后，利用IHFPSO算法不断地搜索并更新全局最优解；最后，对微粒进行解码，求得最优的调度方案。

现有8个阀块要加工，每个阀块均需经过6道工序：落料、粗铣、钻、去毛刺、精铣、打钢印，阀块在各机器上的加工时间如表1所示。

1) 微粒编码

利用矩阵对微粒进行编码，矩阵的元素来表示机器，矩阵元素的位置关系来表示优化模型中工序间的约束关系，为了扩大微粒的搜索空间，采取随机产生实数的编码方法，以均等的机会选择机器。

假设加工需要S道工序的n个阀块，每道工序的机器数为mj(j=1, 2, …,S)，对所有机器按照加工工序依次排序编号，可构造一个编码矩阵AS×n为：

(19)

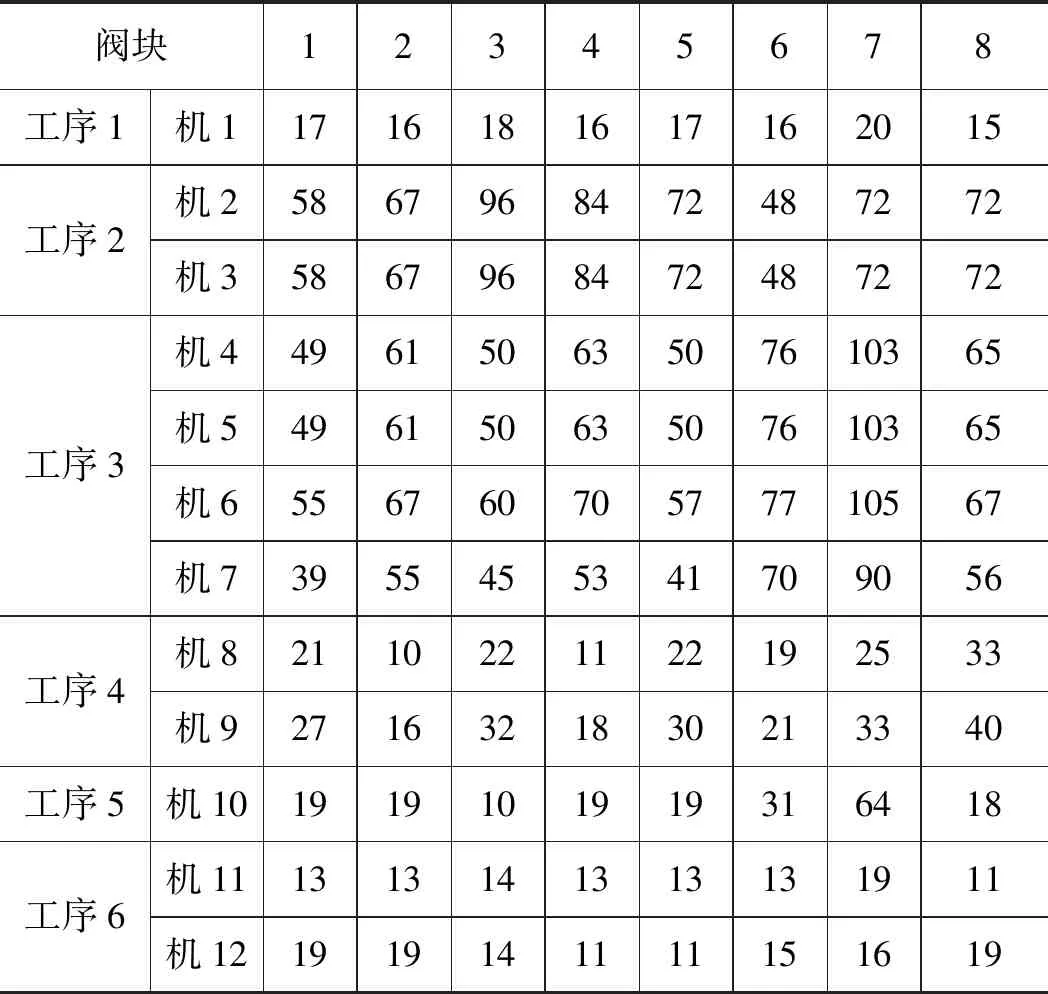
表1 阀块在各个机器上的加工时间 min

对微粒进行编码：每个微粒由S个小段组成，每个小段包括n个数值，每个微粒对应一个可行的调度方案。采用图示的方式描述自变量aji与位置矢量Xi的元素之间的对应关系，如图1所示。

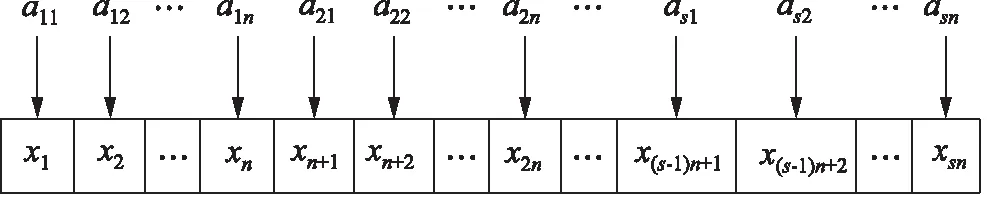
图1 微粒编码图示

根据上述微粒编码方法，对于该液压阀块加工车间调度优化问题，自变量aij与位置矢量Xi的元素之间的对应关系如图2所示。

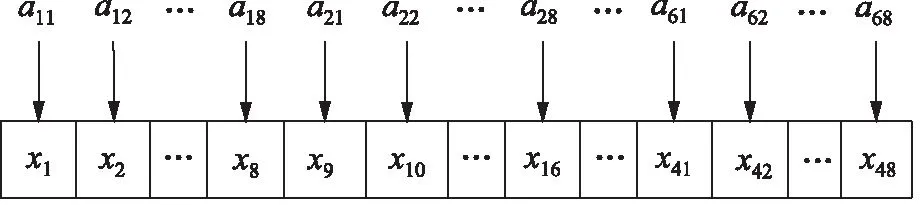
图2 该液压阀块微粒编码图示

采用IHFPSO算法求解该液压阀块加工车间调度问题，其参数设置为：种群规模N=20、函数维数n=8×6=48、最大迭代次数tmax=500、惯性权重w=0.9～0.4、加速常数cj=cg=1.49。则微粒i经过500代搜索后得到一个编码矩阵A为：

(20)

2) 微粒解码

采用矩阵的解码方式，得到选择机器矩阵；然后将液压阀块在各机器上的加工时间生成加工时间矩阵，按照阀块的加工排序规则，得到完成时间矩阵。对式(20)的编码矩阵A进行解码。

(1) 将编码矩阵A中各个元素分别向下取整得矩阵B为：

(21)

由矩阵B可得到各阀块与机器的对应关系，例如，阀块1的6道工序分别在机器1、3、4、8、10、11上加工；阀块2的6道工序分别在机器1、3、6、8、10、12上加工。

将6×8的矩阵B扩充为12×8的选择机器矩阵S，基于各阀块选择机器的情况，置相应行(表示机器)的元素为0或1，0表示没有选择该机器，1表示选择该机器。由此可得到选择机器矩阵S为：

(22)

(2) 为表示阀块在其对应加工机器上的使用时间，根据选择机器矩阵S，结合表1中各阀块在各机器上的加工时间，得到加工时间矩阵Tt，它表示各阀块的各道工序在其选择的机器上的加工时间：

(23)

(3) 根据阀块加工顺序规则，由加工时间矩阵可确定同一机器上阀块的加工先后顺序。机器1加工阀块8、6、7、2、1、5、3、4的第1道工序；机器2加工阀块6、7、5、4的第2道工序；机器3加工阀块8、2、1、3的第2道工序；机器4加工阀块1的第3道工序；机器5加工阀块6、3的第3道工序；机器6加工阀块8、2、5的第3道工序；机器7加工阀块7、4的第3道工序；机器8加工阀块6、2、7、1、5、4的第4道工序；机器9加工阀块8、3的第4道工序；机器10加工阀块6、8、2、7、1、5、4、3的第5道工序；机器11加工阀块8、7、1、3的第6道工序；机器12加工阀块6、2、5、4的第6道工序。

根据阀块加工顺序规则和加工时间矩阵Tt生成各阀块在所选机器上的完工时间矩阵Tz：

(24)

矩阵Tz中元素表示的是相应阀块各道工序在所选机器上完成加工的时间，所以矩阵中元素最大的数即为微粒所表示调度方法的最大完成时间，即Cmax=414 min。

3) 结果对比与分析

将IHFPSO算法用于求解该液压阀块加工车间调度问题，并与车间原有调度方案以及PSO算法、MPSO(中值导向微粒群)算法[10]、EPSO(扩展微粒群)算法[9]、MFPSO(多作用力微粒群)算法[4]的运行结果进行对比，以验证所提算法的有效性。令PSO算法、MPSO算法、EPSO算法与IHFPSO算法的参数设置相同，MFPSO算法的参数设置中，切换因子t1为50、t2为350，其余参数与IHFPSO算法的参数设置相同。上述5种算法独立运行10次的优化曲线见图3，所得优化结果见表2。

图3 5种算法的优化结果曲线

由图3和表2可知，IHFPSO算法所得结果最优，所得的最优调度方案缩短了最大完成时间，故所提的IHFPSO算法是有效、可行的，在车间加工时采用该调度方案，根据阀块的加工顺序和每道工序机器的分配情况，对各阀块进行加工，可提高液压阀块加工车间的生产效率，也有助于实现节能减排、节约成本。

表2 优化结果(最大完成时间)对比 min

3 结论

为平衡算法的全局和局部搜索能力，提出了改进混合多作用力微粒群(IHFPSO)算法，采用阶段性搜索策略，将算法的搜索过程分为2个搜索阶段。在搜索前期，同时考虑微粒受到的“吸引”和“排斥”作用，构建微粒间作用的引斥力规则。在搜索后期，引入全局最优解、个体最优解的平均值对当前微粒的吸引作用，同时构造基于动力加速度的引力规则，满足搜索后期收敛速度的要求，提高算法的寻优能力。将IHFPSO算法用于求解液压阀块加工车间调度问题，并与车间原有调度方案以及标准微粒群、中值导向微粒群、扩展微粒群、多作用力微粒群算法进行了对比，结果表明，提出的IHFPSO算法结果最优，实现液压阀块加工车间调度优化。