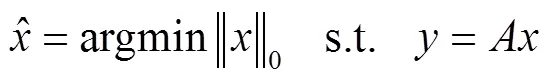基于Dog-Leg正则化自适应压缩采样的植株图像重构

沈 跃，李尚龙，刘 慧，刘加林

基于Dog-Leg正则化自适应压缩采样的植株图像重构

沈 跃，李尚龙，刘 慧※，刘加林

（江苏大学电气信息工程学院，镇江 212013）

目标植株的图像压缩与重构在农作物生长状态检测、田间管理和果树病虫害识别等方面有重要作用。传统的图像压缩感知方法存在重构精度低、时间长等问题。针对这些情况，该文提出一种基于Dog-Leg最小二乘的正则化自适应压缩采样匹配追踪（regularized adaptive compressed sampling matching pursuit based on Dog-Leg，DLRaCSMP）算法。该算法以压缩采样匹配追踪（compressive sampling matching pursuit，CoSaMP）算法为基础，在迭代过程中采用正则化处理，确保支撑集选取的准确性，并结合变步长自适应思想和Dog-Leg最小二乘算法，在实现稀疏度自适应的同时，提高重构速率；选用Kinect获取目标植株的彩色图像，分别采用HSV彩色空间的亮度和色调特征及Sobel算子的轮廓特征输入至Itti模型中融合构建显著性特征图，以简化复杂背景和突出目标植株。试验结果表明，该算法在采样率为0.50时植株原始图像和显著性特征图的重构时间分别为2.14和1.75 s，较CoSaMP算法分别缩短6.57和6.31 s，重构效率比CoSaMP算法平均分别提高75.5%和77.9%；图像峰值信噪比分别高达35.16 和38.93 dB，较CoSaMP算法分别提高6.12 和5.75 dB，且重构精度比CoSaMP算法平均分别提高21.6%和15.5%，可以实现植株图像的快速精确重构。

图像重构；算法；压缩感知；最小二乘法；显著性特征图；边缘检测

0 引 言

图像采集与重构是机器视觉技术发展的关键技术之一[1-2]。近年来，随着农业信息化和自动化的不断发展，图像的压缩重构在农作物生长状态检测、田间管理、植物微环境生理参数采集和果树病虫害识别等方面起到了重要作用[3-6]。当前信息需求量持续增加，信号带宽越来越宽，如何高速率高质量地对图像进行压缩采集并重构已成为研究热点和重点[7-8]。比起香农采样定理对采样率至少达到原始信号带宽2倍以上的要求[9]，采样与压缩并行的压缩感知理论有效地克服了传统采样定理高采样率的缺陷，为信息的传输提供了新的途径[10]。

在农业植株的检测与识别过程中[11]，目标对象的识别是首要解决的问题。Itti等[12]提出的自下而上的显著性模型，通过初级特征的提取，获取显著性特征图，从而彰显目标物体，但是提取效果并不突出。高超等[13]针对植株微环境及生理参数在ARM（advanced RISC microprocessor）平台上设计了基于压缩感知的采集算法，在节省数据存储空间和降低数据传输量的同时，一定程度上也降低了系统的功耗，但是对于不同尺度和背景下的植物信息采集并没有验证。代媛等[14]提出了一种压缩感知苹果图像的并行快速重构方法，该算法分析了二维正交匹配跟踪重构算法的并行性，结合GPU通用并行计算平台设计出对应的并行化重构算法，初步提高了苹果图像的重构效率，但是并没有保证苹果图像的重构质量，且未能消除复杂背景。廖勇等[15]提出了一种变步长正则化自适应压缩采样匹配追踪算法，该算法改进了稀疏度自适应匹配追踪算法（sparse adaptive matching pursuit，SAMP）固定步长带来的精度不够以及过度估计问题，一定程度上提高了重构方法的重构精度，但在迭代优化上仍沿用最快下降算法，在求解函数时，存在过于贪婪导致收敛速度较慢，重构效率不高。

本文在前人研究基础上，通过Kinect V2.0获取植株RGB图像，并将其转换成HSV色彩空间获得植株亮度图和色调图，采用Sobel边缘检测算法获得植株轮廓图，最后把3幅图输入至Itti模型中进行融合得到植株显著性特征图；算法上以压缩采样匹配追踪（compressive sampling matching pursuit，CoSaMP）算法为基础，在候选原子集时采用正则化处理，再利用回溯思想对其进行筛选，迭代优化过程中，采用Dog-Leg最小二乘算法加快收敛速度，再比较相邻重构过程获得的残差值大小，设定相对阈值调整步长，通过大步长快速接近，缩短重构时间，小步长精确逼近保证重构精度，从而实现信号快速并精确地重构。

1 压缩感知与重构算法

1.1 压缩感知理论基础

压缩感知理论主要由稀疏表示、测量矩阵和重构算法[16]三部分组成。稀疏表示是压缩感知的先验条件，常用的稀疏基有离散余弦变换基（discrete cosine transform，DCT）[13]、Curvelet基[17]、Gabor基[18]以及冗余字典[19-20]等。测量矩阵需要满足等距约束性条件[21-22]才能精确重构原始信号。重构算法是压缩感知中最为关键的一部分，也是本文的研究重点。

得到观测值之后，根据稀疏重构关系，通过合适的重构算法可以实现信号的重构。理论证明，采用最小0范数方法求解可以获得稀疏解