数字图像相关的多尺度图像子区匹配算法

林 哲，蔡 恬，王燕锋

（1.汕头职业技术学院计算机系，广东 汕头 515078；2.汕头职业技术学院网络与信息中心，广东 汕头 515078；3.中原工学院建筑工程学院，河南 郑州 450007；4.汕头大学工学院，广东 汕头 515063）

0 引 言

自1980 年以来，数字图像相关（DIC）被广泛用于测量固体表面的位移和应变[1-4]，它是一种重要的非接触式光学实验方法.通常的做法是用一台固定的数码相机在试件变形前后的瞬间对其表面拍摄两次照片，这两张图像分别称为参考图像和变形图像，然后用计算机算法对它们进行处理，确定表面上每个点的相对位移.为了计算参考图像与变形图像之间点与点的关系，基于图像子区（subset）的方法在实践中得到了广泛的应用.对于变形图像中的每一个点，利用其周围区域的局部信息（即图像子区）对参考图像中的最佳对应点进行跟踪.

在过去30 年里，为了提高基于图像子区的DIC 的精度和效率，人们做了大量的工作.例如，Schreier 等利用高阶样条插值函数实现了0.01 像素的测量精度[5]，并且分析了因形状函数匹配不足而产生的系统误差，研究了非均匀应变场匹配过程中的二阶形状函数[6].Cheng 等人提出了一个高效、准确、健壮的框架.采用均匀参数b 样条曲面函数.通过迭代优化，将整个试件表面积表示为未知的二维变形场[7].此外，关于搜索过程[8-9]、相关方法[10-11]、配准方法[12-18]、测量精度[19-21]、可靠性[22-24]、计算速度[22-29]等方面研究也有很多报道.

目前，准确、有效、鲁棒地计算全场测量结果仍然是一个难题，尤其是在大变形或表面不连续的情况下.对于基于图像子区的方法，如何选择图像子区仍然是一个关键问题.一方面，为了可靠地为变形图像的每个图像子区在参考图像中找到最佳匹配，图像子区的大小必须相对较大，使每个图像子区包含足够的强度信息，便于相互区分.而另一方面，由于图像子区中每个点的位移近似表示为一阶或二阶形状函数，图像子区的大小必须相对较小，以尽可能减少近似误差.一个合适的图像子区大小必须足够大又足够小，这是一个两难的问题.如何处理这个问题？

Pan 等人提出了一种选择图像子区大小的方法[30]，利用图像噪声方差和图像子区强度梯度平方和（Sum of Square of Subset Intensity Gradients，SSSIG），通过理论推导预测测量精度，提出了一种在计算位移前选择合适图像子区大小的算法，从11×11 最小图像子区开始逐步扩大，直到SSSIG 刚好大于阈值.Ghulam Mubashar Hassan 等人提出了一种动态图像子区选择（Dynamic Subset Selection，DSS）算法.它使用另一个参数强度变化率在迭代中动态检测最佳的图像子区大小[31].Liang Z 等人提出了一种新的方法来解决选择小图像子区或大图像子区的困境[32]，首先选择一个相对较大的图像子区大小，图像子区中的每个像素都有一个系数，该系数根据像素到图像子区中心的距离计算，然后对相关准则进行了修正，对图像子区中的像素做不同的处理，实际上达到模糊图像子区边界的效果，从而巧妙地避免了确定最佳图像子区大小的问题.

上述选择图像子区大小的方法有一个共同点，即图像子区大小是固定的、统一的.这种方法在试件连续变形时是有效的，但是当试件存在损伤区域（如裂纹时），由于应力集中，在后续变形过程中，损伤区域附近各点的位移可能会发生更为复杂的变化.因此，为了更好地近似表示位移，应该更多地关注图像子区中心附近的点，同时，远离图像子区中心的点也不能完全忽略，因为它们也可能包含有用的匹配信息.

为此，本文提出一种多尺度图像子区匹配算法，利用权重函数调整图像子区内各个像素点对图像子区相关性的贡献，使图像子区的边界完全变得模糊，实现动态调整图像子区大小，更加合适大形变或不连续形变的表面，通过实验证明了该方法能够得到足够精确的测量结果.

1 数字图像相关方法

为了获得全场位移，首先必须能够识别出试件表面的每一点，通常的做法在试件表面喷涂随机散斑图案，使每一个点周围区域互不相同.随着试件的变形，每个区域也发生了变形.然后，选取变形图像中某一点，根据其周围图像子区的灰度信息在参考图像中跟踪对应的点，如图1 所示.

图1 图像子区变形示意图

在一个图像子区中，假设变形是均匀分布的，即点的位移在水平和垂直方向上都是线性变化的，由形状函数进行描述：

对照组-男、女占比各为29:21;年龄范围上限值86岁,下限值62岁,年龄平均值(74.21±1.35)岁。

其中xPQ和yPQ分别是P 点距离其图像子区中心点Q 的水平距离和垂直距离.

由一阶泰勒展开得到

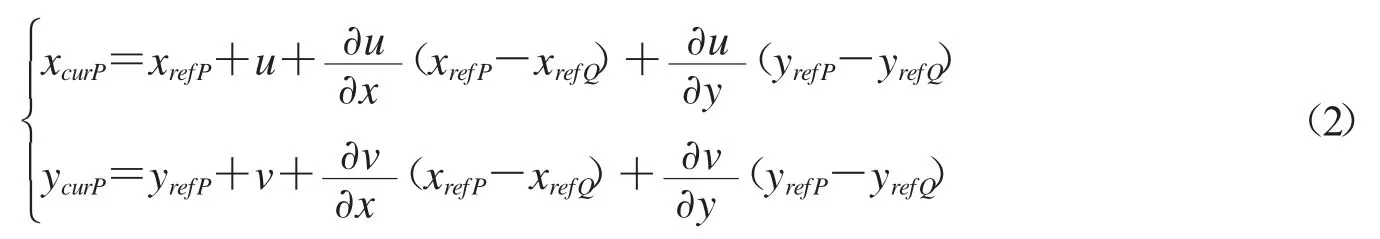
其中，xrefQ和yrefQ表示参考图像中Q 点的坐标.xrefP和yrefP表示参考图像中P 点的坐标.xcurP和ycurP表示变形图像中P 的坐标.u 和v 分别为Q 在x 方向和y 方向的位移.它们的偏导数表示为DIC 分析的目的就是找出

为了评价变形图像子区与参考图像子区之间的相关性，需要一个相关准则.到目前为止，已经报道了许多相关标准，如交叉相关（cross-correlation，CC）、归一化交叉相关（normalized cross-correlation，NCC）、平方和差（sum of squared difference，SSD）等.然后，对每个点应用FA-NR 算法[19]或IC-NG 算法[23]求p→的最优值，使相关系数取得最小值.

2 多尺度图像子区匹配算法

从观测尺度来说，每一个点都是根据其周围的灰度信息来识别的，这些灰度信息通过一个窗口即图像子区来观察.然而，通常很难确定观测窗的大小，因为观测窗必须足够大，才能包含唯一的灰度信息，但又必须足够小，以用形状函数近似表示内部位移分布.这就是在现有方法中难以自动确定最优图像子区大小的根本原因.为此，本文提出在多尺度下重新考虑图像子区大小选择问题.

正如我们所知，多尺度分析在图像处理中已经被广泛应用多年，已经开发出许多分析工具，例如 Curvlet[34]、Wedgelet[35]、Bandelet[36]、Grouplet[37-38]、Beamlet[39-40].多尺度分析的主要思想是将一个信号（图像）分解成多个尺度的分量，通过不同的观测窗口提取出特定的特征.

在DIC 中，为了将变形图像中的一个点与参考图像中的另一个点进行匹配，仅使用图像本身的信息是不够的，因为任何一张图像中都可能有大量相同灰度值的点.因此才必须考虑图像子区中包含的周围信息，根据一定相关准则来区分各个点.

权重函数在评价两个图像子区相似性时确定各个点的重要性，其中Δx 和Δy 表示当前点到图像子区中心点的x 方向距离和y 方向距离.

设f（x，y）表示参考图像，g（x，y）表示测试图像，图像子区的边长为2M+1，以图像子区中心点为坐标原点，则最小平方（Least Square，LS）相关准则[33]定义为：

其中，

将其推广为加权系数：

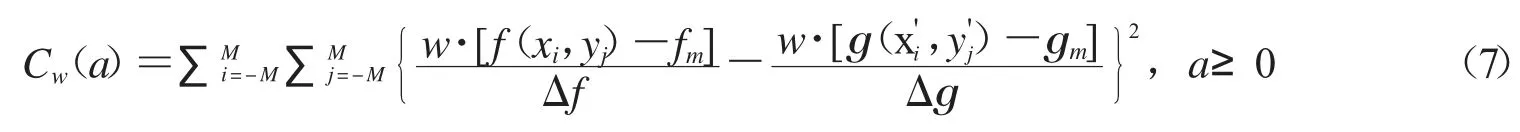
其中

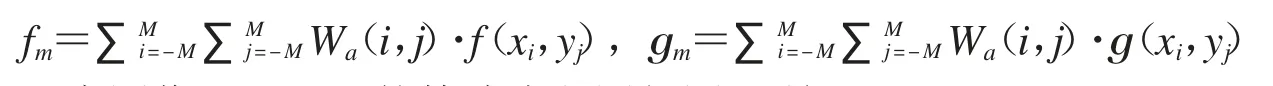
基于多尺度图像子区匹配的算法流程图如图2 所示.

图2 基于多尺度图像子区匹配的算法流程图

对每个要处理的点搜索其最佳尺度因子a.首先设置a 的初始值，计算第一个点时，a 的初始值设置为0，计算其余点时，a 的初始值从前一个已计算的点继承而来的.然后，对当前点进行并行计算，找出最大加权系数Cw（a）并更新接下来，使a 变大或变小，直到使Cw（a）得到最优值，此时，最后更新就是所求结果.

3 实验结果与分析

为了准确评估测量精度，首先采用Matlab 模拟生成数字散斑图像.散斑图像的大小为W×H，散斑密度为ρ，每个散斑具有固定半径R，中心点坐标随机均匀分布，由这N 个散斑叠加形成散斑图像的表达式为：

其中N=W×H×ρ 表示散斑个数，（xn，yn）表示第n 个散斑的中心点坐标.xn和yn分别是均匀分布在[1，W]和[1，H]之间的随机整数.但是，由于数字图像的像素值的取值范围是[0，1]，故对I 必须再做规范化处理：

设置散斑密度ρ=0.05，散斑半径R=1，生成的256×256 数字散斑图像如图3.

图3 模拟生成的数字散斑图像

假设材料泊松比μ=0.2，在计算机上模拟试件受y 方向的平行压力时表面散斑图像的变化，具体地，将位移参数设置为ux=0.02，vy=-0.1，uy=vx=0.

接下来，取图像中心点（128，128）作为种子点，经过IC-NG 算法10 次迭代得到最终的变形向量

表1 模拟DIC 实验中迭代计算过程中的相关性系数 C（）

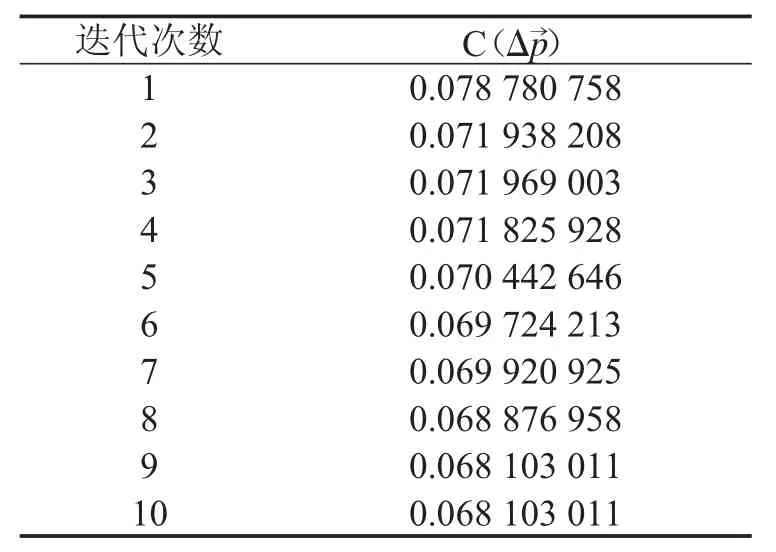
表1 模拟DIC 实验中迭代计算过程中的相关性系数 C（）

迭代次数 C（Δp→）1 0.078 780 758 2 0.071 938 208 3 0.071 969 003 4 0.071 825 928 5 0.070 442 646 6 0.069 724 213 7 0.069 920 925 8 0.068 876 958 9 0.068 103 011 10 0.068 103 011

图4 模拟实验中迭代计算过程中的相关性系数 C（）的变化趋势图

最后得到的计算结果及误差如表2 所示.

表2 模拟DIC 实验的计算结果与误差

表2 同时给出了文献[31]方法和文献[32]方法的计算结果作为对比，可以看出，本文方法的计算精度优于另外两种方法，其中，本文方法的计算结果与文献[32]方法的计算结果更接近，说明像素加权策略对提高计算精度起主要作用，同时由于本文方法吸收了文献[31]方法的动态调整策略，两者结合进一步提高了计算精度.

本文方法计算所有点后可以得到x 方向的位移场u 和y 方向的位移场v，如图5 所示.

图5 模拟DIC 实验的计算结果

为了进一步验证本文方法的性能，在汕头大学材料实验室进行一次真实的DIC 实验，试件是一块混凝土块，利用万能试验机在y 轴方向加压直至破碎.

实验开始前先拍摄一张参考图像，如图6（a）所示，随着压力增加，试件开始变形，左上角区域出现裂纹并逐步扩展，如图6（b）所示，DIC 计算结果得到的x 方向的位移场u和应变场 Exx 分别如图 6（c）和图 6（d）所示.图 6（c）中蓝绿色表示向负方向（左）位移，红黄色表示向正方向（右）位移，可以看出在，在左侧有明显的黄-蓝分界线，说明试件在此处发生了不连续形变，进一步从图6（d）可以看到很明显的应力集中现象（红色区域），对比图6（b）可知此处正是裂纹所在的区域.本文方法的结果很好地反映了试件发生不连续形变时的位移场和应变场.

图6 真实DIC 实验的计算结果

4 结论

针对数字图像相关（DIC）中如何选择图像子区大小的难题，本文提出一种多尺度图像子区匹配算法，从多尺度的角度给出一种解决方案.首先定义权重函数族，用于调整图像子区内各个像素点对图像子区相关性的贡献，通过迭代过程动态调整图像子区中各点权重，使不同位置的图像子区具有不同的观测尺度因子，从而更加合适不均匀形变、大形变或不连续形变的表面.最后通过实验验证本文算法的性能，模拟DIC 实验中测量位移的相对误差为1.6%和2.8%，在材料实验室中进行的真实DIC 实验也验证了本文方法在材料表面发生不连续形变时能够有效监测到位移和应变的变化.