频率选择性衰落信道DS-CDMA无人机中继通信系统航迹规划
刘海涛,顾新宇,方晓钰,李冬霞
中国民航大学 天津市智能信号与图像处理重点实验室,天津 300300
无人机(Unmanned Aerial Vehicle, UAV)中继通信系统是以无人飞行器作为中继平台的远距离无线通信系统。与传统固定中继通信系统相比,UAV中继通信具有通信距离远、部署方便、中继位置灵活可控、系统构建迅捷、效费比高等诸多优点,因此UAV中继通信具有广阔的应用前景[1]。然而中继平台的高速运动也给UAV中继通信带来了一些特殊问题,例如中继信道快速时变、网络拓扑结构快速变化及中继UAV航迹规划等。因此面向UAV中继通信的特殊问题开展关键技术研究具有重要意义。
中继UAV航迹规划的核心问题是在中继UAV的飞行过程中,寻找一条合适的飞行路线,以保障UAV中继链路传输的可靠性,或保障UAV中继通信网络的高连通性。需要澄清UAV中继通信的航迹规划问题与常规UAV航迹规划问题存在较大差异。常规UAV航迹规划需解决的问题是在一定约束条件下(如路径可飞行性、安全性),在飞行的起点与终点之间寻找一条满足一定性能指标的飞行路线,常见性能指标包括路径长度[2]、传感器覆盖率[3]、探测概率[4]等。
在UAV中继通信网络方面,国内外相关研究如下:为提高中继通信网络的吞吐量,文献[5]基于网络传输速率最大化准则提出了一种两步式UAV航迹优化方法;为提升UAV中继移动自组网的网络连通性,文献[6]基于最优加权质心准则提出了一种多UAV飞行控制方法;为了提升无线传感器网络中的UAV采集传感器信息的效率,文献[7]基于UAV信息采集效能最大化准则提出了一种单元分解航迹规划方法。在点对点UAV中继通信方面,相关研究如下:为解决无法通信的节点间的中继节点快速布置问题,文献[8]基于中继链路构建时间最小化准则提出了一种多项式时间UAV中继节点布置方法;文献[9]提出联合发射与接收波束成型的UAV中继传输方法,并基于信噪比最大化准则给出中继UAV的航迹规划方法;为了降低中继UAV的能量消耗,文献[10]基于能量效率最大化准则提出了中继UAV转弯半径的优化方法;针对空时分组编码的UAV中继通信系统,文献[11]基于双跳链路遍历容量最大化准则提出了中继UAV的航迹规划方法。
在以上研究中,UAV中继信道均建模为频率非选择性衰落信道,而在实际系统中,当链路传输速率较高时,UAV中继信道呈现为频率选择性衰落,使中继链路传输的可靠性显著下降,因此需要面向频率选择性衰落信道开展中继UAV航迹规划研究。在频率选择性衰落信道环境下,常见的传输方法有正交频分复用[12]、单载波频率均衡[13]及直序列码分多址(DS-CDMA)[14]。鉴于DS-CDMA传输方法具有保密性高、通过Rake接收可显著改善链路传输可靠性的优势,本研究采用了DS-CDMA的中继传输方法。首先建立了DS-CDMA的UAV中继通信系统模型,随后引入扩频信号模型、频率选择性衰落信道模型和最大比值合并(Maximum Ratio Combining, MRC) Rake接收机模型,分析给出UAV中继通信系统的链路中断概率计算公式,并以链路中断概率最小化准则为基础提出了中继UAV的航迹规划方法,最后仿真验证了所提出方法的正确性与有效性。论文有两个方面的创新:① 提出了基于DS-CDMA的UAV中继通信系统的航迹规划方法;② 理论分析给出了DS-CDMA的UAV中继通信链路平均误码率计算公式。
1 DS-CDMA的UAV中继通信系统模型
1.1 系统模型
图1给出了点对点UAV中继通信系统模型。系统由地面移动用户节点(Mobile User, MU)、固定翼UAV中继节点及地面固定部署的基站节点(Base Station, BS)组成,研究对象为MU到BS上行链路。假设MU与BS节点的距离遥远,不存在两个节点的通信链路,因此必须借助UAV节点的中继才可实现MU节点到BS节点的通信。考虑到两跳链路之间信道均呈现频率选择性衰落,且远距离传输存在路径损耗效应,因此将MU-UAV链路及UAV-BS链路信道建模为包含路径损耗的频率选择性Nakagami-m衰落信道[15-17]。此外为了克服信道的频率选择性衰落,本文采用了DS-CDMA传输方案, UAV节点采用译码转发(Decode and Forward, DF)方式中继信号,且UAV与BS节点的接收机均采用MRC Rake接收方法。在前人的研究中,缺乏频率选择性衰落信道的DS-CDMA的UAV中继通信系统信号模型的完整介绍,以下将构建相应的信号模型。
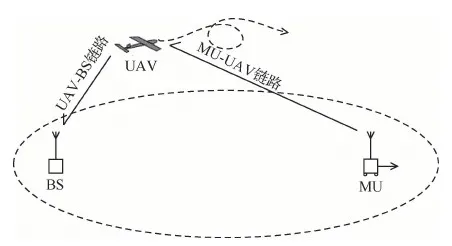
图1 点对点UAV中继通信系统模型Fig.1 Point-to-point UAV relay communication system model
1.2 信号模型
在UAV中继通信过程中,MU节点至BS节点的中继通信过程分为两个时隙。第一个时隙内,MU节点对比特序列进行BPSK调制,随后将调制的码元序列{an}进行扩频调制后发送,则UAV节点接收到的低通等效信号表示为
τi)+zU(t)
(1)
式中:AM为发射信号幅度;N为码元序列长度;Ts为码元周期;q(t)为归一化扩频特征波形;I为MU-UAV信道径数;g(t,τi)为MU-UAV第i径信道衰落系数;τi为MU-UAV第i径信道传输时延;zU(t)为MU-UAV信道复高斯白噪声,其均值为0,方差为N0。
式(1)的接收信号送入图2所示的MRC Rake接收机[18]。根据附录A的推导,得MRC Rake接收机输出的第m个码元检验统计量为
(2)
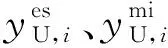
(3)
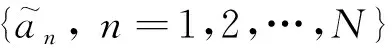
h(t,μj)+zB(t)
(4)
式中:AU为UAV节点发射信号幅度;J为UAV-BS信道径数;h(t,μj)为UAV-BS第j径信道衰落系数;μj为UAV-BS第j径信道传输时延;zB(t)为UAV-BS信道复高斯白噪声,其统计特性与zU(t)相同。
BS节点接收到信号后,同样使用MRC Rake接收方法恢复出UAV节点发送的码元序列,参考附录A的推导,BS节点MRC Rake输出的第m个码元检验统计量表示为
(5)
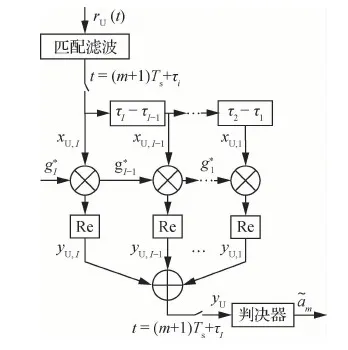
图2 MRC Rake接收机模型(UAV节点)Fig.2 Maximum ratio combining Rake receiver model (UAV node)

(6)
1.3 信道模型
MU-UAV信道为包含路径损耗的频率选择性衰落信道,其第i径衰落系数建模为[15-16]
(7)
式中:u(t,τi)为第i径小尺度衰落系数,其包络服从Nakagami-m分布;dMU为MU到UAV的距离;α为MU-UAV信道路径损耗因子。g(t,τi)的二阶原点矩由如下多径强度分布得到[18-19]
(8)
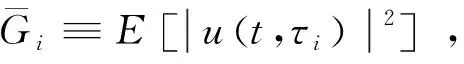
UAV-BS信道同为包含路径损耗的频率选择性衰落信道,其第j径衰落系数建模为
(9)
式中:w(t,μj)为第j径信道小尺度衰落系数,其包络服从Nakagami-m分布;dUB为UAV到BS的距离;β为UAV-BS信道路径损耗因子。h(t,μj)的二阶原点矩由如下多径强度分布得到
(10)
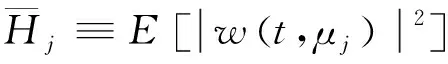
2 UAV中继通信系统的航迹规划方法
链路中断概率是衡量通信链路传输可靠性的重要技术指标,本节基于MU-UAV-BS链路中断概率最小化准则给出一种中继UAV的航迹规划方法。
2.1 MU-UAV-BS链路中断概率
利用文献[20]的研究结果,对于采用DF协议的中继通信系统,当UAV节点输入信干噪比及BS节点输入信干噪比均较高时,MU-UAV-BS链路可等效为单跳链路,且该链路的等效信干噪比为
γeq=min{γU,γB}
(11)
则MU-UAV-BS链路的中断概率可表示为
Pout=P(γeq≤γth)=1-[1-P(γU≤γth)]·
[1-P(γB≤γth)]
(12)
式中:γth为门限值。根据附录B的推导,可得MU-UAV-BS链路中断概率的上界为
Pout,u=1-
(13)
式中:ci和ej分别为u(t,τi)和w(t,μj)的Nakagami-m衰落因子[17];ξi及ζj分别定义为
2.2 基于中断概率最小化准则的航迹规划
假设UAV在中继通信时,UAV飞行状态平稳,飞行高度固定为C、飞行速度固定为vU,UAV仅通过改变航向角来优化飞行航迹。假设UAV航向角的更新周期为T,且在(l-1)T时刻UAV的坐标为(XU,l-1,YU,l-1,C),根据Dubins运动模型[9]可得lT时刻UAV的坐标为
(14)
式中:δl=δl-1+Δδl为lT时刻UAV的航向角,其中Δδl为lT时刻UAV的转弯角,且Δδl∈ [-Δδmax,+Δδmax], Δδmax为UAV最大转弯角。

图3 δl、δl+1和Δδl+1的关系Fig.3 Relationship betweenδl, δl+1 and Δδl+1
图3描述了参量δl、δl+1及Δδl+1的关系。图中,Pl-1、Pl及Pl+1分别为UAV在(l-1)T、lT及(l+1)T时刻的位置;vl为UAV在lT时刻的速度矢量。由图3可知,UAV飞行至Pl点处时,Δδl+1为lT~(l+1)T内的转弯角,则UAV的航向角由δl变化为δl+1,即δl+1=δl+Δδl+1。
假设BS节点坐标为(XB,YB, 0),且lT时刻MU节点坐标为(XM,l,YM,l,0),则lT时刻UAV节点至MU及BS节点的距离分别为
(15)
dUB=[(XB-XU,l-1-vUTcosδl)2+
(16)
进一步将式(15)与式(16)代入式(13),可得lT时刻UAV中继通信系统的链路中断概率的上界为
Pout,u=1-[1-F(c1,c2,…,cI;θ1,θ2,…,θI)]·
[1-F(e1,e2,…,eJ;φ1,φ2,…,φJ)]
(17)
式中:
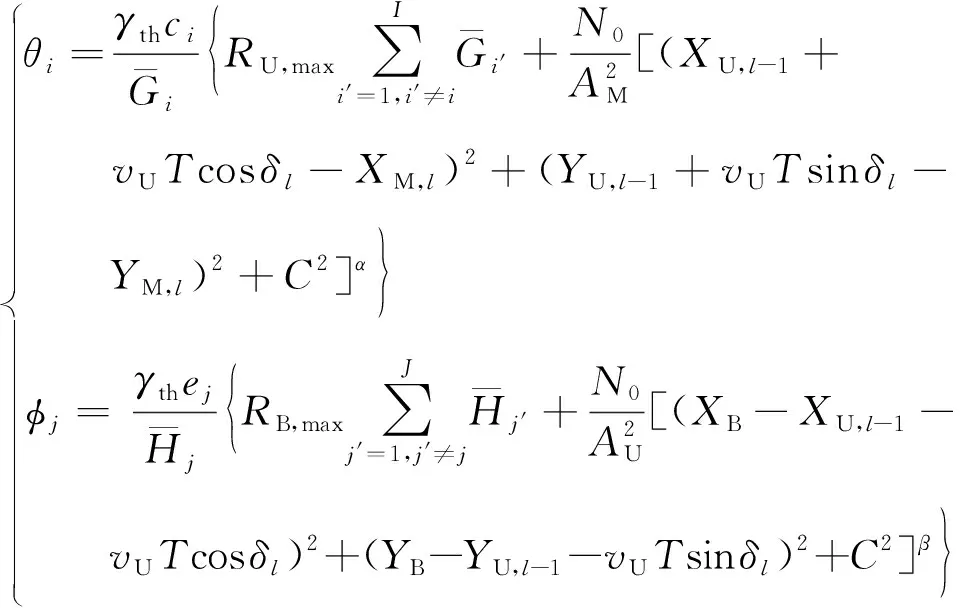
式(17)表明:在(l-1)T时刻UAV位置给定的情况下,lT时刻UAV中继通信系统的链路中断概率仅取决于lT时刻UAV的航向角δl。因此可通过优化UAV的航向角δl来使lT时刻链路中断概率最小化。UAV航迹规划问题可表示为
s.t.δl-1-Δδmax≤δl≤δl-1+Δδmax
(18)
式(18)给出的数学问题是一个带约束条件的一维非线性优化问题,由于代价函数表达式较复杂,通常情况可采取一维搜索方法得到最优解。
3 MU-UAV-BS链路平均误码率
根据附录C的推导,可得MU-UAV-BS链路的平均误码率为
(19)
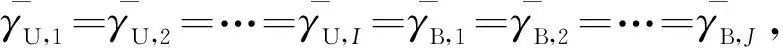
4 系统仿真
为验证所提出UAV航迹规划方法的正确性与有效性,本节构建了DS-CDMA的UAV中继通信仿真系统,给出了UAV二维平面航迹图,并仿真给出了系统性能。
4.1 仿真条件
仿真系统的主要技术参数如下:仿真时长为1 000 s;处理增益K=511;伪随机序列采用511位的m序列;中断概率截短项数R=10。MU码元幅度AM=10 V;起始位置(10,0) km,高度恒为0 m,速度vM=20 m/s,且按照确定轨迹运动。MU-UAV链路信道径数I=3;附加时延τ2-τ1=Tc,τ3-τ2=5Tc;指数衰落因子ε=0.5/Tc。UAV节点的接收机噪声功率谱密度N0=-122 dBW/Hz,码元幅度AU=10 V,用于计算中断概率的门限值γth=0 dB;初始位置为(0,0) km,飞行高度恒为1 km,速度vR=40 m/s,最大转弯角δmax=3°。UAV-BS链路信道径数J=3,附加时延μ2-μ1=Tc,μ3-μ2=5Tc,指数衰落因子κ=0.5/Tc。BS节点的噪声功率谱密度同N0,门限值同γth;坐标恒为(0,10) km,高度为0 km。
仿真实验分为如下3种场景:场景1,MU-UAV及UAV-BS信道的路径损耗因子相同,α=β=1.7[15],UAV及BS节点均采用MRC接收方法;场景2,MU-UAV及UAV-BS信道路径损耗因子与场景1完全相同,但UAV及BS节点采用选择合并接收方法[17];场景3,MU-UAV信道的路径损耗因子α=1.7,UAV-BS信道的路径损耗因子β=1.8,UAV及BS节点的接收方法与场景1完全相同。
4.2 仿真结果
图4给出了场景1环境下UAV的飞行航迹。其中,黑色曲线表示MU节点运动轨迹;蓝色曲线表示UAV航迹。曲线比较表明:① 所提出的航迹规划方法能够引导UAV节点跟踪MU节点的运动,并使得UAV节点位于BS及MU节点间飞行;② 由于UAV节点飞行速度大于MU节点的移动速度,在某些时刻UAV节点通过绕圆形飞行方式跟踪MU节点的移动,以保障链路传输性能最优。
图5给出了链路中断概率和误码率随时间变化曲线(场景1)。其中,蓝色曲线为理论性能曲线;符号“○”表示相应时刻的仿真性能。曲线比较表明:链路中断概率及误码率仿真性能曲线与理论计算结果完全一致,验证了理论计算公式的正确性。
图6给出了不同仿真场景下UAV的飞行航迹(场景1+场景2+场景3)。其中,黑色曲线表示MU节点运动轨迹;蓝色曲线表示场景1的UAV航迹;红色“—·”曲线表示场景2的UAV航迹;绿色虚线表示场景3的UAV航迹。由图6可观测到以下结果:①场景1与场景2的UAV航迹基本保持一致,这表明UAV及BS节点的接收方法对UAV航迹影响不明显;②比较场景1与场景3的UAV航迹,可知:当UAV-BS信道路径损耗因子大于MU-UAV信道路径损耗因子时,UAV航迹明显偏向BS节点,这表明信道路径损耗因子对UAV航迹影响更明显。
图7给出了不同场景下链路中断概率及误码率随仿真时间变化的曲线(场景1+场景2)。其中,蓝色曲线及标识“○”分别表示场景1的理论曲线及仿真曲线;红色曲线及标识“□”分别表示场景2的理论曲线及仿真曲线。曲线比较表明:尽管场景1与场景2的UAV航迹基本一致,但场景1的链路中断概率及误码率性能明显优于场景2。这表明:MRC接收方法可充分获取频率选择性衰落信道提供的分集增益,显著改善链路传输可靠性。
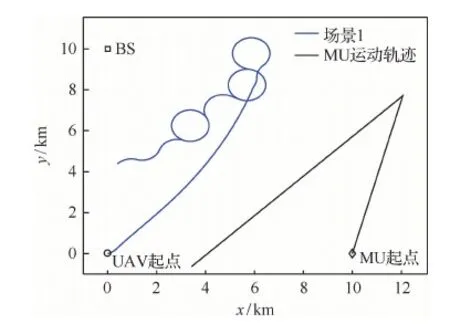
图4 中继UAV的飞行航迹(场景1)Fig.4 Trajectory of relaying UAV (Scenario 1)
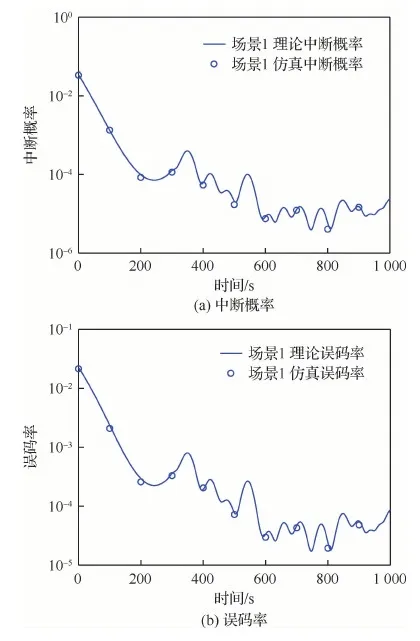
图5 链路性能随仿真时间变化的曲线(场景1)Fig.5 Variation of link performance with simulation time (Scenario 1)

图6 中继UAV的飞行航迹(场景1,场景2,场景3)Fig.6 Trajectory of relaying UAV (Scenario 1, Scenario 2,Scenario 3)
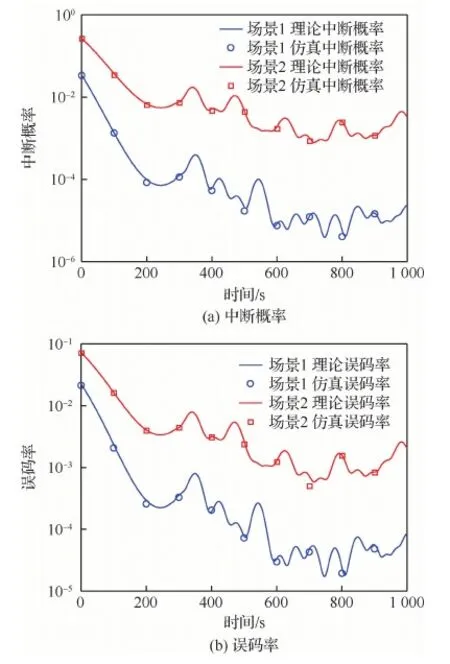
图7 链路性能随仿真时间变化的曲线(场景1+场景2)Fig.7 Variationof link performance with simulation time (Scenario 1+Scenario 2)
5 结 论
针对频率选择性衰落信道中继UAV的航迹规划问题,基于链路中断概率最小化准则提出了DS-CDMA的UAV中继通信系统的航迹规划方法。本文研究结论如下:
1) 所提出航迹规划方法可引导UAV中继节点跟踪移动用户节点的运动,使UAV中继节点处于最佳中继位置,以保障链路传输的可靠性。
2) 采用MRC接收机的DS-CDMA的UAV中继通信系统可充分获取频率选择性衰落信道提供的分集增益,显著改善链路传输可靠性。
附录A MRC Rake接收机输出信号推导
不失一般性,以下以第m个码元的接收为例求得UAV节点MRC Rake输出信号。为了分离出接收信号rU(t)中的第i路有用信号,剥离其余I-1路干扰信号,需要对接收信号进行匹配滤波。假设接收端通过对[mTs+τi,(m+1)Ts+τi]内的信号进行匹配滤波来获得第i路第m个码元信号,特征波形q(t)对应的匹配滤波器为q(Ts-t)[21],码元最佳抽样时刻为(m+1)Ts+τi,并记gi=g(mTs,τi),则接收信号匹配滤波输出为
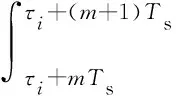
(A1)
式(A1)可进一步化简为
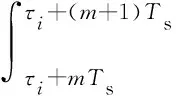
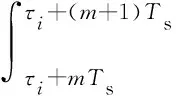
(A2)
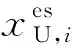
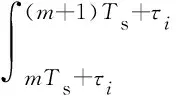
q(τ-mTs-τi)dτ
假设信道衰落系数在单个码元传输期间内恒定不变,且接收机已经获取精确的信道估计值,则MRC输出的第m个码元检验统计量表示为
(A3)
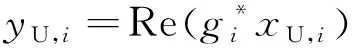
MRC输出信号送入判决器进行判决,相应的判决准则表示为
(A4)
附录B MU-UAV-BS链路中断概率推导
由于精确计算P(γU≤γth)非常困难,论文首先给出UAV节点MRC输出信号yU的信干噪比的一个下界,并进一步得到P(γU≤γth)的上界。
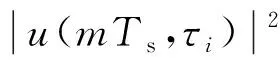
(B1)
进一步得到MRC输出信干噪比为
(B2)
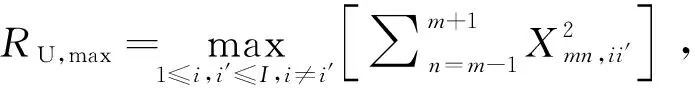
(B3)
由式(B3)可得P(γU≤γth)的上界为
(B4)
利用文献[22]的结果,P(γU≤γth)的上界表示为
(B5)
式中:F(c1,c2,…,cI;z1,z2,…,zI)定义为
F(c1,c2,…,cI;z1,z2,…,zI)=
(B6)
式中:(a)b=Γ(a+b)/Γ(a)为Pochhammer符号,Γ(·)为Gamma函数。
针对UAV-BS链路,使用相同的分析方法,可得BS节点MRC输出的信干噪比的下界为
(B7)
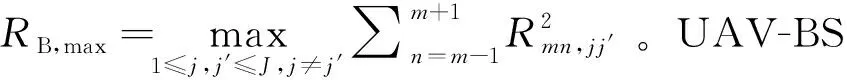
P(γB≤γth)≤
(B8)
最后,将式(B5)和式(B8)代入式(12),并令f1≤R,f2≤R,…,fmax{I,J}≤R,即可得MU-UAV-BS链路中断概率的上界。
附录C MU-UAV-BS链路平均误码率推导
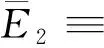
P{E3|γB})+P{E3|γB}(1-P{E2|γU})
(C1)
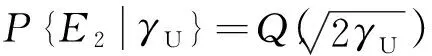
(C2)
最后,对式(C2)中的γU和γB进行统计平均,可得MU-UAV-BS链路的平均误码率为
P(E2)+P(E3)-2P(E2)P(E3)
(C3)
式中:fU(x)和fB(y)代表输入信干噪比γU和γB的概率密度函数;参考文献[22]的研究,P(E2)和P(E3)的表达式分别为
(C4)
(C5)
式中:φU,i=ci/(ci+E[γU,i]);φB,j=ej/(ej+E[γB,j])。将式(C4)及式(C5)代入式(C3),即可得平均误码率表达式。
附录D 系统分集增益推导
根据第4节的信道对称假设,可将式(C4)与式(C5)近似表示为
(D1)
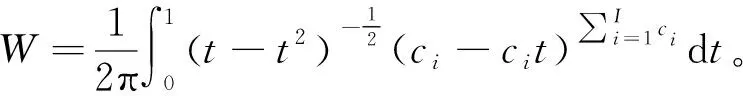
(D2)