CFRP反射器型面主动控制和作动器位置优化

伍科，张华振，兰澜,周阳

1. 西安空间无线电技术研究所，西安 710100 2. 上海跃盛信息技术有限公司，上海 200240

高精度、大空间反射器的研究越来越受到人们的关注。提高反射面精度的方法是人们对高精度反射器研究的重要方向。国外已有了许多高精度反射器研究的方法和案例。

Pearson等[1]研究了一种大型高精度充气薄膜反射器的设计和分析方法。Lang等[2]设计了一种高精度壳体反射器结构，并提出了一种壳体反射器的结构优化和型面调整方法。Shi等[3]提出了一种对于空间索网反射器网面的几何生成方法。Yuan等[4]提出了一种可提高大型可展开网格反射器表面精度的设计方案。Soykasap和Tan[5]设计并分析了一种高精度采用偏置加筋弹簧支撑的碳纤维增强复合材料(CFRP)反射器。虽然被动的方法对提高反射面精度做出了很大努力,但主动型面控制方法仍是提高反射面精度的最有效途径之一。

智能材料和结构,诸如聚偏氟乙烯(PVDF)、锆钛酸铅(PZT)、宏观压电纤维复合材料(MFC)、形状记忆合金(SMA) 作动器/传感器广泛应用于主动型面/振动控制。Tabata和Natori[6]研究了空间可展开天线的反射器主动型面校正方法以及其可行性。Fang等[7]提出了一种运用PVDF作动器对大型高精度薄膜反射器进行自适应控制的系统设计方案。Wang等[8]提出了一种求解压电作动器控制电压的方法，并将其用于空间反射器的型面调整。Stein和Gorinevsky[9]开发了一种利用大型封装PZT作动器阵列对反射面进行主动形状控制的技术。Andoh等[10]提出了一种利用有限个数的作动器对反射器型面进行控制的方法。Lu等[11]采用SMA作动器,来提高圆形薄膜结构的型面精度，建立了薄膜结构的分析模型和求解方法，并利用有限元方法验证了典型热载荷下分析模型的有效性。Desmidt等[12]研究了一种主动绳索控制系统及其可行性,并将其应用于控制由热载荷引起的反射器型面的全局误差。Wu等[13]提出了利用PZT和MFC作动器同时进行主动控制，分别用来降低CFRP格栅反射器的全局型面误差和局部型面误差。宋祥帅等[14]运用影响系数矩阵法研究了格栅反射器的作动器电压配置问题，得到了使型面均方根误差最小的电压值和相应的均方根(RMS)误差，但对于作动器数量的限制和位置的优化配置问题并没有进行研究。

大型空间反射器结构由于在发射过程中受结构重量和体积的限制而无法使用过多数量的作动器。因此，为了提高反射器结构型面主动控制效率，研究在有限数量作动器的条件下，作动器位置优化分布至关重要。

目前已经有较多的研究针对振动或者型面控制中作动器的几何尺寸、空间分布位置和加载电压进行了优化。但大多数研究集中于研究梁、板结构的振动和形状控制。

Suleman和Goncalves[15]优化了矩形悬臂组合梁的驱动器的尺寸和位置,其目标是使结构的位移最大、质量和电压最小。Adali等[16]采用一维搜索的优化算法来确定层合梁结构的作动器位置。Aldraihem等[17]优化了执行器的长度和位置,其目标函数是使进行加权后可控性最大。Barboni等[18]通过最优性条件的解析解，优化了振动控制中简支梁执行器的长度和位置。Bruant等[19]采用基于梯度的优化方法对3根梁组合结构中作动器的长度和位置进行了优化，其目标为使机械能最小以及系统的可观测性最大。

以上这些方法的共同特点为优化迭代的前进方向基于目标函数对优化变量的梯度。其优点为对于凸规划问题能够精确地逼近目标函数的最优解。但是，对于复杂的大型空间结构或大型离散变量的优化问题，精确获取目标函数的梯度十分困难，且基于梯度的优化方法容易陷入局部最优解。

随机搜索算法是研究结构振动或者形状控制问题中的另一种优化方法。Dong和Huang[20]研究了基于多点近似函数和遗传算法(GA) 的桁架拓扑优化问题。An等[21]采用两级多点逼近法研究了自适应桁架的作动器分布的优化问题。Liu和Lin[22]通过模拟退火算法对于悬臂板的形状控制问题优化了作动器分布和相应控制电压。

随机搜索算法的优点在于不需要获得目标函数的梯度,对于复杂优化问题和离散变量的优化问题具有明显的优势。但随机搜索算法所得到的最优解的精度可能低于基于梯度的方法。

本文研究了基于PZT作动器的CFRP主控格栅反射器的型面控制问题。首先，采用了一种具有独立电压自由度的梁单元，以及考虑高阶剪切变形的板单元，并运用能量变分哈密尔顿原理推导出了主控格栅反射器的有限元控制方程，根据推导的有限元控制方程，给出了反射面型面残余RMS误差最小的电压最优控制方法。

对于型面控制中的作动器位置优化分布问题，基于控制后残余RMS误差最小，提出了一种将自适应遗传算法和梯度投影方法相结合的改进优化方法，以解决在限定作动器数量的条件下，作动器几何位置的优化问题。这种方法采用遗传算法获得作动器的几何分布，采用罚函数法约束作动器的个数，然后运用梯度投影方法求解约束二次规划问题中作动器的电压。通过数值算例得到并验证了提出算法的正确性和有效性。制作了大型主控格栅反射器的实验样机，在高精度光学平台上针对CFRP格栅反射器的制造误差运用PZT作动器进行了型面控制实验。

1 有限元模型

主控CFRP格栅反射器的几何模型如图1所示。反射器所使用的CFRP材料铺层方向为[0°/45°/-45°/90°]s。PZT作动器的总数为72个，通过预紧螺母安装在每一个小格栅的开凿处。反射器约束的位置为格栅中心交叉处，约束方式为锁定中心处6个自由度的位移。格栅反射器的设计几何尺寸如表1所示。

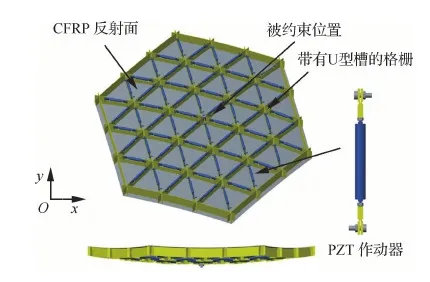
图1 主控CFRP格栅反射器的几何模型Fig.1 Geometric schematic of active CFRP rib reflector

表1 主控格栅反射器的结构参数Table 1 Structural parameters of active rib reflector

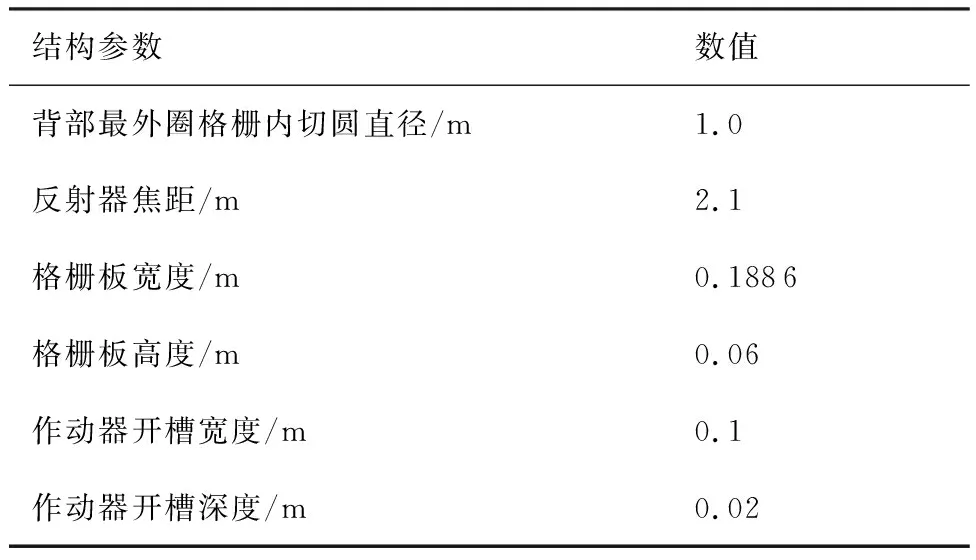
结构参数数值背部最外圈格栅内切圆直径/m1.0 反射器焦距/m2.1 格栅板宽度/m0.1886 格栅板高度/m0.06 作动器开槽宽度/m0.1 作动器开槽深度/m0.02

1.1 位移和应变假设

Reddy[23]提出了一种考虑高阶剪切形变的层合板单元，它相比普通层合板单元具有更高的计算精度。本文使用这种考虑高阶剪切变形的层合板单元来对CFRP层合板进行建模。假设其位移可以写为

u(x,y,z)=u(x,y,0)+zφy(x,y,0)-

(1)

v(x,y,z)=v(x,y,0)+zφx(x,y,0)-

(2)

w(x,y,z)=w(x,y,0)=w0(x,y)

(3)

式中：u、v、w为板单元沿x、y、z方向的位移；φx和φy分别为在yOz和xOz平面内的转角；h为层合板的厚度。坐标系为定义在板单元几何中心处的单元局部坐标系，平面z=0为层合板厚度方向中心面所在的平面，层合板的几何方程为

(4)

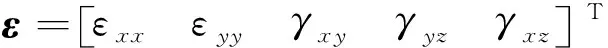
对于PZT作动器，运用三维梁单元对其进行建模，假设其位移可以写为

u′=u′0(x,0,0)+yφ′z(x,0,0)+zφ′y(x,0,0)

(5)

v′=v′0(x,0,0)

(6)

w′=w′0(x,0,0)

(7)

式中:u′、v′和w′为PZT梁单元沿x、y以及z方向的位移；φ′y和φ′z分别为在xOz和xOy平面内的转角。其坐标系为位移梁单元节点处的单元局部坐标系。三维梁单元的几何方程可以表示为

(8)

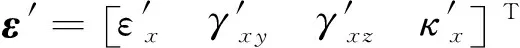
1.2 本构方程

正交各向异性板单元的本构方程为[23]

(9)

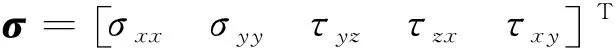
(10)

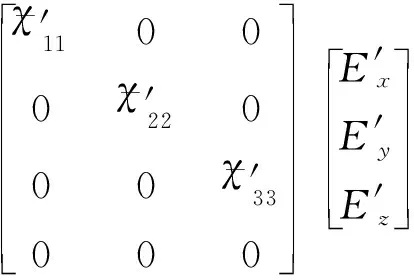
(11)

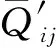
1.3 插值形式

使用4节点的二维板单元对碳纤维层合板进行建模，板单元的每个节点具有7个自由度。运用Hermite插值函数[24]对单元内部区域进行插值。对于板单元,其单元位移向量可以表示为

(12)

单元的节点位移向量de可表示为

(13)

i=1,2,3,4

(14)

式(12)～式(14)中:N为3×28的运用Hermite函数进行插值的板单元型函数矩阵，其具体形式见附录;节点位移向量de为28×1的行向量。将式(12)代入式(4)，板单元的应变向量可表示为

(15)

式中:B为板单元的应变矩阵。

对于PZT压电梁单元，其位移插值形式可以表示为

(16)

应变向量可以表示为

(17)

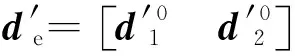
(18)

梁单元的型函数N′的形式见附录A[25]。

1.4 变分形式

运用广义Hamilton变分原理来推导主控系统的平衡方程。广义Hamilton变分等式可以表示为

(19)

式中:K为系统的动能;P为系统的势能;W为外力功;t1和t2分别为起始和终止时间。对于静力学分析，K=0。对于本文研究的主控格栅反射器，其势能包括弹性势能和电势能，其一般形式为

(20)

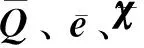
对于PZT压电梁单元，其电场可表示为

(21)

式中:U′e为压电梁单元的加载电压;l为作动器的长度;L为线性算子。将式(16)和式(21)代入式(20)，压电梁单元的总势能进一步可表示为

(22)

(23)

(24)

(25)

式中:K′m、K′me和K′ee分别为力学刚度矩阵、机电耦合矩阵以及电势矩阵。

对于CFRP层合板单元，压电常数矩阵和介电常数矩阵均为零矩阵，单元的势能可以表示为

(26)

式中:Km为CFRP层合板单元的单元刚度矩阵。系统的外力功可以表示为

(27)

(28)

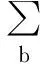
将每个单元中局部坐标系通过乘以相应的雅可比矩阵转换为整体坐标系，在整体坐标系下，对单元节点平衡方程进行组装可以得到在整体坐标系下所有节点平衡方程的矩阵形式。由于变分量的任意性，变分方程式(28)可以转化为整体坐标系下的代数方程：

(29)

式中：d为全局坐标系下的单元节点位移向量；Km、Kme和Kee分别为全局坐标下总力学刚度矩阵、总机电耦合矩阵以及总电势矩阵；U为所有压电单元的电压向量；F为节点的外力向量；Q为作用在压电单元上的外电荷。通过解式(29)，可以得到系统的节点位移和作动器的电压。

2 最优控制器设计

对于研究的主控格栅反射器，本节基于所建立的有限元模型，设计了反射器型面控制的最优控制器。对于反射器在空间环境下所承受的任意力和位移载荷，当作动器数量给定时，均能给出当前数量作动器的最优位置分布以及相应的加载电压，使得控制后残余RMS误差最小。

2.1 型面最优控制数学模型

反射面的几何示意图如图2所示，整体坐标系的原点位于抛物面反射器的顶点。y坐标轴通过抛物面的焦点，反射面上节点的RMS误差被定义为

(30)

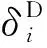
PZT作动器的安装位置为反射器小三角格栅的开凿处，预留的待选位置总共有72个，考虑到作动器的重量，实际使用的作动器个数应少于72。在优化模型中，为了表示一定数量的作动器的分布情况，用一个72位的二进制0，1编码的向量代表该处有没有作动器，1代表该处装有作动器，0代表该处无作动器。因此，根据所建立的主控反射器系统的有限元模型(式(29))，主控反射器型面最优控制的数学模型可以写为

图2 反射器的实际型面和理想型面Fig.2 Actual and desired shapes of reflector

(31)

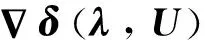
2.2 求解方法

改进的优化方法的具体步骤为

步骤1 由遗传算法随机生成一定数量的二进制向量λ个体作为初始种群，表示作动器分布。

步骤2 对于种群每一个个体，λ为已知二进制向量，交由梯度投影方法求出每一个个体的加载电压以及相应的残余RMS误差，将残余RMS误差作为个体的适应度。

步骤3 保留最优个体，直接到下一代中，不参与交叉和变异。

步骤4 根据个体适应度，通过轮盘赌进行选择，将所选个体运用自适应交叉和变异算子进行筛选并重新插入种群中。

步骤5 更新每一个个体的二进制编码λ，返回步骤2进行迭代，直至种群最优个体适应度变化小于设定值或达到最大迭代次数。

步骤6 输出迭代结束时，种群中的最优个体对应的二进制编码λ，代表作动器的位置分布；相应的电压向量U和相应的残余RMS误差值。

对于步骤2中，当λ确定时，相应电压后残余RMS误差的求解方法为：假设系统的节点总位移个数为p，反射面上节点在y方向的位移个数为q，总电压自由度个数为r。将式(31)中目标函数f写为

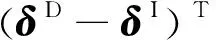
(32)

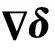
(33)

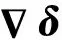
(34)

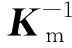
Ks(F-KmeU)(δD-δI)+

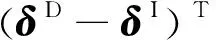
(35)

式(35)可以进一步简化为

f(U)=UTAU-bTU+c

(36)

式中:

(37)

(38)

(39)

A为r×r维的正定方阵;b为r维的列向量;c为常数。同样，优化模型中第3个约束不等式也可以写成矩阵形式。因此，优化模型式(31)可以转化为如下有边界约束的二次规划的形式：

(40)

优化模型式(40)可以通过约束二次规划问题中梯度投影法(GPM)进行求解。

将求得的目标函数即RMS误差作为对应个体的适应度，继续进行步骤3中的选择、交叉和变异，当迭代完成时，即可求出相应载荷下，一定数量作动器的最优位置分布、相应电压以及残余RMS误差。特别地,为了防止在步骤4中，种群中个体在交叉和变异过程中，代表作动器位置的编码向量λ中作动器个数超出限定个数，采用罚函数对作动器超出规定个数的个体对应的目标函数进行惩罚。作动器数量超出的个数越多，罚函数惩罚的力度越大。动态罚函数的表达式为[26]

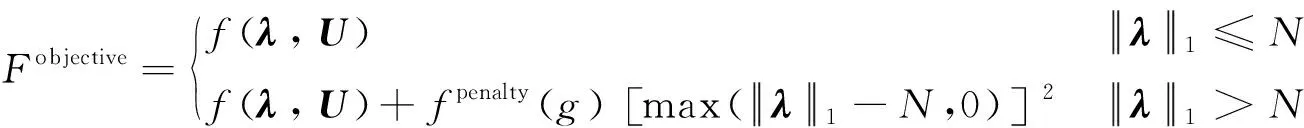
(41)

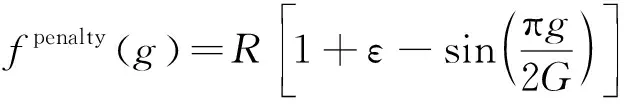
(42)

式中：fpenalty(g)为随种群迭代次数变化的动态惩罚因子;R为反函数比例系数;ε为正的参数;g和G分别为当前的迭代次数和总共的迭代次数。在迭代过程中，产生的新个体作动器数量超过规定数量越多，惩罚的力度越大；并且开始迭代时采用较大的处罚因子，随着迭代次数的增加，逐渐减小，用以提高种群的迭代效率，加速收敛的过程。遗传算法中的交叉、变异算子采用自适应交叉和变异。自适应交叉和变异算子的表达式为

(43)

(44)

式中:Pc1、Pc2为最小以及最大的交叉概率;Pm1、Pm2为最小以及最大的变异概率；f′为种群中个体的适应度；f′max为种群每代个体迭代最大适应度;f′ave为种群每代的平均适应度。

图3为对作动器位置进行优化运用的优化算法流程图。首先随机生成72个代表作动器位置的随机二进制串，作为优化变量；根据每一个二进制变量代表的作动器位置分别建立有限元模型；然后，运用上述方法将型面最优问题转化为式(40) 所述的二次规划问题，求出相应作动器分布情况下对应的电压和残余RMS误差，并将RMS误差作为其种群中个体的目标函数值；根据每一串二进制变量代表的作动器个数是否超出准许范围，运用式(41)和式(42)进行惩罚，从而得到种群中每一个个体的适应度；根据个体的适应度进行选择、交叉和变异操作，从而进化出新的种群，重新进行迭代。保留每一代种群中的最优个体，直到满足结束迭代的条件，将最优个体二进制变量作为作动器分布方式，并求出相应的作动器电压。

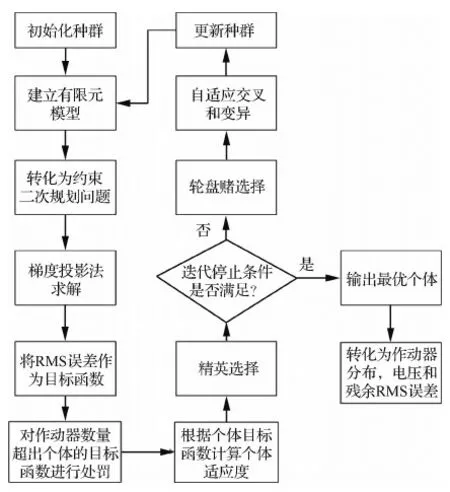
图3 作动器分布位置优化流程Fig.3 Flow chart of actuator placement optimization

2.3 数值算例

式(29)中刚度矩阵可借助于有限元软件ANSYS 14.0进行建立并提取。优化以及控制算法采用MATLAB 2013b进行编制，迭代的过程在MATLAB中进行，完成时给出相应的作动器分布、配置电压以及残余RMS误差。以下给出了两组算例。反射器的约束位置为如图1所示的节点处，其6个自由度被约束。

1) 反射器受整体弯矩作用

施力方式为反射器边缘对称角点处等大反向的10 N垂向作用力，作用点距离为1.1 m，产生的整体弯矩为11 N·m。反射面的初始RMS值为266.5 μm，其位移误差云图如图4所示。

运用本文提出的优化方法，对此工况下作动器的位置分布以及相应电压进行优化。假设N=14,即作动器数量限制为14个。遗传算法的迭代曲线如图5所示。图6为优化后的作动器位置和相应电压大小。

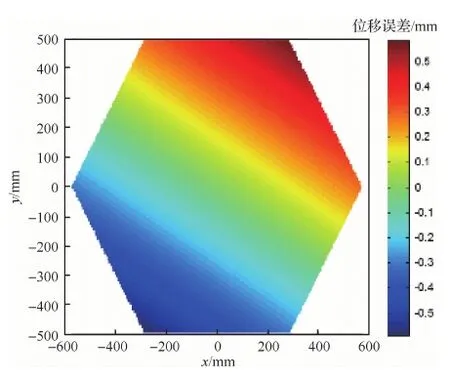
图4 反射面受弯矩作用位移误差云图Fig.4 Contour of displacement error of reflector surface under a bending moment

由迭代曲线图5可以看出，所提出混合优化算法收敛速度很快，80次迭代以后目标值保持不变。控制后的残余RMS误差为44.1 μm。

2) 反射面上节点位移取Zernike多项式线性组合的形式

取六边形域内前5阶正交Zernike多项式组成的线性组合，作为反射面型面节点的位移误差，其表达式为[27]

(45)

式中:Sd(ρ、θ)为反射面上坐标为(ρ、θ)点的位移；Zi(ρ、θ)为第i阶Zernike多项式。将反射面上节点的坐标代入式(45)，可以得到反射面上所有节点的位移误差云图，如图7所示。运用改进优化算法对其进行优化，作动器数量的限制分别设为10、20以及35。图8为3种作动器数量限制时遗传算法的迭代曲线。当作动器数量限制为10个时，残余RMS误差为7.25 μm；当作动器数量限制为20个时，残余RMS误差为5.1 μm；当作动器数量限制为35个时，残余RMS误差为4.9 μm。相应的作动器位置分布情况、电压大小以及残余型面误差云图如图9所示。在当前型面误差情况下，当作动器数量限制从4个一直到72个变化时，将每次优化的最终RMS误差用曲线连接，如图10所示。从图10可以看出，随着作动器数量增加，残余误差逐渐减小，当作动器数量达到临界点(40个)时，控制误差到达最小饱和值。

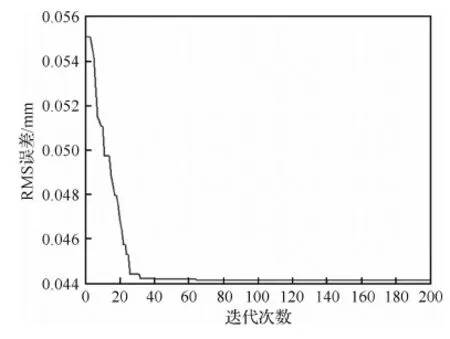
图5 优化迭代曲线(14个作动器)Fig.5 Iteration curve of optimization (14 actuators)

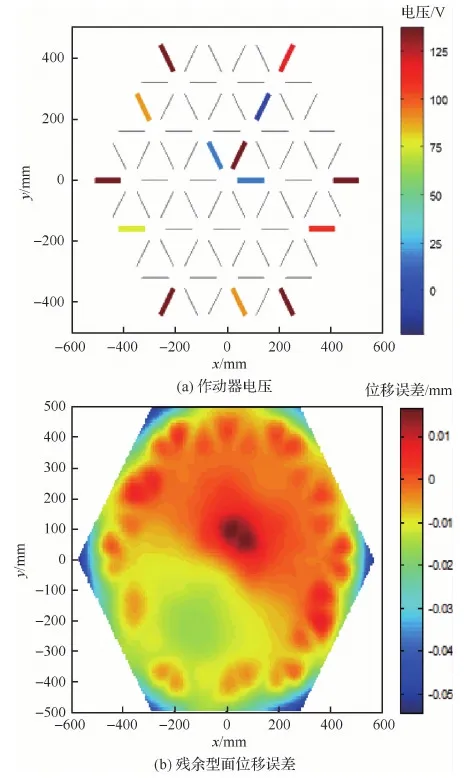
图6 作动器电压以及残余型面位移误差Fig.6 Voltages of actuators and residual surface displacement error

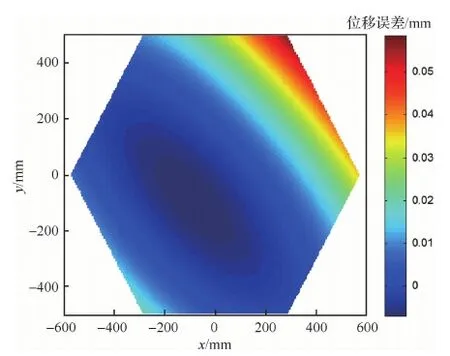
图7 Zernike多项式线性组合的位移误差云图Fig.7 Contour of displacement error of linear combination of Zernike polynomials

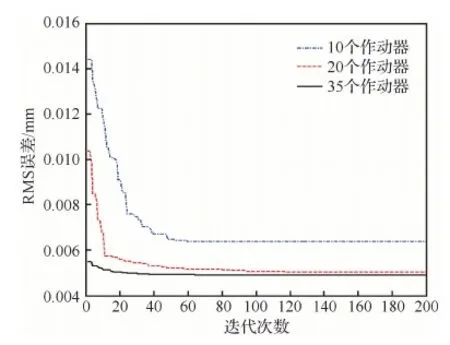
图8 作动器数量分别为10、20和35时的迭代曲线Fig.8 Iteration curves with 10, 20, and 35 actuators

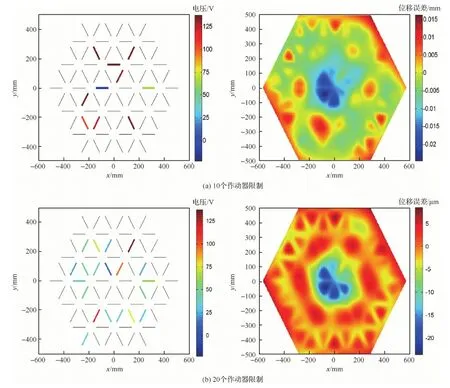
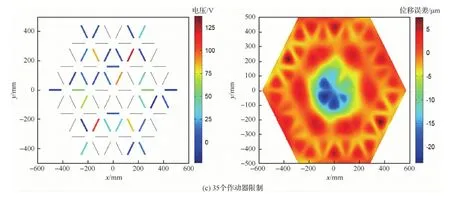
图9 3种情况下作动器电压以及相应残余误差云图Fig.9 Voltages of actuators and corresponding residual surface errors contours in three cases

图10 残余RMS误差随作动器数量的变化Fig.10 Variation of residual RMS error with number of actuators

3 样机制作与实验验证

制作了CFRP复合材料格栅反射器，外沿直径为1.2 m，有效区域为内切圆直径1.0 m的正六边形区域，焦距为2.1 m。格栅反射器的型面主动控制实验系统在恒温恒湿实验室中的高精度光学平台上搭建并完成。实验环境以及主控高精度格栅反射器样机照片如图11所示。每节格栅上安装一个PZT作动器以实现反射器的型面控制，PZT作动器的总数为72支。反射器背部格栅中心处用夹具进行固定并将夹具底座完全固定于光学平台上。图12为作动器电压控制器软件和硬件设施。

反射面上靶点的位移采用V-STARS摄影测量仪进行测量，作为输入电压的反馈。V-STARS摄影测量系统组件如图13所示。它是一种利用光学三角定位法进行标定的高精度摄影测量工具。主控反射器系统实验测量现场如图14所示。

测量靶点共469个，位于反射面上均匀分布。对测量得到的靶点坐标进行定焦拟合，可得到固定焦距下反射面的型面误差。

图11 实验环境和主控格栅反射器样机Fig.11 Experimental environment and prototype of active rib reflector

图12 电压控制系统软、硬件Fig.12 Hardware and software of voltage control system

图13 V-STARS摄影测量系统组件Fig.13 Components of V-STARS photogrammetry system

图14 主动型面控制实验测量系统Fig.14 Experiment measurement system for active shape control

3.1 单个PZT作动器线性度验证

首先对PZT作动器给定电压输入时，反射面产生位移的线性度进行验证，确保分析和实验基本假设的正确性。对反射器上某一内圈作动器分别加载25、50、75、100、150 V电压，并测量反射面上节点相应的位移。5个靶点分别位于图14中反射器边缘的沿双向箭头方向上，标号分别为 1～5。图15为反射面上5个节点在不同电压下的位移曲线，从图可以看出，反射面上节点的位移和电压呈近线性关系，从而从实验上验证了主动控制反射器结构的力学模型符合线性本构关系的假设。

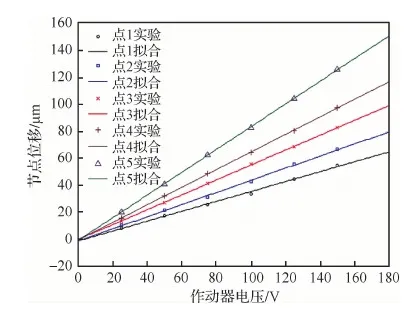
图15 反射面上5个点的位移Fig.15 Displacement of 5 points on reflector surface

3.2 有限元模型的实验验证

由于主控格栅反射器型面最优控制器的设计建立在有限元模型的基础之上，因此建立的有限元分析模型与真实物理系统的一致性将关系到型面控制实验的效果。将分析模型中每个PZT作动器加载50 V电压计算得到的反射面型面变形与真实样机的测试结果进行对比，图16为其中3个作动器加载50 V电压时型面变形误差云图的计算和实验结果。从图16可以看出，作动器在50 V 电压下产生的反射面形变云图计算结果和实验结果很接近。因此，证明了所建立的有限元模型的正确性，为进一步实现反射面的型面控制确立了基础。

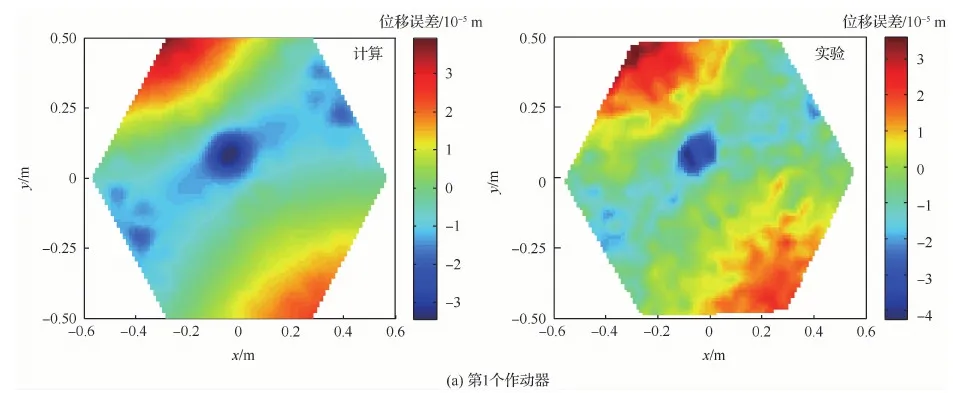
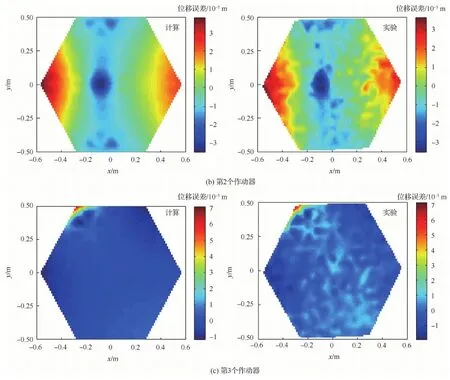
图16 反射面在不同作动器作用下位移误差云图Fig.16 Displacement error contours of reflector surface with different implementations of actuators

3.3 反射面初始制造误差的型面控制

CFRP复合材料格栅反射器的初始型面精度受到模具精度、固化成型中产生的应力的影响，因此，反射器的型面会存在一定的初始型面误差。本实验针对格栅反射器的初始型面误差，采用PZT压电作动器进行型面的主动调整。反射器的初始型面误差云图如图17所示。

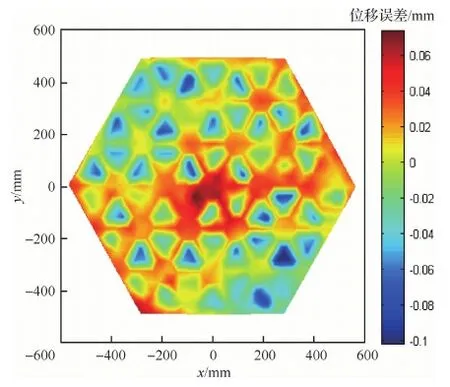
图17 反射器的初始型面误差Fig.17 Initial surface error of reflector

反射面的初始RMS误差为43.4 μm。运用72支PZT压电作动器对型面进行主动控制，控制后残余误差的分布云图计算分析与实验的结果如图18所示。从图18可以看出，控制后型面的残余误差云图，分析结果与实验结果比较接近。分析的残余RMS误差为17.8 μm。实验测量的残余RMS误差为19.5 μm，与计算结果较为接近，型面控制的效果显著。72支作动器相应的电压分布如图19所示。

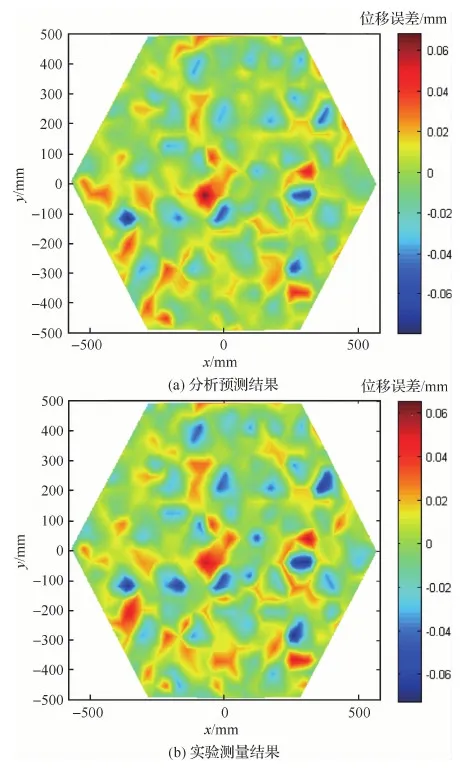
图18 控制后反射器型面的残余误差Fig.18 Residual error of reflector surface after control

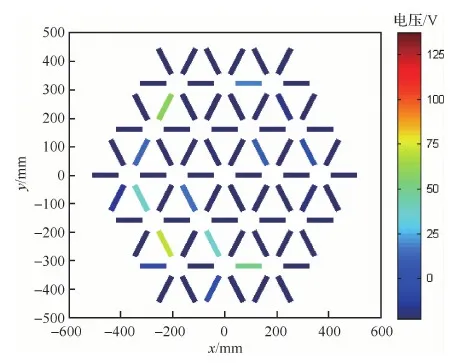
图19 主动型面控制的电压分布Fig.19 Distribution of voltages of active shape control

4 结 论

本文研究了CFRP格栅反射器的型面主动控制问题。从理论上建立了主控格栅反射器的有限元模型，基于建立的有限元模型提出了一种型面控制器的设计方法，并对PZT作动器的位置分布进行了优化。最后，搭建了相应的实验系统。进行了主控实验研究。本文的主要创新点可总结如下：

1) 设计了一种关于CFRP格栅反射器型面控制的方案，运用Hamilton变分原理推导了具有电压独立自由度、考虑高阶剪切形变的反射器有限元模型。

2) 基于平衡方程推导了型面最优控制器的表达式，反射器的型面控制问题转化为约束二次规划问题。

3) 对任意形式的载荷，将自适应遗传算法和梯度投影方法相结合，求解了限制作动器数量情况下的作动器位置分布和相应电压的问题。

4) 搭建了主控格栅反射器的实验系统。针对有限元模型的准确性以及对制造误差的控制效果进行了实验验证。

附录A

1) 板单元

板单元的形函数表达式为

(A1)

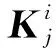
i=1,2,3,4

(A2)

2) 梁单元

梁单元的形函数矩阵可表示为

N′=[K′iK′j]

(A3)

子矩阵K′i和K′j可表示为

(A4)

式中:ξ′为梁单元的形函数参数；z′和y′为梁单元局部坐标系下的坐标；l为梁单元的长度。