二维三轴编织复合材料压缩失效行为的细观有限元模拟

刘鹏，郭亚洲，赵振强，邢军，张超,*

1. 西北工业大学 航空学院，西安 710072 2. 西北工业大学 陕西省冲击动力学及工程应用重点实验室，西安 710072 3. 中国民用航空适航审定中心，北京 100102

复合材料因其比强度高、比刚度大等优点，被越来越多地应用于航空航天、汽车和船舶等领域。编织复合材料因其成型便捷、抗损伤扩展性能优异，以及相比传统层合板更突出的抗冲击性能，近年来已经被广泛地用于制造大型飞机或发动机的结构部件。本文研究对象是二维三轴编织复合材料，作为一种富有潜力的织物复合材料，在航空航天和汽车等领域已经得到了一定的应用，例如美国通用电气公司在新一代大涵道比商用航空发动机GEnx中就使用了由二维三轴编织复合材料制成的全复合材料机匣[1]；由于二维三轴编织结构在冲击载荷下能量吸收效果良好，在汽车前纵梁上也得到了应用，Xiao等[2-3]开展了大量该复合材料管状试样的轴向抗冲击性能试验和仿真模拟方法研究。

在典型的0°/±60°二维三轴编织结构中，偏轴纤维束绕着轴向纤维束周期性交织在一起，0°纤维束呈直线状，并对应材料的轴向方向。通常，面内垂直于轴向方向定义为横向方向，垂直于轴向和横向组成的平面方向定义为厚度方向。因为编织结构比较复杂，二维三轴编织复合材料的破坏行为也比较复杂，为了研究这种材料的破坏机理，美国阿克伦大学的Littell[4]开展了4种不同树脂材料体系二维三轴编织复合材料试样在不同载荷条件下的力学试验研究，发现在横向拉伸载荷下，直边试样存在明显的自由边效应(Free-Edge Effect)，进而导致试验测得的性能不能反映材料的真实力学性能。为了克服自由边效应的影响，Kohlman[5]设计了非标准试验件，包括双边缺口试样和管状试样，并进行试验，其研究结果显示由于失效模式不稳定，仍难以得到理想的试验结果。近期Wehrkamp-Richter等[6]针对二维三轴编织复合材料进行了面内偏轴拉伸试验，发现二维三轴编织结构能够有效抑制裂纹扩展。总的来说，目前已开展的关于二维三轴编织复合材料的试验研究中，仍以拉伸试验为主，因压缩试验夹具相对复杂且失效机理不明确，关于压缩的研究尚不充分。Quek等[7]开展了0°/±45°二维三轴编织复合材料双轴压缩试验研究，该试验消除了上述试验中存在的自由边效应，并发现该复合材料压缩失效主要由纤维束弯曲和界面失效引起。

受限于材料复杂的编织结构，通过试验很难直接观察复合材料内部的损伤演化过程，而数值模拟方法可以弥补上述的不足，通过对材料细观结构的模拟、局部的损伤分析，结合有限元软件可视化模块，可以直观地分析复合材料的渐进损伤过程，也可以大幅地降低试验费用。有关二维三轴编织复合材料的数值仿真，近年来也一直有学者进行研究。最初，Cheng[8]提出了一种Subcell模型，将二维三轴编织复合材料的单胞等效为四个复合材料层合板单元，模拟了该材料在高速冲击载荷下的力学响应和失效形貌。在其基础上，Binienda等[9-11]对该模型进行了不断优化和改进，但由于该模型无法反映材料的细观几何特性，导致其无法应用于分析具体的失效机理。细观有限元模型通过对基体、纤维束和界面等主要构成的组分分别建模，可详细地模拟和预测各组分损伤的起始和扩展过程。Waas等[12-14]建立了细观单胞模型，采用ABAQUS软件里弧长法(Riks Method)来模拟纤维束初始缺陷并进行有限元仿真，探讨了纤维束不同的弯曲模式和初始缺陷对材料整体压缩强度的影响，并进一步研究了不同尺寸模型纤维束弯曲模式和破坏情况的差异性。Zhang等[15]基于0°/±60°二维三轴编织复合材料的真实几何尺寸，建立了一套编织复合材料的细观有限元模拟方法体系，利用内聚力界面单元(Cohesive Element)模拟了纤维束之间以及纤维束与基体之间的界面失效，并深入研究了边界效应形成的机理以及其对直边试样测试性能的影响规律。基于此细观有限元模型，Zhao等[16]发展了此材料的多尺度仿真方法，采用细观-宏观均一化方法来获取宏观亚单胞模型的性能参数，继而用于分析材料在高速冲击载荷下的失效行为和破坏模式。

目前针对二维三轴编织复合材料压缩性能的研究相对较少，Waas[12-14]与Li[17]等针对二维三轴编织复合材料建立的细观有限元模型仅包含一个或数个单胞，模型尺寸与真实试样尺寸存在较大差异，而Zhang[18]和Zhao[19]等的研究表明二维三轴编织复合材料在面内和厚度方向都具有明显的尺寸效应，采用单个单胞或单层模型很难预测材料真实的力学响应。因此，本文基于细观有限元模拟方法，建立了和实际试样等宽的有限元模型，结合复合材料渐进损伤模型和内聚力界面模型，采用ABAQUS/EXPLICIT求解器，结合VUMAT子程序，模拟了在轴向和横向压缩载荷下二维三轴编织复合材料的损伤起始和扩展过程，分析了纤维束波动对压缩性能的影响规律，提出了该材料细观有限元压缩模型的分析策略。

1 材料与试验

本文所研究的二维三轴编织复合材料由美国A&P公司制备，通过树脂传递模塑成型技术制造成型，轴向纤维束是T700-24K碳纤维，偏轴纤维束是T700-12K碳纤维，基体是增韧环氧树脂Epon862。如图1所示，0°方向为轴向纤维束，偏轴纤维束分别沿±60°方向上绕轴向纤维束周期性地交织穿插。

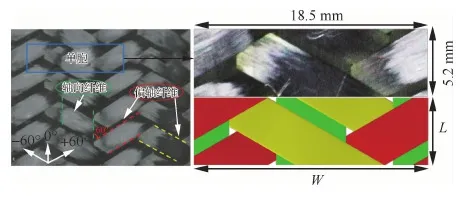
图1 二维三轴编织布的平面结构图Fig.1 Architecture of two-dimensional triaxially braided carbon fabrics

从制造商和文献[4,17]中得到了T700碳纤维和树脂基体的基本力学性能，列于表1中。二维三轴编织复合材料的性能测试试验数据全部是由Littell[4]使用MTS-858拉扭试验机完成的，加载速率为0.010 6 mm/s，试样为参照ASTM-D3410标准设计的直边试样，宽度为35.8 mm，长度为152.4 mm，标距段长度为25.4 mm，分为轴向压缩和横向压缩两种类型。

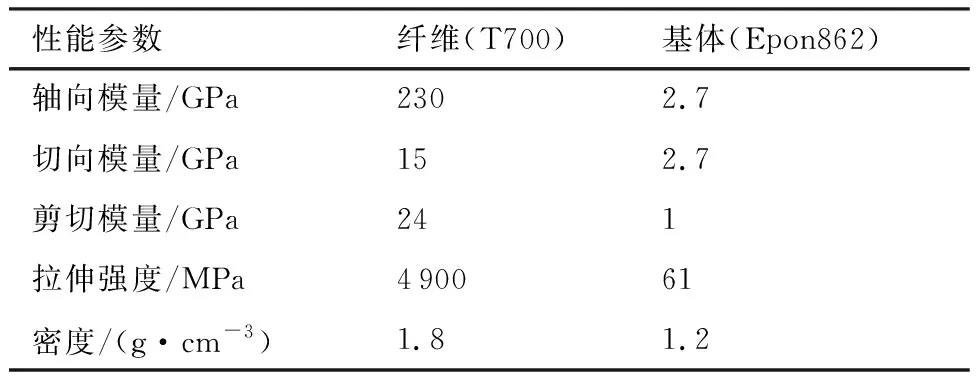
表1 纤维和基体的力学性能Table 1 Mechanical properties of fiber and matrix

2 细观有限元模型

细观有限元模型能够准确描述纤维织物的几何特性，包括纤维束的分布和局部的弯曲波动，在此基础上结合复合材料损伤判据，进而可预测每种组分的力学响应以及他们对整体性能的影响，同时可有效地表征材料在不同载荷下的损伤情况[20]。通过对一个单胞或多个单胞的仿真与分析，能够得出各组分的应力分布以及失效模式，从而可以对材料各组分在相应加载情况下的损伤起始与扩展情况进行准确预测。

2.1 单胞的几何参数

二维三轴编织复合材料可以看成由此材料结构的最小重复单元(简称为单胞)在各方向上通过周期性堆叠形成，因此在细观尺度上需要对单胞的几何参数进行详细的描述。如图1所示，单胞的宽度W为两个相邻轴向纤维束的中轴线的间距；单胞的长度L为同一方向相邻偏轴纤维束的中轴线的间距；单胞的厚度H为单层编织复合材料试样的平均厚度。根据Zhang等[15]的微观表征和计算，轴向纤维束和偏轴纤维束的纤维体积分数分别为vfa和vfb，单胞总体纤维分数为vf，具体参数在表2中列出。在编织复合材料的制备成型过程中，各纤维束会相互挤压，导致轴向纤维束产生微小的起伏，但相对于偏轴纤维束的起伏程度，轴向纤维束起伏程度较小。为了便于建模，本研究在几何上假定轴向纤维束呈直线状，偏轴纤维束绕轴向纤维束穿插编织。同时，为了考虑轴向纤维束起伏波动的影响，本文基于坐标转换计算对轴向纤维束的等效刚度进行了折减，详细细节在后文中介绍。

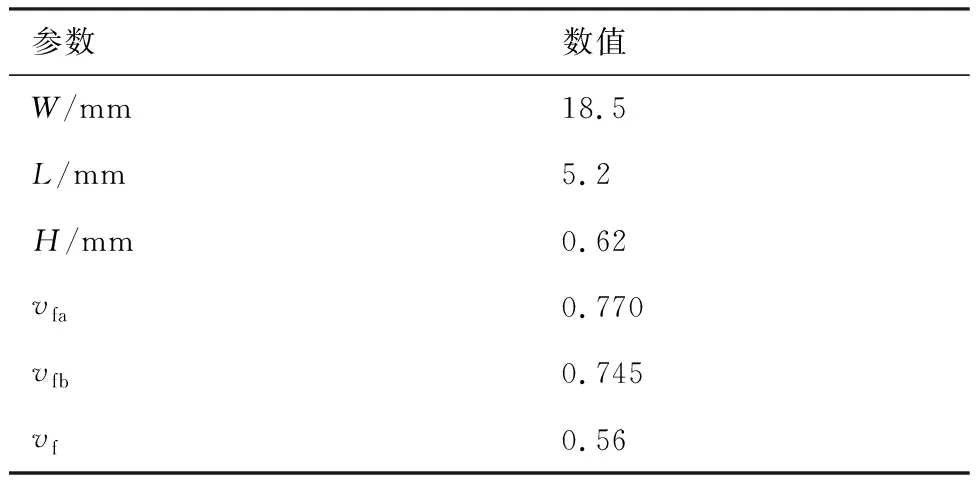
表2 二维三轴编织复合材料单胞的几何参数

2.2 单胞的有限元模型

首先，使用TexGen软件，生成如图2(a)所示的二维三轴编织复合材料的单胞几何模型(为了更好显示纤维束编织结构，此处将基体设置为透明)，纤维束横截面假定为理想椭圆形状；然后，通过TexGen生成如图2(b)所示有限元模型，模型中纤维束和基体部分的网格节点能够一一对应。此外，为了模拟纤维束间和纤维束与基体的界面，在纤维束表面建立了一层厚度为10-4mm的内聚力单元(Cohesive Layer)，如图2(c)所示，界面单元以共节点的形式连接纤维束和基体部分。单胞模型中所有单元均为八节点六面体单元，沿其轴向(y方向)有26个单元，横向(x方向)有52个单元，厚度方向(z方向)有10个单元。虽然在此模型中，偏轴纤维束的边缘存在阶梯状的起伏单元，但由于其网格大小均匀合理，消除了四面体的单元可能存在的应力集中问题，所以整体模拟效果比四面体单元模型更佳。

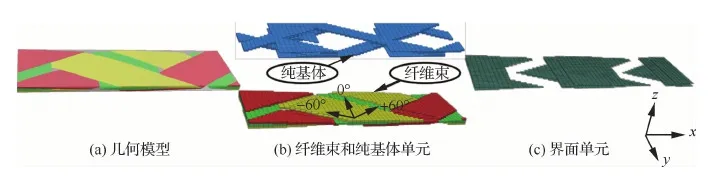
图2 二维三轴编织复合材料单胞的有限元模型Fig.2 Finite element model for unit cell of two-dimensional triaxially braided composite

2.3 边界条件

对于有限元分析来说，应用合适的边界条件对于求解至关重要。本文开展了轴向压缩和横向压缩两种加载条件的仿真研究。为了保持模型尺寸和试验的一致性，同时保证有限元模型里面单胞的完整性，采取了如图3所示的模型，图中a和b分别为有限元单胞模型的宽度和长度。轴向压缩时，试样沿着y方向加载，采用如图3(a)所示的模型，其x方向(垂直轴向纤维束方向)上有2个单胞，尺寸为37.00 mm，与试验尺寸相接近；为了减小计算量，y方向(加载方向)上有2个单胞，尺寸为10.34 mm；z方向(厚度)上有6个单胞，尺寸为3.72 mm，与试验试样厚度相同。横向压缩时，沿着x方向加载，其模型尺寸如图3(b) 所示，y方向(轴向纤维束方向)上有7个单胞，尺寸为36.19 mm，与试验尺寸相接近；x方向上有1个单胞，尺寸为18.5 mm；z方向(厚度)上有6个单胞，尺寸为3.72 mm。

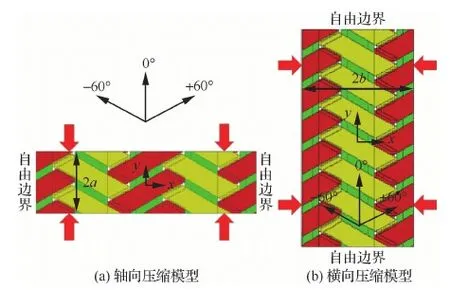
图3 轴向和横向压缩有限元模型(只显示纤维束)Fig.3 Axial and transverse compression finite element models (only show fiber bundles)

在加载时，在单元网格外设置一个参考点REF，通过控制REF的位移实现两端对称加载。

轴向压缩时边界条件为

(1)

横向压缩时边界条件为

(2)

式(1)～式(2)中：U1和U2分别为x和y方向上的位移。

3 材料的力学本构

第2节介绍的二维三轴编织复合材料的细观模型包含纤维束、纯基体和界面3个部分。其中，基体材料Epon862为一种增韧环氧树脂材料，其在压缩载荷下的力学响应可以用弹性-理想塑性模型来表征[21]。由于基体材料的压缩失效应变远大于纤维束的失效应变，因此本研究中没有考虑纯基体材料的失效。以下分别对纤维束和界面的材料模型进行详细介绍。

3.1 纤维束渐进损伤模型

编织复合材料中的纤维束，通常可以等效成横观各向同性的单向复合材料板，其本构方程为

σij=Cijklεkl

(3)

式中:σij、Cijkl和εkl(i，j，k，l= 1，2，3)分别为工程应力、刚度系数和工程应变，下标1、2、3分别指纤维束的轴向、横向和面外方向。Eij、μij和Gij为材料的工程常数，根据横观各向同性假设，可以得到：E22=E33，μ12=μ13，G12=G13。在满足某个失效判据前，材料为线弹性。

3.1.1 失效判据

本文根据Hashin[22]和Hou等[23]的失效判据建立了纤维束的三维破坏准则，包含纤维拉伸、纤维压缩、基体拉伸和基体压缩4种失效模式。

纤维拉伸失效(σ11>0)：

(4)

纤维压缩失效(σ11<0)：

(5)

基体拉伸失效(σ22>0)：

(6)

基体压缩失效(σ22<0):

(7)

式(4)～式(7)中：eft、efc、emt、emc为表征材料损伤程度的量；F1t、F1c、F2t、F2c、Fls、Fts分别为纤维束的轴向拉伸强度、轴向压缩强度、横向拉伸强度、横向压缩强度、纵向剪切强度和横向剪切强度;系数α用来衡量剪切应力对纤维拉伸失效的贡献。

3.1.2 损伤演化模型

一旦某种损伤起始准则条件满足，继续加载则会引起材料刚度下降，Zhang等[15]对此模型有详细的描述。该损伤模型在损伤演化表达式中引入了一个特征单元长度(体单元体积的三次方根)，将单元断裂能表示为

(8)

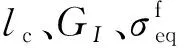
(9)

(10)

(11)

对于复合材料来说，由于其在最终破坏前有一个损伤逐渐积累，材料性能逐渐退化的过程，目前采用连续损伤模型预测复合材料渐进损伤的方法已被普遍接受，为了描述从无损伤到完全失效这一过程，本文采用二阶对称张量描述纤维束的损伤状态，损伤状态的柔度矩阵S(d)的形式为

S(d)=

(12)

式中：df=(1-dft)(1-dfc)为纤维损伤变量，dft和dfc分别为纤维拉伸、纤维压缩对应的损伤变量；dm=(1-dmt)(1-dmc)为基体损伤变量，dmt和dmc分别为基体拉伸和基体压缩对应的损伤变量。

dI(I=ft，fc，mt,mc)用来衡量材料不同失效模式的损伤程度，其变化范围为(0，1)。未加载时dI初始值为0，表示材料完好未出现损伤；在加载过程中，当满足相应的失效判据后，dI值会逐渐增大，材料刚度会相应逐渐降低，当dI增大到1时，则表示单元已完全失效，材料参数退化的详细说明参见文献[24]。

上述针对纤维束损伤起始及演化行为的三维渐进损伤模型通过编译ABAQUS用户自定子程序VUMAT实现，并结合ABAQUS/EXPLICIT求解器进行求解运算。

3.1.3 纤维束刚度和强度预测方法

现有预测纤维束刚度的方法，如混合准则、桥联模型和Chamis模型[25]等理论模型都是预测材料在弹性阶段的响应，预测公式类似且结果接近,本文采用Huang[26-27]的桥联模型来确定纤维束的刚度参数。

(13)

式中：[dσi]=[dσ11dσ22dσ33dσ23dσ13dσ12]T;上标f和m分别表示纤维和基体;[Aij]为桥联矩阵，文献[28]对此有详细说明。

[dεi]=[Sij][dσj]

(14)

式中：[dεi]、[dσj]和[Sij]分别为纤维束的应变、纤维束应力和纤维束的柔度矩阵，通过推导可得出纤维束的柔度矩阵表达式为

(VfI+Vm[Aij])-1

(15)

其中：Vf和Vm分别为纤维束里纤维和基体的体积分数；I为单位矩阵。通过纤维束的柔度矩阵，可以求出纤维束的刚度，进而可通过改进的桥联模型[28]求出纤维束的强度。

由于改进的桥联模型推导纤维束1方向(轴向)压缩强度F1c时，只考虑了纤维压缩失效，这会导致理论值比实际值偏大。同时，纤维束波动、孔隙率等几何缺陷对纤维束的压缩强度也会有一定的影响，因此，本文采用参数分析的方式来确定纤维束的压缩强度。

3.1.4 纤维束力学参数

由于成型过程中，层间的错位和相互挤压使得材料在厚度上更为紧凑，多层编织复合材料试样在几何结构上和理想化的几何模型会有一定的差异性。因此，数值模型中纤维束的纤维体积分数必须进行略微调整，才能使得整个单胞的纤维体积分数与真实试验(56%)保持一致。Zhao等[16]研究了六层二维三轴编织复合材料单胞模型中轴向纤维束和偏轴纤维束的纤维体积分数，分别为86%和69%。

基于3.1.3节所述方法，分别得到了轴向和偏轴纤维束的力学性能参数，如表3与表4所示。本文数值模型中所用材料断裂能的值引用自Li等[17]的工作，其具体的值如表5所示，Gft、Gfc、Gmt和Gmc分别为纤维拉伸、纤维压缩、基体拉伸和基体压缩的断裂能。

表3 轴向纤维束(vfa=86%)和偏轴纤维束(vfb=69%)的弹性常数

Table 3 Elastic constants of axial fiber bundles (vfa=86%) and bias fiber bundles (vfb=69%)

弹性常数数值vfb=69%vfa=86%E11/GPa159.5165.5E22/GPa8.3111.24E33/GPa8.3111.34μ120.310.30μ130.310.30μ230.530.51G12/GPa4.58.5G13/GPa4.59.0G23/GPa2.73.7

表4 轴向纤维束(vfa=86%)和偏轴纤维束(vfb=69%)的强度参数

Table 4 Strength parameters of axial fiber bundles (vfa=86%) and bias fiber bundles (vfb=69%)

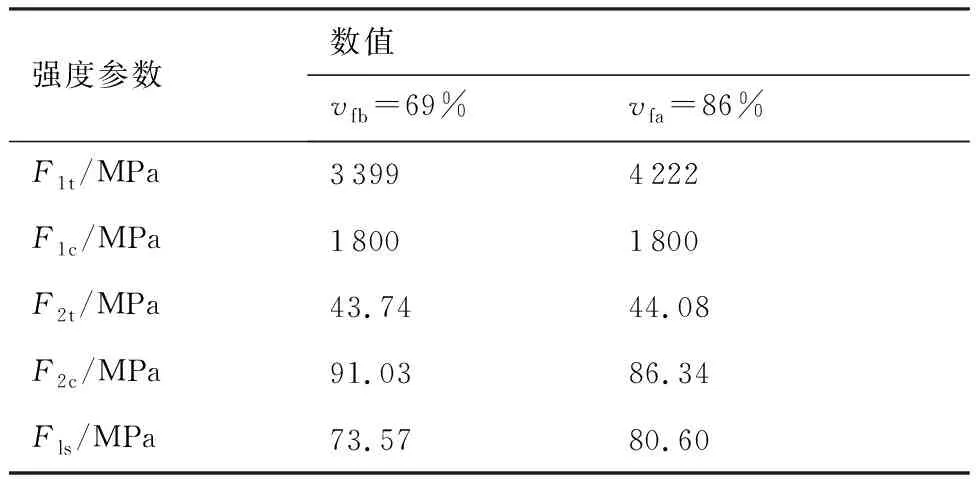
强度参数数值vfb =69%vfa =86%F1t/MPa33994222F1c/MPa18001800F2t/MPa43.7444.08F2c/MPa91.0386.34Fls/MPa73.5780.60

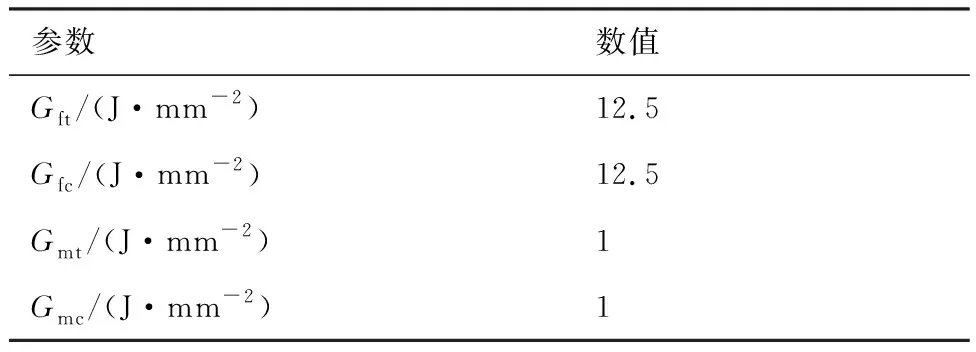
表5 纤维束的断裂能参数Table 5 Fracture energy parameters of fiber bundles

3.2 轴向纤维束的刚度折减

如2.1节所讨论，实际的二维三轴编织复合材料试样，由于偏轴纤维束的挤压，会导致轴向纤维束产生一定程度的起伏，如图4(a)[29]所示。这些纤维束的起伏波动会影响整个试样件的等效模量，也会对材料的压缩强度造成影响。因此，本文引入了波动幅度参量，对纤维束的刚度进行折减，以考虑纤维束波动对宏观压缩性能的影响。

图4 轴向纤维束波动的截面照片和等效图[29]Fig.4 Microscope image and representation of axial fiber bundle undulation [29]

如图4(b)所示，轴向纤维束总体延伸方向为y轴，垂直于y轴方向为z轴，据此定义总体坐标系；沿着轴向纤维束的中轴线方向为2轴，垂直2轴方向为3轴，据此建立局部坐标系。首先，求出轴向纤维束中轴线上每一点的局部刚度矩阵Clocal。假设轴向纤维束中心波动符合余弦函数，每个单胞内有一个完整的余弦波长，则轴向纤维束中轴线在总体坐标系上的表达式为

(16)

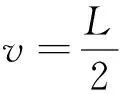
(17)

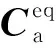
同时，引入轴向纤维束波动系数r:

(18)

据此，可以计算纤维束波动所造成的等效刚度折减，进而可分析其对压缩性能的影响。

3.3 界面损伤模型

纤维束-纤维束界面和纤维束-纯基体界面的失效行为是编织复合材料的主要损伤模式之一[29]。目前主要有3种分层模拟方法：基于失效准则模型、断裂力学方法和界面单元建模方法。第1种方法是把分层作为失效准则中的一种失效模式，如Hou等[23]所采用的3D失效准则，这种方法计算效率高，但分层界面不是单独存在而且也没有明确的建模。第2种方法，需要预先知道破坏的具体位置，并且对于三维问题，计算量很大。而最近开发的第3种方法已经被广泛地运用于有限元分析中的界面单元，这种方法不需要知道初始裂纹的具体信息，能准确地模拟裂纹萌生与裂纹扩展。

为了模拟纤维束间的界面，本文应用了厚度为10-4mm的内聚力(Cohesive)单元，关于Cohesive单元的理论公式可参考ABAQUS帮助文件[30]及文献[31]。本文采用了二次名义应力准则来判断损伤的起始，其表达式为

(19)

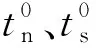
(20)

表6 界面强度和界面韧性参数[17]

Table 6 Parameters for interface strength and fracture toughness[17]

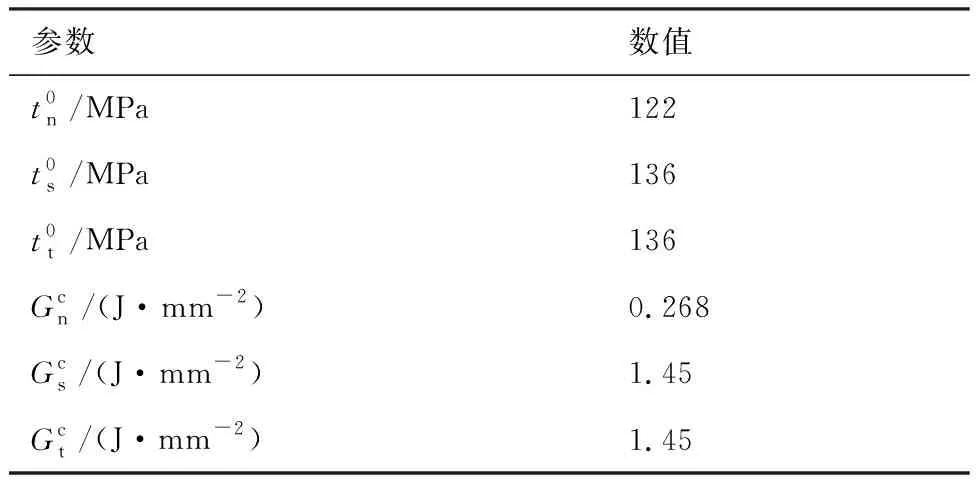
参数数值t0n/MPa122t0s/MPa136t0t/MPa136Gcn/(J·mm-2)0.268Gcs/(J·mm-2)1.45Gct/(J·mm-2)1.45

4 结果分析

4.1 模型验证

本文通过对比仿真预测和试验测得的应力-应变曲线，来验证模型的准确性。图5(a)和图5(b) 分别对比了轴向压缩和横向压缩载荷下的应力-应变曲线，其中应力为加载横截面上的反作用力之和与初始横截面面积的比值，应变为加载方向的伸长量与初始长度的比值。同时，通过0～0.5%应变范围内应力-应变曲线的初始斜率可获得等效模量。

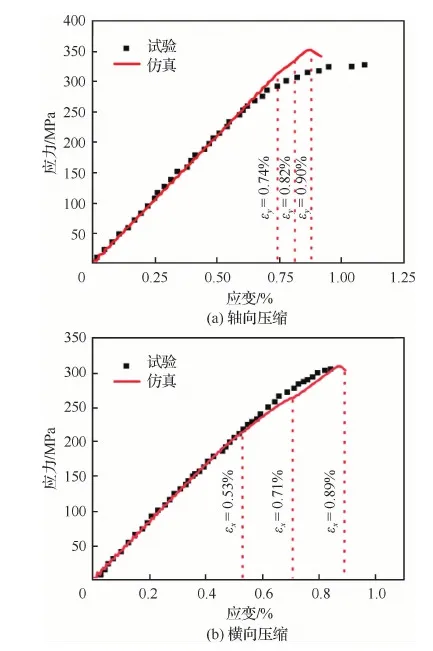
图5 仿真和试验的应力-应变曲线比较Fig.5 Comparison of numerically predicted and experimentally measured stress-strain curves

在较低的应变水平(<0.5%)下，轴向压缩与横向压缩的应力-应变曲线基本保持线性，无明显损伤行为，且仿真与试验曲线拟合得很好。随着加载的进行，图5(a)所示轴向压缩试验曲线在后半段出现了较大的非线性，而仿真曲线则无显著刚度退化。这是因为，由于成型工艺的影响，实际试样中轴向纤维束会受到不同层纤维束的挤压，会不可避免地产生纤维束波动，而在轴向压缩载荷下纤维束波动会变得更为显著，导致屈曲和严重的分层失效。Littell[4]在其轴向压缩试验中也观察到纤维束出现屈曲现象，Sun等[32]从微观角度讨论了在压缩载荷下纤维丝的屈曲响应。另一方面，由于本文细观模型的局限性，轴向纤维束被认为呈直线状，难以反映纤维束弯曲所导致的非线性应力应变响应，因而形成了试验与仿真曲线在非线性段的差异性。

图5(b)所示的横向压缩应力-应变曲线整体吻合情况优异。与轴向压缩相比，在横向压缩载荷时，轴向纤维束由于与加载方向垂直，承担载荷相对较少，因此轴向纤维束起伏的影响也相对较小，宏观应力-应变曲线的非线性也相对较弱。图5(b)中，在εx=0.71%时，仿真模型预测偏轴纤维束交错区域发生纤维束基体压缩损伤，导致试样等效刚度略微下降,但纤维束中并未出现纤维损伤，模型仍能继续承载直至出现纤维断裂失效。

表7对比了轴向压缩和横向压缩两种载荷下，试验测试及仿真预测的初始模量和压缩强度。Ey和Ex分别表示沿着轴向和横向的初始模量，σy和σx表示沿着轴向和横向的压缩强度。横向压缩载荷下，仿真和试验的Ex和σx十分接近，误差在3%以内；轴向压缩载荷下，仿真和试验的Ey十分接近，σy相差较大，但误差在10%以内。通过图5和表7，可以认为本文所建立的细观有限元模型的准确度高，可应用于材料内部的损伤机制分析。

表7 仿真和试验的初始模量和压缩强度对比

Table 7 Comparison between numerical predicted and experimental measured initial tangent modulus and compression strength

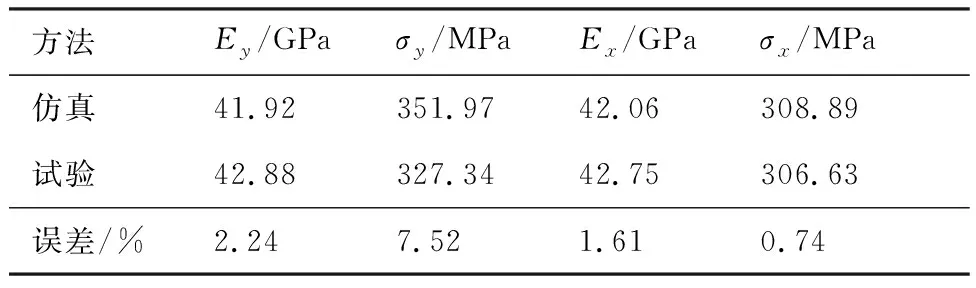
方法Ey/GPaσy/MPaEx/GPaσx/MPa仿真41.92351.9742.06308.89试验42.88327.3442.75306.63误差/%2.247.521.610.74

4.2 损伤分析

细观有限元模型的优点是能清晰地表征材料内部各组分(包括纤维束、基体和界面)损伤起始和演化的过程，通过有限元软件后处理模块，可得到不同载荷水平下局部应力、应变和损伤等力学响应的云图，进而可对材料的失效机理进行详细的分析。

4.2.1 轴向压缩

图6显示了纤维束中纤维、基体和纤维束间界面以及层间界面的损伤情况。损伤程度可根据颜色来区分，损伤数值0表示没有损伤，1表示已经完全失效，0到1之间是损伤积累阶段。为了研究渐进损伤机制，对3个典型全局应变下的损伤情况进行了对比分析。当应变εy=0.74%时，偏轴纤维束在交错互锁区域率先出现基体压缩损伤，仿真应力-应变曲线开始出现非线性；同时，在同一区域纤维束-纤维束间有少量的Cohesive单元也出现损伤。为了研究相应的损伤机理，取出现损伤前的应力状态来分析，图7显示了在轴向压缩应变εy=0.70%时，各纤维束的应力云图，包括σ11、σ22和σ12(1表示x方向，2表示y方向)。在图7中，偏轴纤维束在交织互锁区域受压缩载荷时收缩方向不同，会存在比较大的面内切应力σ12；同时因为此区域没有轴向纤维束，载荷主要由偏轴纤维束传递，所以偏轴纤维束在此处的σ22会相比较于别处稍大。两者共同作用下，模型中此区域会率先出现上述两种损伤。当εy=0.82%时，在偏轴纤维束交织互锁区域，纤维束基体压缩

图6 轴向压缩损伤分布云图Fig.6 Damage distribution contours of axial compression simulation

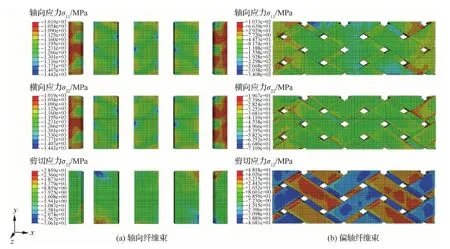
图7 轴向压缩应力分布云图(εy=0.70%)Fig.7 Stress distribution contours of axial compression simulation (εy=0.70%)

损伤和层内Cohesive单元损伤逐渐积累并沿横向扩展。

在应变εy=0.90%时，轴向压缩应力-应变曲线(见图5(a))开始卸载，由图6可见轴向纤维束出现纤维压缩损伤，但偏轴纤维束并未出现纤维压缩损伤。如图7所示，在轴向压缩载荷下，轴向纤维束所承受的应力σ11是偏轴纤维束应力σ11的3倍左右，意味着轴向纤维束是主要承载组分。因此，一旦轴向纤维束出现纤维压缩破坏，编织复合材料试样整体承载能力会快速退化导致试样断裂和卸载。由图6可见，在εy=0.90% 时，轴向纤维束出现纤维压缩失效的区域，也出现了基体压缩破坏以及层内和层间Cohesive单元损伤积累，这是由于此处纤维束压缩破坏后，局部刚度降低，而出现了应力集中和损伤的快速扩展。

4.2.2 横向压缩

与轴向压缩相比，横向压缩的损伤过程和破坏行为更为复杂，其主要破坏形式是轴向纤维束的基体压缩失效和偏轴纤维束的纤维压缩失效，同时在模型中观察到了由于自由边效应造成的边界区域损伤。图8显示了横向压缩载荷下纤维束中纤维、基体和纤维束间界面以及层间界面的损伤情况。

在应变εx=0.50%时，图9显示了对应横向压缩载荷下局部应力云图。通过比较图9中轴向纤维束的σ11和σ22，可以观察到由于轴向纤维束与加载方向垂直，它的切向方向(垂直纤维束方向)会受到较大的正应力；同时轴向纤维束在与偏轴纤维束接触区域会受到后者施加的应力。在两者共同作用下，应变εx=0.53%时，图8中轴向纤维束在此区域出现了大量的基体压缩损伤，这给图5(b)横向压缩的应力-应变曲线带来非线性，但是轴向纤维束与加载方向垂直，没有贯穿加载方向，不是承担载荷的主要组分，其损伤不会导致纤维束最终的破坏。由于自由边效应的影响，观察到在图9中偏轴纤维束在自由边附近的σ11、σ22和σ12应力值相比于其他区域较大，因此在图8中观察到偏轴纤维束在自由边附近率先出现了基体压缩损伤。

随着压缩载荷的持续增加，偏轴纤维束基体压缩损伤沿着纤维束方向不断扩展，对应图5(b)中横向压缩的应力-应变曲线开始出现一定程度刚度下降。此外，由于自由边效应的影响，在应变εx=0.71%时，图8中自由边附近的层间Cohesive单元也开始出现损伤。同时，偏轴纤维束在交织区域因为受到压缩载荷时收缩方向不一致，这一区域层内Cohesive单元进而开始进入损伤积累阶段，并沿着这一区域不断扩展。

在应变εx=0.89%时，偏轴纤维束开始出现纤维压缩损伤，同时应力-应变曲线开始卸载。与轴向压缩时的受力情况不同，偏轴纤维束是受横向压缩载荷时的关键组分，此外，由于与加载方向垂直，轴向纤维束中并没有出现纤维失效，因此偏轴纤维束的纤维压缩破坏对应复合材料试样的最终压缩失效。另一方面，层内和层间Cohesive单元的损伤行为在区域和扩展路径上，也明显的显现出与偏轴纤维束损伤情况的相关性，如图8所示。

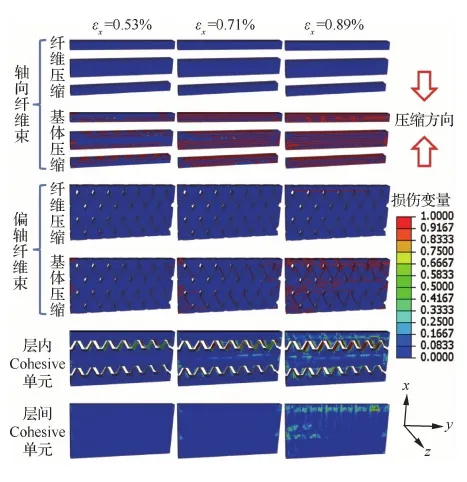
图8 横向压缩损伤分布云图Fig.8 Damage distribution contours of transverse compression simulation

4.3 轴向纤维束波动幅度对压缩刚度的影响

为了进一步地研究纤维束波动对压缩性能的影响，本文通过在细观有限元模型中考虑波动所导致的纤维束刚度折减，研究了波动系数r对宏观力学响应的影响规律。

图10(a)对比了不同波动系数所对应的轴向压缩应力-应变曲线。图10(b)展示了轴向纤维束的轴向(沿着纤维束方向)模量E11、编织复合材料的轴向初始模量Ey和轴向压缩强度σy随着r的变化趋势图。通过与试验测得的模量对比，本文选取轴向纤维束波动系数r=0.05。

从图10(b)中可以看出，Ey和E11随着r值的增加呈现线性的下降趋势，这表明轴向纤维束的波动对材料轴向压缩刚度有着显著的影响，在仿真模拟和设计分析中需要予以考虑。另一方面，由图10(a)和图10(b)可见，随着r值的增加，尽管曲线斜率不断下降，但强度值变化较小，这是因为此模型是采用基于应力的失效判据，而纤维束波动并不会直接影响纤维束本身的强度值，所以试样能够承受的破坏载荷变化不大。仿真结果中强度的略微变化主要是由于纤维束波动引起的刚度变化，以及其所造成的整体应力应变分布的差异性。在横向压缩过程中，轴向纤维束不是主要承载组分，因此轴向纤维束的波动对横向压缩模量几乎没有影响。

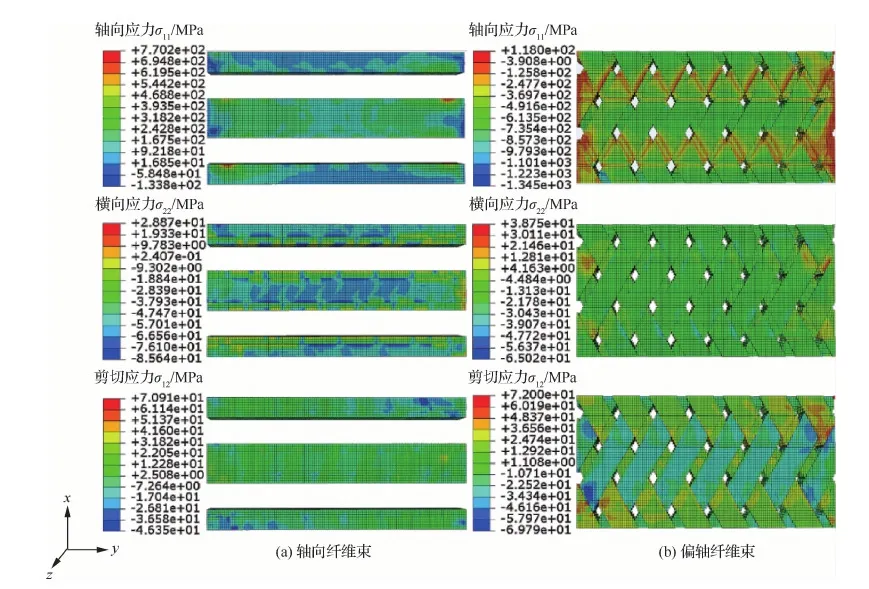
图9 横向压缩应力分布云图(εx=0.50%)Fig.9 Stress distribution contours of transverse compression simulation (εx=0.50%)

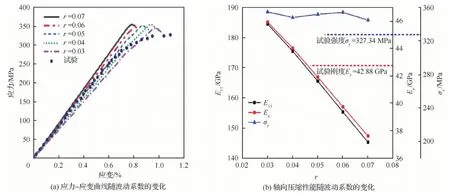
图10 波动系数对轴向压缩性能的影响Fig.10 Influence of undulation coefficient on axial compression performance

4.4 纤维束压缩强度对压缩损伤的影响

4.3节分析了轴向纤维束波动所导致的刚度折减对二维三轴编织复合材料压缩性能的影响，而未考虑纤维束强度的影响。目前，尚无完善的关于纤维束压缩强度的理论预测和测试方法，本文所选取的压缩强度参数通过模型校正获得。轴向和偏轴纤维束轴向压缩强度F1c取1 400、1 600、1 800、2 000、2 200 MPa 这5个数值，图11中展示了轴向和偏轴纤维束的F1c分别与编织复合材料轴向和横向压缩响应的相关性。

从图11中可以看出，轴向压缩强度σy与轴向纤维束的F1c呈现正相关关系，在一定范围内，偏轴纤维束的F1c对轴向压缩强度σy没有影响；同时，横向压缩强度σx与偏轴纤维束的F1c呈现正相关关系，在一定范围内，轴向纤维束的F1c对横向压缩强度σx没有影响，这进一步说明了轴向压缩破坏是由轴向纤维束纤维压缩失效主导，横向压缩破坏由偏轴纤维束纤维压缩破坏导致。通过与试验结果对比校正，本文模型里轴向和偏轴纤维束的F1c都取为1 800 MPa。

图11 纤维束强度F1c对压缩性能的影响Fig.11 Influence of fiber bundle strength F1c on compression performance

5 结 论

1) 本文建立的二维三轴编织复合材料的细观有限元模型，准确地预测了该材料在准静态压缩载荷下的力学响应和渐进损伤失效过程。

2) 二维三轴编织复合材料轴向压缩的破坏是由轴向纤维束的纤维压缩失效主导；横向压缩破坏则由偏轴纤维束的纤维压缩失效引起。

3) 在轴向压缩过程中，分层现象不明显，而在横向压缩过程中，有着明显的分层现象以及自由边效应。

4) 轴向纤维束的波动对轴向压缩性能有着明显的影响。通过数值参数分析，本模型中轴向纤维束波动系数取0.05，纤维束压缩强度为1 800 MPa。