直升机旋翼电磁特性模拟新技术

郭杰，殷红成，叶尚军，满良，贾崎

1.电磁散射重点实验室，北京 100854 2.中国航天科工二院，北京 100854 3.浙江大学 航空航天学院，杭州 310027

直升机是低空复杂环境的重要威慑力量[1]，因此在试验中，出于经济性和易用性考虑，通常采用小型无人直升机靶标对其进行模拟，比如美国的“Mi-4UM”直升机靶标[2-3]。靶标需要对真机的外形尺寸、飞行机动特性和电磁、红外目标特性等进行有效模拟。对于直升机来说，其电磁散射特性是主要模拟对象[4]。

直升机的电磁散射特性，也就是雷达探测直升机所产生的回波，主要源于机身、旋翼和尾桨这3部分，其中机身和旋翼是最主要的散射源[5-6]。对于悬停或者低速掠地飞行的直升机，采用多普勒体制的雷达主要通过探测桨叶旋转的调制特性对其进行侦查和预警。因此对直升机桨叶电磁散射特性的模拟具有非常重要的实战意义[7-8]。

小型无人直升机靶标旋翼的展长和弦长较小，为了有效模拟真机的电磁散射特性，需要对其进行雷达回波增强，而由于桨叶结构、气动布局、挥舞特性等诸多因素的限制[9-10]，这方面的工作一直是直升机特性无源模拟的一个技术难题，相关的研究成果鲜有报导。目前研究工作主要集中于直升机电磁特性的仿真和测试方面[11-12]。Amor-Martin等利用非标准网格截断技术开发了一种基于有限元法的内部电磁代码，在高性能计算系统中对直升机的雷达散射截面进行了数值计算[13]；Karabayir等基于直升机的计算机辅助模型，在各种螺旋桨或桨叶转速下从理论上分析了直升机的微多普勒特征，并将之用于空中目标的分类[14]；Zhou等基于Pareto解的方法建立了一个气动噪声和雷达隐身的旋翼模型优化方法[15]；Chen建立了桨叶回波简单叠加的主旋翼回波模型[16]；贺治华在旋翼单频回波模型的基础上提出了宽带调频回波模型[17]；林刚对直升机的动态散射特性进行了分析，并通过桨叶散射模型对散射中心的周期性运动调制效应进行了讨论[18]；朱迪给出了双基地雷达情形下旋翼的回波模型[19]。

基于直升机桨叶的结构特点和雷达回波特性，本文提出一种基于小散射源阵列的新型旋翼散射特性增强技术，对小型无人直升机靶标旋翼目标特性进行模拟，并通过微波暗室试验对其进行分析评估，为试验模拟提供技术支持。

1 目标特性增强原理

目标的电磁散射强度可以通过加载金属角反射器，龙伯透镜反射器，介质球等无源方式来提高[20-22]。然而直升机桨叶的厚度一般为几个厘米，与波长相近，采用传统的单个散射源，其增强能力非常有限。如果将N个小散射源等距排成一个阵列，如图1所示，依次编号为0,1,…,k,…,N-2,N-1，每一小散射源可称为一个阵元，阵元间距记为d。假设第k个阵元的雷达散射截面(Radar Cross Section, RCS)为σk，其与雷达接收机的距离为rk，则整个阵列总的RCS就是各阵元RCS之和，即[23]

(1)

式中：λ为入射雷达波波长。

若雷达波入射方向与阵元最大回波增益方向夹角为θ，第0号阵元距离雷达接收机r0，第k号阵元距离雷达接收机rk，则经简单推导可得

rk=r0+kdsinθ

(2)

式中：θ∈[-π/2,π/2]。

图1 小散射源阵列示意图Fig.1 Schematic diagram of small scattering source array

假设各阵元RCS相等，表示为σ0，将σk和rk代入式(1)，该式可变为

(3)

(4)

将式(4)等比数列求和，化简可得推出σ的表达式为

(5)

式(5)为小散射源RCS阵列合成公式。由该式可知，根据入射电磁波波长，合理地进行小散射源设计，恰当选择散射源数目和阵元间距，可对旋翼结构实现给定RCS特性的无源模拟。

2 原理样机及试验方案

为验证本文所提出的基于小散射源阵列的旋翼增强技术的可行性和有效性，结合国内某型无人直升机旋翼的形状结构特点，设计和研制了一款旋翼增强装置原理样机，制订了试验方案，在微波暗室里开展了实物测量，对所得RCS数据进行了处理，从峰值大小、波峰数目、波峰位置及主瓣宽度4个方面将实际测量结果和与理论仿真结果进行对比分析。

2.1 样机设计

样机包含散射源和结构件两部分。考虑到本次试验采用的旋翼厚度约为21 mm，小散射源最大直径取为18 mm，呈半椭球状，小散射源实物如图2所示。结构件用于固定小散射源的测试姿态，且便于调整阵元数目和阵元间距。结构件采用高透波材料制成，其本身对阵列的散射特性影响可以忽略。旋翼增强装置原理样机实物如图3所示。

图2 小散射源实物图Fig.2 Picture of small scattering sources

图3 旋翼增强装置原理样机实物图Fig.3 Picture of rotor enhancement device prototype

2.2 试验方案

由式(5)可知，当雷达波垂直于阵列面入射时，θ=0°，此时阵列合成RCS可取到最大值：

σmax=σ|θ = 0=N2σ0

(6)

即在单个小散射源RCS一定的情况下，阵列合成RCS的峰值随阵元数目平方递增。

真机的旋翼直径一般超过12 m，经仿真计算在Ka波段大都在1 dBsm量级。在设计模拟方案时，小型无人机旋翼越厚，散射源可物理实现的直径就越大，达到增强指标所需的阵元数目也就越少。根据式(6),若选用-30 dBsm的散射源，32个阵元即可实现旋翼峰值的模拟；若选用-20 dBsm 的散射源，则所需阵元数目大大减少，10个即可满足要求。本文中采用的原理验证机，阵元数目为15个。

根据暗室测试能力及试验目的，制定试验方案如表1所示，部分测试状态见图4。

表1 旋翼增强技术有效性验证方案

图4 试验验证部分测试状态图Fig.4 Partial test status diagram of test verification

3 测试结果

3.1 峰值大小

样机中的散射源在VV极化不同点频测试模式下的RCS分布特性如图5所示。从上到下依次为频率f为20、15、10 GHz所对应的曲线。小散射源RCS频率响应特性非常明显，随频率降低而减小，3个频点下最大值分别约为-18.7、-25.2、-27.5 dBsm；通常0°方位附近较为平坦，一定角度后逐渐向两边递降；3 dB响应角域大都在±40°之间。

Case 2的测试曲线和仿真曲线对比如图6所示。仿真计算峰值约为-1.68 dBsm，实际测量峰值约为-2.84 dBsm，仅相差1.16 dB。就15个-25.2 dBsm的阵元合成精度而言，实测值和计算值吻合较好。从图中可以看出仿真曲线的所有峰值大小一致，而测试曲线的峰值大小从中间向两边依次递减，这是因为仿真时将阵元视为一个各向同性的散射源，可实际情形并非如此，而是随角度从中心向两边递减(见图5)，因而两边的峰值会低于中心峰值。此外，测试曲线的波峰少于仿真曲线，这是由于在3 dB响应角域之外阵元RCS急剧减小引起的。从图5实线表示的f=15 GHz阵元特性曲线可以看出，在图6仿真曲线边缘两个峰的位置，阵元RCS峰值低于-45 dBsm，因此实际测量时无法形成波峰。

图5 小散射源RCS分布特性测试曲线(Case 1)Fig.5 Test curves of RCS distribution characteristic of small scattering source (Case 1)

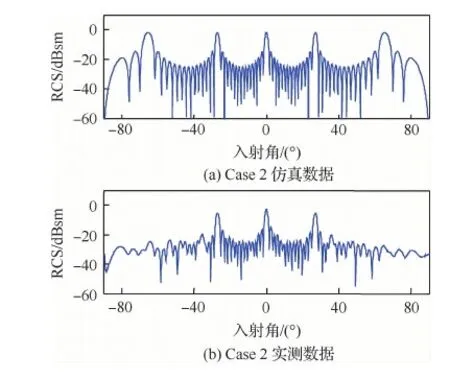
图6 阵列RCS峰值大小特征对比验证曲线(Case 2)Fig.6 Verification curves of peak value characteristics of array RCS (Case 2)

3.2 波峰数目

当sinθ=0 时，由诺必达法则，阵列RCS就可取到最大值σmax。此时

(7)

式中：k虽为整数，但并不能随意取值，这是因为：

(8)

可推出如下不等式：

(9)

因此k的取值为

k=0,±1,±2,…,±[2d/λ]

(10)

式中：[2d/λ]为不大于2d/λ的最大整数。通常把k取值为0，即θ=0°的波峰称之为主瓣，其余波峰则为旁瓣。

显然，阵列RCS的波峰数目M可表示为

(11)

可见，阵列RCS的波峰数目由阵元间距与入射雷达波波长的比值唯一确定，与阵元数目无关。

Case 3的测试曲线和仿真曲线对比如图7所示。显然，实测结果和仿真结果的一致性非常好，RCS分布特性都呈现出3个波峰。同时，在阵元3 dB响应角域之内，波峰之间的次峰数目都是13个，完全吻合。

图7 阵列RCS波峰数目特征对比验证曲线(Case 3)Fig.7 Verification curves of peak number characteristics of array RCS (Case 3)

3.3 波峰位置

由式(7)和式(10)可得，当雷达波从如下角度入射时，阵列RCS可达到峰值：

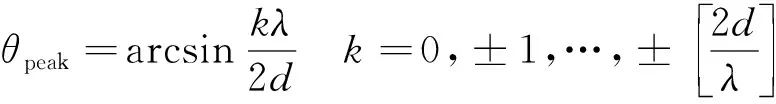
(12)

可见，阵列RCS的波峰位置也是由阵元间距与入射雷达波波长的比值唯一确定，与阵元数目无关。

Case 4的测试曲线和仿真曲线对比如图8所示。仿真数据表明5个波峰的位置从左到右分别

图8 阵列RCS波峰位置特征对比验证曲线(Case 4)Fig.8 Verification curves of peak locations characteristics of array RCS (Case 4)

为-42.99°、-19.93°、0°、19.93°和42.99°；而实测数据中波峰的位置分别为-43°、-20°、0°、19.8°和42.8°，实测时角度取值精度为0.2°，两者差异非常小。

3.4 主瓣宽度

通常而言波束宽度指半功率宽度，但影响波束半功率宽度的因素有很多，除阵元数目、阵元间距、雷达波长等因素之外，小散射源自身的散射特性的方向性也是非常重要的一个方面，因此波束半功率宽度既不好仿真计算，又难以实际测量[24]。鉴于上述原因，从模拟相似度出发，本文中定义主瓣宽度为主瓣左右第一极小值点(零点)之间的角域跨度。

由式(5)可推导出零点位置：

(13)

于是主瓣宽度θbw可表示为

(14)

由此可知，阵列RCS的主瓣宽度由阵元间距、雷达波长、阵元数目三者共同决定。

Case 5的测试曲线和仿真曲线对比如图9(a)所示，图9(b)为将主瓣放大后的情形。仿真曲线主瓣宽度为4.0°，而实测曲线主瓣宽度为3.8°，相差甚微。

图9 阵列RCS主瓣宽度特征对比验证曲线(Case 5)Fig.9 Verification curves of mainlobe beamwidth characteristics of array RCS (Case 5)

4 特性分析

根据国内外已有的研究成果可知，当旋翼桨叶垂直于雷达时，可探测到极为明显的峰值信号，而雷达从其他角度入射时可检测到低水平的反射信号，这一现象被称之为“桨叶反射”，其RCS分布具有强散射、单峰值以及窄角域的特点[7]。下面从以上3个方面对方案的模拟结果进行讨论分析。

4.1 强散射模拟

由式(6)可知，阵列合成RCS的峰值大小取决于阵元数目和单个散射源的RCS。在旋翼RCS峰值大小模拟需求已知，单个散射源RCS实际测得之后，即可确定阵元数目。在实际应用中，考虑到各散射源幅度响应和相位响应的不一致，以及桨叶蒙皮的透波性等因素，需留出部分余量，并通过测试对峰值进行验证，相关内容将在后续工作中展开进一步研究。

4.2 单峰值模拟

这一特征需要通过对小散射源进行角域调制模拟。从图6中可以发现，RCS实测曲线比仿真曲线左右边缘各少了一个波峰。原因在前文已有阐述，是由于这两个波峰的位置(分别为-65.38°和65.38°)超出了散射源的3 dB响应角域范围(约±40°)，因而雷达波从这两个角度入射时，阵元的瞬态回波响应非常小，无法形成波峰。基于这一原理，对小散射源进行角域调制，使其3 dB响应角域进一步减小，一直到小于第一左旁瓣和第一右旁瓣之间的角度间隔，即可实现旋翼单峰值特征的模拟。当然，散射源的3 dB响应角域范围必须大于所需模拟的旋翼RCS峰值的角域宽度。

4.3 窄角域模拟

文献[23]指出，旋翼反射信号的角域宽度约为λ/L，L为旋翼桨叶展向长度。在强散射、单峰值两大特征实现的前提下，根据式(15)，调整阵元间距d，使得阵列合成RCS的主瓣宽度近似等于λ/L，可实现旋翼RCS窄角域特性的有效模拟。实际上，当入射波长λ远远小于阵列长度Nd时，式(14)可进一步化为

(15)

从理论上来说，考虑到阵列沿着展向均匀排布，不考虑桨毂和端部尺寸，阵元的角域宽度与真机旋翼反射信号的角域宽度近似吻合。

5 结 论

针对直升机电磁目标特性模拟需求，本文提出了一种基于小散射源阵列的新型旋翼增强技术，经仿真计算和暗室测试数据对比验证表明：

1) 测试结果与仿真结果吻合较好，充分证明了本方案的可行性和有效性，为直升机目标特性无源模拟提供了新思路。

2) 阵列合成RCS的峰值与阵元数量平方成正比，波峰数目及位置由阵元间距与入射雷达波波长的比值唯一确定，与阵元数目无关，阵列合成RCS的主瓣宽度由阵元间距、雷达波长、阵元数目三者共同决定。

3) 根据直升机桨叶的尺寸、厚度、蒙皮透波率等因素，合理调整散射源的尺寸、RCS特性、排布间距等参数，可有效模拟目标直升机旋翼的强散射、单峰值以及窄角域特性。

在后续工作中，将对改装后旋翼的挥舞特性、扭振模态等直升机旋翼动力学特性以及散射源幅度和相位的一致性对合成效率的影响等因素进行分析，为该新技术的工程应用提供更坚实可靠的技术支撑。