共因失效相关同级叶片系统可靠性分析
李洪伟,陈庆贵,*,徐筱李,洪杰
1.海军航空大学 青岛校区,青岛 266041 2.北京航空航天大学 能源与动力工程学院, 北京 100083
航空发动机叶片结构复杂,在高压、高转速、多载荷的环境下工作,不仅要求其轻质高效,还要求具有长寿命和极高的可靠性、安全性[1]。航空发动机的叶片数量较多,发生故障的次数也较多。据统计,从1975-2002年,某型发动机共发生69起叶片故障[2]。由此可见,叶片的可靠性对于发动机的整机可靠性具有重要影响,有必要结合其特点进行可靠性分析。
航空发动机同级叶片往往具有相同的尺寸、形状、材料、工艺、装配方式等结构、装配特征,同时具有相同的转速和温度等载荷特征。因此,同级轮盘上不同叶片之间一般具有相同的失效模式,且叶片间的可靠度也具有一定的相关性。白斌[3]和张春宜[4]等用极值响应面与蒙特卡罗法对叶盘结构的单扇区以及单个叶片进行了应力、总变形的可靠度分析,但没有考虑叶片之间的相关性。航空发动机采用的经典可靠性分配模型假设各个构件的可靠度是相互独立的,将同级每个叶片可靠度的乘积作为该级叶片的总可靠度[4],这样会导致叶片分配的可靠指标过高,难以指导实际的设计制造。一些学者已注意到具有同一失效模式的多个相同结构的可靠度的综合问题,陆山等[5-6]提出了具有强度相关性的同级叶片系统仅考虑强度失效时的可靠度区间估计方法。谢里阳[7]和王正[8-11]等考虑系统中各零件之间存在的相关性,引入条件概率建立了一种失效模式下考虑相关性的系统可靠性模型。
航空发动机同一个叶片上可以存在多种失效模式,例如低周疲劳断裂、腐蚀、变形等,由于物理上的不可分割,同一个叶片上的不同失效模式之间具有一定的相关性。安伟光等[12]采用概率网络评估(Probabilistic Network Evaluation Technique,PNET)法计算得到考虑失效模式间相关性的桁架结构系统的可靠度,但PNET法在经验缺乏的情况下精度不高。Jimenezrodriguez和Sitar[13]运用蒙特卡罗法计算了多失效模式相关的岩质边坡系统可靠度,但用蒙特卡罗法解决多构件多失效模式的问题时计算效率不高。
本文借鉴上述研究,针对目前方法存在的不足,建立了既考虑构件间相关性,又考虑同一构件内不同失效模式间相关性的多失效模式结构系统可靠性模型,并采用近似数值分析法对航空发动机同级叶片系统进行了可靠性分析。
1 一般失效相关系统可靠性模型
1.1 失效模式间的相关系数
相关系数可以反映2个随机变量之间的相关程度,失效模式i、j的功能函数Zi、Zj可以表示为
(1)
式中:g为失效模式;xi(i=1,2,…,n)表示随机变量。
失效模式的功能函数值Z也是随机变量,它们的相关系数rij为
(2)
式中:
式中:σxk和σxl为xk和xl的标准差;rxkxl为随机变量xk和xl的线性相关系数;P*为验算点;rij为i、j两失效模式间的相关系数。
1.2 近似数值分析法
近似数值分析法采用了条件概率原理,计算简便,精度满足工程要求,可靠度计算公式为
(3)
式中:
P′f1=Pf1
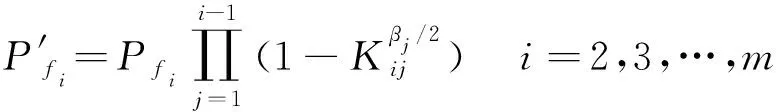
(4)
其中:βj为结构可靠指标;Pfi为失效概率;m为失效模式个数。
(5)
近似数值分析法的计算步骤可归纳为:
1) 确定航空发动机结构系统的主要失效模式。
2) 计算每个主要失效模式的结构可靠指标βj和失效概率Pfi。
3) 评估或者计算各个主要失效模式之间的相关系数。
4) 从大到小排列失效模式的失效概率,使Pf1≥Pf2≥…≥Pfm。
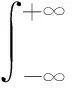
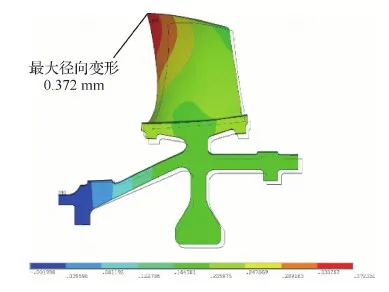
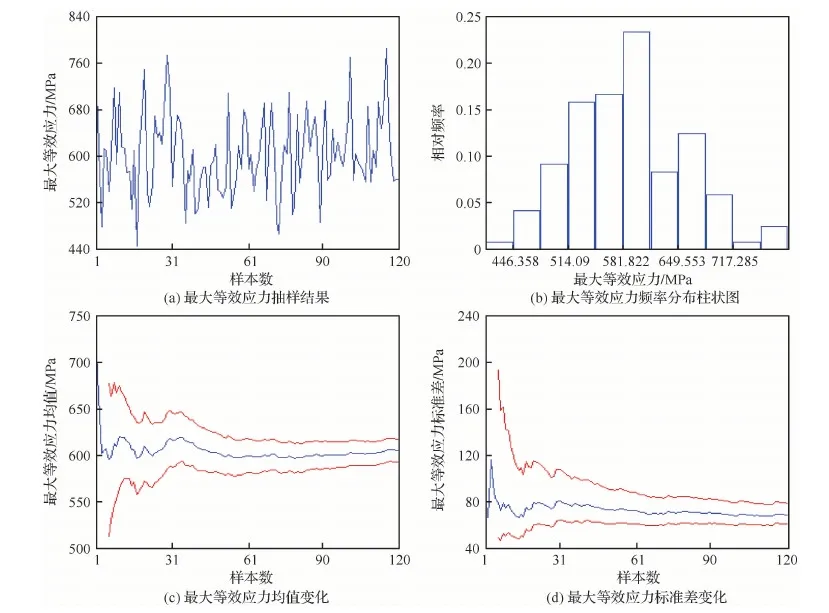
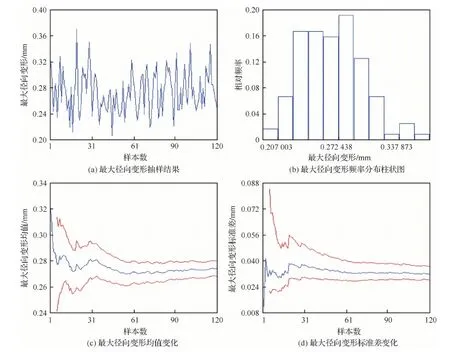
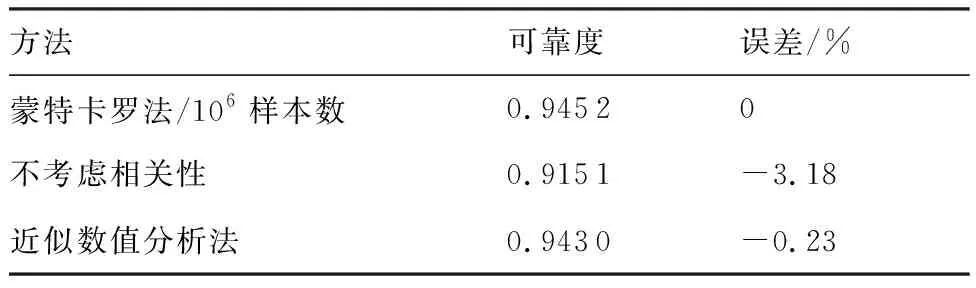
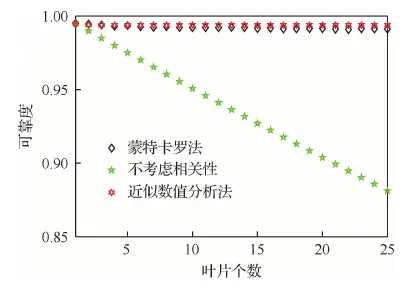
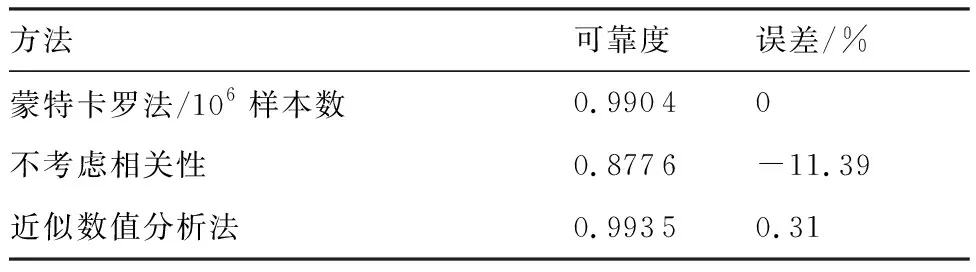
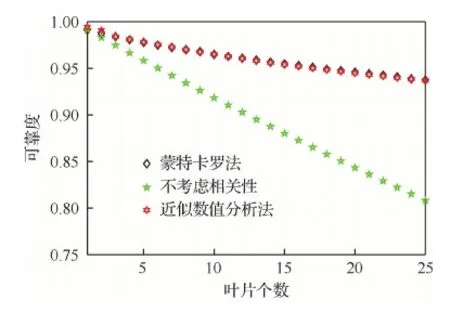
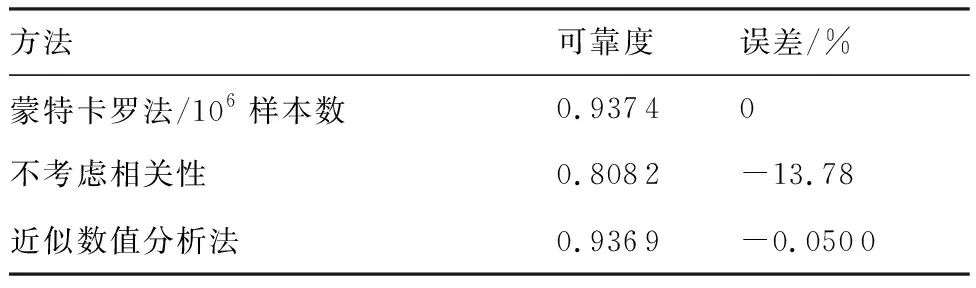
5) 对于每一个i,由式(5)计算每一个j(j 6) 由式(3)计算R。 航空发动机结构系统具有零件个数多、结构周期对称等特点,因此,航空发动机结构系统中的很多失效都是共因失效。针对航空发动机中存在的共因失效相关的情况,在文献[7-11]提出方法的基础上进行扩充改进,建立适应性更广的航空发动机结构系统共因失效相关可靠性模型。 对于具有m个失效模式的结构系统,假设各失效模式都受同一广义载荷(以下简称“载荷”)作用,如果载荷L是定值,那么各失效模式的可靠度都是载荷造成的广义应力小于广义强度的概率。对于失效模式i,其可靠度Ri可以表示为 i=1,2,…,m (6) 式中:m为失效模式的总数;δi为第i个失效模式的广义强度;fδi(δi)为δi的概率密度函数;si(L)为第i个失效模式中由于载荷L所产生的应力。 航空发动机结构系统中不同构件的广义强度有时是相互独立的,例如涡轮的广义强度和压气机的广义强度就是独立的。因此,载荷等于L时,考虑多失效模式共因失效的航空发动机结构系统可靠度为 (7) 式中:Fδi(si(L))为δi的累积分布函数。 设载荷L的概率密度函数是fL(L),由全概率公式可以得到 (8) 式(8)即为考虑共同载荷造成的共因失效相关时,而且广义强度相互独立时,具有多种失效模式的结构系统的可靠性模型,在形式上表现为零部件所受的外载荷L与零部件各失效模式所对应的强度指标δi(i=1,2,…,m)之间的干涉。该方法没有作独立性假设,不需要依赖于零部件各失效模式之间的相关性。 对航空发动机来说,一般失效模式的功能函数会包含超过2个的参数,不仅有强度、载荷参数,还可能有材料、结构等参数,即难以写为式(3)的载荷-强度的简单形式。对于这种情况,可以采用多重积分的思想,设xj(j=1,2,…,n)是载荷、结构、材料参数,δi(i=1,2,…,m)是强度参数,si(x1,x2,…,xn)表示在x1,x2,…,xn作用下的对应失效模式i的应力,则可靠度表示为 (9) 对任意一台航空发动机进行可靠性分析时,需要用到材料参数、几何参数、载荷参数、装配参数,每一次分析都相当于从参数的母体(全部发动机的所有参数集合)中随机抽取子样。对同一参数,假设母体数量较多,参数子样满足独立同分布性质,为简单随机子样。例如,某发动机同级叶片的强度就是简单随机子样。 航空发动机中有很多旋转周期对称结构系统,从统计抽样角度看,一个旋转周期对称结构的对称单元系统与所有旋转周期对称结构的对称单元系统之间的关系就是一组简单随机子样相对于母体的关系,每个对称单元强度的概率密度分布与所有对称单元强度的概率密度分布相同。从结构角度看,旋转周期对称结构每个对称单元上都有相同的危险点,都可能成为实际的失效点。为简化考虑,假设对称单元承受的载荷都是相同的,那么每个旋转周期对称结构中强度最小的对称单元的可靠度就是这个旋转周期对称结构在该载荷下的可靠度。因此,可以用对称单元的强度最小值作为该旋转周期结构的强度。 设旋转周期对称结构系统具有n个对称单元,对称单元强度的概率密度分布函数和累积分布函数分别为fδi(δ)和Fδi(δ)。由上述分析可知,旋转周期对称结构系统强度即为n个对称单元强度的最小顺序统计量,旋转周期对称结构系统强度的累积分布函数可以表示为 (10) 概率密度函数可以表示为 (11) 式(10)和式(11)所示的旋转周期对称结构系统强度概率分布函数中含有对称单元数n,可见对称单元个数对旋转周期对称结构系统的可靠度是有影响的。根据应力-强度干涉模型可以得到旋转对称结构零部件的可靠性模型为 (12) 式中:n为该旋转对称结构系统所具有的对称单元数;fδi(δ)和Fδi(δ)分别为对称单元的强度概率密度分布和累积分布;fs(s)为应力s的概率密度分布。 写成载荷形式为 (13) 式中:si(L)为载荷L作用在对称单元i上的应力;fL(L)为载荷L的概率密度分布。 对于有多个设计参数的情况,设xj(j=1,2,…,l)是载荷、结构、材料参数,δi(i=1,2,…,m)是独立同分布的强度参数,si(x1,x2,…,xl)表示在x1,x2,…,xl作用下的对应失效模式i的应力,则可靠度表示为 [1-Fδi(si(x1,x2,…,xl))]ndxl…dx2dx1 (14) 上述模型在符合条件的情况下是不依赖于相关系数且没有假设误差的,但是只能用于广义强度相互独立的情况。航空发动机中部分失效模式的广义强度是有相关性的,例如同一个构件的静强度和疲劳强度之间是相关的,这种情况可以采用近似数值分析法与上述方法相结合。 特殊地,对于旋转周期对称结构系统,设旋转周期对称结构有n个周期对称结构单元,每个周期对称结构单元都具有k个失效模式,考虑以下情况:同一个周期对称结构单元中的k个失效模式的广义强度之间具有相关性rij(i,j=1,2,…,k),不同周期对称结构单元中的失效模式广义强度之间是独立同分布的。在确定性载荷L作用下,各周期对称结构单元的可靠度不相关,因此结构系统的可靠度为 (15) 式中:R(L)为载荷L为确定值时多失效模式结构系统的可靠度;Rp(L)是载荷L为确定值时单个周期对称结构单元多失效模式的可靠度;P′fi(L)为载荷L为确定值时失效模式i的等效失效概率[14],可以通过式(16)求得 i=2,3,…,m (16) 式中:βi为失效模式i的结构可靠指标;Pfi(L)为载荷L为确定值时失效模式i的失效概率。 设L的概率密度函数为fL(L),根据全概率公式,多失效模式结构系统的可靠度为 (17) 航空发动机同级叶片系统的失效相关性主要体现在2个方面:一是同级不同叶片的同类型失效之间具有相关性,且认为两两叶片间同类型失效模式相关系数相等。例如同级1号叶片和2号叶片的静强度失效之间具有相关性,即:rgagb=rgcgd≠0(a,b,c,d∈[1,N]且a≠b,c≠d),其中,g代表一种失效模式,a、b、c、d代表叶片编号,N为叶片总数,r为失效相关系数。二是同一叶片的不同类型失效之间具有相关性。例如同一叶片静强度失效和变形失效具有相关性,即:rg1g2≠0。g1代表一种失效模式,g2代表另一种失效模式,r为失效相关系数。 某型航空发动机第二级压气机叶盘系统有25个叶片,将其看作由25个对称单元组成的旋转周期对称结构系统进行可靠性分析。 为简化考虑,设随机输入变量有转速ω、密度ρ、弹性模量E、强度极限δ和允许径向变形间隙Δ,随机变量的概率分布特征如表1所示。 表1 压气机叶片随机变量分布特征Table 1 Distribution characteristics of random variables for compressor blades 4.2.1 有限元计算 取叶盘的1/25进行有限元计算,转速、密度、弹性模量都取均值,得到叶片等效应力分布如图1 所示,最大等效应力位于叶片根部,为763.2 MPa,小于强度极限1 000 MPa。径向变形分布如图2所示,最大径向变形位于叶片外缘,为0.372 mm,没有超过允许径向变形值。 图1 涡轮叶片等效应力分布Fig.1 Equivalent stress distribution of turbine blades 图2 涡轮叶片径向变形分布Fig.2 Radial deformation distribution of turbine blades 4.2.2 最大等效应力响应面 当转速、密度、弹性模量服从表1中所示的正态分布且彼此独立时,在ANSYS中进行120次抽样计算,叶片根部最大应力值抽样结果,均值、标准差随抽样次数的变化结果如图3所示,结果显示已基本收敛。 可以得到叶片根部最大等效应力的含交叉项二次响应面函数为 图3 叶片最大等效应力ANSYS仿真结果Fig.3 ANSYS simulation results of blades’ maximum equivalent stress ρs=4.4×109×ρ-20 ωs=5.1×10-3×ω-20 Es=2×10-4×E-20 式中:ρs、ωs、Es分别为归一化的密度、转速、弹性模量。叶片根部最大等效应力σmax为 (18) 式中:a1=30,a2=60,a3=-0.006,a4=0.001,a5=0.1,a6=0.003,a7=0.3, a8=-0.03,a9=0.02。 4.2.3 最大径向变形响应面 当转速、密度、弹性模量服从表1中所示的正态分布且彼此独立时,在ANSYS中进行80次抽样计算,叶片外缘最大径向变形值抽样结果,均值、标准差随抽样次数的变化如图4所示,结果显示已基本收敛。 可以得到叶片外缘最大径向变形的含交叉项二次响应面函数为 ρs=4.4×109×ρ-20 ωs=5.1×10-3×ω-20 Es=2.0×10-4×E-20 (19) 式中:Uxmax为叶片外缘最大径向变形值;b1=0.3,b2=0.01,b3=0.03,b4=-0.01,b5=-1×10-5,b6=6×10-4,b7=7×10-4,b8=1×10-3,b9=-7×10-4。 图4 叶片最大径向变形ANSYS仿真结果Fig.4 ANSYS simulation results of blades’ maximum radial deformation 4.3.1 叶片静强度不足失效 要计算单一叶片静强度不足失效的可靠度,可以直接用ANSYS进行蒙特卡罗法仿真抽样,由于计算量比较大,本文采用由ANSYS得到的叶片根部最大等效应力响应函数,基于MATLAB编程进行可靠度计算。设该级压气机25 个叶片的转速是相等的,密度、弹性模量、强度服从各自的母体分布,而且由简单字样的概念可知,25 个叶片各自的密度、弹性模量、强度可以看作独立同分布的。由于转速相等,因此25 个叶片静强度失效之间是相关的,采用考虑相关性的蒙特卡罗法、不考虑相关性的可靠度计算方法以及近似数值分析法进行可靠度计算。不同叶片数目下叶片静强度不足失效可靠度的计算结果如图5所示,3种方法计算的25 个叶片静强度不足失效可靠度的对比如表2所示。 可见,如果不考虑叶片静强度失效之间的相关性,结构系统可靠度将过于保守;近似数值分析法的可靠度也是偏保守的,但是与蒙特卡罗法相比误差很小。两叶片静强度失效之间的相关系数为0.43。 图5 不同叶片数目下的静强度不足失效可靠度Fig.5 Reliability of insufficient static strength failure with different numbers of blade 表2 3种方法计算的静强度不足失效可靠度比较 Table 2 Reliability comparison of relative error for insufficient static strength failure with three methods 方法可靠度误差/%蒙特卡罗法/106样本数0.94520不考虑相关性0.9151-3.18近似数值分析法0.9430-0.23 4.3.2 叶片外缘变形碰摩失效 设该级压气机25 个叶片的转速、允许径向变形间隙是相等的,密度、弹性模量各自服从各自的母体分布,而且由简单字样的概念可知,25个叶片各自的密度、弹性模量可以看作独立同分布的。由于转速、允许径向变形间隙相等,因此25 个叶片静强度失效之间是相关的,采用考虑相关性的蒙特卡罗法、不考虑相关性的可靠度计算方法以及近似数值分析法进行可靠度计算。不同叶片数目下叶片外缘变形碰摩失效可靠度的计算结果如图6所示。3种方法计算的25个叶片外缘变形碰摩失效可靠度的对比结果如表3所示。 可见,如果不考虑叶片径向变形超过允许间隙失效之间的相关性,结构系统可靠度将过于保守;近似数值分析法与蒙特卡罗法相比误差很小。由于两叶片间参数相关程度较大,包含了2个完全相关的参数,因此失效模式之间的相关性也较大,相关系数为0.990 8。 图6 不同叶片数目下的叶片外缘变形碰摩失效可靠度Fig.6 Reliability of blade outer margin deformation rub failure with different numbers of blade 表3 3种方法计算的叶片外缘变形碰摩失效可靠度比较 Table 3 Reliability comparison of relative error for blade outer margin deformation rub failure with three methods 方法可靠度误差/%蒙特卡罗法/106样本数0.99040不考虑相关性0.8776-11.39近似数值分析法0.99350.31 4.3.3 考虑两种失效模式 设该级压气机25 个叶片的转速、允许径向变形间隙是相等的,密度、弹性模量、强度各自服从各自的母体分布,而且由简单子样的概念可知,25个 叶片各自的密度、弹性模量、强度可以看作独立同分布的。由于转速、允许径向变形间隙相等,因此25 个叶片静强度不足失效、叶片外缘径向变形碰摩失效之间是相关的,采用考虑相关性的蒙特卡罗法、不考虑相关性的可靠度计算方法以及近似数值分析法进行可靠度计算。不同叶片数目下考虑叶片静强度不足失效和叶片外缘变形碰摩失效时间的可靠度计算结果如图7所示。3种方法计算的25个叶片静强度不足失效和叶片外缘变形碰摩失效相关的可靠度对比结果如表4所示。 图7 不同叶片数目下考虑两种失效模式的可靠度Fig.7 Reliability of two failure modes with different numbers of blade 表4 3种方法计算的两种失效模式相关时的可靠度比较 Table 4 Reliability comparison of relative error for two relative failure modes with three methods 方法可靠度误差/%蒙特卡罗法/106样本数0.93740不考虑相关性0.8082-13.78近似数值分析法0.9369-0.0500 可见,如果不考虑叶片静强度不足失效、叶片径向变形碰摩失效之间的相关性,结构系统可靠度将过于保守;近似数值分析法虽然计算过程略复杂,但是与蒙特卡罗法相比误差较小,仅为-0.05%。 本文研究建立了航空发动机同级叶片共因失效相关可靠性模型,并采用蒙特卡罗法、不考虑相关性的计算方法、近似数值分析法对某型航空发动机的压气机叶盘系统进行了可靠度计算。结果表明,由于叶片间的转速、叶片间最大允许径向变形间隙均存在相关性,随着叶片数量的增多,叶片静强度不足失效可靠度、叶片外缘变形碰摩失效可靠度、考虑叶片静强度不足失效和叶片外缘变形碰摩失效时的可靠度均有所下降。如果不考虑叶片的相关性,得到的可靠度过于保守;考虑叶片间的相关性时,近似数值分析法得到的可靠度与蒙特卡罗法计算的可靠度相比误差较小且能大大减少计算量。2 共因失效相关系统可靠性模型
2.1 广义强度相互独立
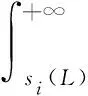

2.2 广义强度独立同分布

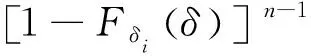






2.3 旋转周期对称结构系统广义强度相关
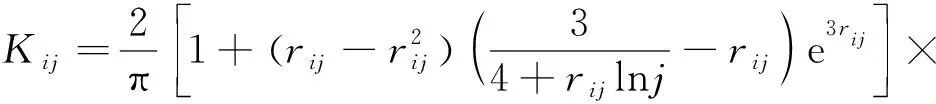

3 同级叶片系统的失效相关性
4 多失效模式同级叶片系统可靠性
4.1 结构分析

4.2 失效分析

4.3 可靠度计算

5 结 论

