基于主成分回归算法的城市客流聚集风险预测

王聚全， 王 伟， 马慧民， 杨 博， 杜 渂

1.迪爱斯信息技术股份有限公司，上海200032

2.电信科学技术第一研究所有限公司，上海200032

3.上海市公安局科技处，上海200042

4.上海市北高新股份有限公司，上海200436

伴随中国经济的腾飞，大型活动逐渐成为促进文化交流和经济繁荣发展的重要载体.诸如上海、北京等规模较大城市，各种大型活动（如节假日欢庆、体育赛事等）的规模和数量与日俱增，随之引发的各种群体性安全问题层出不穷.据中国社科院公布的《社会蓝皮书》数据显示，中国发生的群体性事件从1993年至2005年约增加10 倍，且近几年依然呈现上升趋势[1-2]，尤其是2014年元旦跨年夜发生在上海外滩的踩踏事件再一次给政府应急管理敲响了警钟.

对以往发生的群体性事件进行分析后不难发现，客流密度过大、过度拥挤是事故发生的根本原因[3-4].在大城市，移动网络基本实现了全覆盖，且手机的人群使用量也达到了较高水平[5].因此，如何有效利用现有数据预测客流量的变化情况已逐渐成为业界的重点研究方向，目前客流预测方法大致可分为两类：

一类是基于时间序列的模型预测法[6-7]，代表算法有差分自回归移动平均（autoregressive integrated moving average, ARIMA）模型.该类算法具有模型简单、不需要借助输入变量的优点，但不能捕获非线性关系且有输入数据平稳或差分后平稳的要求.

另一类是基于降维的模型预测法[8]，代表算法有主成分分析（principal component analysis, PCA）法.该类算法的优点是在损失较少的情况下能从众多信息中抽取关键信息，缺点是需要保证主成分因子符号为非负.

综合以上两类算法的优缺点以及通常利用运营商提供的手机用户数据这两方面因素，本文采用主成分分析、回归分析和最小二乘法相结合的数学模型对特定区域的客流聚集人数和趋势进行预判，与ARIMA 算法相比在预测准确度方面有较大提升.

1 算法模型理论

1.1 ARIMA 模型

时间序列的分析模型包括以下几种：自回归[9]（auto-regressive,AR）、移动平均[10]（moving average, MA）、自回归移动平均[11]（auto-regressive moving average, ARMA）、ARIMA 等模型，其中ARIMA 模型作为近年来的最新研究成果，受到了工商界和学术界的广泛关注，其核心公式为

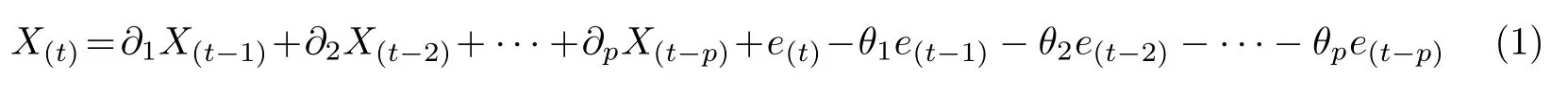
式中，∂[.]表示AR 的系数，e[.]表示MA的系数.ARIMA 模型要求输入的时间序列是平稳时间序列或者经过差分后的平稳时间序列，检验时间序列是否平稳的技术手段是使用时间序列的自相关系数[13]（autocorrelation function, ACF）和偏自相关系数[14]（partial autocorrelation function, PACF）.在参数估计阶段，依据赤池信息准则[15]（Akaike information criterion,AIC）和贝叶斯信息准则[16]（Bayesian information criterion, BIC）确定最优阶数.

1.2 多重共线性

多重共线性的产生是因为模型中自变量之间存在较高程度的相关性，所以自变量之间通常可以相互线性表出，即存在一组不全为0 的系数c0,c1,c2,··· ,cn，使得自变量在几何平面上几乎可以重叠成一条直线[17]，其计算公式为

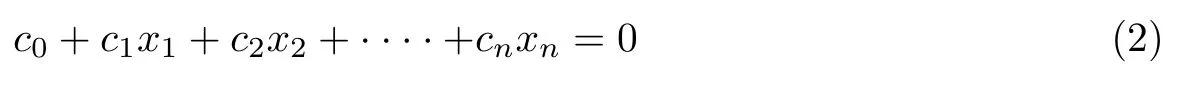
多重共线性越严重，以最小二乘法估计的参数方差就会不断增加，最终导致回归方程的稳健性[18]下降、个别自变量的显著性关系不明显等结果.目前，诊断多重共线性问题方面最常用的指标为容忍度（tolerance）T 和方差膨胀因子（variance inflation factor）Vi.两者之间互为倒数，记xi的方差膨胀因子为Vi，其计算公式为

一旦诊断出模型存在多重共线性，就要想办法解决该问题.近几年，很多学者对该领域进行了大量的研究，在一定程度上缓解了共线性问题带来的预警准确度不高的问题.为进一步提升预警准确程度，本文选择主成分分析法解决以上问题.

1.3 主成分分析

主成分分析是将多种相关性较高的数据转换为少数几个综合指标，从而达到降维的目的.转换后的指标为原始指标的线性组合，且转换后的指标数远少于转换前的指标数，此时也能保留原始数据的绝大部分信息.该过程[19]包括以下内容：

假设原始数据包含的样本量为n，每个样本有p 个属性，则原始数据构成了一个n×p 维的矩阵，具体公式为

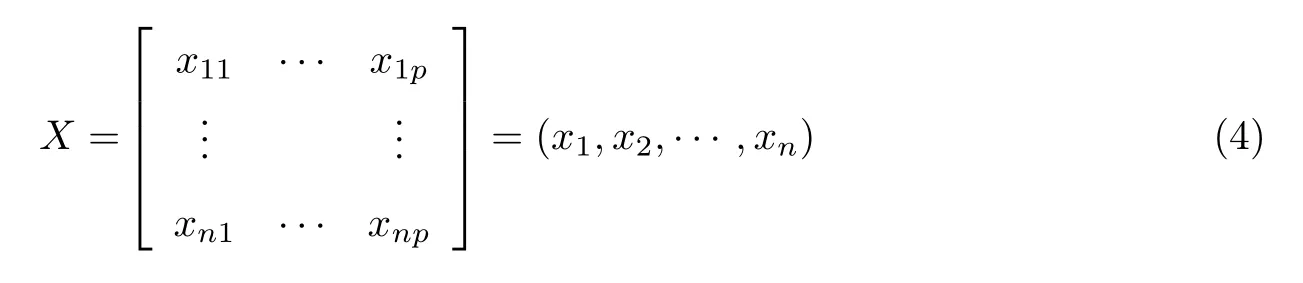
数据众多属性之间的单位和数量级通常存在差异，为了进一步分析研究，应先根据式(5)进行数据标准化变换

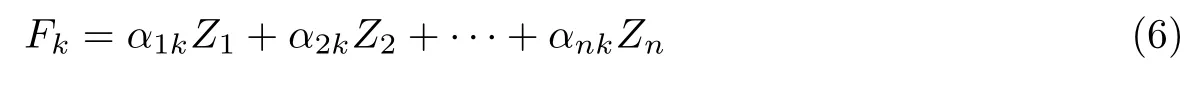
特征值越大对应的方差贡献率越大，于是通过累计方差贡献率来确定最佳的主成分数目.通常选取累计方差贡献率达到80%的前n 个线性组合作为主成分[20]，其计算公式为

1.4 主成分回归

假设随机变量y 与主成分F1,F2,··· ,FP的线性回归模型为[21]

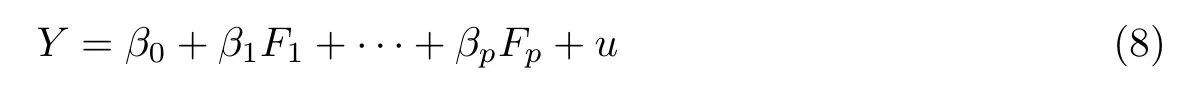
式中，β0为回归函数，常数项βp（i=1, 2,···, p）为自变量回归系数，u 为随机干扰项.将式(8)进行转化后可得其矩阵形式为

根据最小二乘法对方程进行偏导数极值求解，得到未知参数的最小二乘估计值为

2 算法模型构建

在较大城市，移动网络目前几乎实现了全网覆盖，且手机的人群使用量也达到了较高水平，手机信令数据已经成为城市客流聚集风险预测的一种常用数据.运营商网络具有以下两点自身特性：1）运营商网络覆盖范围和实际区域无法完全匹配，且误差范围不稳定；2）某些区域存在基站同时覆盖、信号漂移和干扰等因素.因此，运营商的手机信令数据往往与该区域的真实客流人数有较大差异，不能真实反映该区域的客流聚集程度.

本文从上海市内客流密集的公共场所中选择某区域作为研究对象，分析该区域运营商提供的手机用户数据（该数据为经过脱敏处理后的统计数据而非个体数据.），选择算法所需滞留用户人数X1、滞留用户7 天平均人数X2、新进入用户人数X3、新进入用户7 天平均人数X4、离开用户人数X5、离开用户7 天平均人数X6字段，对所选字段数据进行预处理后得到用户数分布及变化情况如图1 所示.

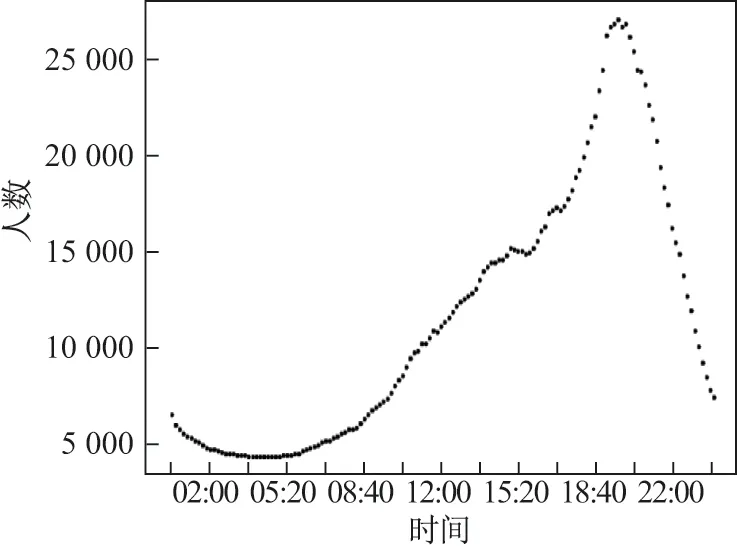
图1 手机用户数分布图Figure 1 Distribution of mobilephone users

2.1 ARIMA 模型参数选择

模型预测前需要对输入的时间序列进行平稳性检验.观察图1 可知该时间序列不平稳，于是对时间序列一阶进行差分，得到自相关系数和偏自相关系数如图2 和3 所示.

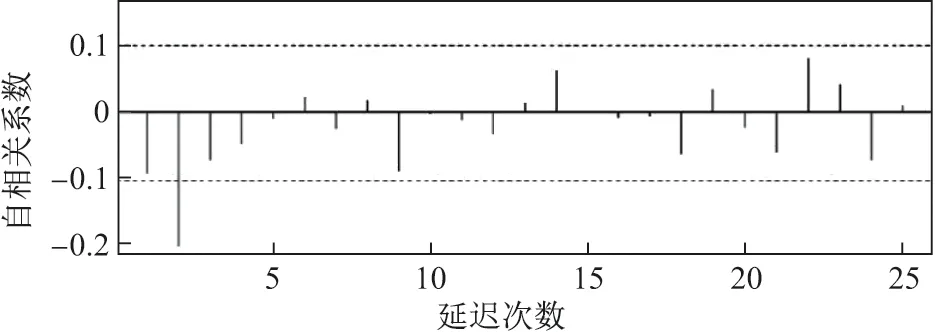
图2 自相关系数分布图Figure 2 Distribution of autocorrelation

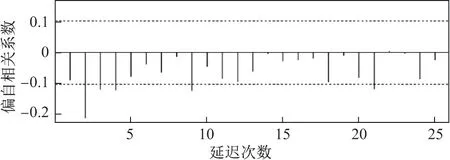
图3 偏自相关系数分布图Figure 3 Distribution of partial autocorrelation

从图2 和3 中可以看出自相关图和偏自相关图二阶拖尾，依据AIC 和BIC 最小的原则可知ARIMA（2,1,2）为最优模型.

模型参数确定后就可以检验其残差分布，合理的模型残差分布应该符合均数为0 的正太分布.本文绘制如图4 所示的残差分布图，可见本文模型的残差分布接近均值为0 的正态分布，符合作为对比实验的条件.

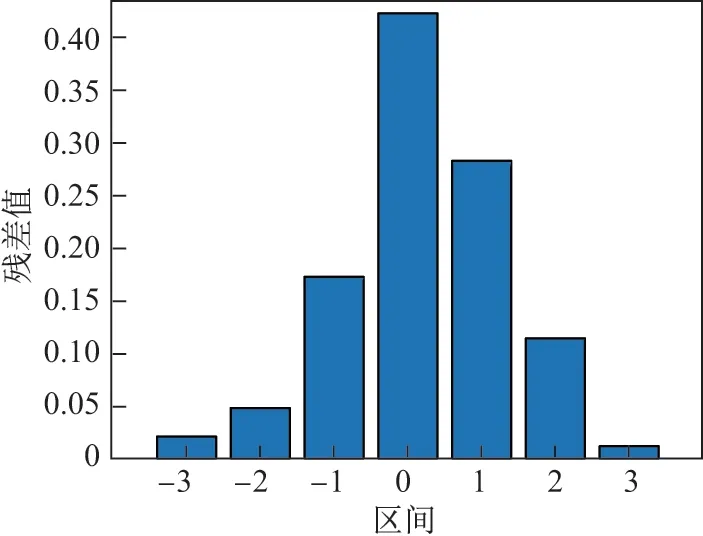
图4 残差分布图Figure 4 Residual distribution

2.2 相关性分析与共线性诊断

分析运营商提供的手机用户数据，得到数据之间的相关系数、容忍度和方差膨胀因子如表1 所示.相关系数矩阵表反映出数据之间的相关性非常高，除了X1和X2为0.88 之外，其余两两之间均超过了0.90，为防止后续建模中出现较为严重的多重共线性，需要诊断变量间的共线性.从表1 的计算结果中可以看出：除了变量X1和X2外，其他变量的容忍度T 均接近于0，方差膨胀因子则较大，X1的膨胀因子最小，但也超过了10.因此，根据容忍度[22]T 和方差膨胀因子[23]Vi这2 个指标数值可以得出变量之间具有较严重共线性的结论.

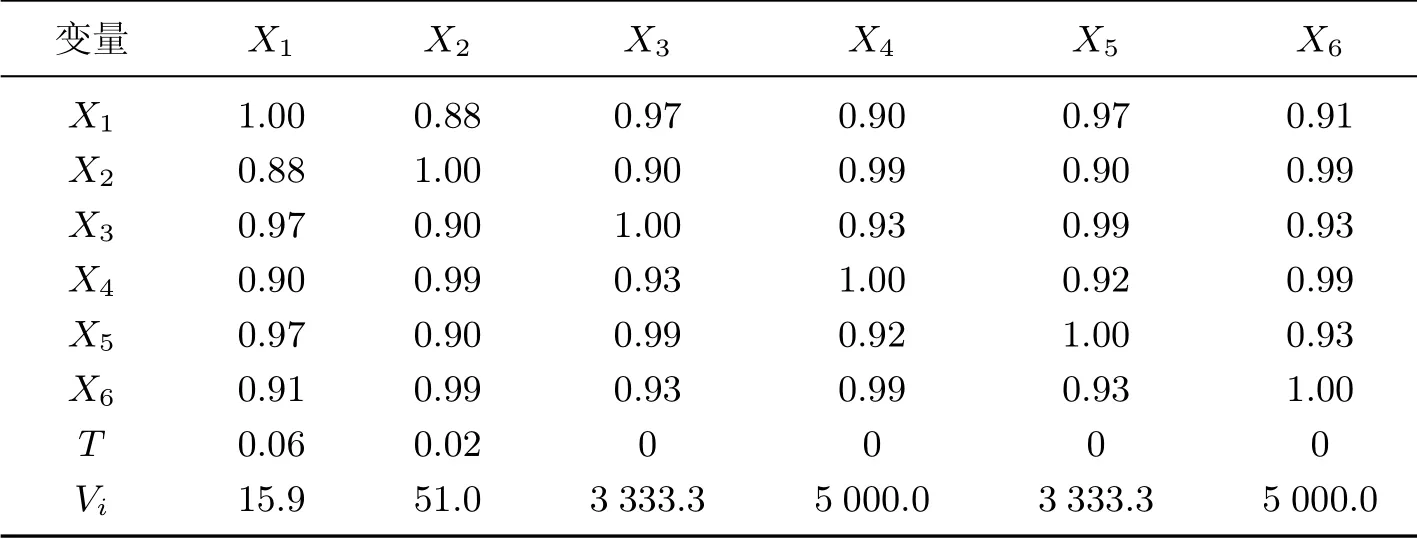
表1 相关系数矩阵及共线性诊断Table 1 Correlation coefficient matrix and colinearity diagnosis

2.3 主成分回归

本文在式（9）中加入结构风险最小化参数，并结合噪声和随机参考项提出了以下训练模型：

该训练模型保留了主成分的回归优势，同时简化了模型的复杂度，提升了模型的泛化率，进一步加速了模型的运行效率.

通过相关矩阵和特征值得出主成分碎石图，如图5 所示.从图5 中可以看出：主成分1 和2 之间的拐角比较大，过渡非常陡峭，而其余主成分之间的过渡则比较平缓.从数值来看，相关矩阵的最大特征值约为6.0，第2 大特征值则小于1，而最小特征值接近于0，故从主成分碎石图可以初步判定本文只需取一个主成分.

通过相关矩阵进一步进行主成分分析，得到如表2 所示的结果，第1 主成分的贡献率已经达到94.98%，第2 主成分的贡献率为4.02%，第3 主成分的贡献率已经小于1%.从方差累计贡献率来看，第1 主成分的累计贡献率已经达到了94.98%，即已经可以解释各类原始数据总贡献率的94.98%，故本文可以只取第1 主成分，因为第1 主成分能反映原始变量接近95%的信息.主成分表达式为

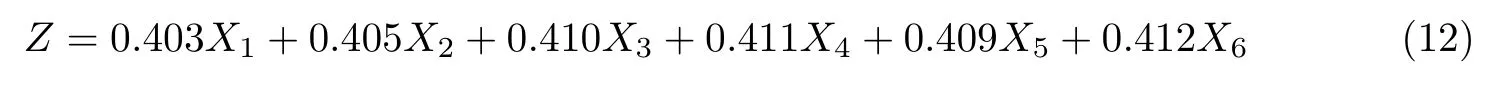
本文先将原始数据进行多重共线性诊断和主成分分析，再把提取出来的主成分与对应时刻的真实客流数据进行比对，通过逐步回归拟合最终得出最优的回归表达式结果如表3 所示.调整后的可决系数高达99.15%，说明整个模型拟合效果较好.主成分的一次项、二次项、三次项估计系数显然都能通过方程参数t 检验，说明主成分的一次项、二次项、三次项均对因变量起重要作用.模型拟合的p 值远小于0.01，显然也能通过F 检验，故主成分回归方程为

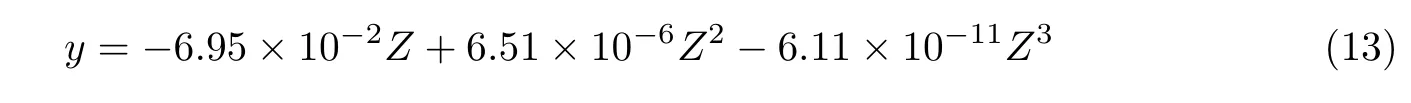
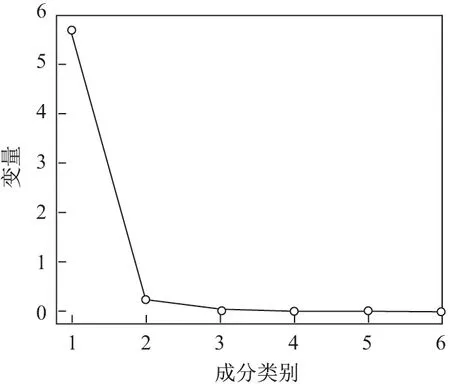
图5 主成分碎石图Figure 5 Principal component lithogram

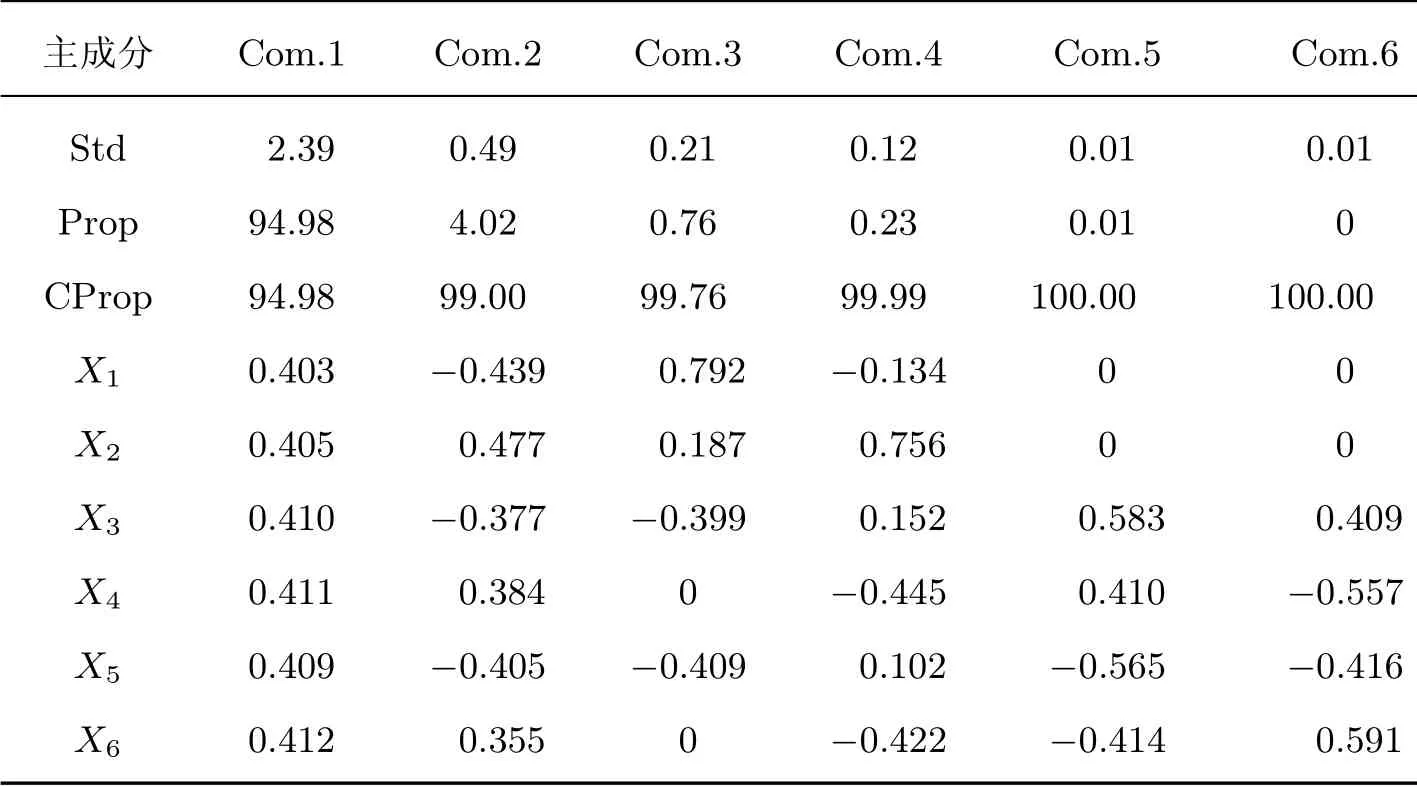
表2 主成分分析Table 2 Principal component analysis

表3 主成分回归结果Table 3 Result of principal component regression

根据表3 的检验结果，预判定式（12）中最高阶数为3 阶，且3 阶判定系数值高达99.2%，调整后的可决系数高达99.15%.判定系数和可决系数值较高，从侧面反映了已定参数阶数的可信度.又因为模型拟合的p 值为2.2×10−6，远小于0.01，所以可确定主成分回归方程定位3 阶，系数值为表3 中Estimate 列对应值，具体如式（13）所示.

3 预测效果评估及对比

3.1 实验数据

实验数据来源于运营商，数据采集开始阶段为2015年9 月至今，每条数据间隔10 min，数据总量截止到实验开始阶段为40×30×24×6 条.数据字段分别为区域名称（编号）、时间戳、用户数（区域内人数）、漫入数、漫出数5 个字段.本文截取了某区域的数据样例展示，如表4 所示.

表4 中区域名是指每个区域的代号，时间指数据采集的具体时间点，用户数为当前基站监测到的固定区域内的人数，漫入数为当前基站监测到新加入用户的数量，漫出数为当前基站监测到的从当前基站流失人员的数量.

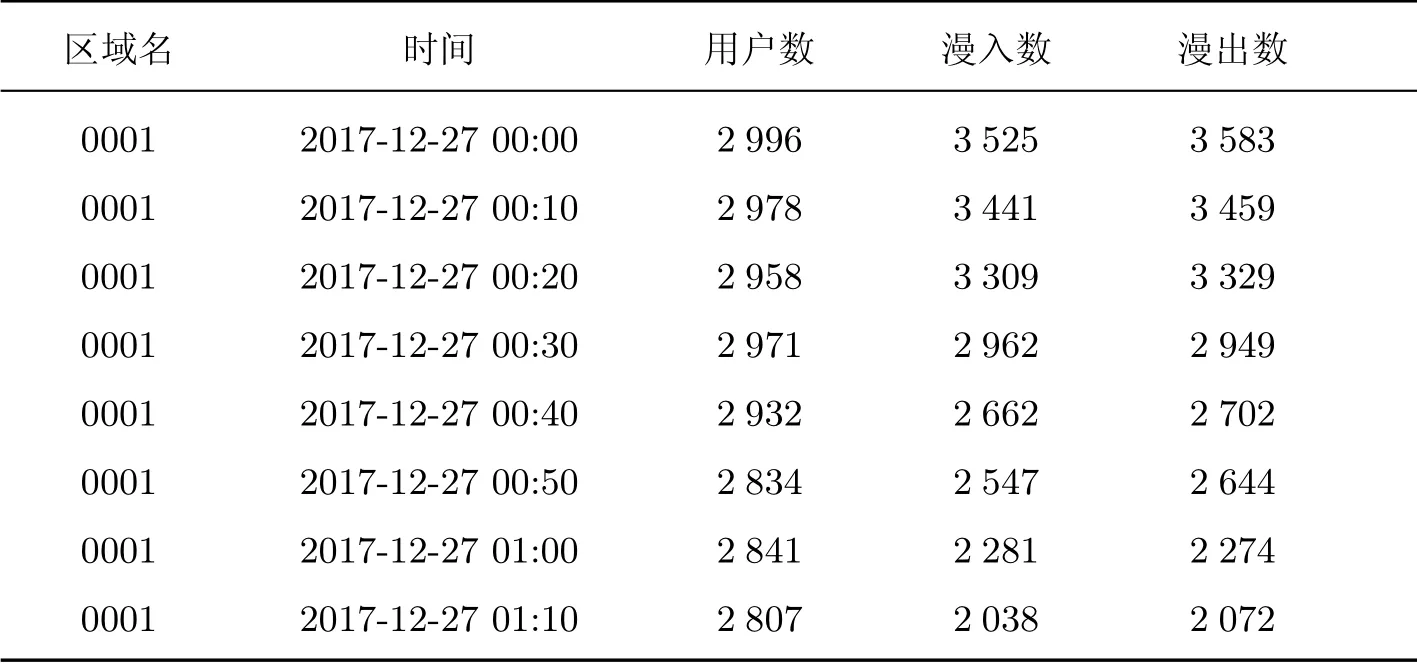
表4 某区域数据Table 4 Area data

3.2 参考指标和误差分布等级

将原始数据代入主成分回归方程可得预测值，再将预测值与相应真实值进行对比，所得结果如图6 和7 所示.预测值与真实值的最小误差回归PCA 为0.67%，平均误差为25.1%，误差中位数为7.79%，与ARIMA 模型相比平均误差中位数明显降低了.个别或少数奇异点的存在导致误差平均值和误差中位数值相差较大，其平均值不能充分反映误差的整体情况，故应以中位数为参考指标.

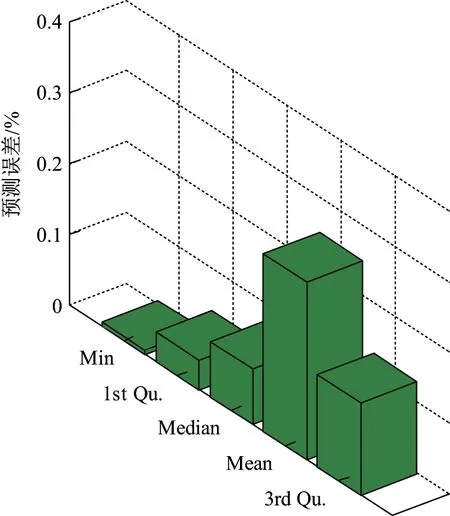
图6 PCA 预测误差分布Figure 6 Distribution of PCA prediction error

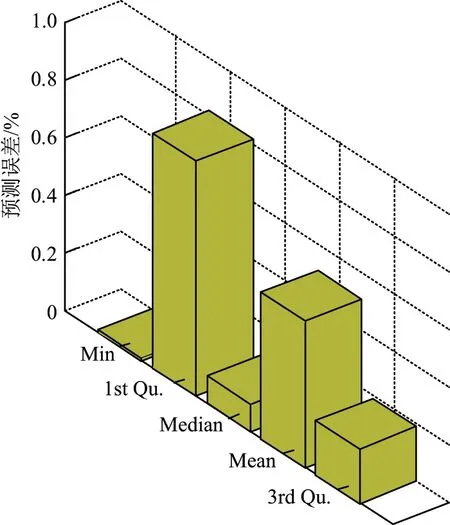
图7 ARIMA 预测误差分布Figure 7 Distribution of ARIMA prediction error

根据图6 和7 将误差范围进行分类，定义误差范围低于10%的数量为1 级，定义误差范围在10%∼20%之间的数量为2 级，定义误差范围在20%∼30%之间的数量为3 级，定义误差范围高于30%的数量为4 级.根据以上4 个等级划分，针对回归PCA 和ARIMA 分别画出预测误差分布图，如图8 所示.回归PCA 的误差范围在10%以内的数量达到了进行预测总数量的62%，误差范围超过30%的数量仅为总数的9%；ARIMA 的误差范围在10%以内的数量仅为34%，误差超过30%的数量为15%，与回归PCA 相比劣势较为明显，可见主成分回归模型的整体预测效果较为理想.

3.3 实验对比

为说明本文算法的可行性和高效性，本文设计了与ARIMA 算法的对比试验，对比效果如图9 所示.

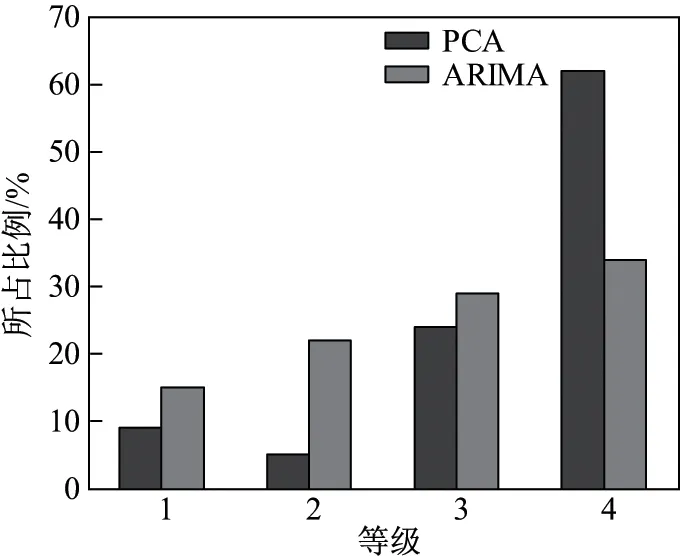
图8 预测误差级别分布Figure 8 Distribution of prediction error level

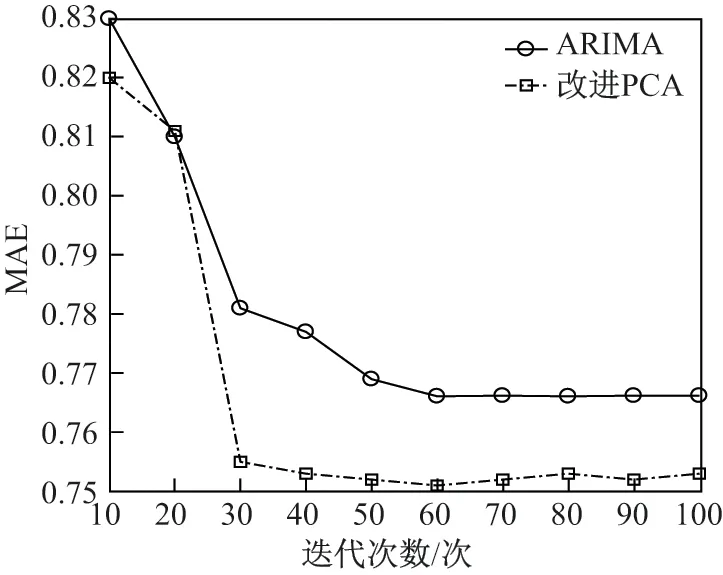
图9 算法对比图Figure 9 Algorithm comparison diagram

从图9 中可以看出，本文算法在整体的预测准确度方面与ARIMA 算法相比差距较小，在效率运行方面如表5 所示.随着迭代次数的增多，改进PCA 算法的准确度得到了提升，同时其运行效率呈高斯分布，即呈现中间高两头低的趋势，原因如下：随着迭代次数的增多，模型复杂度逐步提升，模型训练效果更佳，泛化效果更好.然而，在复杂度提升的同时运行效率略有降低，实验结果符合预期.

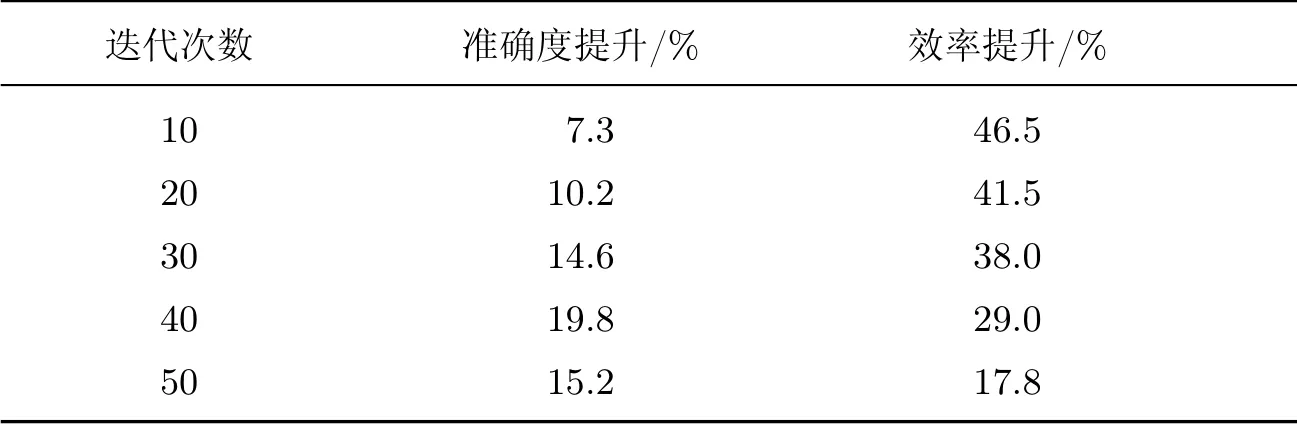
表5 运行效率对比Table 5 Comparison of operating efficiency

4 结 语

本文从运营商提供的手机用户数据出发，对每个维度潜在的特征和规律进行分析和挖掘，发现各个维度之间存在较高共线性，若直接进行回归分析则会使预测结果受到质疑.因此，借助主成分分析具有将多变量简化为少数不相关变量的优点，有效克服了各个维度的共线性问题，降低了算法的复杂度，同时与ARIMA 算法相比预测准确度提升较为明显.从该模型的分析结果中可以看出：因为充分考虑了运营商手机用户数据的各个维度，所以模型的预测精度比较理想，可以为城市的有效管理、客流聚集风险的管控等提供有效的数据支撑.