基于随机时延的多无人机编队控制方法

季 蕾， 樊春霞

南京邮电大学自动化学院，南京210023

现今无人机技术已用于商业、科研和军事等多个领域，无人机的编队运动也成为一个热门的研究课题.在对生物系统的观察过程中，科学家发现了编队运动远优于个体运动，比如大雁组成人字形梯队飞行可以减少阻力，鱼群通过编队也能提高游泳和捕食的效率.因此，无人机的编队运动相对于个体飞行运动而言拥有更高的效率、更强的稳定性和鲁棒性，有利于执行高强度的任务，例如灾情监测、搜索救援等.编队控制是在无人机进行编队运动时保持或改变机组成员队形的控制技术，而现代嵌入式系统技术、网络技术和控制技术为无人机的编队控制提供了许多便捷的方案[1-2].

无人机编队控制方法分为下列几类：1）Leader-follower 法，由编队中的某些特定无人机作为leader，其余的无人机作为follower 跟随leader 运动[3]；2）基于行为法，预设每一架无人机的行为，即飞行速度、运动轨迹等，并基于控制输入的加权平均为每一个行为设计单独的控制输入[4]；3）虚拟结构法，将整个无人机编队看成一个单一的虚拟主体，根据其动力学方程为每一架无人机设计合适的参考轨迹[5]；4）图论法，构造无人机编队拓扑图，以节点表示单架无人机，以边表示无人机间的拓扑结构，即通信关系、控制连接等[6]；5）一致性法，无人机通过与相邻无人机的信息交互更新自身状态，最终达到所有无人机状态一致的目的[7].这些方法各有利弊，在无人机编队控制领域都有应用.

多无人机编队控制的关键就是保证通信交互，但实际上受到恶劣天气、电磁干扰、通信堵塞等原因的干扰，无人机之间的交互信息在通信过程中必定存在时延.文献[8-9]研究了考虑通信时延时变时多无人机系统的一致性问题，提出了分布式动态输出反馈控制器.文献[10-11]在兼顾随机时延的基础上研究了以二阶积分模型描述的多无人机系统的一致性问题.文献[8-11]虽然将无人机的编队飞行建模成质点的运动，但没有考虑无人机自身的非线性，因此其应用范围受到了限制.

本文以垂直起降无人机为研究对象，根据其特性建立非线性动力学模型，利用随机变量描述通信时延的发生，使得无人机组达到预设的编队目标并且保持悬停状态.首先建立垂直起降无人机的动力学模型，设计中间控制输入，利用提取算法推导出无人机的推力和目标姿态.然后以推力作为无人机平移子系统的输入，同时将设计力矩作为无人机旋转子系统的输入，从而实现对目标姿态的跟踪，达到最终编队目标；接着构造Lyapunov-Krasovskii 泛函，推导出保持无人机编队同步的时延相关性条件；最后利用Matlab 进行仿真，验证推导结果的正确性.

1 基础知识

1.1 本文所用物理量的定义

在本文中，R 表示实数集，Rn表示欧氏n 维空间，向量Rp表示p 维列向量，矩阵Rp×q表示p×q 矩阵.In表示n 维单位矩阵.向量x 的时间导数表示为即同样d2x/dt2.

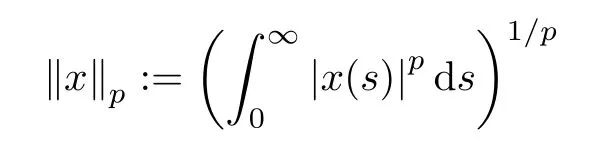
本文所有函数中与时间相关的自变量直接省略(x ↔x(t))，但是带有时延的自变量是不可省略的，如x(t −τ)含有时延τ，故不可省略.当积分项内函数的自变量与微分变量相同时，函数的自变量直接省略函数在无穷处的极限可以表示为

本文以加权图描述无人机组内成员之间的信息交换.加权图G 由三元组(N,γ,K)构成，其中N ={1,··· ,n}是无人机节点的集合，γ 是成对无人机节点的集合（称为边），K =[kij]∈Rn×n是加权邻接矩阵.边(i,j) ∈γ 表示第i 架无人机接收到来自第j 架无人机的信息.加权邻接矩阵定义如下：kii= 0；当(i,j) ∈γ 时，kij> 0；反之，当(i,j)γ 时，kij= 0.本文中系统通信是双向互连的，即G 是无向的，γ 中节点对是无序的，即(i,j)∈γ ↔(j,i)∈γ，K 是对称的，即kij=kji.

本文用单位四元数将无人机飞行姿态的方式定义为

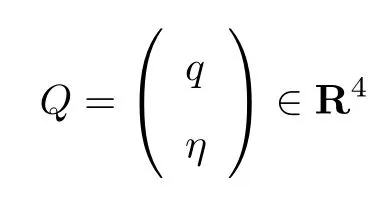
式中，q ∈R3、η ∈R 分别表示单位四元数的向量和标量部分，q = (q1,q2,q3)T；Q 为单位四元数集合，可定义为

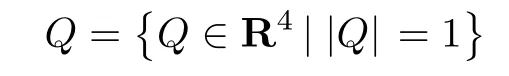
1.2 所用引理

引理1[12]如果

引理2[13]令x(t)为微分方程的一个解，其中a(t)为一致连续函数.如果当t →∞时，x(t)→c，b(t)→0，c 为常数，则当t →∞时，

引理3[13]考虑二阶系统

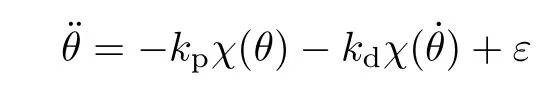
式中，kp和kd均为正标量增益；饱和函数χ(θ)=(σ(θ1),σ(θ2),σ(θ3))T∈R3，θ =(θ1,θ2,θ3)T∈R3，σ :R →R 是一个严格递增连续可微函数，且满足以下性质：

性质1当时，σ(0)=0 且θσ(θ)>0；

性质2对于θ ∈R，，其中σb>0；

性质3对于θ ∈R，函数有界.

如果ε 全局有界且ε →0，那么θ ˙θ 也全局有界，且

引理4[13]Yong’s 不等式

对于任意ε>0、任意两个维度相同的向量x 和y 来说，它们之间满足下列不等式：

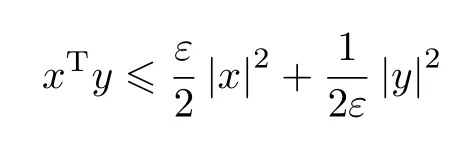
引理5[14]Jensen’s 积分不等式

对于任意正对称常数矩阵M ∈Rn×n，标量a 和b 满足a < b，向量函数f : [a,b]→Rn，使得皆有意义，则有

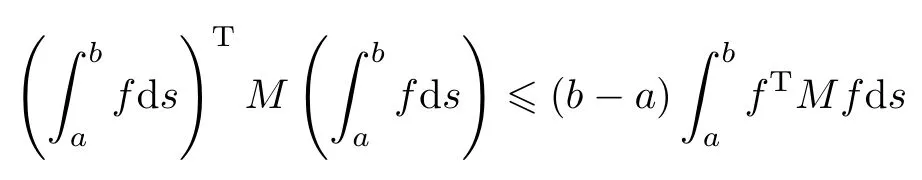
引理6提取算法[15]

若中间控制输入Fi:=(µ1,µ2,µ3)T, 对于任意xg，皆满足Fi(0,0,x)T，那么可由中间控制输入量Fi推导出无人机的推力Λi和目标姿态Qdi

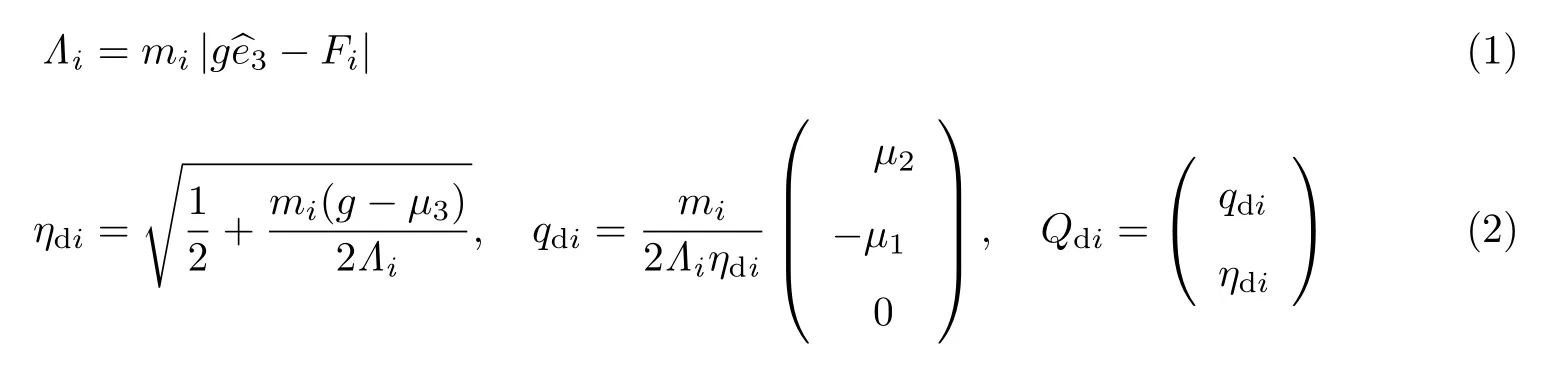
另外，在中间控制输入Fi可微的前提下，可将无人机的目标角速度ωdi定义为ωdi=Ξ(Fi) ˙Fi.

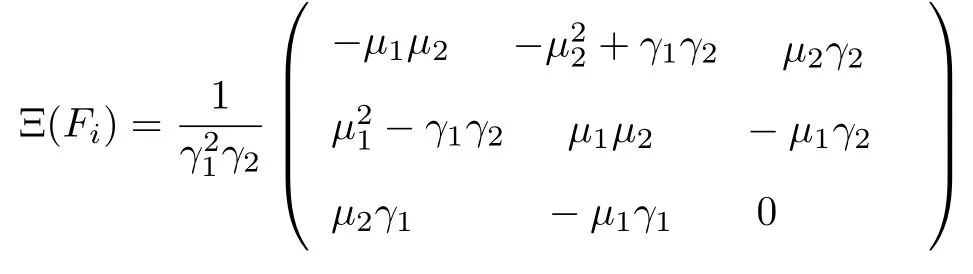
式中，γ1=(Λi/m)，γ2=γ1+(g −µ3).

2 系统模型

2.1 无人机动力学模型

建立一个由n 架垂直起降无人机组成的多无人机编队系统的数学模型[16]

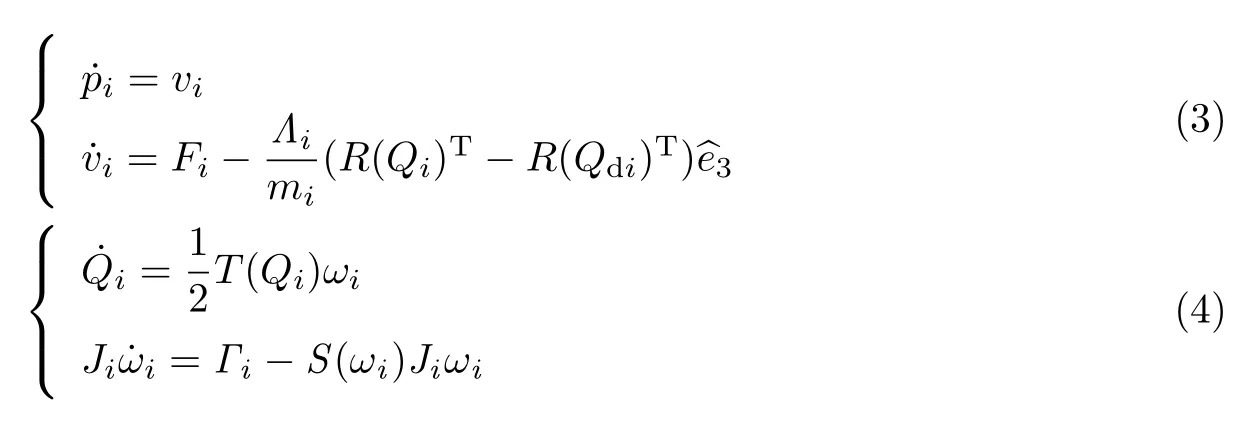
式(3)为多无人机组的平移动力学模型，式(4)为旋转动力学模型.其中，i ∈N :={1,··· ,n}，n 为编队中无人机数目；pi∈R3，vi∈R3分别表示第i 架无人机的重心位置和线速度；单位四元数Qi为第i 架无人机的姿态；ωi∈R3为第i 架无人机的角速度；mi为第i 架无人机的质量；J ∈R3×3表示机体相对坐标系的对称正定常数惯性矩阵；Λi∈R3，Γi∈R3分别表示作用于第i 架无人机的推力与输入力矩；表示地面坐标系下的单位向量且=(0,0,1)T；Fi∈R3表示待设计的第i 架无人机的中间控制输入.

在式(3)和(4)中

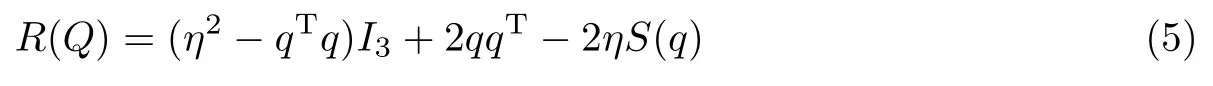
表示与单位四元数Q 相关的旋转矩阵，其中

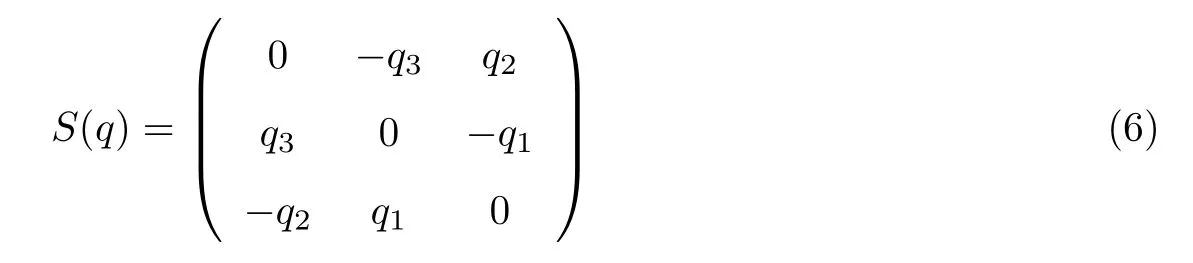
表示与单位四元素Q 的向量部分q 相关的斜对称矩阵，T(Q)为

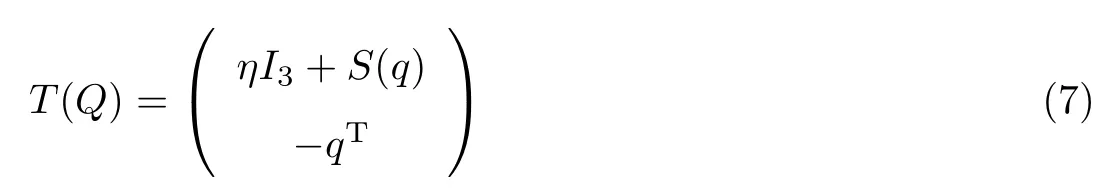
2.2 姿态误差动力学模型

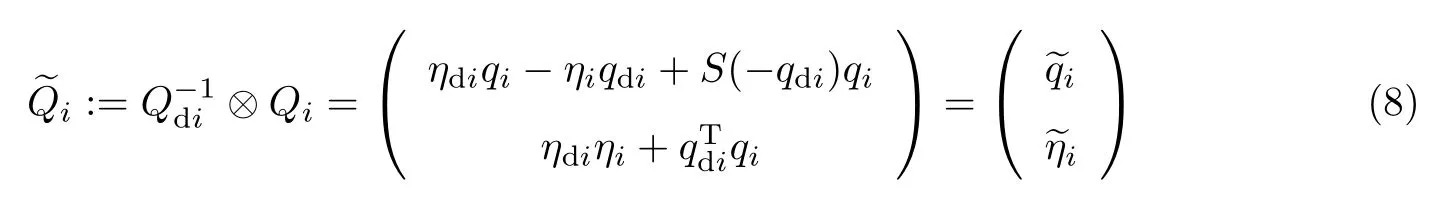
姿态跟踪的目标使Qi→Qdi或根据四元数的特性可知Qi与−Qi代表相同姿态，只是其中一个绕特定轴旋转2π，故对应相同的姿态.

由式(8)可推算出

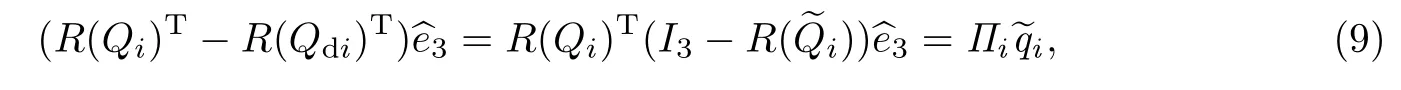
式中

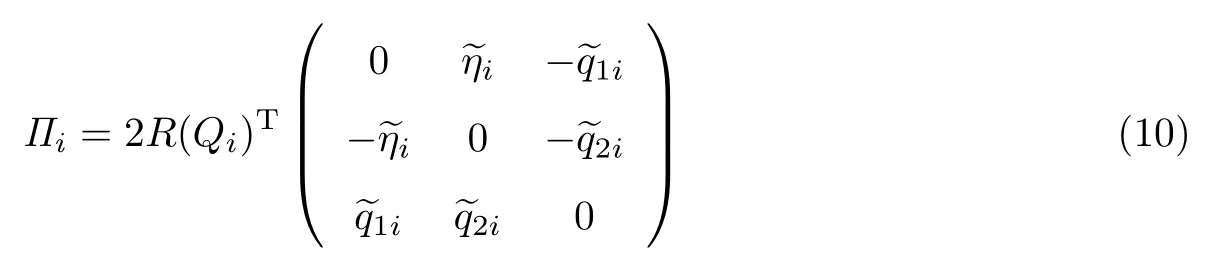
3 时延相关的编队控制方案

本文的目标是设计一种控制方案，使得无人机之间的信息传输可能存在时延的前提下达到预设的编队目标且保持悬停状态，即

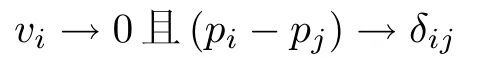
其中，δ1= (2,2,0)T表示第i 架无人机与第j 架无人机在编队中的相对距离，它定义了编队模式.无人机的控制结构如图1 所示，首先根据无人机间的相对距离δij以及接收到的邻居信息pj为第i 架无人机设计中间控制输入Fi；然后根据引理6 提取出推力Λi和目标姿态Qdi，提取的推力可以作为无人机平移动力学模型式(3)中的输入，使得无人机线速度vi→0，第i 架无人机和第j 架无人机相对位置(pi−pj) →δij；最后将目标姿态Qdi看作旋转动力学模型式(4)的参考输入，可以通过设计无人机的输入力矩Γi使得无人机的姿态Qi收敛于目标姿态，即第i 架无人机的角速度误差→0，姿态误差→0.

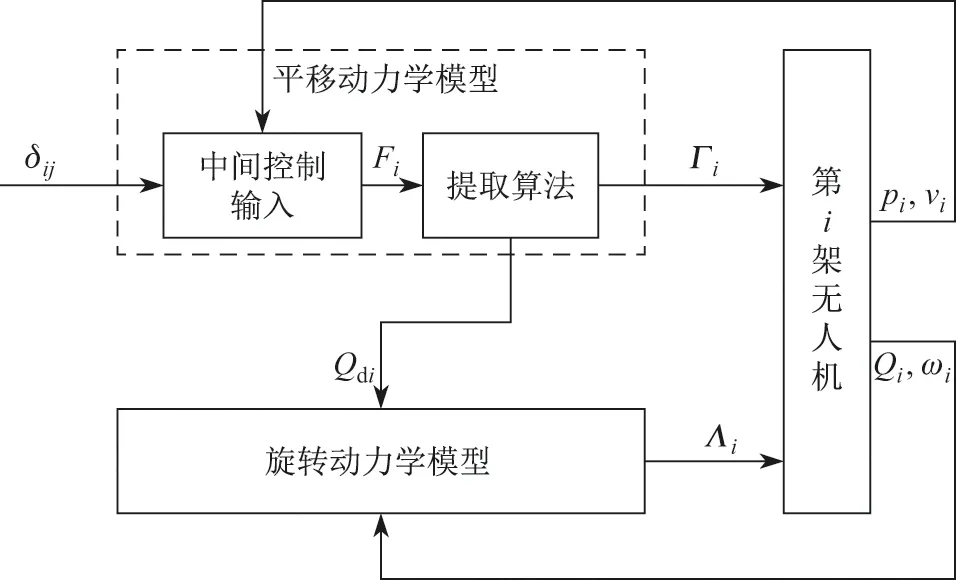
图1 无人机控制结构Figure 1 UAV formation control structure

3.1 中间控制输入设计

设计式(3)中的中间控制输入Fi，其中g 表示重力加速度.定义位置误差和速度误差分别为

式中，θi∈R3和αi∈R3为设计变量，变量θi、αi及其一阶微分可任意初始化.

设计第i 架无人机的中间控制输入Fi为

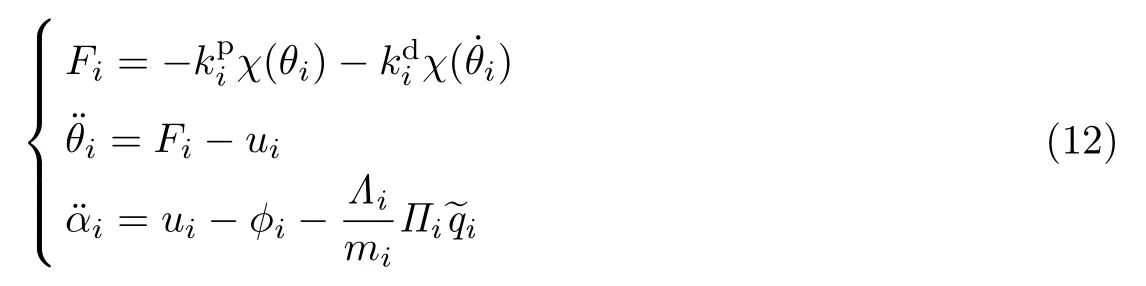
考虑到无人机之间信息传输时延发生的随机性，将φi设计为

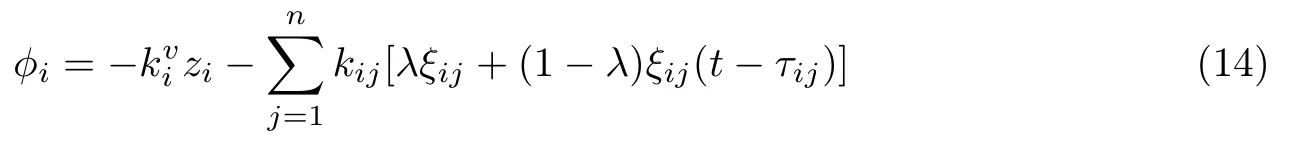
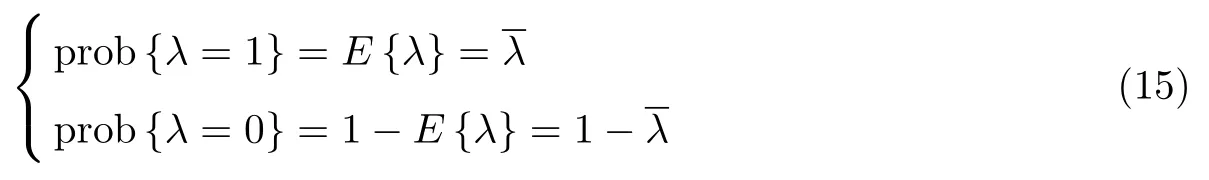
随机变量λ ∈[0,1]服从Bernoulli 分布[11]λ = 1 表示没有通信时延，其误差变量可定义为ξij(t) = ξi−ξj−δij；λ = 0 表示出现通信时延，其误差变量可定义为ξij(t −τij)=ξi−ξj(t −τij)−δij.

一旦得到中间控制输入Fi，便可根据引理6 推导出平移动力学模型式(3)中必要的推力Λi和目标姿态Qdi，从而求出式(3)中的重心位置pi和线速度vi.

与文献[16]相比，本文将一定发生的通信时延考虑为可能发生的通信时延，以服从Bernoulli 分布的随机变量描述是否发生通信时延，这符合实际的通信状况[17-18].本文研究了具有时变通信时延的多无人机编队控制和不具有通信时延的多无人机编队控制两种情况，兼顾了无人机编队系统的理论与实际，使得系统更具有实践意义.

3.2 输入力矩设计

考虑旋转动力学方程式(4)，为实现对目标姿态Qdi的跟踪，设计飞行器的输入力矩Γi为

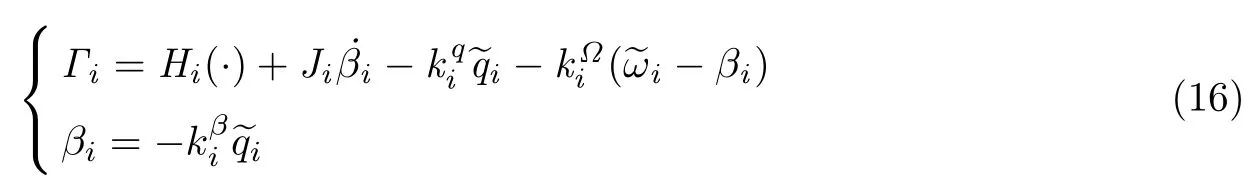
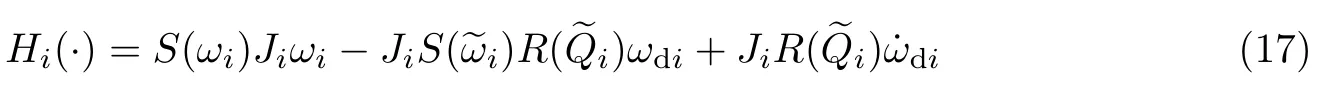
4 稳定性证明

第3 节给出了每架无人机的推力和输入力矩的设计方法.为了得到多无人机的编队飞行，本节将给出式(12)∼(14)与式(16)中各参数的设计方法，并分析多无人机系统编队控制的稳定性.

定理1由式(3)和(4)建立无人机动力学模型.由引理6 提取算法得出推力输入Λi和目标姿态Qdi，由式(12)∼(14)给出中间控制输入Fi，由式(16)给出转矩输入Γi.假设无人机之间的连接图是无向且连通的，则对于某一个ε > 0，待设计的正标量增益以及分别满足式(18)和(19)

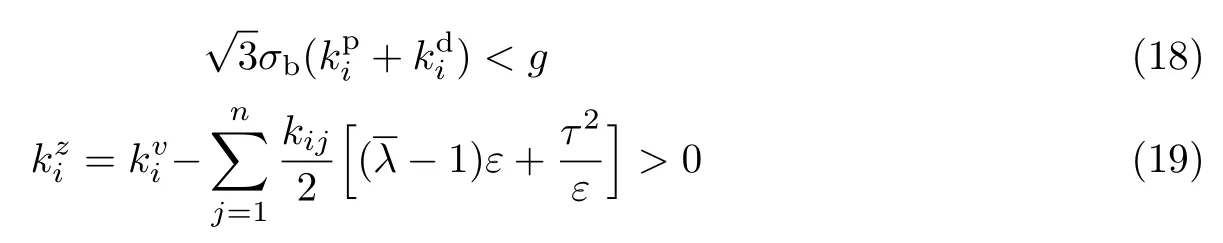
证明由式(12)可得

σb为σ(·)函数的上界，即式(20)说明中间控制输入Fi是先验有界的.Fi还需满足提取算法的条件，即对于任意的xg，有满足定理1 中第1 个不等式.

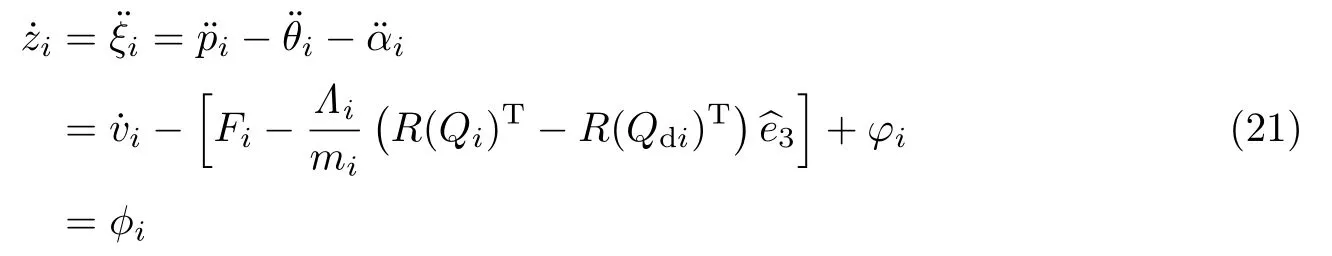
由式(14)可得

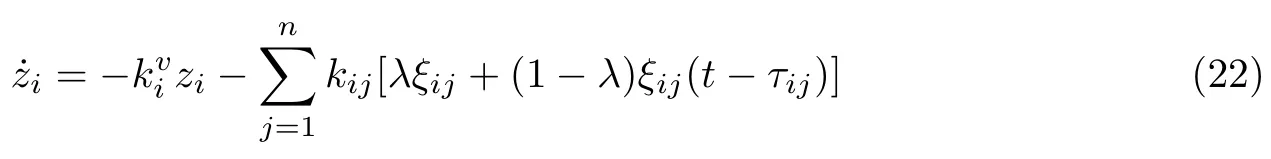
定义姿态跟踪误差Ωi为

则姿态跟踪动力学为

由式(22)和(24)可以看出，姿态误差动力学与平移误差动力学之间是相互解耦的，因此可以单独完成两个动力学子系统的稳定性分析.

首先考虑姿态误差动力学的稳定性.选取类李雅普诺夫函数为

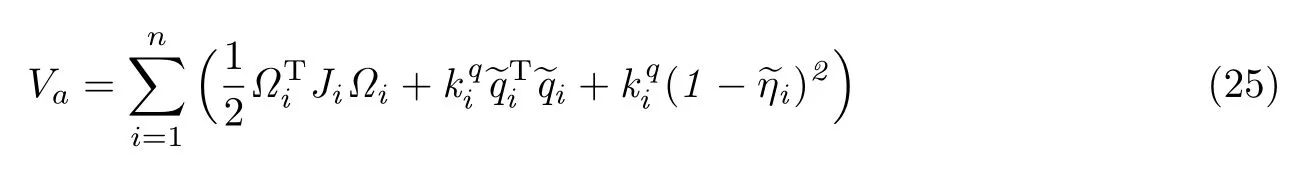
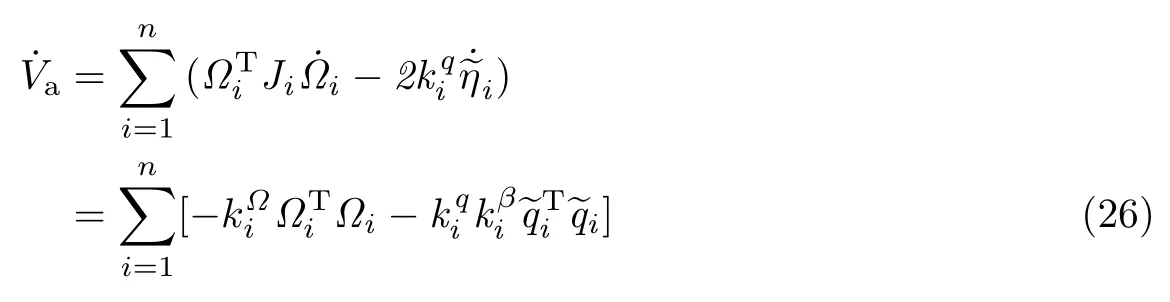
然后根据平移误差动力学方程，建立类Lyapunov-Krasovskii 泛函为

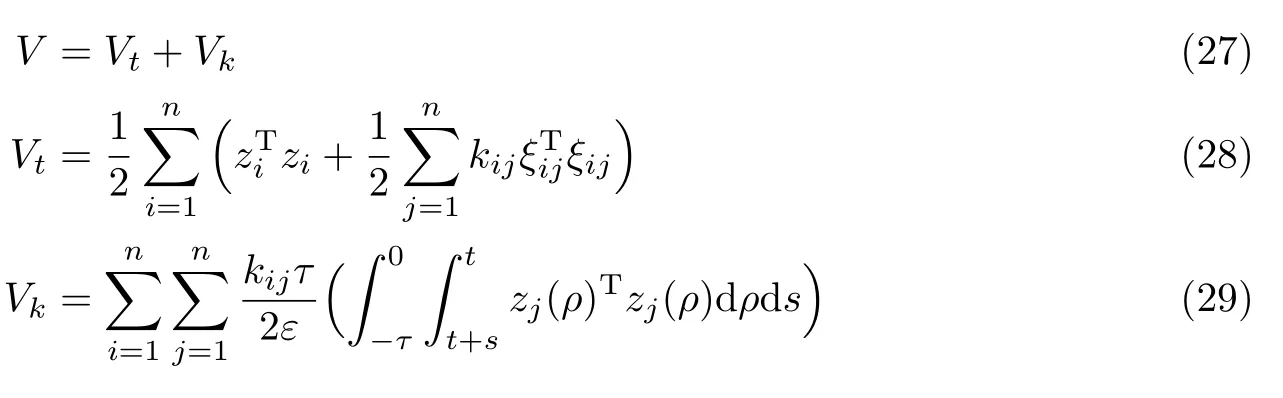
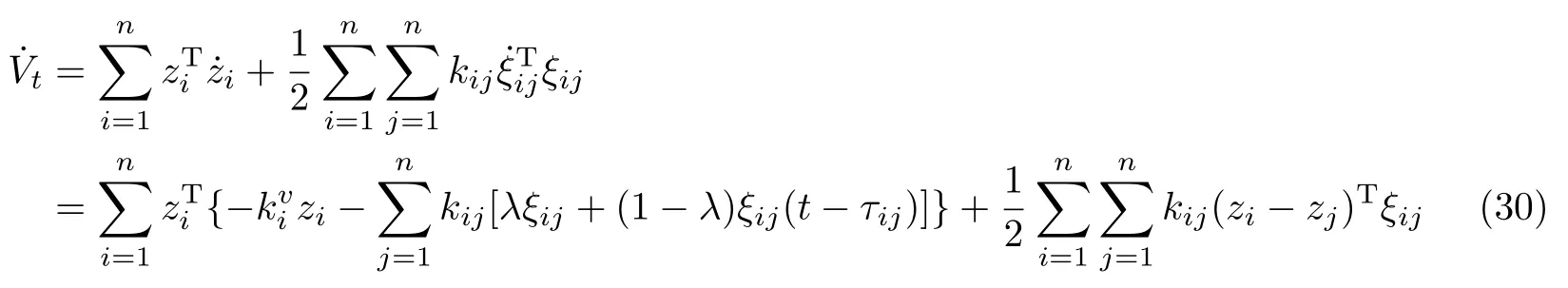
因为ξij=−ξji且kij=kji，所以可得

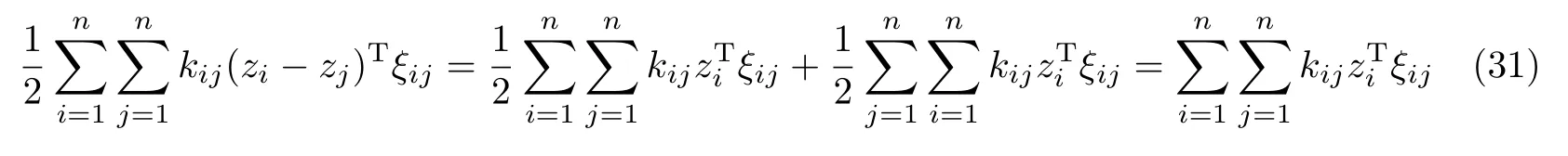
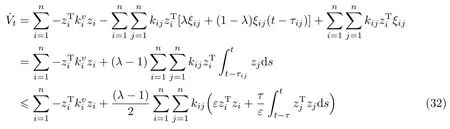
接着对式(29)求导可得

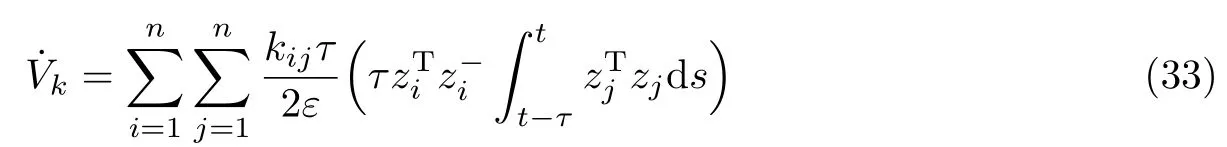
对式(27)求导可得

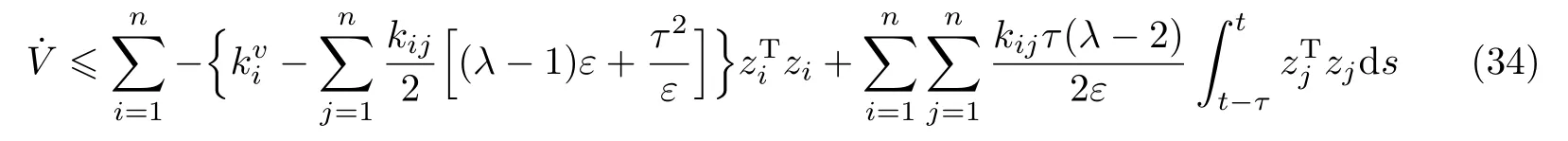
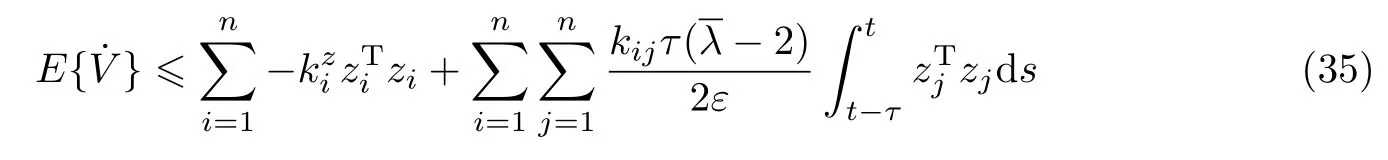
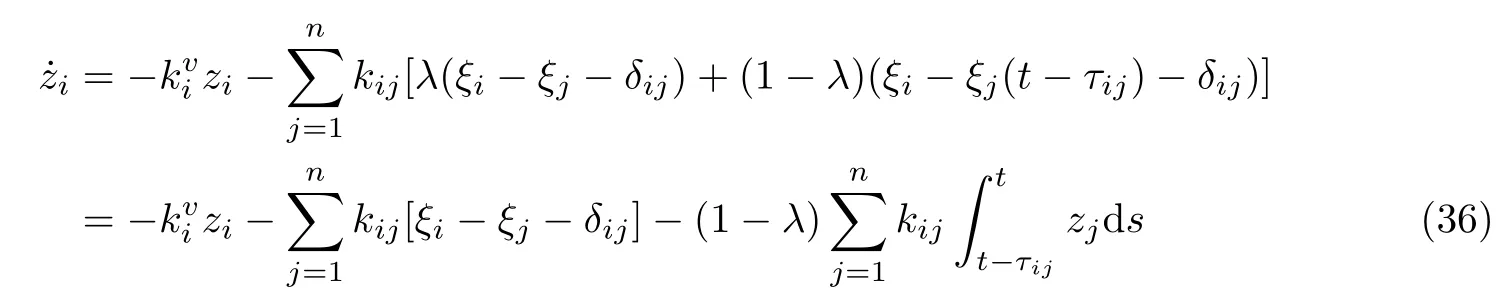
式(37)等价于

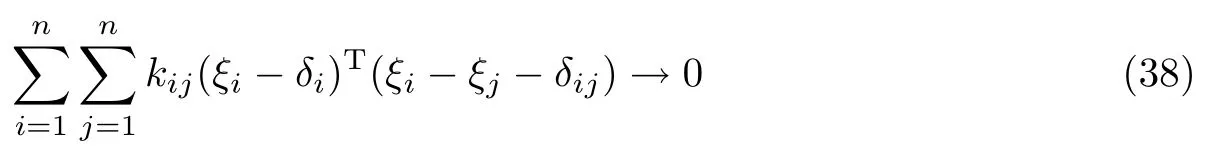
式中，δi表示第i 架无人机相对编队中心的目标位置，由δij=δi−δj可知

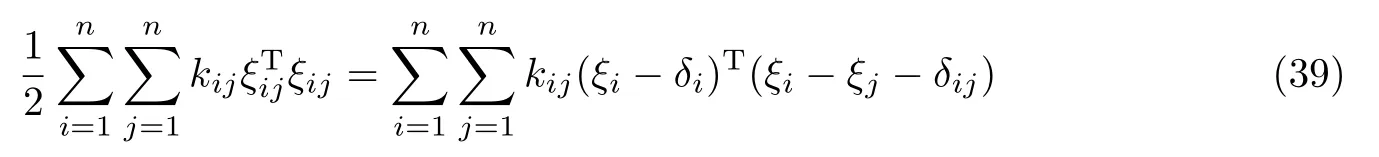
得到ξij→0，即(ξi−ξj)→δij.

式(12)可化为

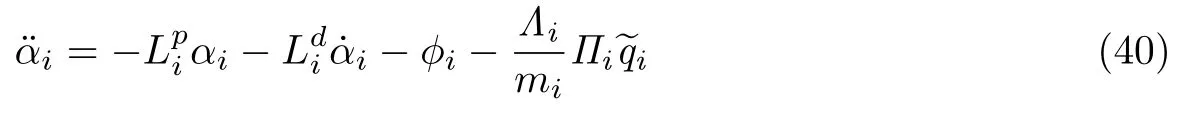
式(40)代表一个稳定二重积分器的动力学，它有一个全局有界且渐近趋于0 的摄动项φi+因此，αi和皆有界，并且αi→0，

式(12)中θi的动力学模型可以简化为

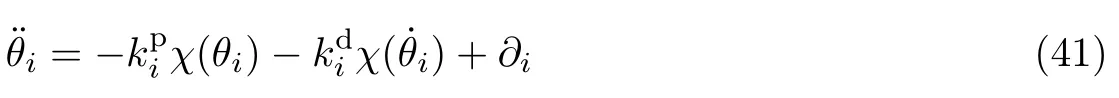
5 仿真实例

在本次仿真中，n = 4，即编队中的无人机数目为4，组成一个与地面平行的正方形编队.编队的形状由δij来定义，δij=(δi−δj)，(i,j)∈γ，δi的值定义如下：

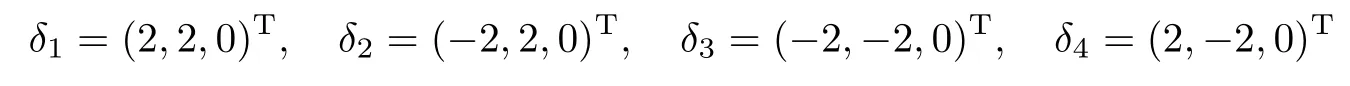
无人机之间的通信流图是固定、无向且连通的.考虑邻接矩阵K，当(i,j) ∈γ 时，kij=0.5，否则kij=0；边集γ ={(1,2),(1,3),(2,3),(2,4)}.

无人机动力学模型为式(1)和(2)，其中mi= 3 kg，Ji=diag(0.13,0.13,0.04)kg·m2，i ∈N :={1,··· ,4}.各个元素的初始值如下：

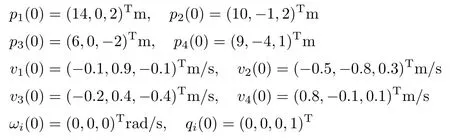
变量θi、αi及其一阶微分初始值分别为

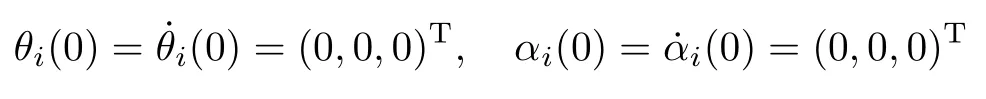
时变通信时延定义为τij(t) = 0.2|sin(0.5t)|s，(i,j) ∈γ，当其上界τ = 0.2 s 时满足定理1 中的式(16)和(17).在函数χ中，σ(·) = tanh(·)，σb= 1.系统中各个正标量增益赋值如表1 所示.

表1 控制增益量Table 1 Control gains

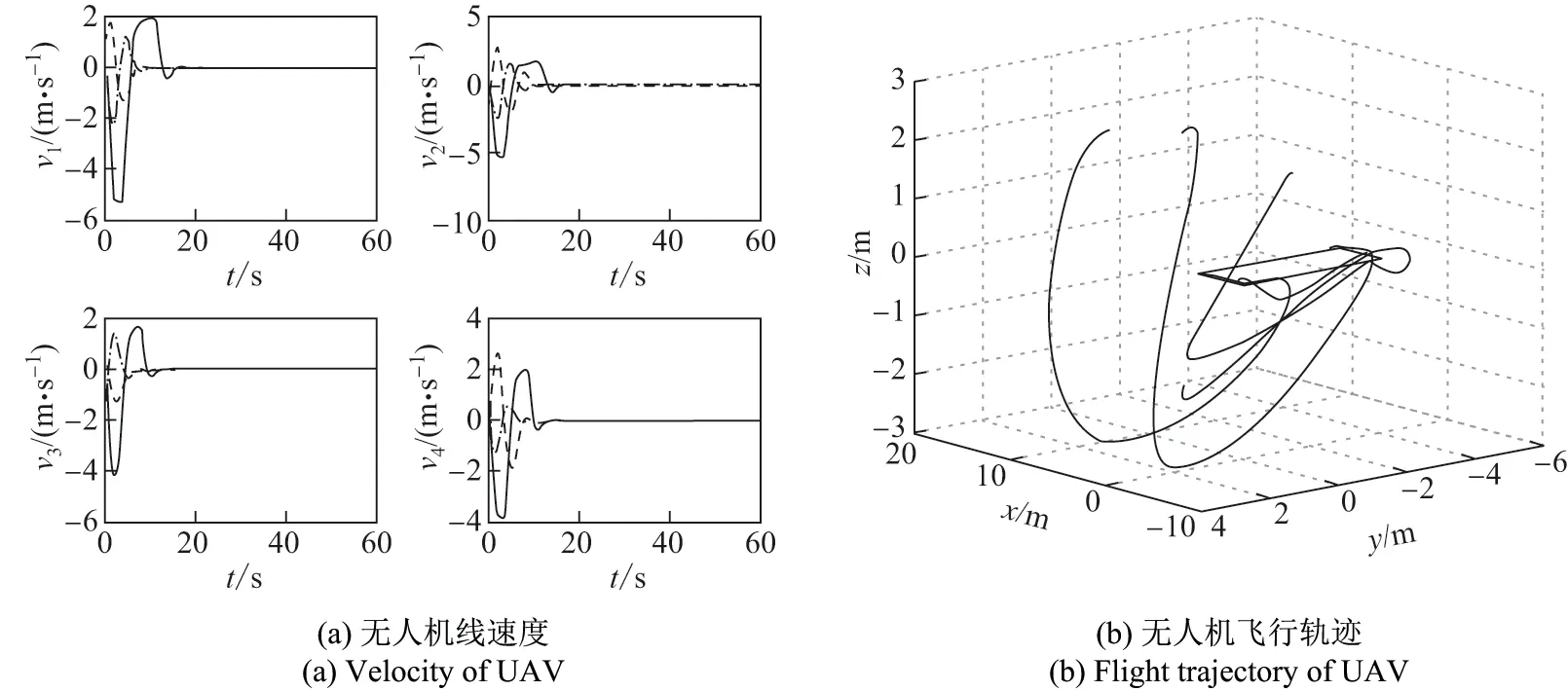
图2 时的无人机编队仿真结果Figure 2 Simulation results of UAV formation when

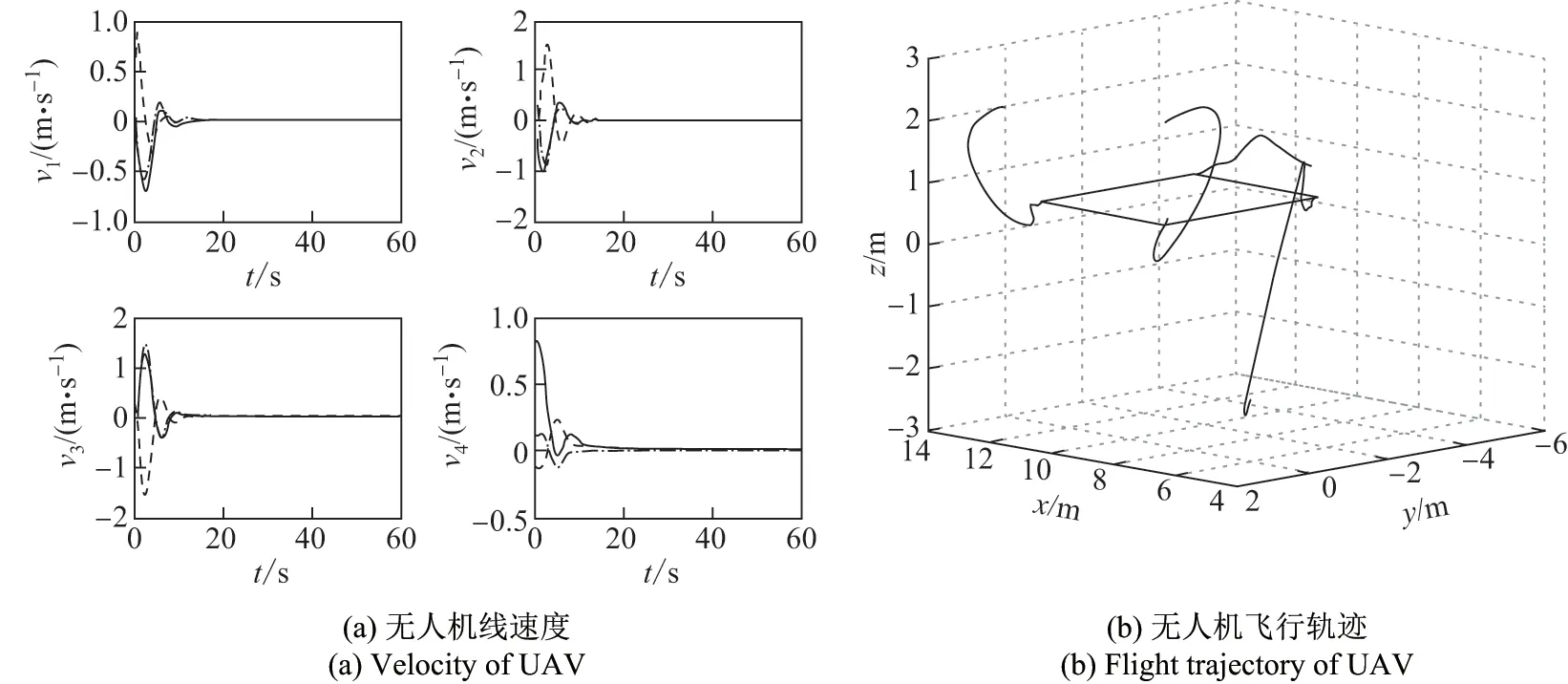
图3 时的无人机编队仿真结果Figure 3 Simulation results of UAV formation when

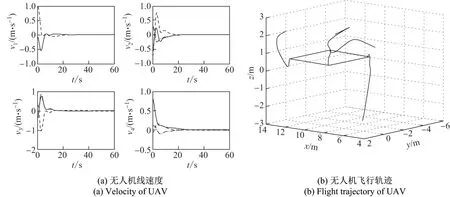
图4 时的无人机编队仿真结果Figure 4 Simulation results of UAV formation when

6 结 语

本文考虑了无人机之间信息传输时延是随机发生的情况，研究了多无人机编队控制问题.利用Bernoulli 随机变量描述是否发生信息传输时延，使用四元数描述无人机的姿态动力学，根据提取算法获得无人机在预设队形下的目标姿态.设计了无人机平移运动中的推力，以及旋转运动中的转矩输入，使得多个无人机在信息传输存在随机时延时依然能够实现预定的队形.最后，利用数值仿真验证了本文所设计的编队控制器.

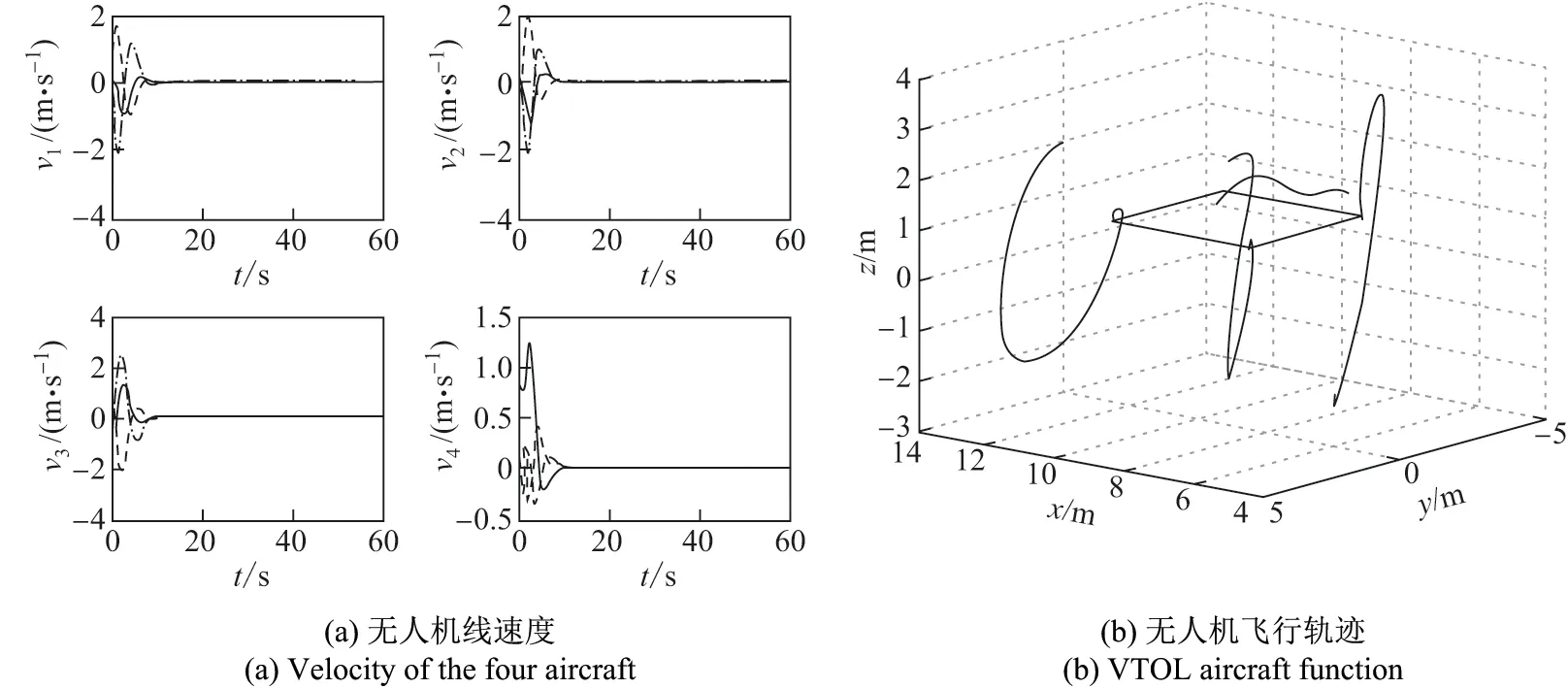
图5 无人机编队仿真结果Figure 5 Simulation results of UAV formation when