碳纤维复合材料平板分层缺陷的MIT检测
曹 峰,周庆祥,邱国云,李广凯
(中车青岛四方机车车辆股份有限公司,山东青岛 266111)
0 引言
碳纤维复合材料(Carbon fiber reinforced plastics,CFRP)[1-2]大量作为中央翼盒、机身等重要受力构件,且长期受到高强度、高负荷和大摩擦的冲击而存在安全隐患。此外,预浸料中的低分子杂质、溶剂和水分容易挥发而导致碳纤维复合材料表面和内部形成空隙、裂纹、分层等缺陷[3]。因此,CFRP平板构件的结构质量检测对于维护航空领域关键部件的安全运行具有重要的意义。
目前,超声波检测[4]、X射线检测[5]、工业CT检测[6]等技术已用于碳纤维复合材料结构件的缺陷检测,但由于超声波检测需要耦合剂,X射线检测具有辐射性,工业CT设备笨重且精度低而存在局限性。基于涡流检测原理的磁感应断层成像[7](magnetic induction tomography,MIT )新技术通过重建图像获得被测对象电导率或磁导率分布特征而辨识出缺陷,具有无耦合、无接触、无侵入且能直观显示被测对象损伤等特点而备受关注。
文献[8]设计了6种线圈方向:半径r向、圆周φ向、z轴向、r与z向、r与φ向以及φ与z向对MIT探头进行研究,发现两个方向组合方式检测效果要优于单个方向。基于此项研究,文献[9]采用其中一种两线圈垂直放置方式的结构组成MIT多通道探头对CFRP结构件进行检测,并应用Tikhonov正则化算法实现了18 mm×18 mm×1.4 mm体积缺陷图像的重建。北京交通大学刘泽团队[10-12]对于MIT法检测CFRP材料开展了大量的研究:文献[10]采用环形阵列线圈对复合材料平板构件进行检测,但环形阵列中心位置磁场强度较弱容易造成缺陷的漏检;文献[11]针对被检对象的不同形状设计了全包围式“O”型、半包围式“C”型及倒“L”型MIT探头,为MIT传感器的结构设计提供了参考;文献[12]以改进Tikhonov正则化重建算法的方式提高了重建图像的精度和质量,同时为正则化因子的选择进行了分析。上述研究为本文MIT探头的设计提供了参考,但对于CFRP中分层缺陷的MIT检测报道较少。厦门大学刘小华[13]基于仿真研究以旋转涡流探头方式检测出CFRP中纤维弯曲缺陷,并实验验证了方向性探头辨识出纤维角度的有效性,但对于分层缺陷引起的z轴方向的纤维弯曲并不适用。南京航空航天大学邹雨峰[14]应用多频涡流C扫检测出复材板2 mm的隐藏裂纹,但裂纹为铣刀加工与实际分层缺陷存在差异。
基于上述分析,本文采用激励线圈与检测线圈方向垂直的MIT探头对碳纤维复合材料平板构件内的分层缺陷进行检测。通过对MIT原理的分析,建立三维有限元模型,测试探头检测性能以确定最佳频率,从而计算出高准确度的灵敏度矩阵;设计组建CFRP平板构件MIT检测系统,开展缺陷检测试验得到缺陷数据,从而应用图像重建算法实现缺陷的直观评判。
1 磁感应断层成像原理
磁感应断层成像可分为正问题和逆问题[15]。正问题为已知被测材料的磁导率和电导率分布,根据麦克斯韦方程组求解检测线圈的感应电压,如式(1):
S·σ0=V0
(1)
式中:S为灵敏度矩阵,由被测对象不同区域的检测线圈感应电压测量值构成;σ0为已知被测材料的电导率;V0为检测线圈对CFRP分层缺陷的感应电压测量值。
MIT中逆问题与正问题相反,即根据检测线圈的感应电压测量值通过重建算法对被测材料电导率的分布进行图像重建,如式(2):
σ=S-1·V
(2)
式中:σ为重建电导率;V为缺陷处检测线圈感应电压测量值。
在逆问题的求解过程中,由于S求逆存在病态性,本文首先根据式(3)简化处理数据,而后采用Tikhonov正则化算法式(4)进行图像重建以提高重建图像的质量。
S=(S-Ve)/Ve
(3)
σ=(ST+λI)-1STV
(4)
式中:Ve为材料板完好无损时所测得的灵敏度矩阵;I为与S同等大小的单位矩阵;λ为正则化因子。
由上述分析可知,正问题为逆问题的解决提供了数据资源库,因此,正问题中数据的测量和灵敏度矩阵计算的精准度对逆问题成像质量的影响极其重要,这就要求MIT探头具有较高的检测灵敏度。
由于MIT是基于涡流检测的一种新技术,如果在激励线圈通交流电激发主磁场B,根据电磁感应原理,在被检对象中感生出涡流从而产生次级磁场ΔB。其中,ΔB与B存在式(5)所示的正相关关系:
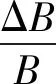
(5)
式中:ω为激励源的角频率;ε0为真空介电常数;εr为相对介电常数;σ为被测对象的电导率。
而ΔB虚部由涡流感应产生,该参数与材料的电导率分布及施加在激励线圈上的频率的大小成线性关系[16]。因此,本文采集检测线圈感应电压的虚部分量数据进行分析以反映设计的探头对碳纤维复合材料平板的缺损的感应。
2 仿真模型与灵敏度矩阵
2.1 仿真模型与计算分析
在MIT中,主磁场B远大于次级磁场ΔB,本文采用激励-接收型探头,且激励线圈与检测线圈方向相垂直的设计以补偿的方式减弱了MIT探头对主磁场的敏感度[9],提高探头对试件损伤的敏感性。同时,这与文献[8]对线圈放置方式的研究结果相符合。
以单向碳纤维复合材料平板为研究对象建立MIT检测的三维有限元模型如图1所示,其中CFRP平板尺寸为:150 mm×90 mm×2 mm(长×宽×厚),电导率为58.8×10-6S/m;圆柱形激励线圈与跑道型检测线圈的参数为:内径为2 mm,外径为4 mm,匝数为50,线径为0.06 mm,高度为2 mm,跑道型线圈总长度为8 mm,间距为3 mm;数值分析计算参数为:提离为0.5 mm,相对磁导率为1,激励电流为1 A。
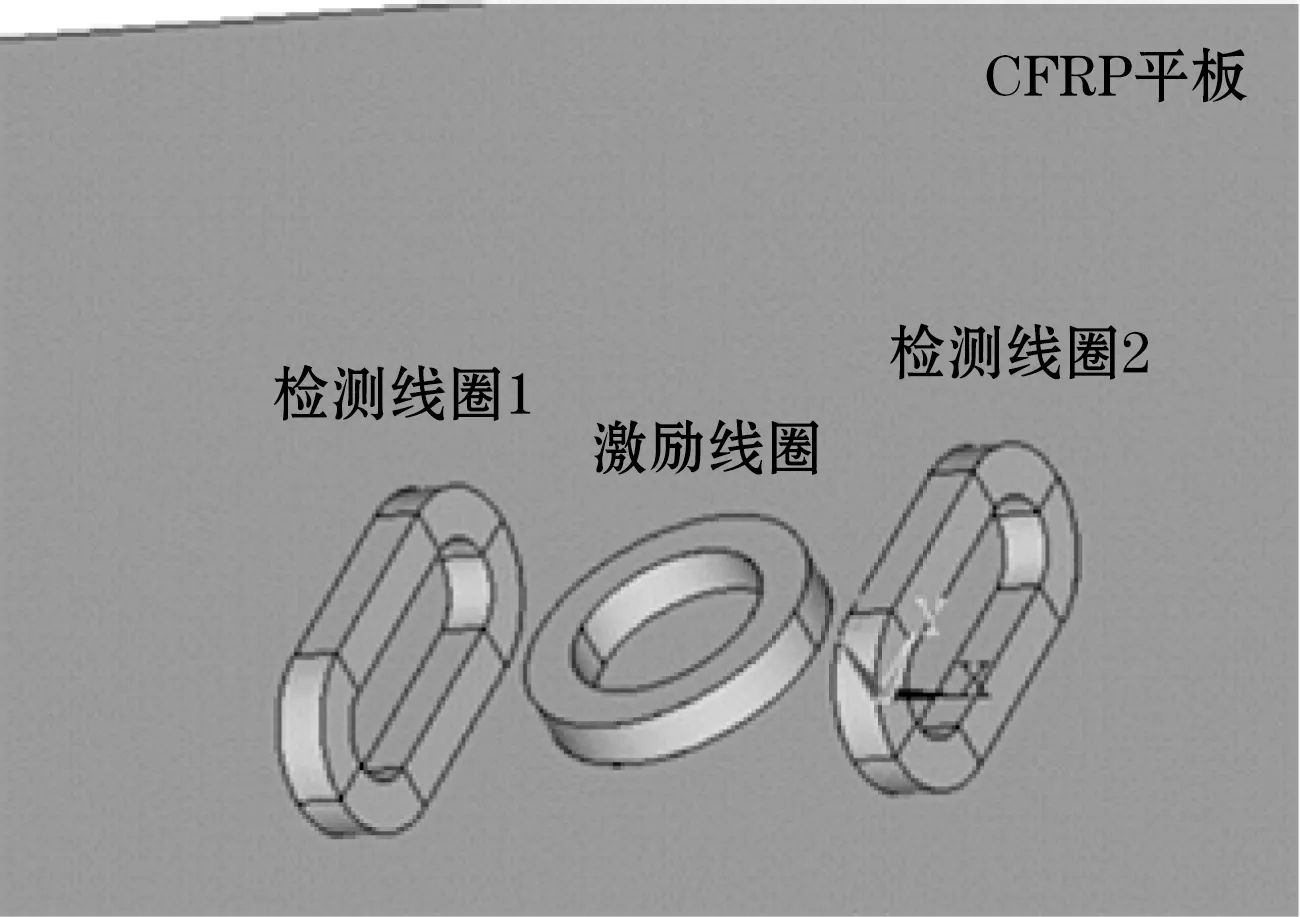
图1 MIT涡流探头模型
由于绝大部分磁场集中在线圈直径3倍尺寸模型范围内,故设置近场空气域为线圈直径的40倍[17]及同等大小的远场空气域以消除磁场的阶段效应,模拟磁场在空气中的衰减。定义材料属性时设置缺陷为10 mm×10 mm×0.5 mm,电导率为0。继网格划分之后,在模型区域边界施加狄里克莱边界条件使得磁通量平行于边界,进行耦合与求解计算,经由后处理模式得到数值分析结果。
选择不同频率对MIT探头检测性能进行测试研究,同时,为计算准确度较高的灵敏度矩阵奠定基础。设定探头检测线圈1在无缺陷处测量值为V0;在缺陷处测量值V1;ΔV为两者之差;得到200、500、800、1 000、1 200、1 500 kHz测量结果,如图2所示。

图2 不同频率测量结果
由图2可知,ΔV随着频率的单调增加呈现先增加后减小的趋势。其中,200~500 kHz阶段急剧增加;而500~1 000 kHz范围内增加缓慢,1 000 kHz时达到最大值4.7 mV;在1 000~1 500 kHz阶段又缓慢减小。这说明MIT探头在200~500 kHz范围内对测量值大小影响巨大,故此范围内频率不合适;而在500~1 500 Hz范围内对测量结果影响较为轻微,为适宜选择频率;由于MIT探头对于CFRP在1 000 kHz时检测效果最佳,故本研究选择频率为1 000 kHz。
2.2 灵敏度矩阵的计算
基于探头最佳检测频率开展灵敏度矩阵的仿真计算。根据Geselowitz理论灵敏度矩阵S可由式(6)表示[10]:
S=(ΔV/I)Δk
(6)
式中:ΔV为测量电压值;I为激励线圈电流;Δk为敏感场内任一个小区域内的复电导率变化。
为了简化灵敏度矩阵获取过程,取平板中心位置60 mm×60 mm×2 mm区域为敏感区域,定义5 mm×6 mm×2 mm为单元灵敏度域,则共120个单元灵敏度域。由于MIT探头包含2个检测线圈,因此灵敏度矩阵S为120×2的矩阵。根据式(3)对灵敏度矩阵数据处理后得到检测线圈1、2对敏感区域的测量结果如图3所示。

(b)检测线圈1线圈位置与灵敏度场

(c)检测线圈2测量灵敏度场
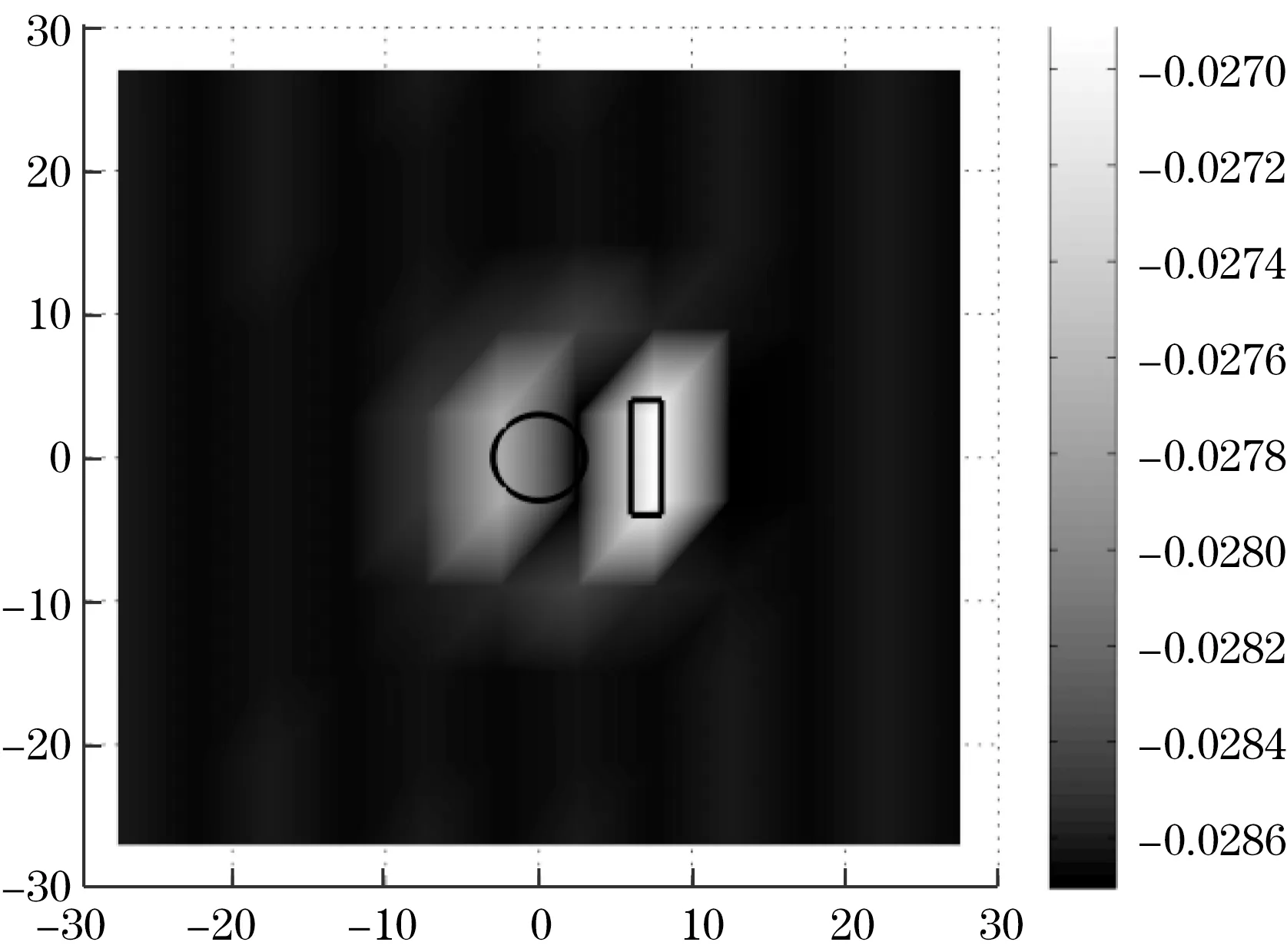
(d)检测线圈2线圈位置与灵敏度场图3 检测线圈对灵敏度场测量结果
图3显示灵敏度场仅在激励、检测线圈下方出现剧烈的凸起;且检测线圈下方敏感域凸起明显高于激励线圈下方,这表明MIT探头能够有效辨识缺陷区域与非缺陷区域,且信号清晰,易于辨识,即说明此MIT探头测得的灵敏度矩阵具有较高的准确度。
3 试验与图像重建
3.1 CFRP平板分层缺陷检测试验
试块由碳纤维预浸料铺层后经热压机加热加压固化而成,采用8层碳纤维布同向铺层,且在缺陷位置处放置聚丙烯片以模拟分层缺陷,如图4所示。试块#1-3尺寸为100 mm×90 mm×2 mm;对应缺陷#1-3的尺寸依次为10 mm×10 mm×0.5 mm、10 mm×10 mm×0.5 m、10 mm×10 mm×0.3 mm,且位于试块水平面中央位置如图4(a)所示;深度位置依次为0.5~1 mm,1~1.5 mm,0.5~1 mm,如图4(b)所示。
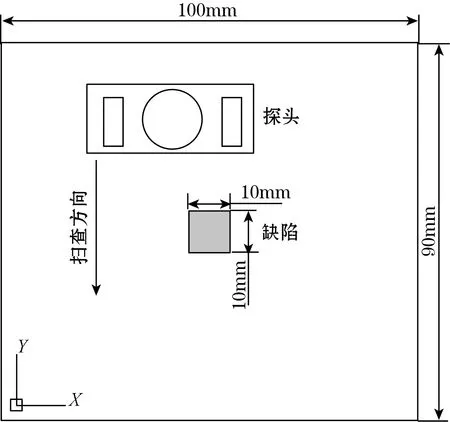
(a)试块#1-3缺陷水平位置示意图

(b)试块#1-3及缺陷图4 分层缺陷#1-3试块
MIT检测系统由锁相放大器、MIT探头、三维自动扫查装置和计算机构成,如图5所示。通过计算机编辑锁相放大器产生±5 V、1 000 kHz的正弦波作为激励信号接入MIT探头,设置扫查速度为4 mm/s完成CFRP平板材料y方向的自动扫查,而检测线圈拾取产生的感应信号经由锁相发生器进行滤波和数据采集(每秒299字符)后存入计算机进行处理与分析。

图5 MIT检测系统图
图6为缺陷位于检测线圈1正下方时MIT探头对CFRP平板分层缺陷检测结果,对于缺陷#1-3的感应电压测量值分别为V#1、V#2和V#3,相应最大值与最小值差分别为ΔV#1、ΔV#2和ΔV#3。

图6 检测线圈1检测缺陷#1-3结果
由图6可知,V#1、V#2和V#3变化趋势形同,在分层缺陷处都出现单波峰形状;但存在明显的高低峰值差别。这是由于分层缺陷的存在使得碳纤维布受到严重挤压而干扰了纤维丝的正常走向从而使得CFRP平板材料出现电导率不均匀的严重畸变,导致磁场发生改变,检测信号发生波动。又因为缺陷大小不同,使得纤维布受挤压程度不同,导致磁场变化不同而产生ΔV#1为0.796 mV;ΔV#2为0.453 mV;ΔV#3为0.286 mV。此外,已知缺陷#1与#2的长宽高都相同,仅埋深相差0.5 mm,而ΔV#1与ΔV#3相差0.51 mV;缺陷#1与#3的长度、宽度、埋深都相同,仅高度相差0.2 mm,而ΔV#1与ΔV#2相差0.343 mV。由此可知,埋深和缺陷高度不同导致缺陷信号减小的百分比分别为64.07%和43.09%,因此,缺陷高度和埋深是影响MIT检测信号虚部分量大小的重要因素。
3.2 CFRP平板分层缺陷图像重建结果与分析
基于灵敏度矩阵S与试验测得的缺陷信号测量值,根据Tikhonov正则化算法分析进行图像重建。取正则化因子λ为8,对分层缺陷#1-#3的重建图像如图7所示。
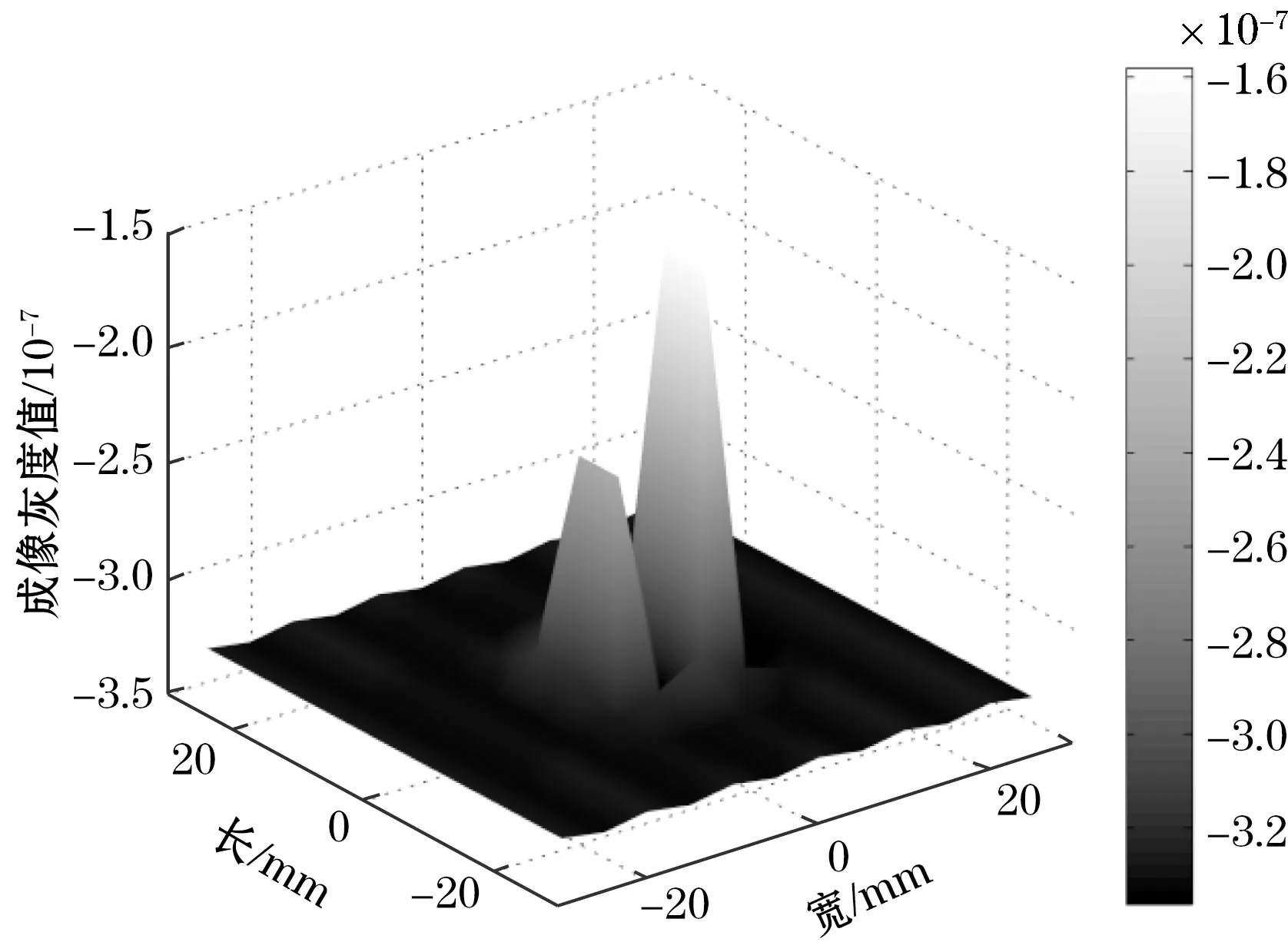
(a)缺陷#1重建图像
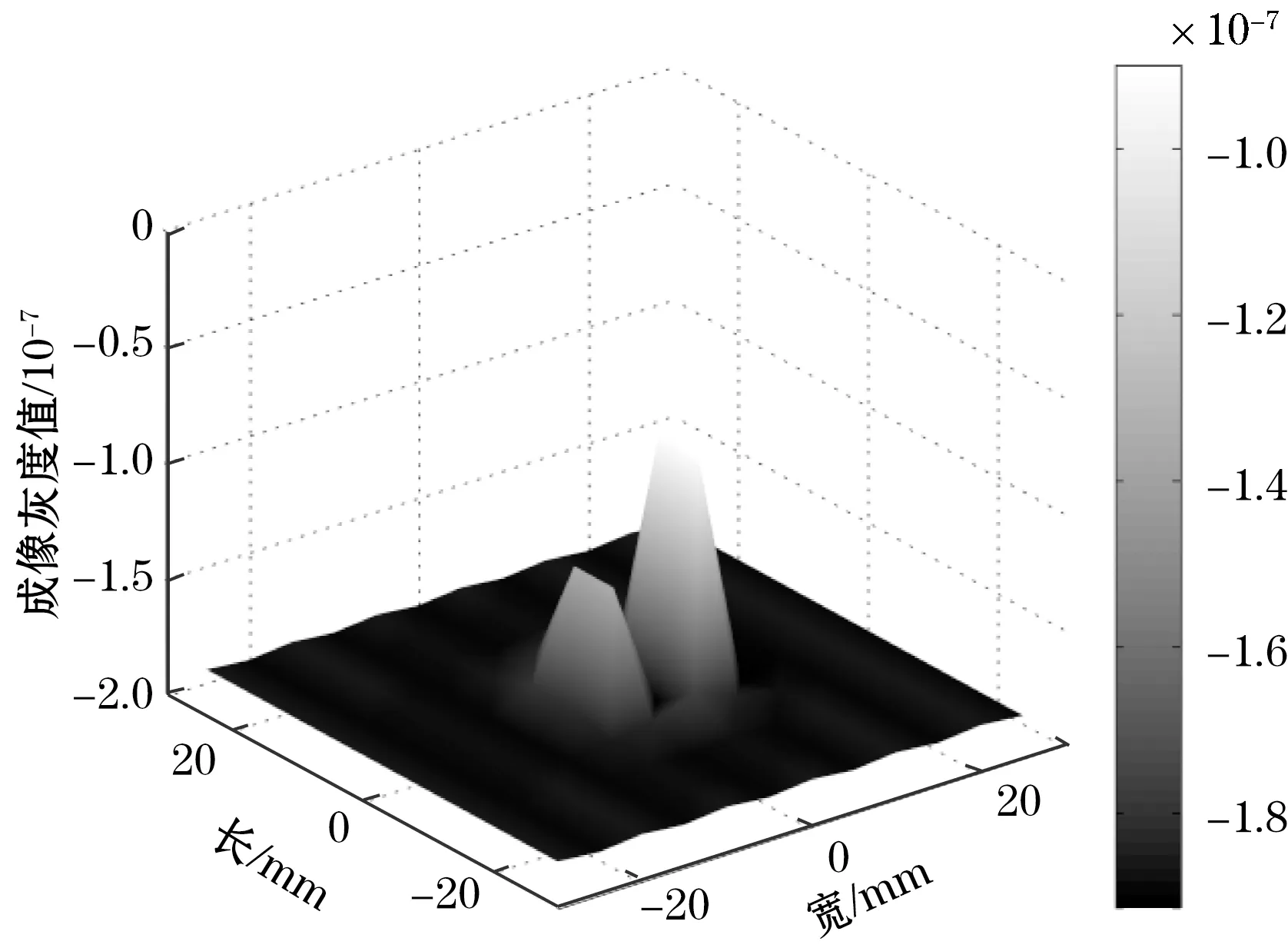
(b)缺陷#2重建图像
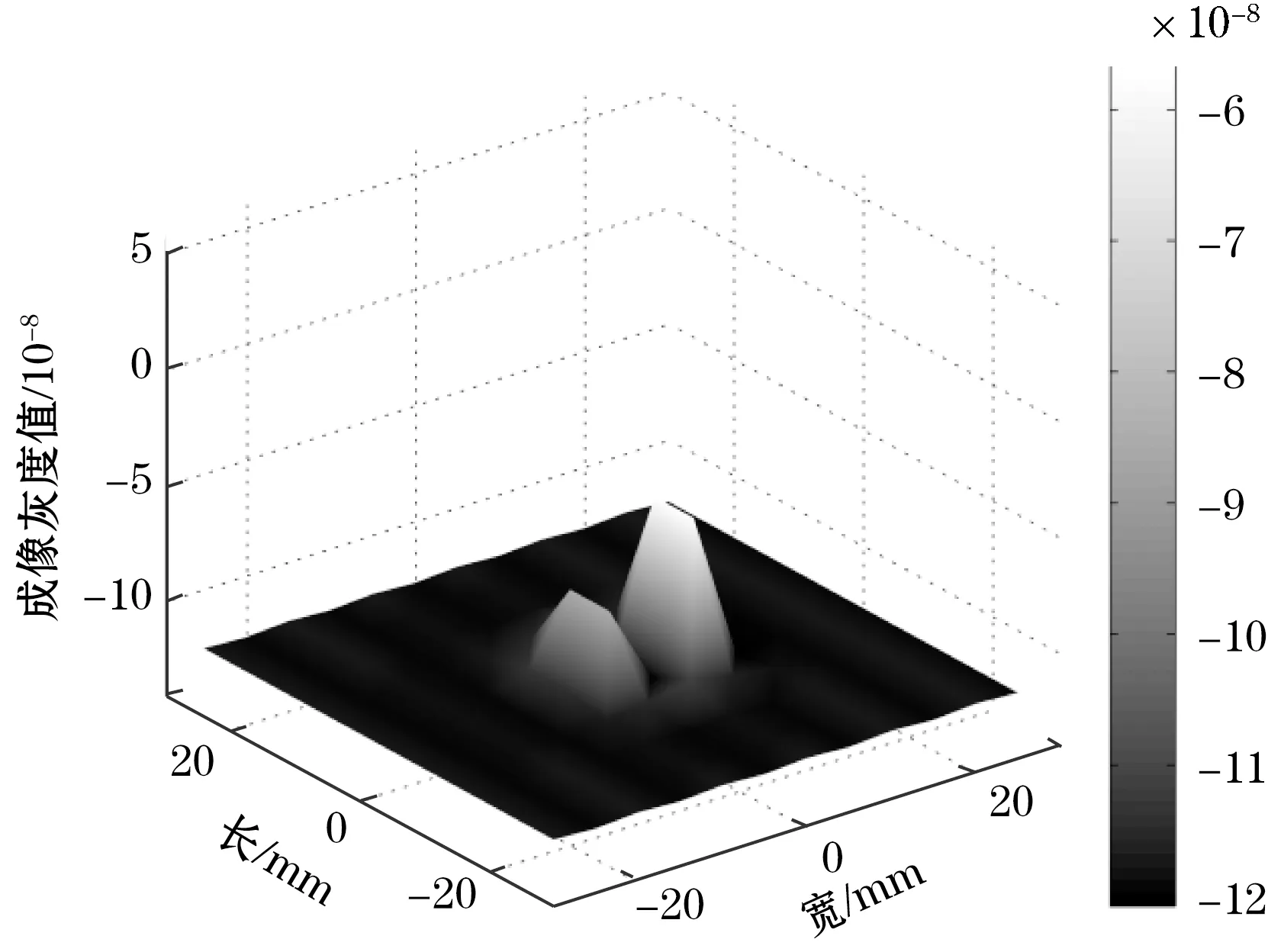
(c)缺陷#3重建图像、图7 Tikhonov正则化算法重建图像
图7显示,在复材板存在分层缺陷的位置处,重建图像中出现剧烈的凸起信号;且缺陷埋深越小,尺寸越大,重建图像中凸起现象越突出,缺陷信号特征越明显,如缺陷#1、#2、#3的成像灰度值分别为1.731 9×10-7、9.855 7×10-8、6.218 9×10-8。由此可知,重建图像能够识别出CFRP平板构件中分层缺陷所在位置,这表明Tikhonov正则化算法重建图像可以准确直观地辨别缺陷所在,同时说明了MIT方法检测CFRP平板构件中分层缺陷的有效性和直观性。
图像误差error是指重建图像与原始图像之间的相对误差,根据式(7)计算error对缺陷#1-#3重建图像质量进行评价。
(7)

得到缺陷#1-#3的图像误差分别为0.983 8、0.990 8、0.994 2,可见,随着缺陷信号特征量的减小,error逐渐增大,缺陷埋深或者尺寸越小,成像误差越大,识别难度越大。由此可见,以Tikhonov正则化算法对纤维增强复合材料平板构件中分层缺陷的图像重建不仅能够有效、可靠地识别缺陷,并且成像效果具有稳定的规律性。
4 结论
本文通过对MIT涡流探头结构的分析,设计了激励线圈与检测线圈垂直放置方式的MIT探头,并由三维有限元仿真测得探头最佳检测频率为1 000 kHz,从而计算出高准确度的灵敏度矩阵;应用Tikhonov正则化算法重建出缺陷图像,实现了MIT技术CFRP平板中埋深1 mm的10 mm×10 mm×0.5 mm与埋深0.5 mm的10 mm×10 mm×0.3 mm分层缺陷的有效识别和直观显示。因此,MIT技术对于CFRP平板构件中分层缺陷的检测具有重要的工程意义。

