锚头内部非对称横向作用力对植入式FBG传感器传感性能的影响分析
吴 俊,舒岳阶,傅志芳
(重庆交通大学,西南水运工程科学研究所,重庆 400016)
0 引言
缆索索力是反映缆索整体受力状态的关键指标,同时,锚头作为缆索最重要的承力结构,对其内部性能状态进行实时监测也尤为必要,为此,缆索索力与锚头内部性能状态的自感知成为“智能缆索技术”[1]的重要组成部分。
文献[2]通过对缆索全长沿程力学特性的分析发现,缆索锚头结构可将索身无法测量的超大应变衰减为常规应变测量元件可测的应变,并在此研究基础上,提出了基于锚头内部分布式应变测量的智能索力测量优化方案。同时,通过分析发现,通过对锚头内部分布式应变的信息融合分析,还可实现对锚头内部性能状态的实时监测。然而,锚头作为缆索最为复杂的结构体系,如何实现锚头内部分布式应变的准确测量成为实现上述两大目标的关键。
光纤FBG元件具有应变测量精度高、寿命长、可复用、无电磁干扰、易于温度补偿等显著优点,是植入缆索锚头内部,进行索力测量与锚头状态监测的最理想测量手段[3-4]。然而,由于传感器植入锚头内部位置为非对中位置,其2个维度方向的横向作用力为非对称,由于常规FBG应变传感器中FBG栅区与封装材料直接粘接,被测对象应变直接传递至FBG,FBG元件感受到的将是非对称横向力,由于FBG的光波耦合机理是基于对称横向力作用的前提下推导得出的,如果FBG栅区感受非对称横向应变,会导致FBG反射谱裂变、畸变与剧烈抖动,造成测量值不准确[5-6]。
为此,必须针对锚头内部轴向分布式应变监测方案,研究传感器植入典型位置的非对称横向作用力对FBG反射光谱的影响,评估常规FBG传感器适用性,这既是智能型索力测量方案实现的关键,也是促进其工程实用的关键推动力。
1 锚头内部轴向分布式应变监测方案
斜拉索是承受大跨度结构自重及荷载的关键构件,它主要由索体(包含索身与连接筒)、锚头2部分组成,如图1所示。

图1 斜拉索基本结构体系
锚头作为缆索与大跨度结构的受力连接点,是斜拉索结构最为复杂的承力结构。锚头内部索身钢丝在锚杯内呈放射状散开,穿过定位板上对应的孔眼,并通过墩头定位,锚杯安装后,灌注特制环氧填充料对锚杯中的空隙进行填充。环氧固化后,钢丝、锚固料和锚杯结合成为一个整体。
将斜拉索锚头材料的实际特性参数代入锚头钢丝应力衰减本构模型,其钢丝应变衰减理论公式[7]为
(1)
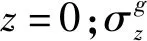
钢丝应力衰减仿真结果如图2所示。
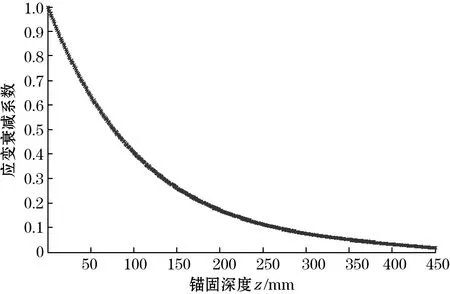
图2 锚头内沿轴线方向的钢丝应力分布
为了实现锚头内部分布式应变的准确测量,且不对锚头的制作工艺产生重大影响,提出了图3所示的分布式应变监测方案。锚头冷铸锚前,将预制好的条状FBG应变传感器通过锚头底部分丝底板预留孔插入缆索锚头钢丝间的空隙处,然后灌注锚固填充料,并进行密实振动,利用锚固填料的固化粘接力,将植入式应变传感器、锚固填充料、钢丝固结为一个整体,从而保证应变传感器能够准确感知由钢丝传递的应变。
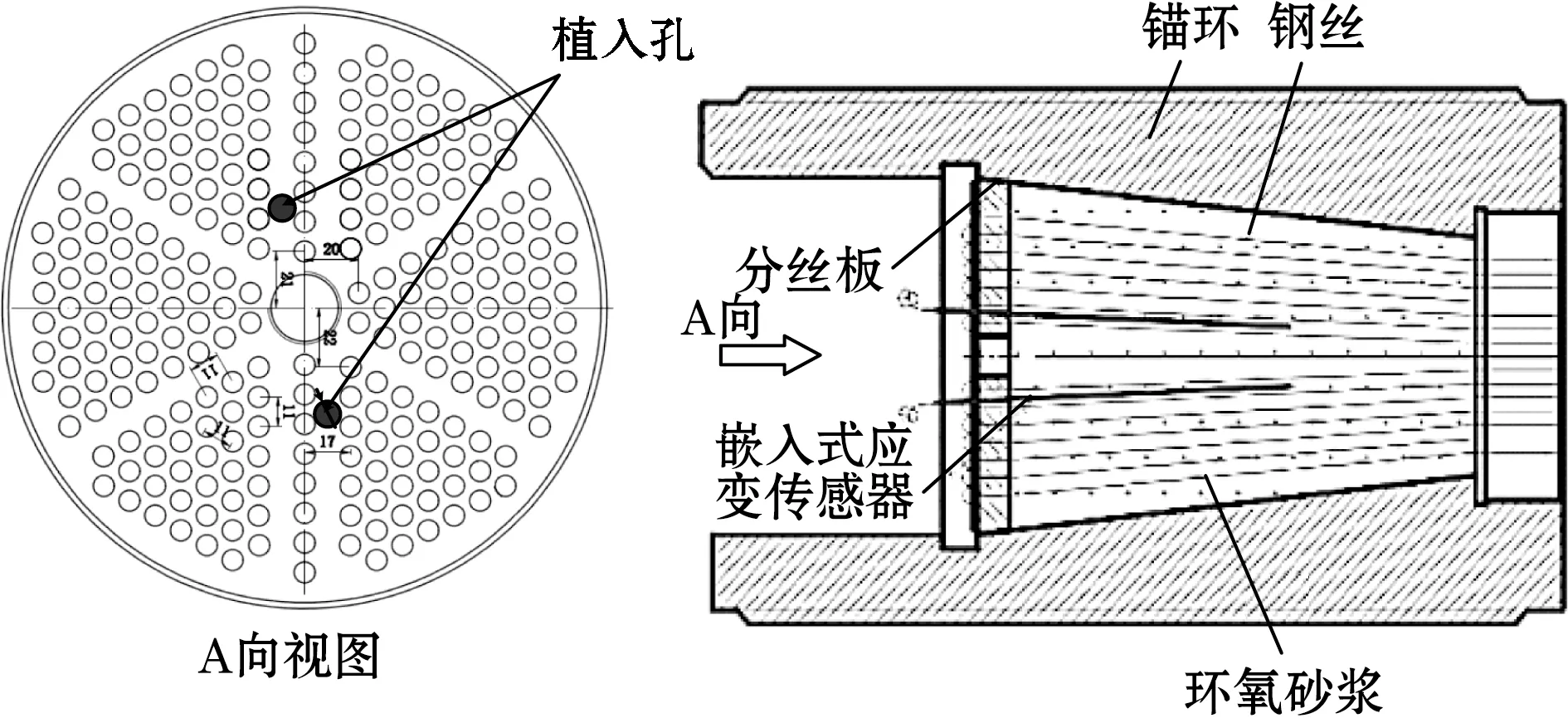
图3 基于锚固区应变测量的索力测量方案
2 横向均匀作用力对FBG传感性能的影响
光纤光栅传感器预植入缆索锚固区后,由于其并非植于缆索锚固区轴心位置,所以其x、y方向受力不等,存在横向作用力作用。在光纤光栅10 mm栅距范围内,其横向作用力可近似为均匀的。为此,将光纤光栅栅区横向受力简化为均匀作用力。
光纤光栅横向均匀受力的示意图如图4所示。光纤直径为D,线芯直径为2a,光栅长度L,栅距为Λ。光纤光栅横向均匀受力为F。
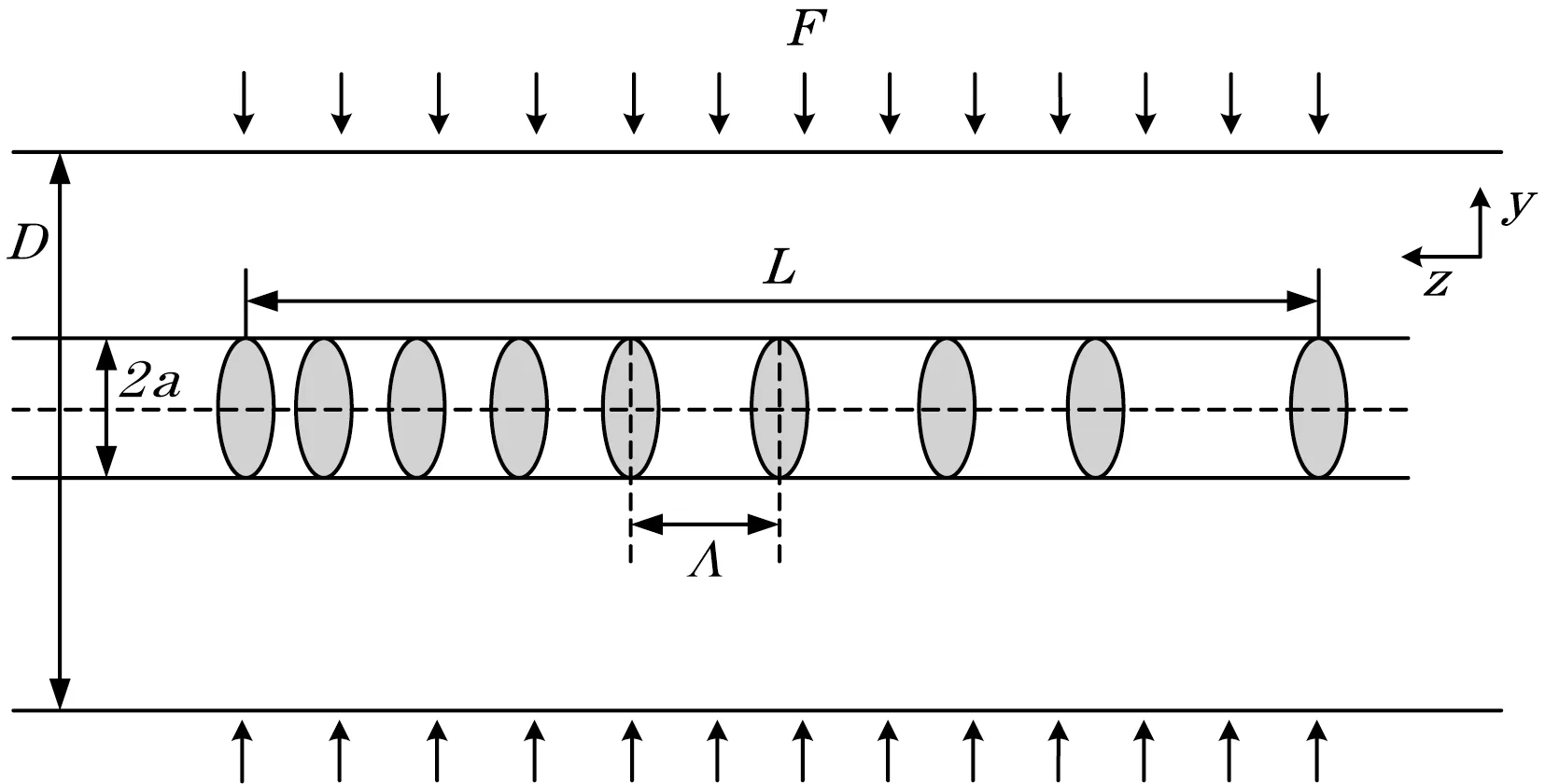
图4 光纤光栅横向受均匀作用力结构图
当沿光纤光栅径向施加作用力时,光纤横截面的受力如图5所示。

图5 光纤光栅横向受力截面图

(1)
(2)
式中:D为光纤直径;F为光纤光栅横向受力;L为光纤光栅长度。
由于光纤纤芯直径远小于光纤直径,所以光纤光栅横向应力可以近似为(x,y)=(0,0)点处的应力。将x=0、y=0代入上式,可得
(3)
(4)
假设光纤光栅的轴向应力为σz,可得光纤光栅的各项应变为
(5)
式中:E为光纤材料的弹性模量;ν为泊松系数。
根据光弹效应原理,结合式(5)可得到光纤光栅的各项折射率变化为
(6)
式中:p11、p12为光纤材料的光弹系数;neff为光纤光栅初始有效折射率。
由式(6)可知,因为σx≠σy,导致x方向的折射率变化量与y方向的折射率变化量不相等,产生双折射现象,使得光纤光栅的反射谱分裂为具有2个中心波长的反射谱。在横向均匀作用力下,光纤光栅2个偏振方向的中心波长变化关系式为:
(7)
(8)
式中λB为光纤光栅初始中心波长。
3 锚固区横向应变分布状态分析
以《大跨度斜拉桥平行钢丝斜拉索》JT775—2010中LMLPES7-211型的实际锚头为分析计算对象,该锚头有211根钢丝。利用ABAQUS软件建立其全尺度三维有限元分析模型,其中钢丝采用梁单元模拟,锚固填充材料采用实体单元模拟,具体如图6所示。

图6 缆索锚固区三维有限元模型
LMLPES7-211型锚头整体有限元网格划分模型如图7所示,共计139 298个单元组成,分别由16 478个B31线性钢丝梁单元和122 820个C3D8R三维实体减缩积分六面体单元组成。锚头的拉拔过程属于稳态过程,且不存在复杂的接触问题,具有无条件稳定性,因此选用ABAQUS/Standard隐式静力求解器进行有限元方程的求解。

图7 缆索锚固区三维有限元网格模型
如图7所示,由于锚杯为锥形结构,当钢丝受拉时,不仅受到轴向拉应力作用,还会受到锚杯内壁传递至钢丝的横向压力作用。锚固区起始端钢丝应力设定为钢丝最大工作设计应力796.5 MPa时,锚固区中锚固深度为10、15、20 cm时典型横剖面处横向应力计算结果如图8所示。
由图8分析可得锚固深度为10、15、20 cm典型横剖面处传感器x、y方向应力分别为:
σx=0.377、0.278、0.098 MPa
σy=0.597、0.374、0.119 MPa
4 锚固区典型位置横向作用力对FBG应力双折射的影响
设光纤光栅的各个参数分别为:E=74.52 GPa,ν=0.17,p11=0.121,p12=0.27,D=125 μm,L=10 mm,λB=1 551.555,x偏振分量与y偏振分量振幅比值为1∶1。根据分析所得的3个典型位置的传感器横向受力数据代入式(7)、式(8),可得横向作用力对光纤光栅应力双折射的影响效果,见表1。

表1 横向作用力对FBG应力双折射的影响
由表1可见,锚固深度为10、15、20 cm 3个典型位置的传感器在横向力作用下,FBG径向x,y2个方向均发生一定的折射率变化,由于2个方向的应力大小不同,折射率变化存在一定差异,产生较小的应力双折射现象。通过进一步分析计算,锚固深度为10、15、20 cm 3个典型位置FBG径向x,y2个方向的波长差值分别为-0.845 56 、-0.368 97、-0.080 71 pm,均小于1 pm。同时,通过分析图9中FBG输出光谱可见,锥形锚杯横向作用力对FBG应力双折射的影响较小,基本可忽略不计。

(a)锚固深度10 cm
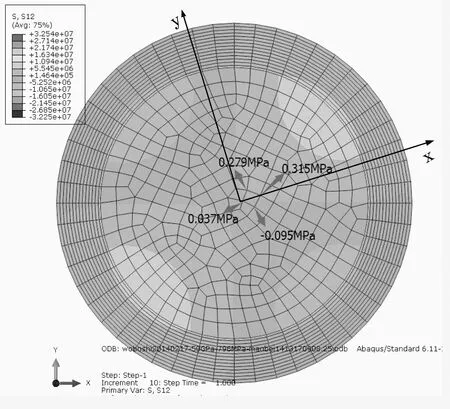
(b)锚固深度15 cm
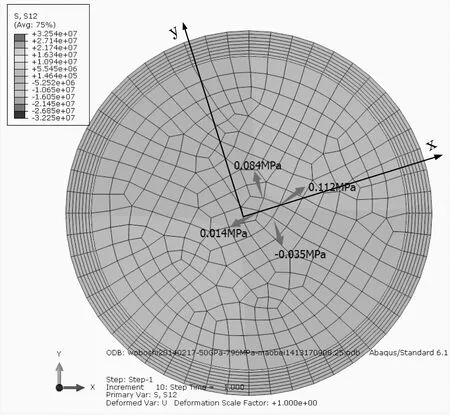
(c)锚固深度20 cm图8 锚头内横向应力力分布图
5 结论
根据推导的横向力作用理论模型,并结合有限元数值模拟实验结果,仿真分析了不同锚固深度横向作用力对FBG传感器性能的影响,分析发现由于2个方向的应力大小不同,虽产生较小的应力双折射现象,但FBG径向x,y2个方向的波长差值均小于1pm,且输出光谱也未出现裂变、抖动的情况,说明锥形锚杯横向作用力对FBG应力双折射的影响较小,可不考虑其影响。
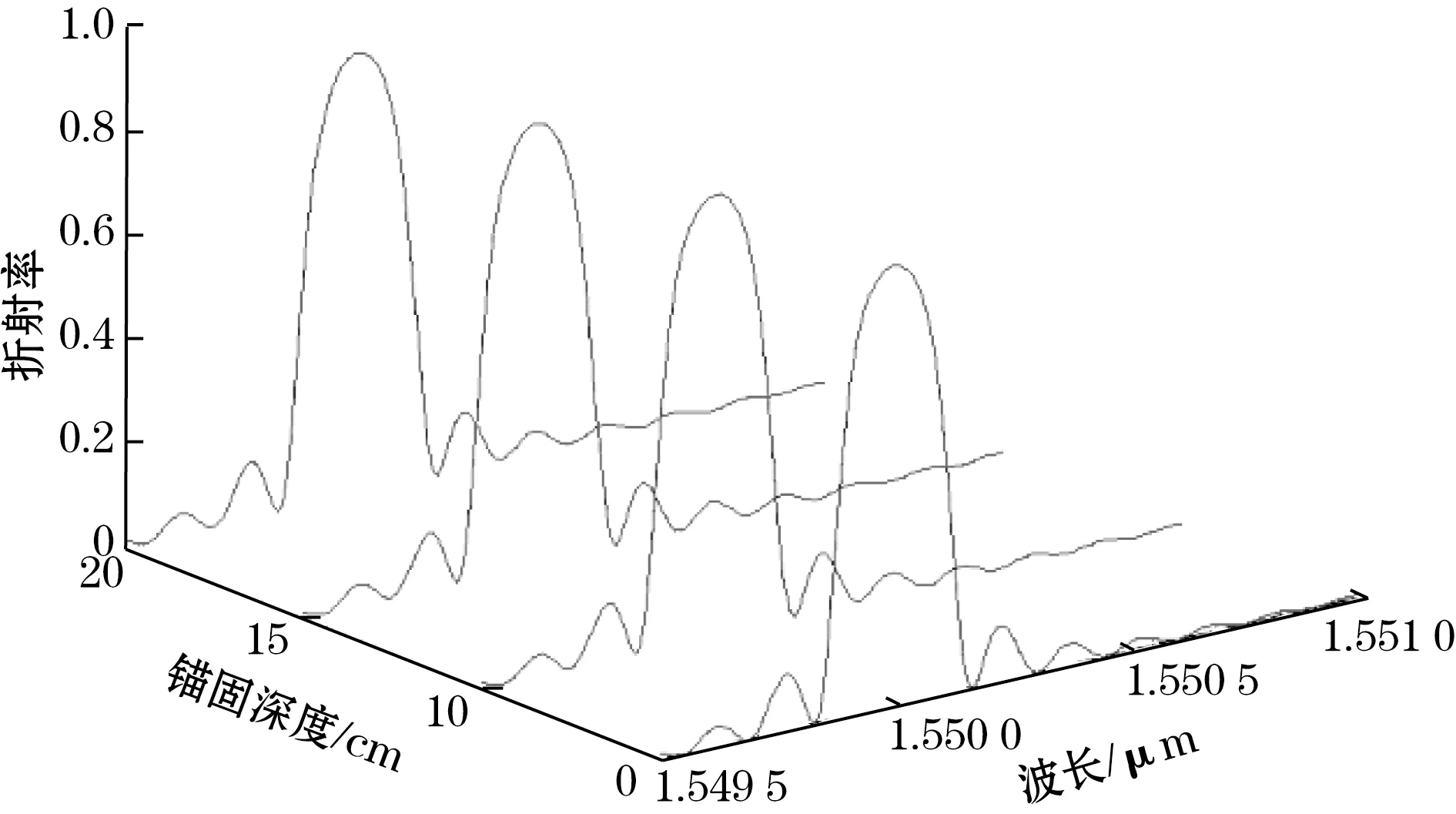
图9 横向作用力对FBG输出光谱的影响

