极区机载SINS/CNS组合导航算法研究*
宋丽君,段中兴,赵万良,成宇翔,付强文
(1.西安建筑科技大学信息与控制工程学院,西安 710055;2.上海航天控制技术研究所,上海 201109; 3.西北工业大学自动化学院,西安 710072)
随着科学技术的发展和国际政治经济军事形势的变化,极区的能源、航运、科研及军事价值日渐凸显,各国在极区的活动日趋频繁,中国的极区事业也开始了以习近平同志为核心的新航程。《关于第十三个五年规划的纲要》中提出要“积极参与网络、深海、极地、空天等新领域国际规则制定”,指出中国要认识极地、利用极地、保护极地,为人类和平利用极地做出新贡献,积极参与极地战略新疆域的国际治理。
由于极区、极区周边以及我国近极区北部边疆领域“两高两低三复杂”(两高:纬度高,海拔高;两低:气温低,气压低;三复杂:物理地形复杂,气候环境复杂,边界分布复杂)的特殊情况,现有的多种导航设备在极区巡航时可靠性和安全性问题一直未得到有效解决,尤其是使用非极区导航方法不能满足极区导航的性能要求[1-2]。
1989年郭洪贵在文献[3]中论述在南极高纬度地区有时能同时见到太阳、月亮和金星等恒星,因此设计了包括太阳、金星、火星、木星、土星及21颗航用亮星在内的一种天文测定方法,白天可以进行太阳移线定位、太阳金星定位,晨昏朦影时观测二星或三星进行定位,该方法为全球天文观测提供了理论依据。
随后国内很多学者也对现有的多种导航方法在极区使用的局限性进行了分析。如2006年王有隆在文献[4]中介绍了北极地区上空飞行时地空通信和导航的特殊性,建议通过提高通信卫星性能和发展多导航系统来改善极区飞行通信和导航条件;2016年杨元喜在文献[5]中客观地分析北极地区卫星导航定位需求,同时分析了GPS/BDS融合导航在极区的覆盖情况,分析了极区导航定位面临的挑战,为未来构建合理优化的极区导航定位方案提供理论基础。
虽然惯性导航系统被认为是极区巡航首选的自主式导航设备,但是惯性导航系统本身具有误差随时间积累的局限性,仅仅依靠惯性导航系统很难完成高精度、长航时巡航功能。因此,极区导航迫切需要引入外部参考信息与惯性导航系统组合进行数据融合修正[6-7]。
组合导航系统的发展是容错组合导航系统和智能导航系统,具有故障检测、诊断、隔离和系统重构的功能,并利用现代最优估计理论、智能信息融合理论等将多传感器、多模式工作方式、滤波及智能计算技术、自动控制系统理论结合为一个整体,形成多功能、多模式、集成化的特点。空天航行惯导算法同地球近地惯导算法相比有许多相近之处,强调利用恒星或其他星体敏感器实现空天、星际飞行器的姿态控制。随着星光探测设备,星光天空背景信噪比技术的不断改进,进一步推进了惯性/天文组合导航系统的发展[8-9]。
1 中低纬度地区SINS/CNS组合导航
天文导航(Celestial Navigation System,CNS)是以不可毁灭的自然天体为导航信标。采用星体敏感器探测恒星星图来确定载机相对于惯性坐标系的姿态,其姿态敏感测量精度非常高,但CNS的姿态更新速率低,且不能提供载机速度和位置的实时信息。SINS/CNS组合导航是利用天文导航系统定期刷新高精度姿态信息来修正SINS随时间不断增长的定姿误差,取长补短,有效提高组合导航系统的测量精度[10]。
1.1 SINS/CNS组合导航原理
本文采用将星体敏感器光轴与载机固联的全捷联模式[11]。SINS/CNS组合导航系统中惯性导航系统通过惯导解算给出载机的三轴姿态信息,星体敏感器也会输出惯性坐标系相对于星体敏感器坐标系的变换矩阵,其组合解算过程如下:
首先,利用SINS输出的载机位置和姿态信息计算出惯性坐标系相对于载机坐标系的变换矩阵;然后,将SINS解算出的变换矩阵与星体敏感器输出的变换矩阵相减作为量测,送入组合导航卡尔曼滤波器进行信息融合,以获得组合导航系统误差的最优估计值,并利用该估计值实时地对SINS进行误差校正;最后,将经过SINS校正的导航参数作为组合导航系统的输出。SINS/CNS组合导航的结构图如图1所示。
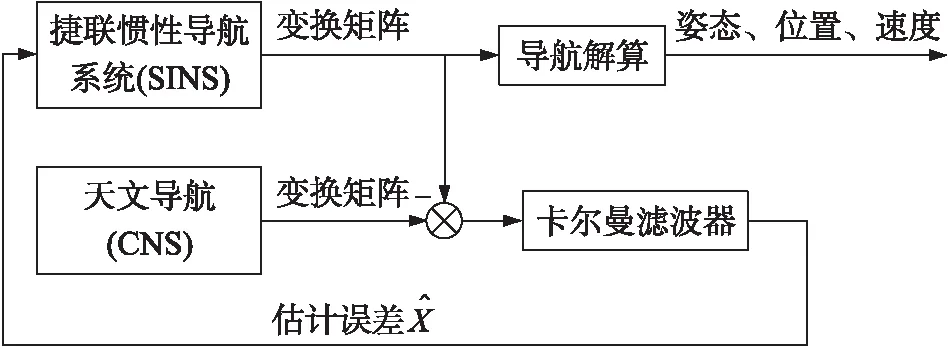
图1 SINS/CNS组合导航结构图
1.2 中低纬度地区SINS/CNS组合状态空间模型

其中姿态误差Cw可以视为Gauss白噪声:
Cw中各项满足条件:

其中,
则
其中,
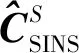
δλ和δL为赤经差和赤纬差,一般是数量级为角秒的小角度,因此可以忽略经纬度影响,即[δP×]=03×3,由此可简化得到:
令
整理可得:
1.3 中低纬度地区SINS/CNS组合仿真分析
中低纬度地区SINS/CNS组合导航系统仿真中设置飞行时间为600 s,SINS的姿态更新、速度更新和位置更新周期均设计为20 ms,惯性器件(陀螺和加速度计)的采样周期设计为10 ms。整个仿真过程中设置器件参数如下。
①初始导航误差
初始姿态误差:[0.5′ 0.5′ 20′];初始速度误差:[0.01 0.01 0.01]m/s;初始位置误差:[20 20 20]m。
②惯性器件性能参数

③星跟踪器性能参数
水平测角精度:10″;方位测角精度:20″;星跟踪器与惯导体系间的安装偏差角误差为[3′,3′,3′]T。

图2 中低纬度地区SINS/CNS组合五种误差
器件参数与高纬度地区飞行器件参数相同,不作修改。仿真结果如图2所示。
①图2(a)是中低纬度地区SINS/CNS组合导航系统得到的姿态误差曲线,由于在SINS/CNS组合导航系统中CNS直接将姿态作为观测信息,而且由于CNS的引入加速了姿态角收敛速度,有效的提高了SINS/CNS组合导航系统的测量精度。所以姿态误差曲线收敛迅速并且精度较高,数秒后姿态误差即达到0.15角分量级。
②图2(b)和图2(c)是中低纬度地区SINS/CNS组合得到的速度误差曲线和位置误差曲线。由图可知,SINS/CNS组合对速度误差、位置误差的估计是发散,这是由于CNS原本就无法提供载机速度和位置的实时信息,因此 SINS/CNS组合对速度误差、位置误差的估计发散。
③中低纬度地区SINS/CNS组合对陀螺常值漂移、加速度计常值偏置的估计误差曲线见图2(d)和图2(e)。组合系统定位误差的主要误差源为水平姿态误差角,方位姿态误差角相对来说影响较弱。而在惯导系统给出的姿态信息中,陀螺常值漂移直接对姿态误差角产生影响。SINS/CNS组合导航系统对陀螺常值漂移、相关漂移的估计较好,对加速度计常值偏置的估计发散。
2 基于格网框架的极区SINS/CNS组合导航算法
为避免航向参考线在极点处收敛,在极区航图上将所有的经线平行于格林威治子午线绘制,这样载机的方位测量就是相对格林威治子午线及其平行线定义,即格网导航。关于格网坐标系以及格网导航力学编排在已在本文作者文献[14]中进行过详细描述,这里不再赘述。
2.1 格网方位与真北方位间的关系
任何导航系统在高纬度地区都会因为极区经线收敛造成以真北作为航向参考的困难。在惯性导航中,中低纬度地区采用指北方位惯导力学编排方案,航向以真北作为参考,与之对应的天文导航系统也以真北向作为航向参考;而在高纬度地区为克服经线收敛造成的定位定向难题,惯导系统采用格网力学编排方案,与之对应天文导航系统也应以格网北向作为航向参考[15-16]。
此外,格网惯性导航系统的位置信息可以直接与极区航图相匹配,只需在极区球面投影航图上叠加格网线即可实现。因为格网线平行于格林威治子午线,所以飞机飞行所在地的经度和所用航图的收敛因子(Convergence factor,CF)决定格网北向(GN)和真北(TN)向间的夹角。
北半球:
格网方位=真北方位+经度(W)×收敛因子
格网方位=真北方位-经度(E)×收敛因子
南半球:
格网方位=真北方位-经度(W)×收敛因子
格网方位=真北方位+经度(E)×收敛因子
2.2 极区SINS/CNS组合导航系统状态空间模型
在极区SINS/CNS组合导航中,不仅考虑SINS的误差源,同时考虑到星体敏感器光轴与载机固联,因此需要将SINS和星体敏感器间的安装偏差角也列入状态变量,选取SINS/CNS组合导航系统的状态变量为:惯导平台失准角φ=[φGEφGNφGU]T,分别为惯导平台的格网东向失准角、格网北向失准角和格网方位失准角;惯导速度误差δvG=[δvGEδvGNδvGU]T,分别为惯导的格网东向速度误差、格网北向速度误差和格网天向速度误差;惯导位置误差δRe=[δxδyδzT,分别为ECEF坐标系下的x向、y向和z向位置误差;陀螺随机常值漂移ε=[εxεyεz]T,分别为x向、y向和z向陀螺随机常值漂移;加速度计随机常值偏置=[xyz]T,分别为x向、y向和z向加表随机常值偏置;惯导体系和星跟踪器体系间的安装偏差角μ=[μxμyμz]T分别为x向、y向和z向安装偏差角。因此惯性/天文组合导航的系统状态向量XC为:
XC=[φGE,φGN,φGU,δvGE,δvGN,δvGUδx,δy,δz,εx,εy,εz,x,y,z,μx,μy,μz]T
(7)
结合格网SINS导航误差方程和格网SINS/CNS组合导航系统的状态XC可列写出组合导航的状态空间模型:
其中
极区SINS/CNS组合导航的量测量选取为SINS计算得到的变换矩阵与星体敏感器输出的变换矩阵的差值,结合极区SINS/CNS组合导航状态空间模型,建立极区SINS/CNS组合导航的量测模型。
极区SINS/CNS组合导航系统量测模型为:

2.3 极区SINS/CNS组合导航仿真轨迹
极区SINS/CNS组合导航系统仿真中设置飞机飞行6 h,轨迹如图3所示,整个飞行过程中模拟了飞机的加速、爬升、转弯机动。
轨迹参数:轨迹起始点:[45°N108°E 500 m];轨迹纬度最高点:89.26°N;飞行速度:起始速度0 m/s;最高速度310 m/s。

图3 极区SINS/CNS组合仿真三种情况
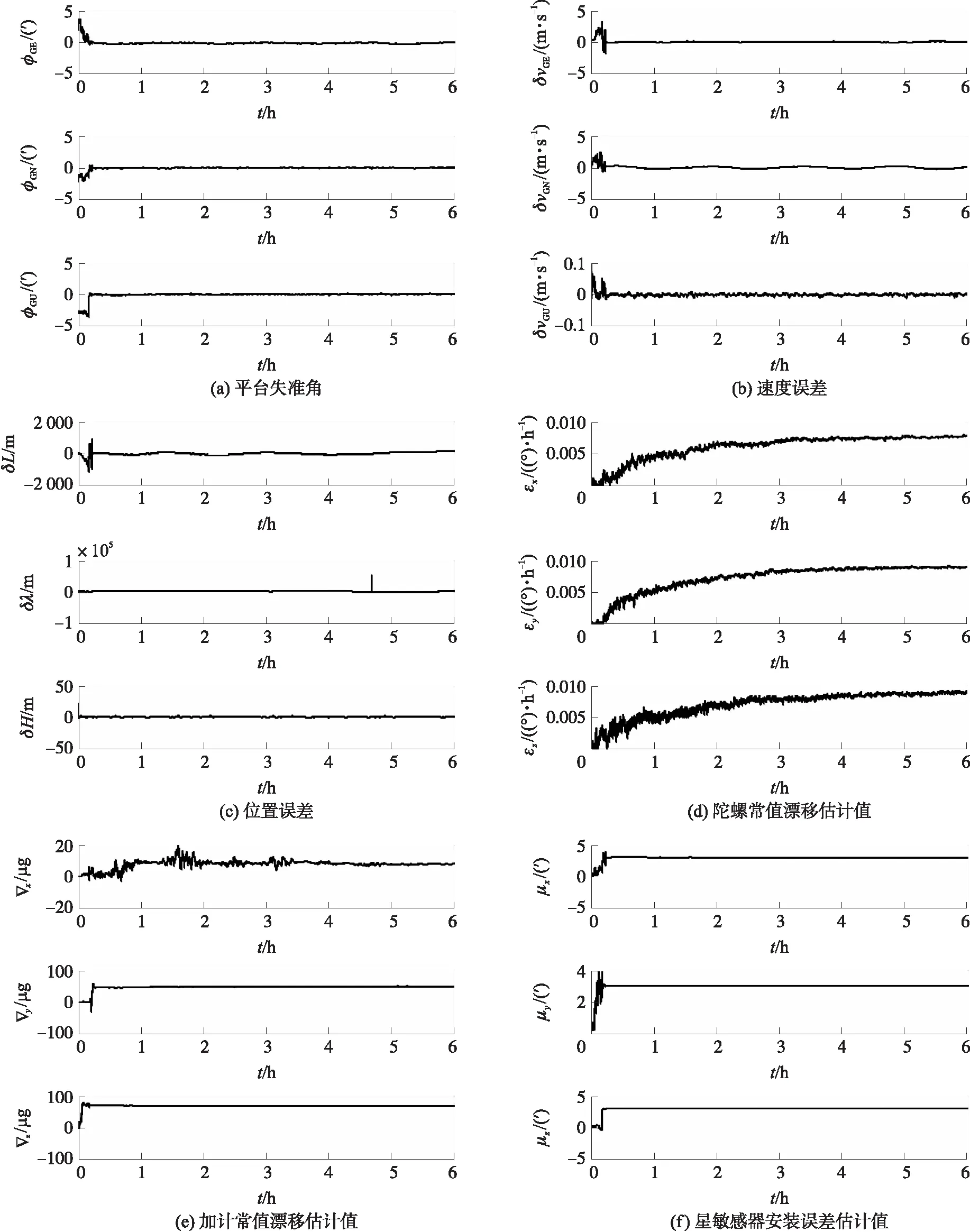
图4 极区SINS/CNS组合仿真六种情况
2.4 极区SINS/CNS组合导航算法仿真
整个仿真过程中设置器件参数与中低纬度地区参数相同,只有轨迹发生变化。仿真结果如图4所示。
①极区SINS/CNS组合平台失准角如图4(a)所示,平台失准角基本在100s内收敛到0.5′之内,与中低纬度地区SINS/CNS组合导航系统得到的姿态误差曲线基本一致。
②极区SINS/CNS组合平台速度误差和位置误差如图4(b)和4(c)所示,速度误差以舒拉振荡周期振荡,稳定后的速度振荡最大幅值不超过0.5 m/s。位置误差同速度误差对应,也呈舒拉振荡的形式,振幅小于30 m。
③极区SINS/CNS组合陀螺常值漂移估计值和加计常值漂移估计值如图4(d)和4(e)所示,随着陀螺漂移和加速度计零偏逐渐被估计,速度和位置误差的幅值也逐渐减小。
④星敏感器安装误差角如图4(f)所示,安装误差角的估计速度与平台失准角的估计速度一致,最终安装误差角估计收敛至。
3 结论
基于格网框架的极区SINS/CNS组合导航算法是在格网坐标系进行惯性力学编排以克服经线收敛引起载机定位定向困难的问题。本文结合SINS格网导航误差模型和选取的极区SINS/CNS组合导航系统的状态变量,建立格网框架下极区SINS/CNS组合导航的状态空间模型。由仿真结果可知,极区SINS/CNS组合导航不仅有效抑制了陀螺漂移引起的误差,还及时修正了系统输出的各项导航参数。在惯性元器件精度相同的条件下,极区SINS/CNS组合导航与中低纬度地区SINS/CNS组合导航精度基本一致。

