基于相场法熔盐相变的模拟研究

王超颖，顾璠

（东南大学能源与环境学院，江苏南京 210018）

0 引言

利用相变蓄能技术可对不连续、不稳定的热量进行充分利用，有效提高能源利用效率[1]，在太阳能热利用[2]、工业余热回收[3]、建筑节能等领域中相变材料都有着诱人的应用前景。陈思等[4]比较了不同的蓄热热泵，得出制冷剂化霜时先流过热交换器再流过蓄热器更合理的结论；王聪等[5]研制了一种新型的管肋式相变蓄冷换热器，经测试蓄冷器的 平均功率为4,057.2 W，为太阳能空调实验系统提供了设计依据。KALAISELVAM等[6]研究了相变材料在柱状密封体中完全相变所用的时间，通过模拟和实验对比可知完全凝固时间依赖于Stefan数和生成热参数，完全熔化时间依赖于当量导热系数，模拟熔化过程比凝固过程更接近实验结果。由于熔盐材料在蓄热技术中的广泛应用，本文拟用相场法模拟计算其相变过程。

相场法基于Ginzburg-Landau相变理论[7]，采用扩散界面模型，认为两相界面有一定厚度，各种传输现象均通过该界面区域完成。以熔化过程为例，固相、液相和界面作为不同的相态用体积分数来跟踪系统中的相，无需追踪界面将固液相分开处理，因此在整个求解域中均采用相同的数值计算方法。相场法早期用于枝晶生长的研究[8]，BECKERMANN等[9]用一种相场模型模拟了凝固过程中的微观结构变化，如今，相场法已成为许多领域一种重要的研究方法[10-11]。

1 计算方法与验证

1.1 理论模型

相场法用相场变量Φ表示系统时间和空间上的物理状态。在本文的计算中，Φ的值代表了液态或固态，Φ=1表示固态，Φ=-1表示液态，-1＜Φ＜1代表相界面。

流体的速度场和压力场通过不可压N-S方程表示[12-13]：

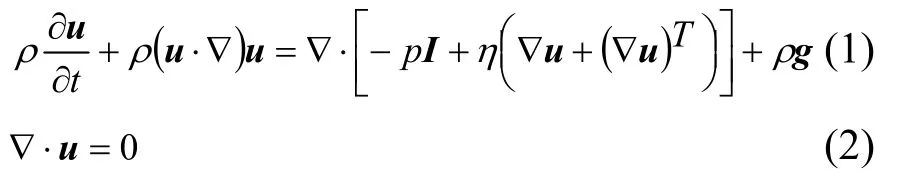
对相场变量的处理方程[14]：

通过相界面的质量(相变速率)计算如下[15]：

连续性方程考虑相变后变更如下：

式中：F为体系自由能；γ为迁移率；λ为混合能量密度；ΔHl为熔化焓。

1.2 相方程用于液固相变计算的讨论

假定初始物理场温度一致，处于相变温度，考虑重力。流动中，认为边界无滑移。图1为二维等压流动过程入口流体速度积分，可知当黏性系数大于1 Pa·s时，速度极缓且趋于稳定，在之后的相变计算中，固相的黏度取1 Pa·s。

图1 二维等压流动过程入口流体速度积分

1.3 验证计算

本文查阅已有的实验结果[16]，模拟计算来验证计算模型的可靠性。石蜡物性如下：石蜡的熔点为41.98 ℃，相变潜热为141 kJ/kg，导热系数为0.2 W/(m·K)，比热为2.0 kJ/(kg·K)，液态密度为800 kg/m3，固态密度为916 kg/m3，液体运动黏度为5×10-6m2/s。

验证计算模拟了石蜡在方形蓄热槽中的相变过程，蓄热槽中心有一圆管，管内提供60 ℃的恒温水，石蜡分布在管外，水与石蜡通过管壁完成换热，方形槽边长为10 cm，圆管直径为2 cm。

图2为石蜡测点分布，上测点1#到管中心距离为1.5 cm，下测点2#到管中心距离为4.5 cm。图3为蓄热槽的结构。为了简化计算模型假设：管壁材料的导热系数很大，管壁厚度可视为零，管壁内侧与外侧温度相等；相变材料在相变时不发生过冷和过热现象；流动为二维，非稳态，层流，蓄热槽没有漏热损失，即蓄热槽上下左右表面绝热。

图2 石蜡测点分布

图3 蓄热槽的结构

图4为上测点和下测点温度的对比。蓄热槽内，上测点处的相变材料温度上升迅速，在短时间内完成相变并达到稳定状态，且上部液态区形成了自然对流加快了传热速度；下测点处的相变材料温度变化缓慢，在300 min内都没有达到相变温度，一是因为石蜡导热系数较小，二是因为下部区域传热方式为导热。从文献中的实验温度值与本研究的模拟温度值对比结果可看出，对初始温度的假设并不影响最终结果，模拟与实验达到稳定相变的时间相近，最终温度吻合良好，验证了相场模型计算的可靠性。

图4 上测点和下测点温度的对比

2 二元系液固相变模拟和特性分析

由于石蜡蓄热能力较小，选取混合盐作进一步的研究。混合盐经适当改变其组分的配比可得到希望的熔点，温度适用范围更广，将储热性能好的高价格物质与低价格物质合在一起使用可节省成本[17]。综合经济因素与导热性能，本文选用了NaCl-CaCl2作为相变材料，研究高温熔盐的相变特点。图5为某实验的NaCl-CaCl2二元相图[18]，当NaCl的摩尔占比约为50%时，体系的共晶温度为773 K。

混合工质物性按摩尔比计算，工质物性参数如下[19-20]：二元系的共熔点为773 K，相变潜热为377.303 kJ/kg，导热系数为2.61 W/(m∙K)，比热为1.07 kJ/(kg·K)，液态密度值为1,861 kg/m3，固态密度值为2,159.6 kg/m3，液体运动黏度为1.2×10-6m2/s。利用上一节介绍的模型，初始温度为相变温度，模拟材料在不同结构、不同壁温下的熔化过程。

图5 氯化钠与氯化钙二元相图

2.1 液固相空间分布与传热特性

对蓄热槽内熔盐的熔化过程进行模拟，管内提供1,200 K的恒温热源，分别得到管壁热流密度和相界面长度的变化曲线（图6～图7）。

图6 管壁热流密度变化曲线

图7 相界面长度变化曲线

热量从管壁往四周辐射，随着周围温度上升，温差变小，且随着相变的进行，液相增多，相界面长度（固液接触长度）不断变长，至26 s时达到最大，同时相变热大量积聚。管壁热流量的值开始时特别高，原因是管壁与很薄的液体层接触，温差很大，热阻很小；随着相变进行，管壁周围液体层逐渐变厚，传热热阻变大，热流量持续减小；在30 s附近热流量增大，是因为上部液体层出现自然对流，加快了热量传递，此时相变区域覆盖到将近整个区域的一半。而后由于固相变少，固液接触减少，界面长度不断缩短。当上部区域基本熔化、传热向下方扩散时，相界面发生变化，下方的低温区传热方式为导热，熔化缓慢，热流密度保持降低趋势直到熔化完成。

2.2 不同壁温对比

图8为圆管内测点分布，外管径为4 cm，内管径为1 cm，上部测点距圆管中心0.8 cm，下部测点距圆管中心1 cm。图9为上测点和下测点温度变化图，由图9可知，当壁温Tw=1,400 K时，圆管上部分相变材料温度迅速升高，在短时间内达到一个相对稳定的传热过程，壁温1,200 K相对1,400 K温度升高慢，但趋势类似，都是在短时间内有一个较大的升温，Tw=1,000 K时，斜率比较低，温度上升比较慢。而圆管下部分熔化速度缓慢，经过60 s，1,400 K壁温下的该测点材料才开始熔化，Tw=1,200 K时用了90 s，而Tw=1,000 K时，在120 s之前几乎没有开始熔化。综上所述，上部区域形成对流，传热速度快，下部传热方式为导热，传热速度慢。因此，在利用相变蓄热的结构中，应注意强化下方区域的传热性能。

2.3 不同结构对比

图10所示为当Tw=1,200 K时，圆管内相分数的变化。由图10可知，开始时的熔化过程主要集中在圆管上部区域。上部区域内的相变材料快速熔化，形成对流，当液相局部布满顶端时，熔化过程向左右两端扩散，形成类似折扇的图案，而后向下方继续扩展开来。但侧面熔化完成后，熔化速度减慢，此时的传热方式为导热，在下方区域的熔化过程（时间几乎为上方熔化时间的两倍）中，由于表面张力的影响，相变材料沿着管壁在圆管底部形成凸起，最终慢慢熔尽。

图8 圆管内测点分布

图9 上测点和下测点温度的变化

图10 圆管内相分数的变化（Tw=1,200 K）

图11为相同壁温下方管内的相分数变化，方管与圆管的熔化过程略有不同，方管耗时时间短。一方面，外管周长相同，圆管相对于方管传热面积大，所需的熔化时间更长。另一方面，由于形状不同，方管内的熔化过程受到的表面张力影响比较小，虽然熔化至相界面将近水平时耗时相近（约40 s），但熔化后期方管内的传热面积基本保持不变，传热速率稳定；而圆管内壁面效应积聚，底部固相区迟迟难以熔化，传热速率极大地减小。

图11 方管内相分数的变化（Tw=1,200 K）

3 结论

本文模拟了石蜡的熔化过程并将其与文献中的实验结果对比，验证了相场模型用于液固两相流相变计算的可靠性。研究了二元相变材料NaCl-CaCl2在圆形与方形蓄热槽内伴有对流传热的蓄热过程，给出了定壁温下熔化过程的固液相图，得到如下结论：

1）壁温越高，熔化越快。相变过程中的传热性能受黏度的影响，黏度增大（黏度大于1 Pa∙s时基本稳定）使相界面更平稳但相应地传热速度会减慢，因此要根据对蓄热过程的要求选择合适的材料；

2）从相界面长度的变化及传热特性的分析可知，熔化前期用时短，因为对流引起传热系数增大，而熔化后期速度慢，传热方式为导热；

3）相同周长的圆管比方管耗时多，且方管受到表面张力的影响比圆管小。