翅片管束大空间自然对流三维数值模拟

马腾飞，王文，叶成，左巧林

（1-上海交通大学制冷与低温研究所，上海 200240；2-上海核工程研究设计院，上海 200233）

0 引言

热管具有极强的导热能力，在制冷和散热中具有广泛应用。为了提高热管的换热能力，通常在热管外部或者内部增加翅片来增加传热面积或者增强空气扰动[1]，这种带翅片的热管称为翅片管。目前平翅片、开缝翅片、螺旋翅片以及百叶窗切口翅片等翅片形式应用较多[2]。

由多支翅片管按一定规律排列起来而组成的传热单元叫翅片管束。翅片管束自然对流散热常用于大型散热系统的非能动冷却[3]，非能动安全系统是指不依赖外界动力输入，依靠自然对流、重力等来实现安全功能的系统，主要功能是保障核电站在事故条件下的安全[4]。例如AP1000的非能动余热排出系统就应用了热管管束来导出堆芯内的热量[5]，如图1所示。

图1 非能动冷却系统

对热管管束换热，有不少学者进行过研究。唐家俊等[6]等实验研究了管排数对管束积灰以及压降的影响。何法江等[7]采用SIMPLE算法的模型对空气横掠翅片管束的流动传热进行了模拟仿真，得到翅片管束的进口空气流速增加时流动的阻力系数减小。陈松等[8]建立了满液式壳管蒸发器壳侧换热模型，在此基础上优化了管束排布方式，使单管平均换热性能提升了13.9%。焦凤等[9]通过实验和仿真计算的方式研究了圆形翅片管束排列方式和管间距等参数对换热性能的影响。陈洁璐等[10]通过Fluent对3种翅片类型的风冷冷凝器局部模型进行了数值模拟，分别得到其传热系数和摩擦因子随进风速度的变化规律。赵夫峰[11]通过数值分析研究了翅片厚度对不同结构的翅片管换热器性能的影响。

当模型尺寸较大或者结构太过复杂时，不适合进行实物建模仿真。因此管束仿真的另一种方法是将管束简化为多孔介质进行计算，进而将计算量减小到计算能力允许的范围内。HOOMAN等[12-13]对多孔介质模型进行了较为详细的介绍，并将其应用于空气冷凝器的设计。戈剑等[14]通过将热交换器中的管束区简化为多孔介质对核电站断电5,000 s后的工况进行了计算，并对照实验结果验证了计算方法的正确性。孙世梅等[15]通过引入多孔介质模型对热管换热器压降和温度场分布进行了模拟计算，结果与实验吻合良好。李欣等[16]通过类似的方法对管壳式换热器进行了仿真，得到了换热量随壳侧Re变化的特性曲线。

热量被热管蒸发段吸收后，需经由冷凝段通过自然对流等方式排出，空气流过冷凝段管束时的速度是影响散热能力的重要参数。本文将整个管束简化为多孔介质，分别设置体积热源和面热源两种热边界条件，对热管管束冷凝段的大空间自然对流数值模拟方法进行了研究。

1 简化模型及验证

1.1 多孔介质模型

当翅片管束规模较大或者较复杂时，考虑到网格划分可行性以及计算量，将管束简化为多孔介质。多孔介质模型的基本思想：一个控制体中同时包含流体和固体，通过在流体上附加流动阻力，即在动量守恒方程中添加动量源项来表示固体对流体流动的影响[17]。

多孔介质区域的控制方程见式(1)～式(3)｡ 质量守恒方程：

动量守恒方程：

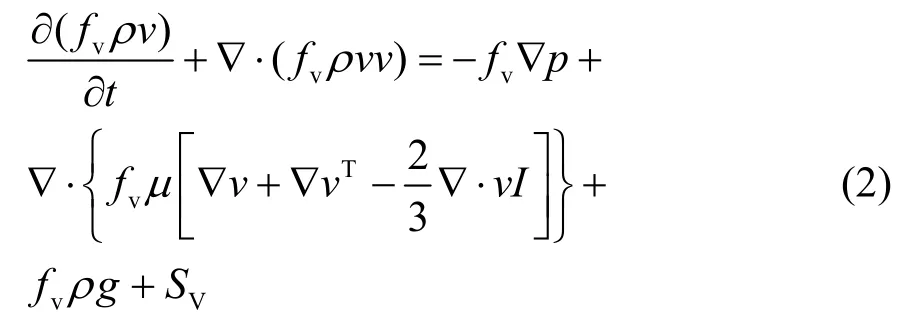
能量守恒方程：

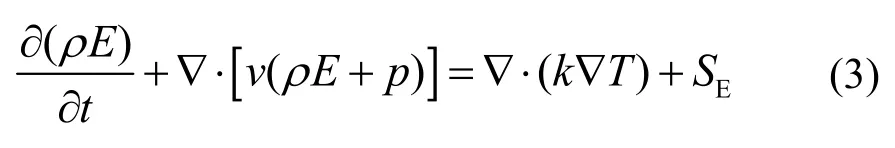
式中：

fv——多孔介质孔隙率；

V——流体速度矢量；

μ——黏度；

Sv——流体流经管束产生的附加阻力，3N/m；

SE——能量源项。

对简化模型的合理性进行验证，采用的方法是对小尺寸小数目的管束进行实物建模仿真，之后再将管束简化为多孔介质，对比两种方法得到的结果的差异。考虑到实物建模的可行性，采用的管束为光管，直径50 mm，长200 mm，管间距为100 mm。采用ICEM CFD进行几何建模和网格划分，图2和图3为实物模型以及简化为多孔介质后的几何网格模型图。经过网格无关性验证，实物模型采用的网格数为156万，而多孔介质模型的网格数为26万，仅仅为前者的17%，极大减小了计算量。

图2 网格模型

图3 介质网格模型

1.2 模型设置

多孔介质模型需要确定其阻力系数，使空气流经多孔介质的阻力与流经管束的阻力相等。因此需要确定空气流经管束的压降与流速的关系，通过CFD计算得到图4。将压降拟合为流速的二次函数，得到：

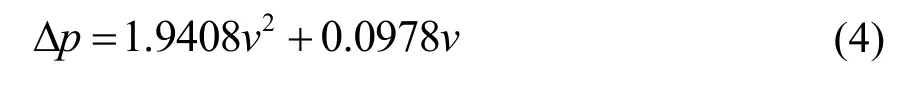
在此关系式的基础上得到多孔介质的阻力系数。

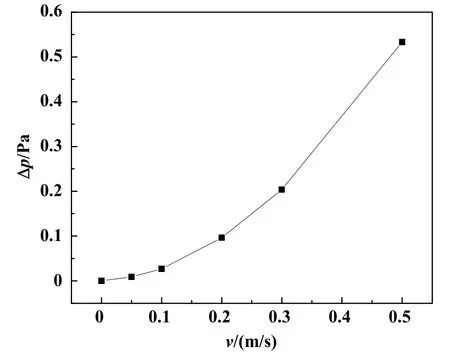
图4 管束压降与流速关系

管束接触的墙壁以及地面设置为绝热壁面，大空间边界设置为压力出口边界条件[18]，通常对翅片管管壁设置为第一类边界条件，即定壁温[19]。将管束简化为多孔介质时，热源加载方式有两种，一种是对多孔介质设置定体积热源，另一种是在管束与壁面交界处设置面热源，如图5所示。两种热源设置方式保证管束向外界空间的散热量相等。由于热管内部为相变换热，当量传热系数很大，因此将多孔介质固体骨架的导热系数设置为一个极大值。比较两种热源设置方式计算得到的结果差异。

为加快收敛，计算采用Boussinesq近似[20]。湍流模型采用在工程中应用较为广泛的κ-ε模型。控制方程采用有限容积法进行离散，压力和速度的耦合采用SIMPLE算法，压力差值格式应用SIMPLE算法的标准格式[21]。

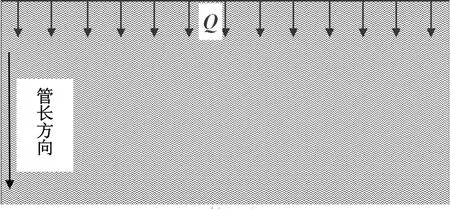
图5 面热源设置

1.3 验证结果

图6 为管束简化前后验证计算结果。由图6可知，管束散热功率越大，周围空气的浮升力也越大，因此空气跨管流速越大。对多孔介质模型设置面热源和体积热源时得到结果基本相同，与管束模型相比相差不足10%，简化模型的精度较高。

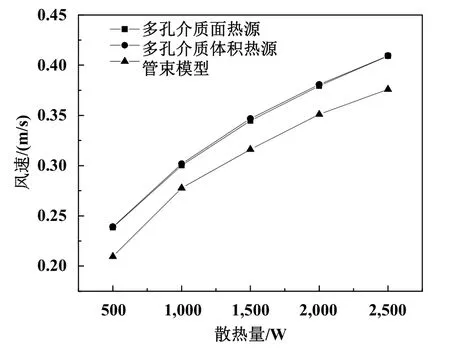
图6 管束简化前后验证计算结果

2 计算模型

证明管束模型简化的合理性之后，对大尺寸的翅片管束进行自然对流仿真计算。计算采用的热管冷凝段的管束形式如图7所示，其中基管直径为76 mm，管长5 m，翅片厚度1 mm，间距5 mm，高15 mm。管束采用叉排形式，管间距为300 mm，共4排，每排有25根热管，最下排距地面3 m。管束从墙壁处穿出，悬置于大空间中，总的散热量为0.25 MW。

图8为简化得到的多孔介质模型，计算域由多孔介质和外界大空间组成，经过网格无关性验证最终采用的网格量为370万。

图7 热管冷凝段的管束形式

图8 多孔介质计算域

流体流经管束的压降采用经验公式[22]：

对叉排管束：

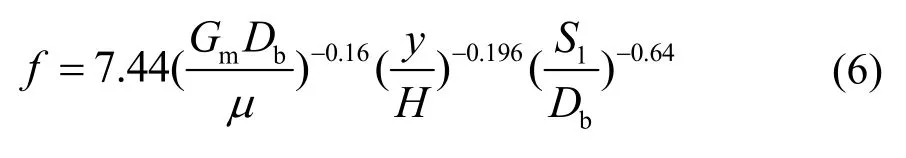
式中：

N——流动方向管排数；

Gm——最窄截面处的质量流量，kg/s；

Db——基管直径，m；

y——翅片间距，m；

H——翅片高度，m；

S1——垂直流动方向的管间距，m。

通过经验公式计算出压降与空气流速关系，在此基础上设置多孔介质阻力系数，模型其余设置与1.2中相同。

3 计算结果与分析

比较两种热源设置方式的计算结果，图9为计算区域整体以及管束上表面温度场云图。可以看出当设置为体积热源时管束区域的温度分布更为均匀，设置为面热源时，靠近发热面的区域温度较高。

图10为面热源情况下计算区域的空气流动形式。可以看出大空间自然对流的流动形态，空气在浮升力的作用下向上流动，在此过程中与管束进行对流换热，左右两侧的空气向中间流动以补充减少的空气。

将管束简化为多孔介质可以减小计算量，但是计算结果无法准确描述管束内部的换热和流动特性，而只能反映整体的空气流速。对于此流速，采用面热源时得到的数值为0.51 m/s，设置体热源时速度为0.52 m/s，可以认为两种热源边界条件计算得到的空气掠管空气流速相等。

图9 计算区域整体以及管束上表面温度场云图

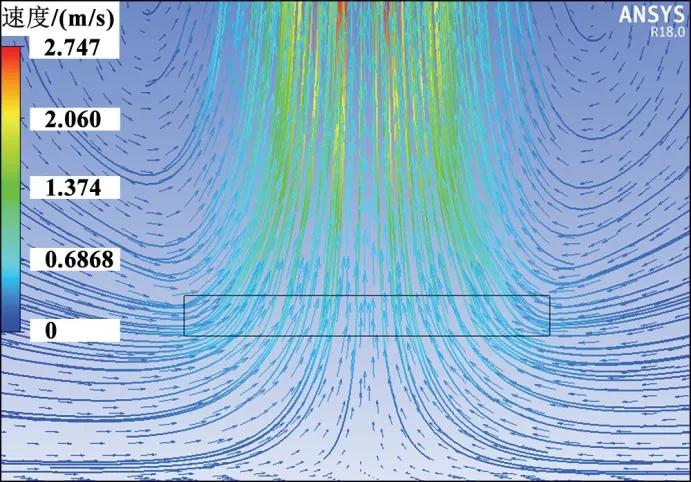
图10 空气流动矢量图（矩形线框代表管束区域）

4 结论

对翅片管束进行大空间自然对流数值模拟时可将管束简化为多孔介质，热源可设置面热源或体积热源。模型简化前后计算得到的掠管风速相差约10%，准确度较高。简化后可在计算机计算能力允许范围内对管束区域的空气流动宏观参数进行模拟计算，为热管换热系统的设计提供数据参考。