基于双预测模型的多联机能耗数据异常诊断策略
李昱瑾,陈焕新,刘江岩
(1-华中科技大学中欧清洁与可再生能源学院,湖北武汉 430074; 2-华中科技大学能源与动力工程学院,湖北武汉 430074)
0 引言
多联机系统由于其能耗低、热舒适性高等优点广泛应用于商场、公寓等场所[1-2]。在能源有限的前提下,保证建筑舒适度的同时,如何有效地降低建筑物空调系统能耗成为一个重要的研究内容。多联机空调系统作为主流空调系统之一,对其能耗进行预测分析,在能源管理、运行策略优化、控制优化等方面都有重要的意义[3]。能耗预测结果的准确度很大程度上受实验数据的可靠性影响,因此,如何查找和剔除原始数据集中存在的不合理数据至关重要。
对于能耗故障数据的剔除问题,可以从以下两个角度来寻求解决办法。一是通过对多联机系统进行故障检测和诊断[4](Fault Detection and Diagnosis,FDD)找出发生故障的传感器或者机组元件并进行更换,从源头上解决采集到故障数据的问题;二是通过对采集到的数据进行统计学分析,排除其中的不合理数据来提高数据的可靠性。
目前,制冷系统故障诊断的方法大致可以分为以下3类[5]:基于定性知识的故障诊断方法;基于解析模型的故障诊断方法;基于数据驱动的故障诊断方法。基于数据驱动处理的方法中,回避了建立准确数学模型的难点,对于线性和非线性系统都具适用性[6]。WANG等[7]首先提出将主元分析法应用于制冷空调行业的故障诊断领域中,诊断效果良好。周镇新等[8]提出了一种基于PCA-Clustering的压缩机回液故障诊断的方法,该方法能够在数据标签未知的情况下,较好区分不同类别的压缩机回液故障及正常数据,使压缩机回液故障诊断率达到94.29%。曾宇柯等[9]针对传统神经网络模型过拟合等问题,提出一种基于改进贝叶斯神经网络的多联机故障诊断策略,该策略使用LOF(Local Outlier Factor)法有效剔除了原始数据中的异常值,并构建了LOF-BR神经网络诊断模型,相较BP(Back Propagation)神经网络诊断性能增强,整体检测率提高至97%。GUO等[10]提出一种卷积主元分析的方法,与传统的主成分分析方法相比,这种方法可以显著地提高多联机系统故障检测及诊断的精度。
数据挖掘技术[11-12]将有效信息和数据规律成功地从海量数据中提取出来,并广泛应用于系统故障诊断问题的相关研究中。但在能耗预测问题的研究中,为了消除可能由于系统传感器等数据采集元件故障引起的异常数据,对系统进行故障诊断并更换元件,再重新采集数据,这显然缺乏效率以及便利。能耗数据的采集通常需要花费很长的一段时间,且数据量庞大,寻求从海量数据中剔除少量的异常数据的方法,才能更加行之有效。
本文利用实验收集到的多联机系统某段时间内连续运行的能耗数据,在箱线图分析的基础上,提出一种基于支持向量机(Support Vector Machines,SVM)和最小二乘支持向量机(Least Squares Support Vector Machines,LS-SVM)能耗预测模型双模型对比分析策略,实现对数据质量的进一步分析和筛选。结果表明该方法有效地提高了数据的可靠性和预测结果的准确性。
1 双模型对比诊断策略
随着统计学习理论[13]的提出,SVM[14-15]分析方法也应运而生。对于有限样本问题的研究,SVM建立了一套完整的、规范的基于统计学的机器学习的理论和方法,很大程度减少了算法设计存在的随意性,克服了传统统计学中期望风险和经验风险之间可能存在较大差别这一缺点[16]。
支持向量回归方法基本思路为:在训练数据集有限的条件下,建立起输入与输出之间连续的函数关系,使预测误差尽可能小并尽可能保证回归函数的平滑性。
1.1 支持向量机(SVM)
对于本文的多联机系统,支持向量回归问题可以描述为:对于实验获得的多联机系统运行数据集H,假设它的目标预测变量“总功率”R与其他测量的相关变量x = {x1, x2,…, xi}之间存在f (x1, x2,…, xi) = WHx + b的函数关系,其中,W为权重系数向量,b为偏置项。本文的目的是通过数据分析建模来拟合多联机系统的“总功率”与其他相关变量之间存在函数关系。即多联机系统的能耗预测问题转化为对回归函数f (x1, x2,…, xi) = WHx + b的拟合问题。如果要得到较高精度多联机系统能耗的预测结果,就必须提高回归函数的拟合精度。应用SVM进行回归分析时,需要引进核函数将输入空间通过非线性映射的方式转化到高维的特征空间中并对其进行线性处理,根据核内积并以不敏感损失函数ε为准则,得出非线性的拟合模型并使得其间隔最大。从而使回归函数f (x1, x2,…, xi)的精度达到最大,得到最优的多联机系统能耗预测结果。
1.2 最小二乘支持向量机(LS-SVM)
最小二乘支持向量机[17]将SVM中的不等式约束改为了等式约束,将SVM的损失函数转化为自身的误差平方和,有效避免了SVM求解中存在的二次规划问题,提高了求解效率[18-19]。
对于给定的训练样本(xi, yi)(xi为第i个输入变量,xi= [xi1, xi2, …, xin];yi为与之对应的输出量),通过非线性映射函数φ,将非线性问题转化为高维空间的线性问题,其约束条件如下:
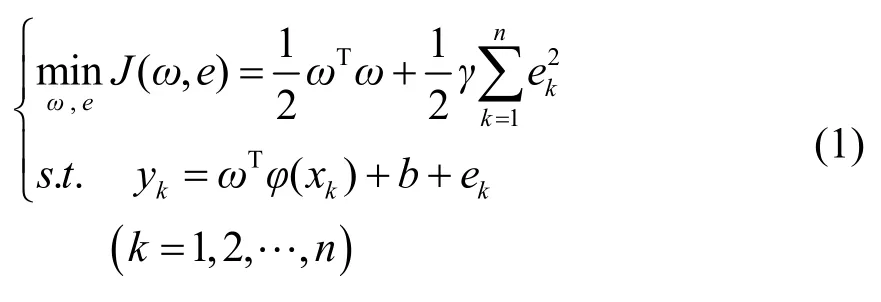
式中:
γ——正则化参数;
ek——误差项;
b——偏置项。
构造拉格朗日函数进行求解:
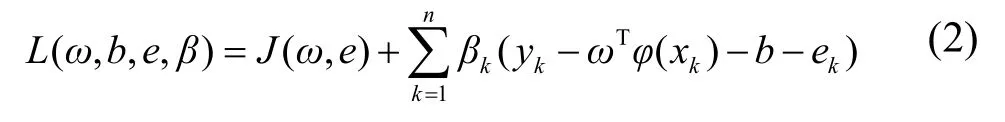
式中:
βi——拉格朗日算子。
根据Karush-Kuhn-Tucker进行优化可得:
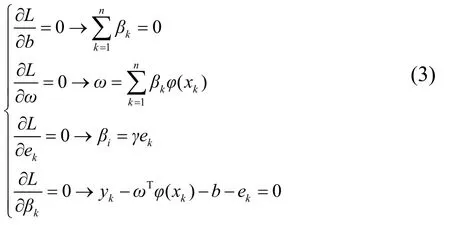
化解式(3)得出矩阵方程:

式(4)中:
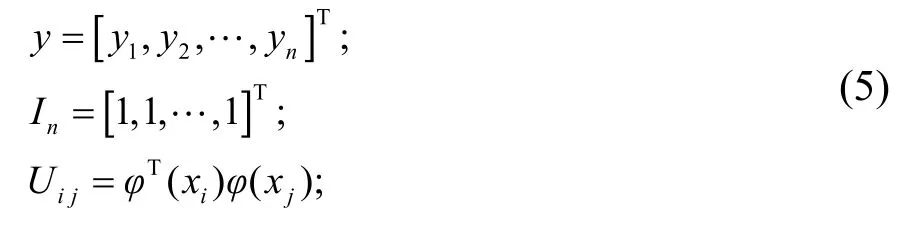
对上式(5)求解得出b和β,则LS-SVM回归模型即为式(6):

1.3 双模型对比诊断体系的构建
箱线图分析虽然能够识别出数据集中存在的异常值,但分析出的异常数据大都属于离群点,而能耗故障数据绝大多数处于群体之中,即箱体内部,分布并没有什么规律,因此,仅运用箱线图分析难以实现故障数据的有效排查。
本文通过选用SVM和LS-SVM两种能耗预测模型,对相同的多联机系统能耗数据进行能耗预测,分别得出两种预测模型出现较大预测误差时所对应的数据,进而对比两种模型中出现较大误差的实验数据集,如果在相同的实验数据上两种模型均发生较大的预测误差,则证明该实验数据存在异常。
2 实验数据来源
图1所示为实验所用的VRF系统结构[20]。根据多联机系统能耗预测问题的需要,在相应机组位置设立传感器来采集可能需要的各类多联机系统运行参数,各传感器位置如图1所示。室外机组额定制冷量为28 kW,室内机组额定制冷量为2.8、3.6、5.0、7.1和11.2 kW。制冷剂为R410A,名义充注量为9.9 kg,压缩机为全封闭涡旋式压缩机。
2.1 实验数据采集
实验前已经对多联机系统和各测量仪器进行了检测,保证各机组部件都能正常有效地运行。实验时设定制冷剂充注量为95.75%进行机组测试,记录的实验数据包含了室内外温度,压缩机运行频率、排气温度、模块温度、壳顶温度、母线电压及电流、模块高压、模块低压、化霜温度、过冷器液出温度、过冷器气出温度、汽分进管温度、汽分出管温度、室外机EXV、过冷器的EXV和总功率共18个参数。
2.2 实验数据预处理
对多联机系统进行数据采样的过程中,由于其采样间隔短、时间长和测点较多等因素影响,数据集中会存在一些缺失值和不变值,从而影响算法的运行效率,需要进行数据的质量分析。为了提升算法的运算效率,需要对采集的数据变量进行相关性分析,筛选变量的个数,优化模型的求解过程。
2.2.1 相关性分析
实验采集的多联机系统运行参数共有18个,除了研究的目标变量“总功率”,剩余的参数数量过多。针对多联机系统的功耗问题,应选取与机组自身的相关变量参数作为研究变量。这些变量中,并非所有的参数都对“总功率”的变化产生影响,或者相对其他参数对“总功率”的影响具有独立性。因此,需要对原始的多联机实验数据集进行数据的特征分析,来确定对“总功率”的变化趋势影响相对较显著的几个变量,并把这些变量的数据和“总功率”作为最终的针对能耗预测模型研究的数据集。将原始多联机运行数据集中所有的测量参数与“总功率”作相关性分析,对筛选出的与多联机机组相关的13个参数分别用字母A到M进行指代,依次为:A-压缩机运行频率、B-压缩机排气温度、C-压缩机壳顶温度、D-化霜温度、E-过冷器液出温度、F-过冷器气出温度、G-汽分进管温度、H-汽分出管温度、I-室外机制热EXV、J-过冷器EXV、K-压缩机电流、L-压缩机模块温度、M-总功率。相关性分析结果如图2所示。
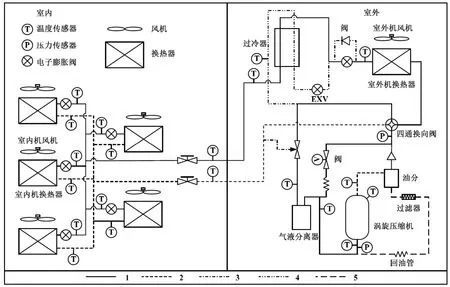
图1 实验所用的VRF系统的结构
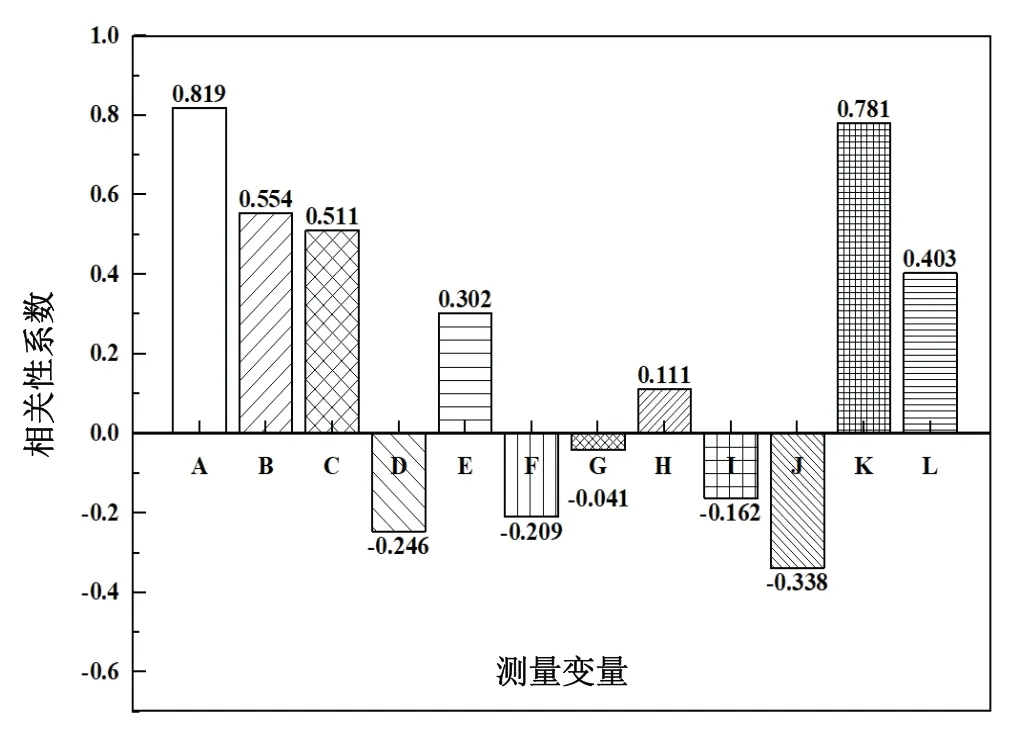
图2 相关性分析图
表1列出了与总功率P相关性较强的几个变量之间的相关性系数大小,依据相关系数的大小,将图2中相关性明显较强的4个运行参数选为预测模型的特征变量。

表1 特征变量相关性系数大小
3 故障数据检测与结果分析
3.1 双模型能耗预测结果
将预处理后的原始数据按80%作为训练集,20%作为测试集的比例进行数据集划分,分别用SVM和LS-SVM两种模型对相同的训练集和测试集进行回归分析,从而得到两组预测结果。将两种预测模型的训练集和测试集的预测结果按相同的排列方式进行整合,对整合后的预测数据集进行对比分析。
将两种预测模型对全部数据(包括训练集和测试集)的预测误差在同一张柱状图上呈现出来,结果如图3所示。图3中,在SVR能耗预测模型预测出现较大误差的数据点上,LS-SVM预测模型也在相同的位置上出现了较大的误差。因此,有理由认为这些能耗预测误差较大的数据点存在数据异常。
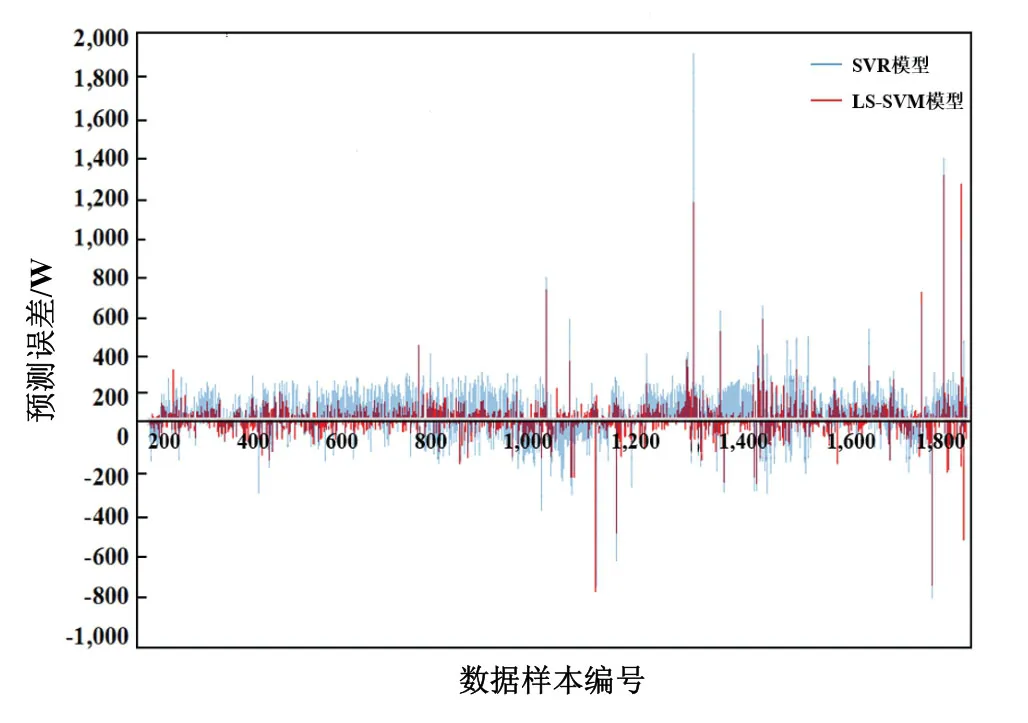
图3 SVM和LS-SVM预测误差柱状图

图4 SVR能耗预测模型预测误差分布
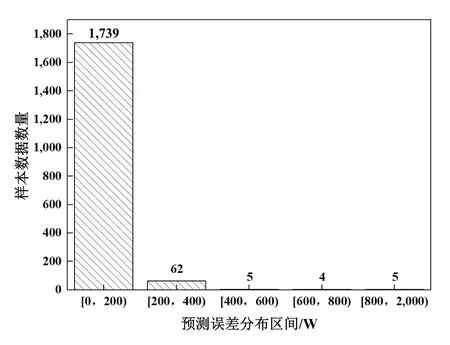
图5 LS-SVM能耗预测模型预测误差分布
图4和图5分别是多联机系统SVR能耗预测模型以及LS-SVM能耗预测模型的预测误差分布,对比两图来看,两者在预测误差大于400 W数据量分布上十分相似。因此,结合图3中的重叠情况,可以判断这些数据存在“能耗数据故障”。
3.2 对比结果分析
根据上述分析,对实验数据进行二次清洗,剔除预测误差过大的少数数据点。对清洗后的实验数据集按之前实验相同的训练集、测试集划分标准,分别再用SVR模型和LS-SVM模型进行回归预测分析,并将测试集和训练集的预测评价结果都与剔除异常值前的预测结果进行比较。
两种能耗预测模型剔除异常值前后各自的训练集和测试集各评价指标分析结果如表2所示。可见不论是训练集还是测试集,两种预测模型在剔除异常数据后的整体预测性能均得到提升,所有的预测性能评价指标的评价结果均得到提升,也再次验证了原始数据中存在能耗数据异常的情况。
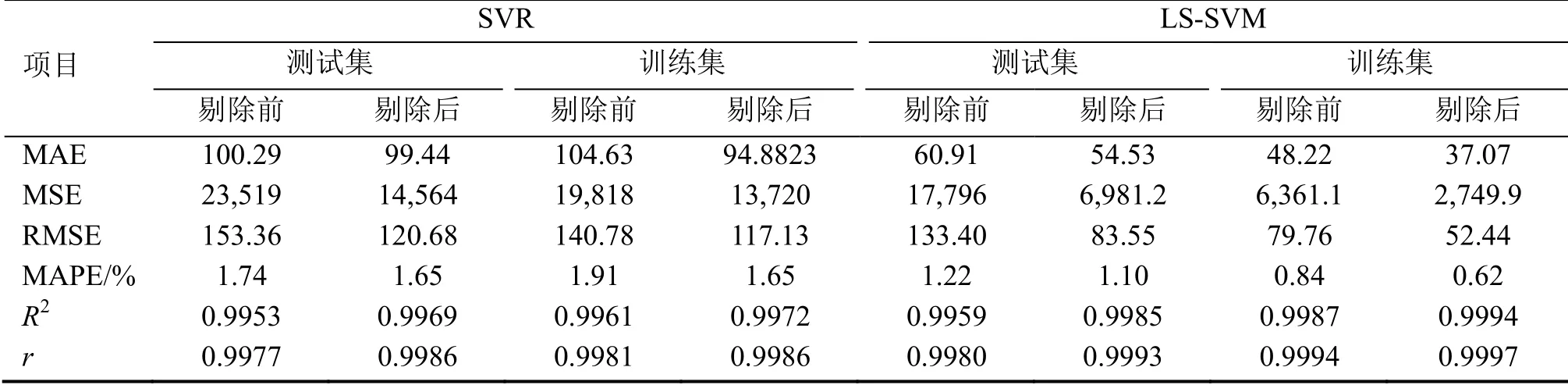
表2 评价指标分析结果
4 结论
本研究运用SVM和LS-SVM对多联机系统的能耗分别进行了预测,并通过预测结果对比分析,判断原始数据集中是否存在“能耗数据故障”的情况,得出如下结论:
1)两种能耗预测模型对相同的多联机系统数据同时产生了较大的预测误差,并且发生这种较大误差的数据分布情况类似,证明多联机系统实验数据集中存在能耗故障数据,应当剔除;
2)剔除筛选出的能耗故障数据后,两种模型的各预测性能评价指标都有很大的优化;特别对于本文的多联机系统SVR能耗预测模型,其稳定性得到很大的提升,预测误差大大减小。

