NCA降维和贝叶斯优化调参对分类模型的改进

李 斌 王卫星

(河南科技大学应用工程学院现代教育技术中心 河南 三门峡 472000)

0 引 言

目前对高校贫困生进行判定的方法大都利用数据挖掘技术定量和定性结合。文献[1]通过能够面向多值属性的关联规则Apriori算法的改进提高了数据挖掘效率，为高校贫困生认定工作提供了有利依据；文献[2-4]对数据预处理并使用C4.5算法，将知识表示成树的形式，采用错误预测率进行修剪，分别归纳出决策树，分析并选出其中较优结果，原理简单且计算快速准确；文献[5]基于加权约束的决策树认定方法提高了贫困生认定效率；文献[6]结合Logistic回归、Native Bayes和k近邻三种分类预测模型综合比较认为k近邻模型能更好地判别出学生是否是贫困生；文献[7]在相同的数据集中证明随机森林算法分类正确率较高。

上述学者针对贫困生判定的研究主要侧重于个别分类算法，对算法的计算成本、性能优化缺乏深入分析，评价方式比较单一化。本文认为高校贫困生识别可以在做好反复训练和评估模型的基础上，集成多个分类算法，运用NCA对特征参数降维以提升计算性能；引入成本惩罚函数并利用贝叶斯超参数调优对分类模型进行进一步优化，以提升分类模型的预测准确率。

1 分类算法的对比选择

分类算法旨在构建分类预测的模型，是人工智能、模式识别和数据挖掘领域中重要的数据处理方法[8]。

1.1 分类算法简述

1.1.1决策树CART

CART(Classification and Regression tree)分类回归树使用基尼指数(Gini)，采用二元切分法选择特征进行训练数据切割：

决策树算法的优点是计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，缺点是易会产生过拟合问题[9-10]。

1.1.2非线性SVM

SVM支持向量机是将低维空间的输入数据投放到一个更高维的特征空间，用线性决策边界分割在低维空间难以区分的正例和负例。在非线性问题上，用内积φ(xi)·φ(xj)代替最优分类面中的点积。

最大化目标函数为：

约束条件：

相应的分类器函数转化为：

SVM的优点是泛化错误率低，计算开销不大，结果易解释;缺点是对主要适用于处理二分类问题，参数调节和核函数的选择敏感，但经过构造可以将多分类问题转化为二分类问题[11]。

1.1.3k-最近邻算法

k-最近邻给每个属性相等的权重进行基于距离的邻近比较。常用的邻近距离是欧几里德距离，两个点或样本X1=(x11,x12,…,x1n)和X2=(x21,x22,…,x2n)的欧几里德距离为：

(6)

k-最近邻分类算法的优点是无数据输入假定、噪声数据影响不大、精度略高;缺点是计算空间复杂度高。

1.1.4贝叶斯方法

贝叶斯是基于贝叶斯定理与特征条件独立假设的分类方法，在数据集D中令A1,A2,…,A|A|为用离散值表示的属性集合，令C为具有|C|个不同值的类别属性，假设所有属性都是条件独立于类别C=cj，数学表示为：

P=(A1=a1|A2=a2,…,A|A|=a|A|,C=cj)=P(A1=ai|C=cj)

从训练数据中可以直接得到先验概率P(C=cj)和条件概率P(A1=ai)，贝叶斯的分类公式为：

贝叶斯法的优点即使数据较少也可高效处理多类别问题;缺点是对于数据输入假设条件较为敏感。

1.1.5BP神经网络

神经网络是由一个输入层、若干个隐含层和一个输出层组成的多层网络，各层之间的连接方式通过权重值调节。若模型确定训练误差的理想输出是tk，实际输出是zk，c代表输出向量的长度，ω代表网络的所有权值，η是学习速率，那么总误差表示为：

(8)

基于梯度下降的误差反向传播算法BP神经网络是沿着减小误差的方向来调整权值：

BP算法对网络拓扑及初始权重敏感，泛化性能往往不能得到保证，容易陷入局部最小[12-14]。

综上所述，将几种典型的机器分类算法的对比总结如表1所示。

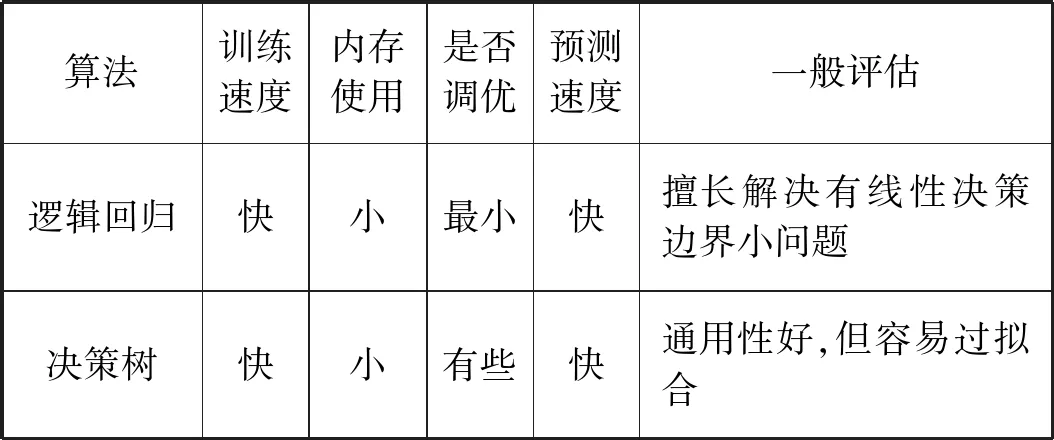
表1 几种分类算法分析比较

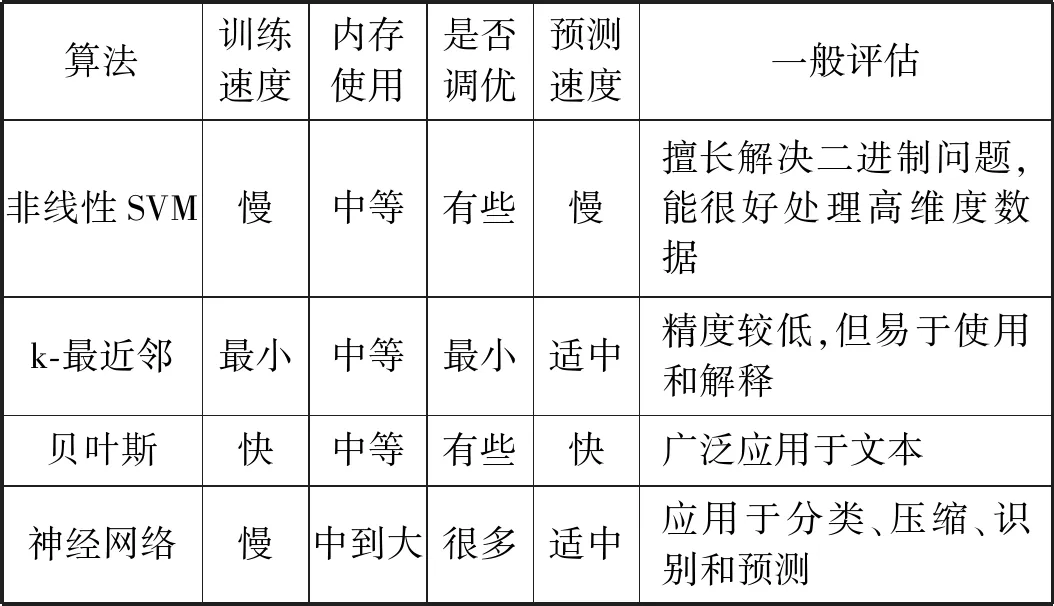
续表1

1.2 分类算法的选择

在机器学习领域里，一方面高度灵活的模型由于拟合了噪声数据的细微变化易造成过拟合，另一方面简单的模型可能又需有更多的假设条件。在模型速度、准确性和复杂性之间的权衡本已不易，算法的选择还取决于要处理的数据的大小和类型以及如何运用从数据中获得的洞察力，因此不存在一种万能的算法可以完美解决所有问题。

在对高校贫困生预测判定建模时，需要做好反复训练和评估模型的准备。既可运行所有算法进行比较，也可从特定分类任务的经验最佳拟合算法开始。对每个训练的分类器，要保留验证数据或反复使用交叉验证对精确度进行评估，最终尝试集成多类分类算法克服训练数据的过拟合。

2 算法模型的改进优化

分类模型的改进优化意味着进一步提高其准确性和预测能力，避免模型无法区分数据和噪声时过拟合。本文在对分类模型经反复评估初步确定后，对模型的改进优化手段主要采取邻域向量分析NCA特征降维和贝叶斯超参数调优。

2.1 NCA特征降维

特征降维是向模型添加变量或移除不能改进模型性能的变量，以在数据建模中提供最佳预测能力[15]。特征降维不但可以降低计算成本和存储要求，还能使预测结果更加精确。

NCA是一种距离测度学习算法。该算法随机选择近邻，通过优化留一法(Leave-one-out, LOO)的交叉检验结果来求得马氏距离中的变换矩阵。在这个过程中完成降维，最后在低维空间对数据完成分类。

数据集X={x1，x2，…，xn}在RD空间内分别具有类标签c1，c2，…，cn，限定马氏距离变换矩阵Q=ATA，两个样本点之间的马氏距离定义为：

i，j=1，2，…，n

(10)

样本点xi随机选择一个xj近邻并继承其类标签cj的概率Pij，概率Pij在变化空间中使用欧式距离定义如下：

因为每个数据点都可以选择为近邻，因此输入数据可以继承所有的类标签，样本点xi正确分类的概率为：

(12)

NCA搜索变换矩阵A，目标函数可以理解为要使得正确分类的点数最大化期望，也就等同于最小化类间距离：

(13)

这个无约束优化问题通过共轭梯度法或随机梯度法求出A，使用微分的变换矩阵：

式中：xij=xi-xj,当A是d×D的非方阵时，经过NCA距离测度学习可以将样本降到RD空间[16-17]。

实际应用中，由于共轭梯度法通过多次迭代才能得到目标函数最优解，占用内存的同时耗时较大，因此使用等价于共轭梯度的拟牛顿法基础上的L-BFGS(Limited-memory BFGS)算法进行计算，其中BFGS是四个提出这种拟牛顿法的四个人名的首字母。L-BFGS算法的核心是不再存储完整的矩阵，而是存储计算过程中的向量序列，且只利用最新的向量序列，以大幅降低运算成本。

2.2 超参数调优

识别能提供最佳模型的参数集的过程可称为超参数调优。两个常用的参数调优方法是网格搜索和贝叶斯优化。虽然网格搜索能彻底搜索参数值组合的有限集，但耗时太长并易遇到维度灾难。

贝叶斯参数优化充分利用被测试点忽略的前一个点的信息[18]。它根据先验分布假设一个搜集函数，使用每次新采样点去测试目标函数的信息来更新目标函数的先验分布。然后测试由后验分布给出的全局最值最可能出现的位置点。贝叶斯优化虽需执行更多的迭代计算以确定下一个采样点，但可以较少的评估就找到复杂非凸函数的最小值，主要分三个步骤：

(1) 选择一个先验函数来表达关于被优化函数的假设。本文选择使用的高斯过程是一个随机变量的集合，任意有限个随机变量都满足一个联合高斯分布[9]。若X表示训练集{x1,x2,…,xt}，f表示未知函数值集合{f(x1),f(x2),…,f(xt)}，Σ表示k(x,x′)构成的协方差矩阵Ⅱ，θ表示超参数，当存在观测噪声且假设噪声ε满足独立同分布的高斯分布p(ε)=N(0,σ2)，可以得到边际似然分布为：

(15)

式中：y表示观测值集合{y1,y2,…,yt}。

然后选择采集函数用来从后验模型构造一个效用函数，来确定下一个采样点[20-22]。采集函数可以在具有低建模目标函数的点上对采样进行平衡，并对尚未建模区域进行搜索。

贝叶斯超参数调优的算法步骤如算法1所示。

算法1贝叶斯优化算法

Bayesian optimization：选取n个采样点作为先验，假设它们服从高斯分布

1： forn=1，2，…,n，do

2： 根据最大化采集函数α选取下一个采集点xn+1

3： 查询目标函数以获得yn+1

4： 整合数据集Dn+1={Dn,(xn+1,yn+1)}

5： 更新概率模型

6： end for

为提高找到最优参数值的机率，并使超参数调优更加高效，使用MATLAB中的贝叶斯优化工具执行超参数调优，同时引入成本函数对错误分类进行惩罚。

3 应用实证

高校贫困学生的贫困成因多集中在家庭经济情况、生活水平、家庭劳动力状况、在校消费能力水平、消费习惯、学业水平、学习主动力等方面[23]。

本文通过某高校2016-2017年度校园应用服务中积累的数据。首先选择训练数据进行分类学习，反复训练和评估分类模型后选择合适的分类算法。然后采用NCA特征降维和贝叶斯参数调优对模型进行优化，对某高校的贫困生的精准判定实现预测和评判。

3.1 选择训练数据和算法验证

样本数据会以各种形式和大小出现，如高校贫困生的真实数据集可能较混乱、不完整且采用格式各异。对高校各个业务子系统中得到的原始数据进行预处理需采用专业数据处理工具和不同的预处理方法。

将从高校各个应用系统中抽取出的数据进行标签标记、清理无效数据、分类汇总后得到完整的样本数据共9 909组。这些组样本数据初步特征值共有21种，其中部分特征来源于学生调查问卷等，并对部分数据进行了离散化处理，如表2所示。

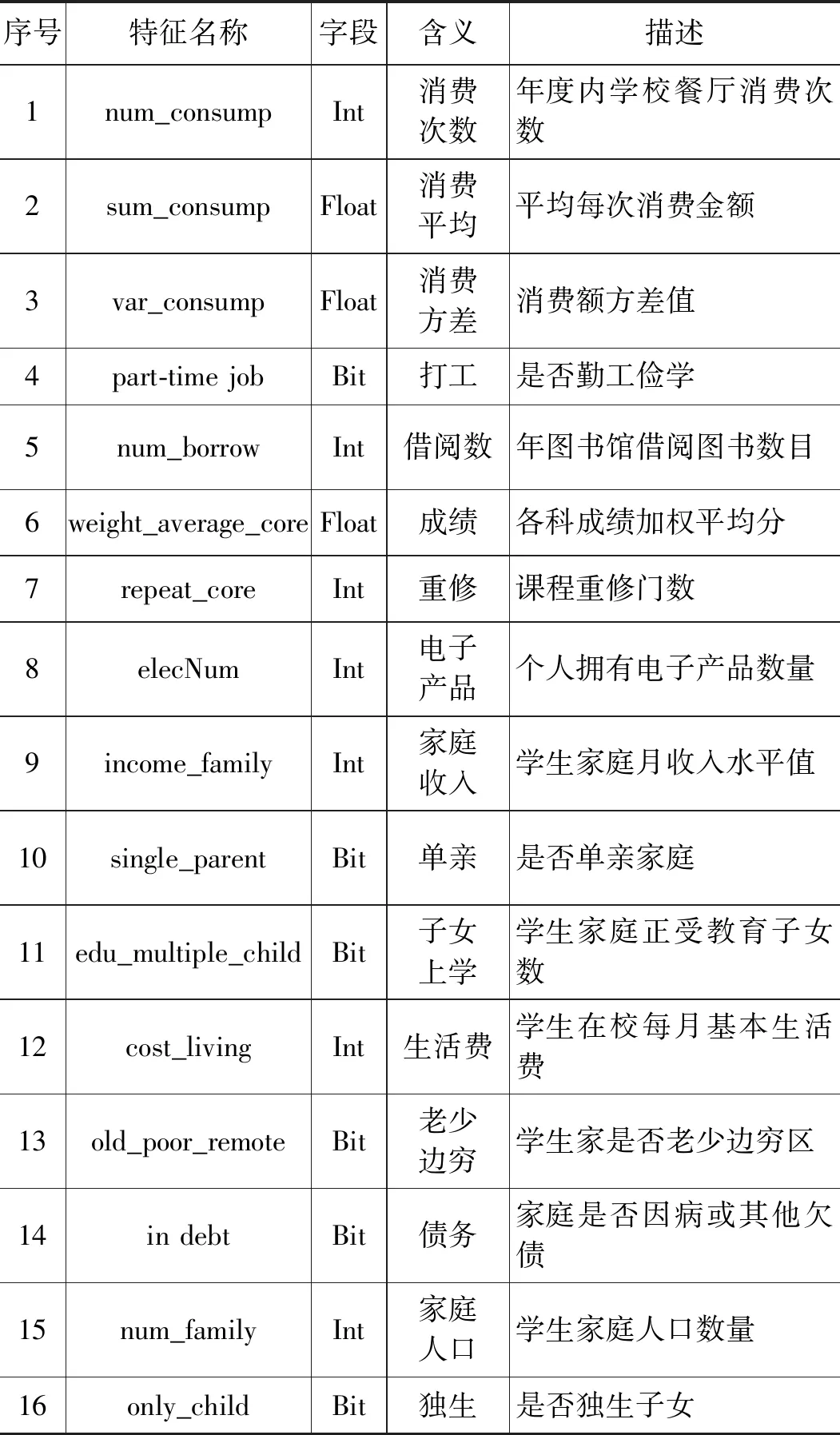
表2 样本特征值列表

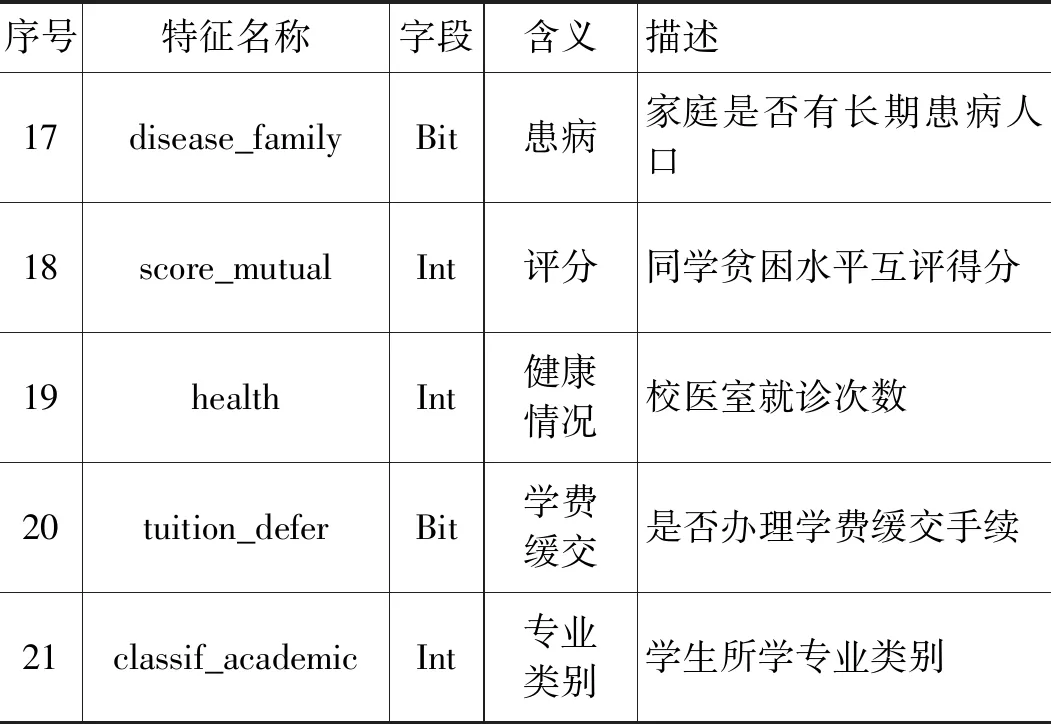
续表2

在MATLAB中将经过初步清噪脱敏后的数据导入，对数据样本采用k折交叉验证，k值取5，每次以k-1份作为训练集，1份作为验证集。得到验证集性能后，将5次结果平均作为模型的性能指标，以最大化使用模型训练的数据量，得到泛化更好的模型。MATLAB中多个分类器的性能比较和分类初始结果如图1所示。

图1 多个分类算法的初始比较图

从图1中可以看出，训练样本明显地被分为common、poorer和poorest三类灰度程度不同的颜色，其中的“×”为噪声数据。实证对比算法模型结果，高校贫困生预测最初显示二次支持向量机(SVM)表现良好，然后是线性支持向量机和决策树算法。不同分类器的时间消耗和准确率性能比较如表3所示。

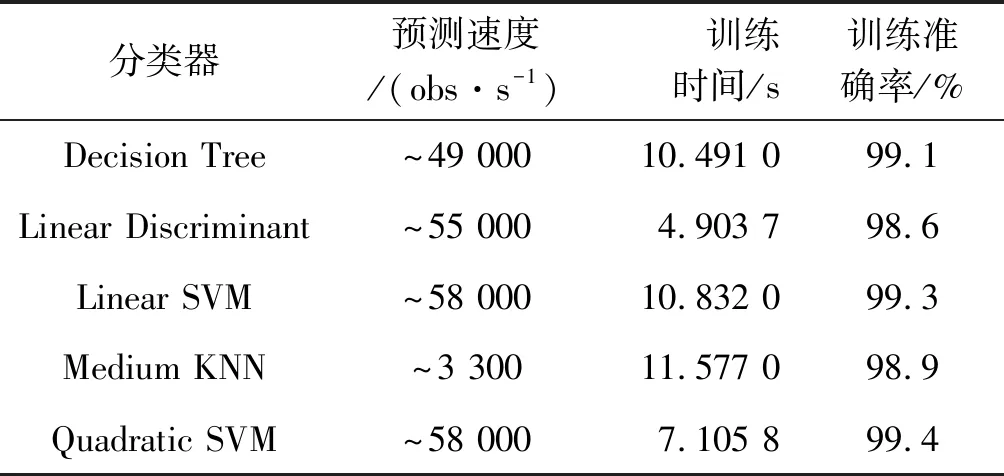
表3 不同分类算法的初始性能比较

3.2 运用NCA进行特征降维

在处理高校贫困生涉及的数据集包含大量特征和有限的观察值时，运用NCA特征选择技术降维，具体步骤如下：

Step1将训练数据分成5份，使用CVpartition进行交叉验证，赋值λ并创建一个数组阵列来存储损失函数值。

Step2使用每部分中的训练集，为每个值训练NCA模型。使用NCA模型计算每部分中相应测试集的分类损失，记录损失值。

Step3重复所有部分训练值和λ值，计算得出每个λ值的每个部分的平均损失。绘制平均损失值与λ值之间的关系，找到与最小平均损失对应的最佳λ值。

Step4使用最佳λ值拟合NCA模型，使用计算效率更好的L-BFGS算法去求解目标函数，标准化预测值绘制特征权重。

图2显示了在MATLAB中使用邻域分量分析NCA识别的特征权重结果，圆圈表示对应特征的特征权重。可以看出特征指标1(num_consump)、2(sum_consump)、3(var_consump)、9(income_family)、18(score_mutual)、12(cost_living)、6(weight_average_core)、8(elecNum)、14(indebt)、17(disease_family)、19(tuition_defer)的特征权重值高于相对阈值0.374 6。利用MATLAB中自带的NCA降维揭示了在贫困生特征中大约一半的特征对模型没有重要作用。因此，我们可以减少特征数量，从21个减至11个。

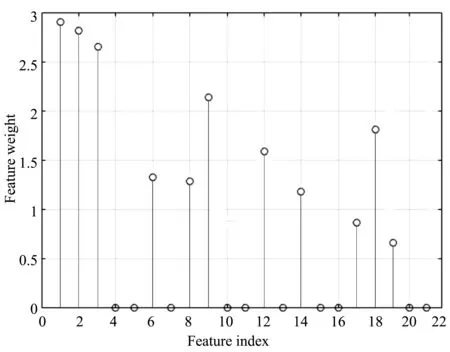
图2 使用邻域分量分析NCA识别最相关的特征结果

按照NCA降维后的特征选择，重复前述分类算法，比较不同算法降维后的各项性能参数如表4所示。

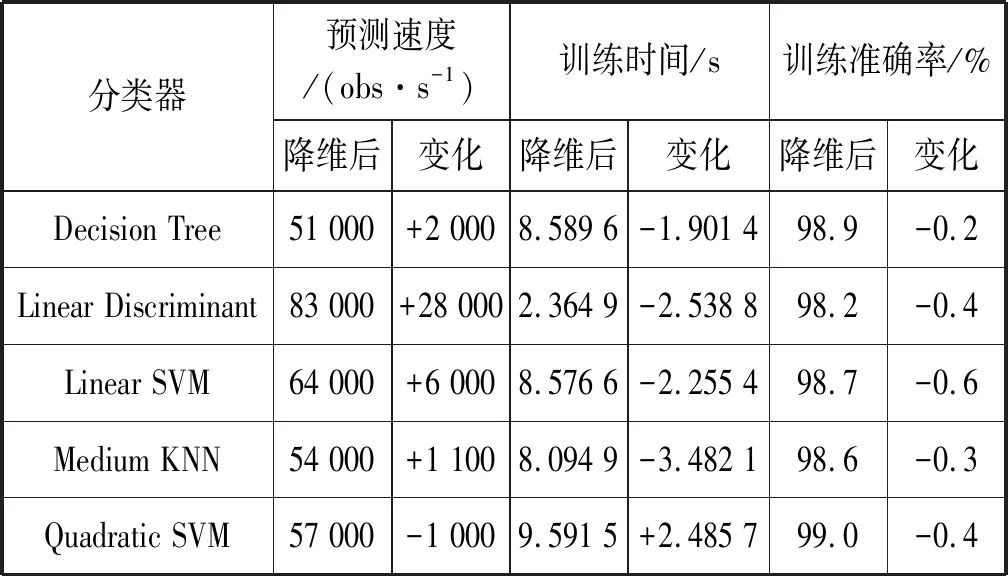
表4 不同分类算法NCA降维后性能比较

从表4的几种分类算法的性能变化值可以明显看出，NCA降维后，整体预测速度和计算时间变化明显，特别是线性判别算法因为特征数的大幅减少而性能大幅提升，决策树分类算法表现优异。

使用单独的分类算法往往会过度拟合训练数据，为了克服这种倾向，可以尝试集成多个分类算法，典型的比如Boosted Trees和Bagged Trees。测试表明这两种集成分类算法在降维后的准确率仍可以达到99.3%。从上述算法对比中也可以看出，某些算法初始表现很好，改进后表现一般，有的反之。所以可以后退到特征提取阶段去寻找其他特征并降维，在机器学习工作流程的不同阶段之间反复实验和对比，寻找最佳模型。

3.3 引入成本函数的超参数调优

在高校贫困生预测分类模型中，单单根据总体精确度分析性能很容易产生误导，比如未能准确预测实际贫困相比错误地将正常情况学生误判为贫困要造成更大的不公平。图3所示的初步模型分类结果混淆矩阵，将3%的贫困生误报为正常学生，而将8%的普通学生分类为贫困和极度贫困。这将造成部分学生的评判结果失真，不需补助的学生得到补助，而急需补助的学生却失去应有的补助。

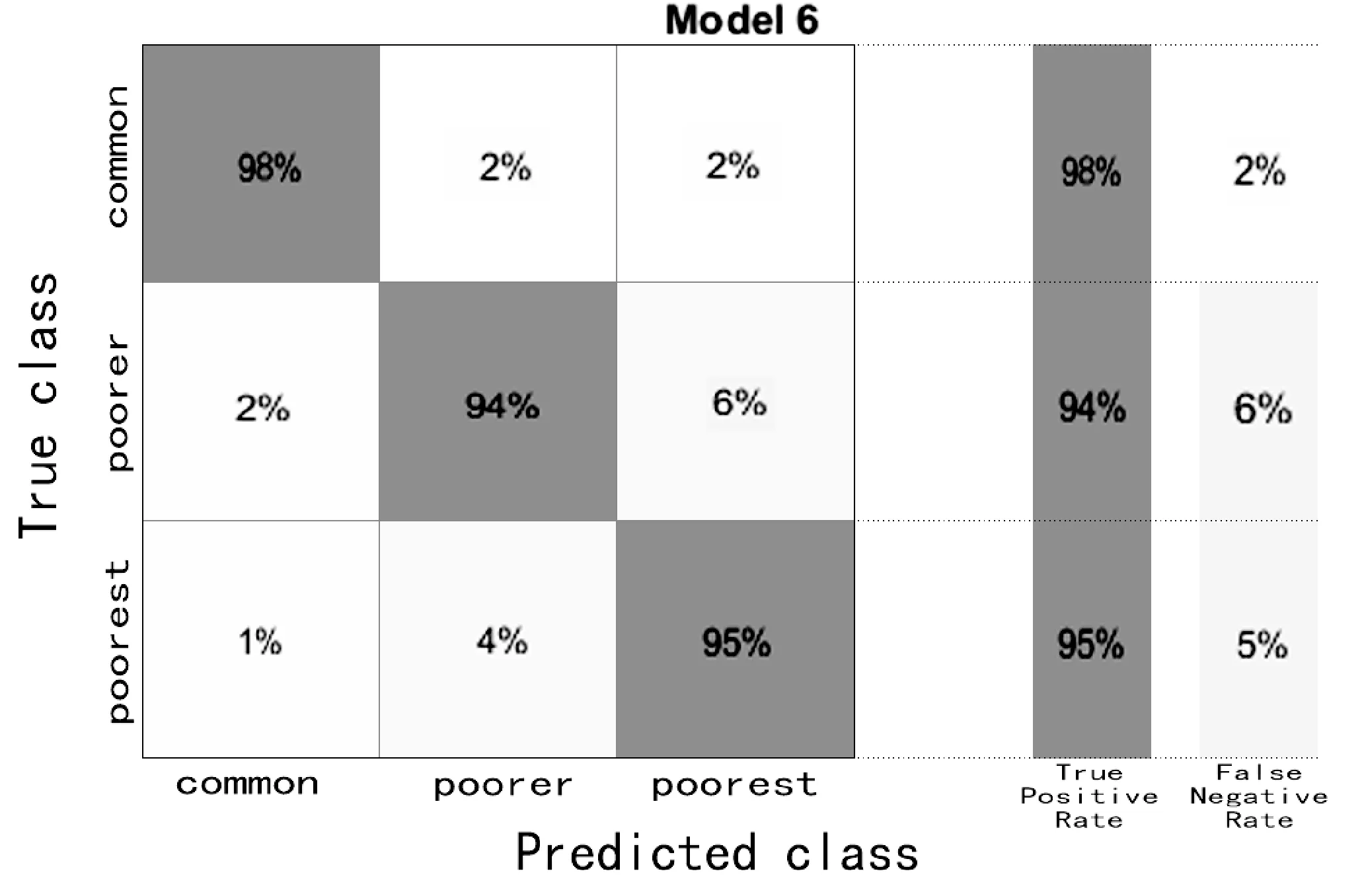
图3 初步模型的混淆矩阵

为了改进分类器，引入成本函数对误分类进行惩罚，补偿数据中较少的“异常”观察，并使分类器偏向于较少的错误分类异常噪声，将较高的错误分类成本分配给“异常”类。同时利用贝叶斯优化方法对模型参数进行超参数调优。由于Trees的表现优于SVM，本文以生成树为效果目标，步骤如下：

Step1因为是common、poorer和poorest多分类，首先使用AdaBoostM1和Trees模型5倍交叉验证分类，指定每个Trees最多被分割5次。然后对“common”的误分类分配一个高成本值20以进行惩罚，即引入置信度的AdaBoostM2模型进行对比。

Step2在MATLAB中选用Bayseopt工具箱[24]，使用fitcensemble找到使交叉验证损失最小化5倍的超参数，设置随机种子值并使用“expected-improvement-plus”采集函数确定下一个要评估的点，并在置信区域内进行探索。为了重复并可视化，将它们传递到OptimizeHyperparameters名称-值对中，需要优化的参数默认为KernelScale和BoxConstraint。

Step3传递参数作为优化超参数的值后命令行中会出现迭代显示，超参数调优结果如图4所示，目标函数为回归的log(1+交叉验证损失)和分类的误分类率。进行迭代以优化超参数、最小化分类器的交叉验证损失，使用经过优化超参数训练的模型预测验证集的类标签，可以看出经过迭代后泛化能力拟合。图4中的稍小圆点表明目标点，稍大圆点标明采集函数值最大的位置并以此作为下一个采集点。最佳估计可行点是根据最新模型估计均值最低的采集点，最佳观测可行点是目标函数评价返回值最低的采集点。

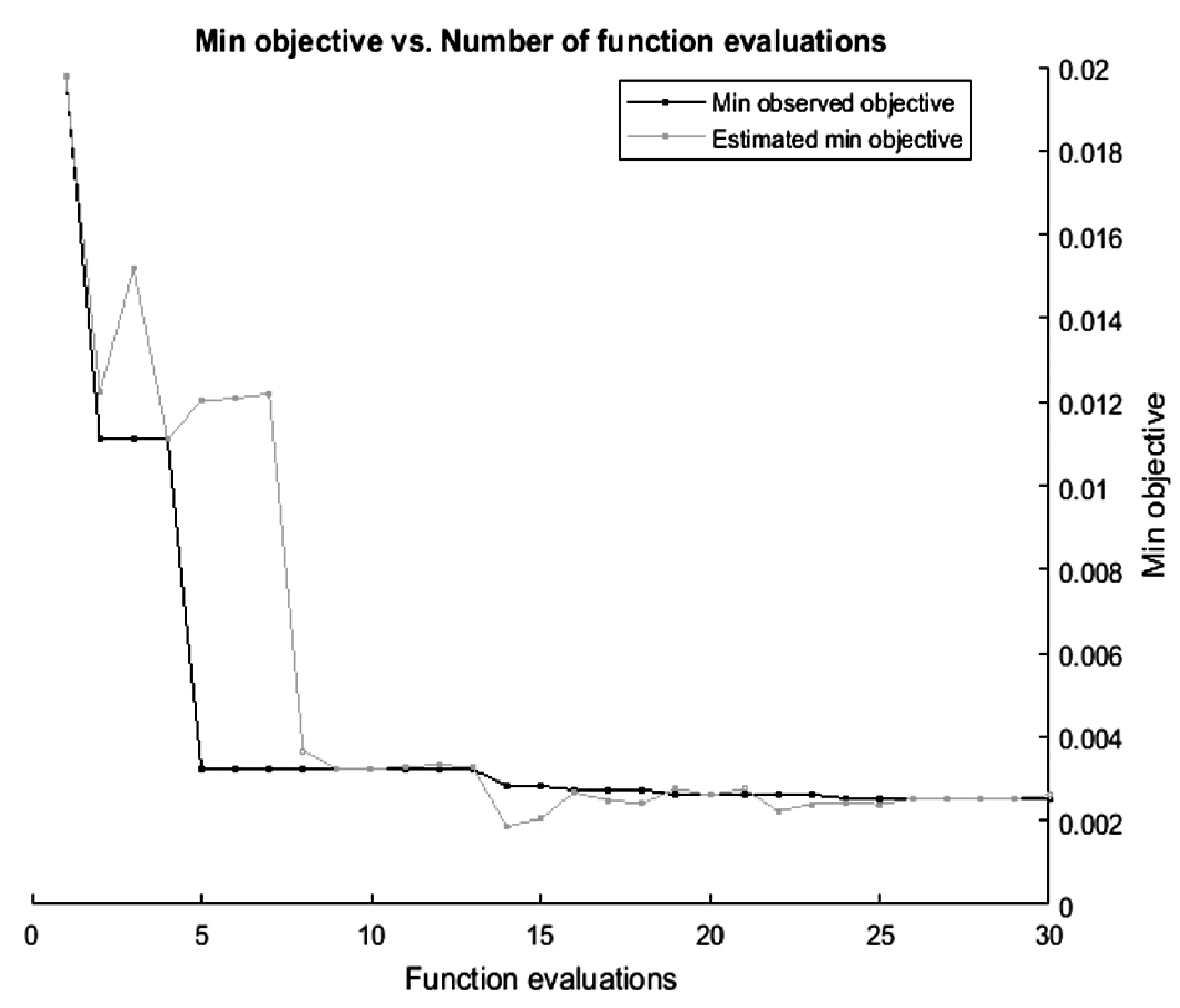
图4 超参数调优迭代过程和结果

表5说明了采用集成分类AdaBoostM2经过贝叶斯超参数调优后最佳估计可行点和最佳观测可行点的比较结果。可以看出准确率由93.45%提升到了97.49%，函数计算时间成本约降低了14 s，优化效果明显。

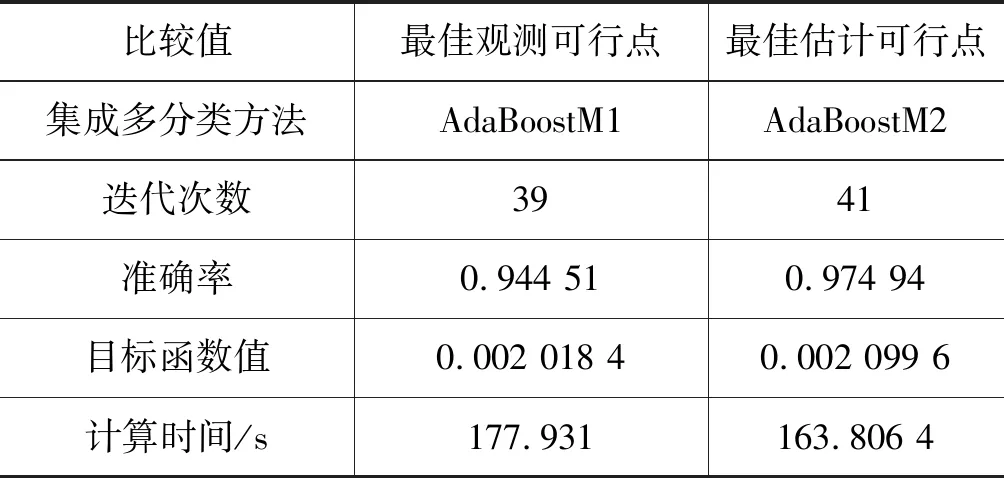
表5 超参数调优后最佳估计可行点和最佳观测可行点比较

Step4利用MATLAB中的混淆矩阵生成函数Confusion Matrix和热图生成函数Heatmap将经过训练的模型预测验证集的类标签，生成优化后的多分类混淆矩阵并可视化，如图5所示。

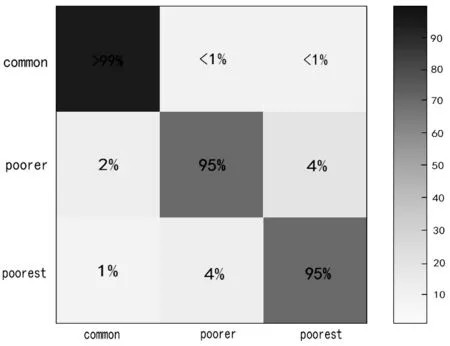
图5 模型优化后的多分类标签混淆矩阵

从优化后的多分类标签混淆矩阵可以看出，经过NCA降维后引入成本函数惩罚并用贝叶斯超参数优化后的模型将初步模型8%的普通学生分类为贫困和极度贫困误报率减少到5%，模型的准确率明显提升，达到了优化效果。

4 结 语

高校贫困生预测判定建模运行了多种算法训练分类器，单独的分类算法会过度拟合训练数据，而且没有一种算法是万能最优，反复训练试错才是选择最佳算法的前提。对比算法模型结果，二次支持向量机(SVM)、线性支持向量机和决策树算法表现略优。使用NCA方法降维后，整体预测速度和计算时间变化明显，决策树分类算法表现优异。集成分类算法Boosted Trees和Bagged是提升泛化能力的合理有效选择。

在初始模型上保留验证数据，使用AdaBoostM1和Trees模型k折交叉验证反复评估，与引入成本函数权重值调整的AdaBoostM2模型经贝叶斯超参数调优后对比。高校贫困生预测判定AdaBoostM2模型的准确率提升了近4%，计算时间成本降低了14 s，误判率由初始的8%改进到5%，说明优化改进后的算法模型的泛化能力得到了一定的改进。