基于多密度峰值的CFSFDP算法改进
孙 绵 侯再恩 韩肖赟
(陕西科技大学文理学院 西安 710021)
0 引 言
基于密度的聚类算法是遵循数据点的密集程度展开聚类,主要针对任意形状的数据集。经典的基于密度的聚类算法有OPTICS算法、DBSCAN算法等,其中,OPTICS算法存在扩展性低、算法复杂度高的缺陷;DBSCAN算法对输入参数敏感、聚类收敛时间较长等。
针对这些不足,CFSFDP算法[1]作为一种新的密度算法被提出,其对任意形状的数据集尤其是非球形数据集能够有效识别,并且算法仅需设定一个参数,算法结果对参数选取也不敏感[2]。同时因为其算法原理简单易实现、聚类效果优而备受关注。经过深入研究,尽管该算法有许多优点,但是也存在一些缺陷有待完善。文献[3-4]采用簇中心点自动选择策略,避免通过决策图主观确定聚类中心个数带来的误差;文献[5]将模糊的概念用到CFSFDP算法来实现聚类中心的自适应选取;文献[6]利用局部反差方法解决了CFSFDP算法难以发现稀疏类簇的问题;文献[7-8]采用熵实现了截断距离的自适应,并取得了良好的聚类效果;文献[9-12]提出了一种基于网格的CFSFDP算法,该算法利用网格划分来计算局部密度并降低算法的时间复杂度;文献[13]将密度比例引入到CFSFDP算法,解决了对类簇间密度较小数据集不能很好聚类的问题,提高了聚类准确率;文献[14]为了克服无法准确聚类多密度峰值的缺陷,提出了一种基于近邻距离曲线和类合并优化的CFSFDP算法。
考虑到单个簇中存在多密度峰值时易造成簇的分裂,以及利用决策图无法正确选取存在多个聚类中心个数的问题,本文提出把所有密度大于当前位置的数据点以及与当前位置的最小距离分别做成一个集合,对局部密度进行排序。在存在多个密度峰值时,仅选择第一个点作为聚类中心,并且利用归一化的γ函数数值分布做决策图辅助图选取聚类中心数量。模拟实验结果表明,本文提出的改进CFSFDP算法与CFSFDP相比,聚类效果更好,更适合于对较低维度的不规则形数据集进行聚类。
1 CFSFDP算法
CFSFDP算法是一种简洁优美的聚类算法,可识别任意形状的类簇,并且仅有一个参数。核心思想是,在聚类中心的选择中,聚类中心本身具有相对高的密度,而密度较大的其他数据点之间的距离相对较大。
算法的基本模型是:
1) 计算各数据点的密度以及高局部密度点距离;
2) 根据γ函数选取聚类中心;
3) 对非聚类中心点进行聚类,确定每个数据点的最终归类。
1) 局部密度ρ。计算局部密度有截断核和高斯核两种方式,前者定义如下:
(1)
式中:
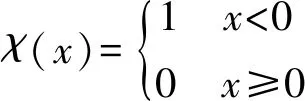
高斯核定义为:
(2)
式中:IS={1,2,…,N}为数据集S对应的指标集,dij=dist(xi,xj)表示数据点xi和xj之间的距离,参数dc>0,需提前设定,通常取所有数据点两两之间的距离经过升序排列后的前1%~2%。
截断核表示离散值,高斯核表示连续值。考虑到截断核对于不同数据点易出现具有同一局部密度值的情况,本文采用高斯核计算方式。
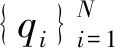
ρq1≥ρq2≥…≥ρqN
则考虑δi定义如下:
由定义可知当数据点xqi具有最大局部密度时,δqj取最大值,足以保证xqi被选为聚类中心。
3) 决策图。文献[2]中对28个数据点的原始数据图分布以及关于(ρ,δ)做出的决策图如图1所示,决策图对聚类中心的选取起着关键作用。对照图1(a)和(b)发现,1号和10号数据点同时有着较大的ρ和δ值,并且恰好是原始数据集中的聚类中心;而对于26、27、28号数据,由于其δ值很大,ρ值很小,在原始数据集中充当离群点。上述聚类中心的选取方案中定性因素太多,即使是同样的决策图,不同的人得到的结果也不同,尤其是对有着多个聚类中心并且个数难以确定的数据,利用决策图无法正确选出聚类中心。文献[2]中提到综合考虑ρ和δ值,建立γ函数,依据γi=ρiδi的值选取聚类中心,值越大,越有可能是聚类中心。并将所有γ值进行降序排列,取前若干个数据点作为聚类中心即可,但是若干个并非自动选取,也是带有一定的主观性。同时,对于较大的γ值存在ρ值很大δ值很小或者δ值很大ρ值很小的情况,易误将离群点选作聚类中心。针对这一缺陷,本文将做出一定改进,提高聚类中心选取的准确率。
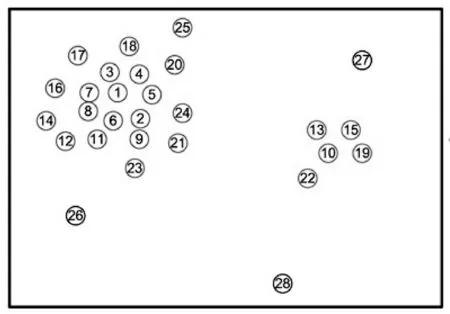
(a)
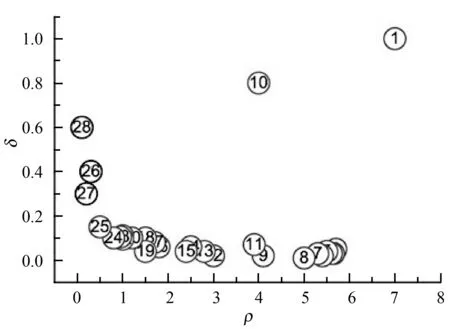
(b)图1 关于决策图的实例示意图
2 CFSFDP算法的改进
2.1 距离δ的确定
对于单个簇中存在多个密度大于自身且距离自身的最小距离δ相同的数据点,这些点均易被选为聚类中心,从而造成簇的分裂,以及聚类中心的多选。
针对这一问题,对式(2)所得数据点的密度进行降序排列,形成先后顺序,并且对点密度大于当前点的所有数据点以及与当前点的所有最小距离分别做成一个集合,保证在存在多个密度大于自己且距离自己最近的点中只选择排在前面的第一个点作为聚类中心,避免簇的分裂。
2.2 聚类中心的选取
针对CFSFDP算法易将数据集中密度大而距离小或者距离大而密度小的数据点选为聚类中心,从而造成聚类中心的错选,文献[8]提出利用信息熵实现截断距离dc的自适应,并将得到的最优值设为潜在聚类中心的距离阈值,避免将密度大而距离小的数据错选为聚类中心。
本文分析了局部密度和最小距离的数值,可知它们是两个不同数量级的。为了避免不同数量级数字之间相互影响,防止大数吃小数等情况,对其进行归一 化处理,原始数据经过处理后,各指标处于同一数量级的,使得聚类中心点到非聚类中心点的γ值变化趋势更加明显,尤其是非聚类中心点的γ值变化趋势更加平滑,从而实现聚类中心的正确选取。
文献[2]中提到聚类中心的选取依靠γ函数,综合考虑ρ和δ值,定义如下:
γi=ρiδii∈IS
本文选用max-min标准化方法,对ρ和δ原始数据进行线性变换,则γ函数重新定义如下:
对有着多个聚类中心并且个数难以确定的数据集,利用决策图无法正确选取出聚类中心。利用上式求出各数据点的γ值,并对各数据点γ值的分布做决策图辅助图,图中从聚类中心到非聚类中心时会有一个明显的跳跃,根据这个趋势可实现聚类中心个数的准确选取。
综上所述,改进CFSFDP算法以代价函数取得最小值作为聚类准则:
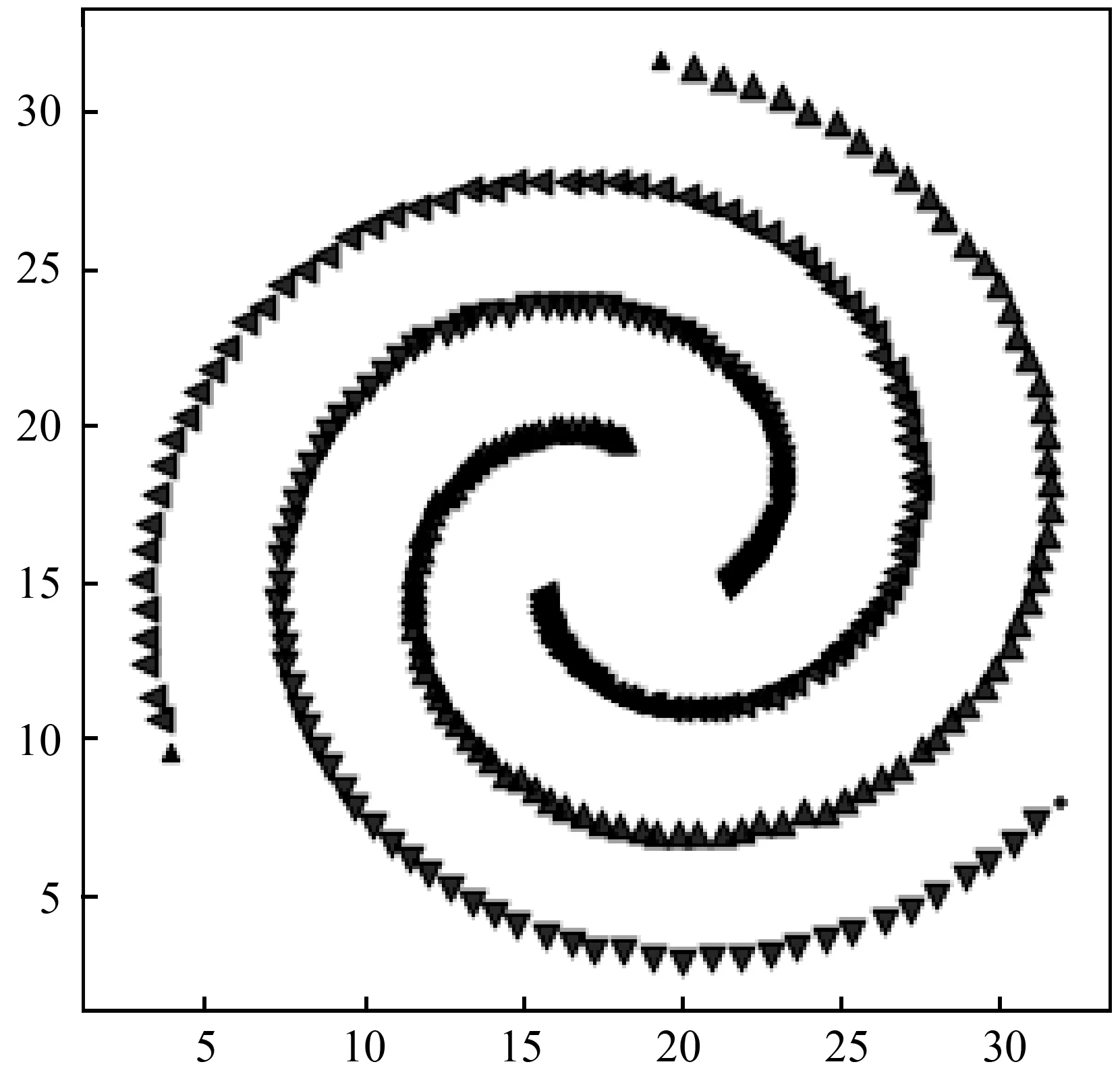
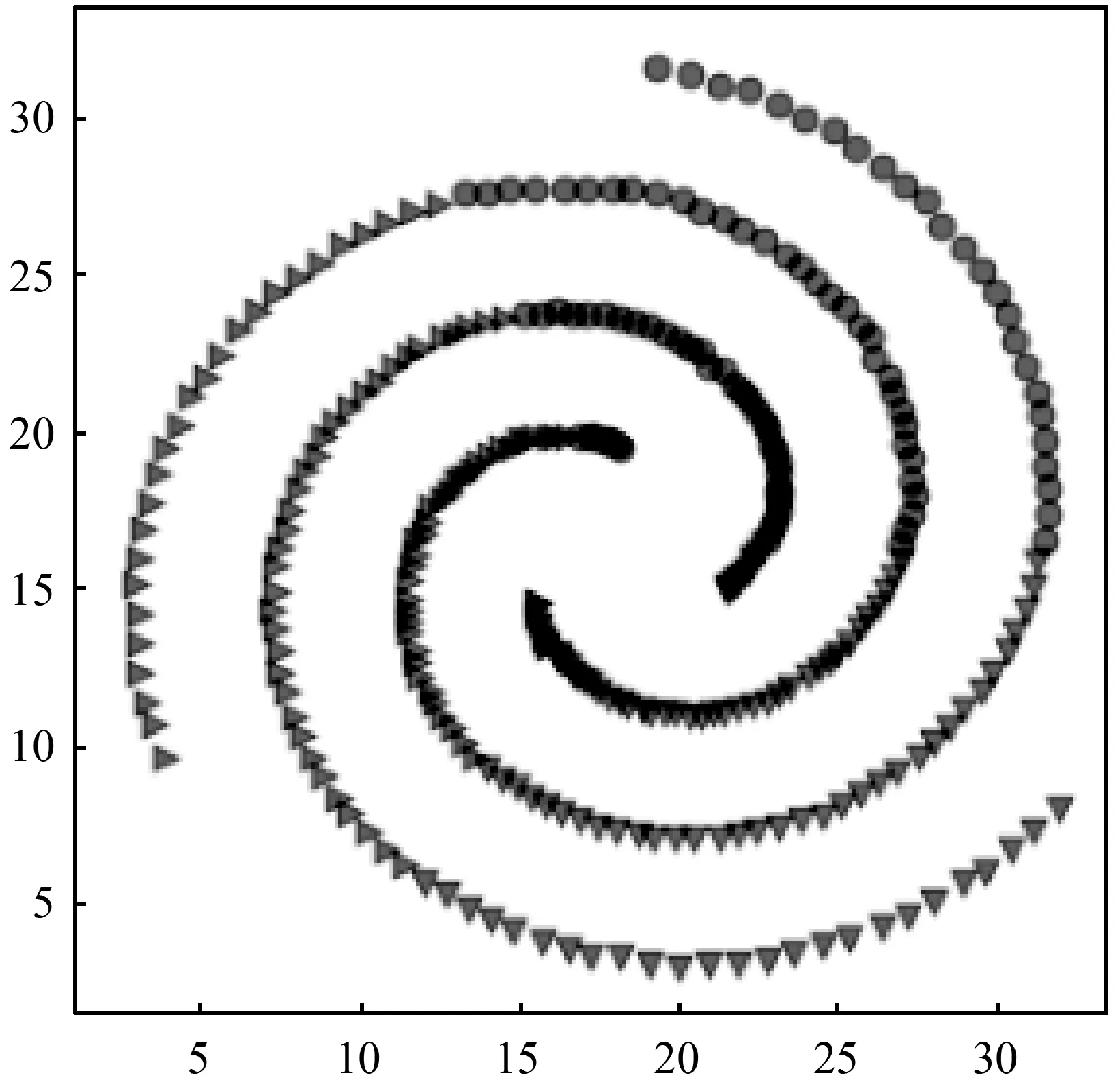
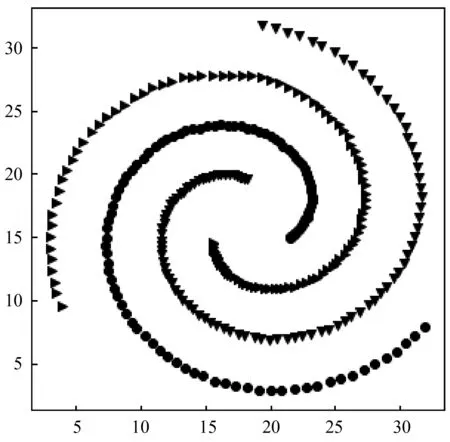
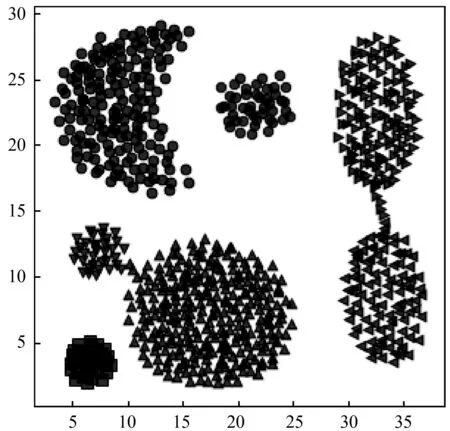
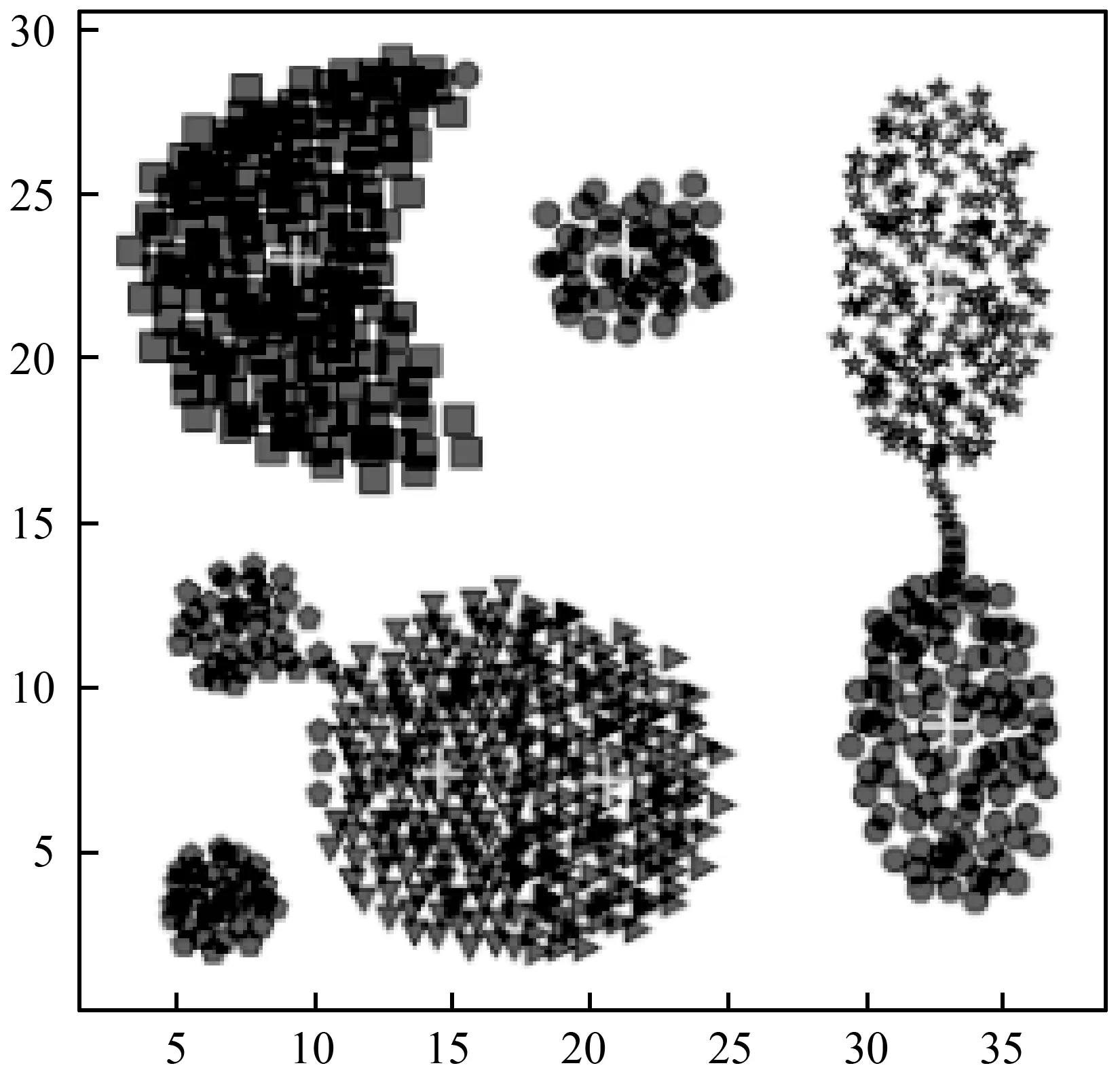
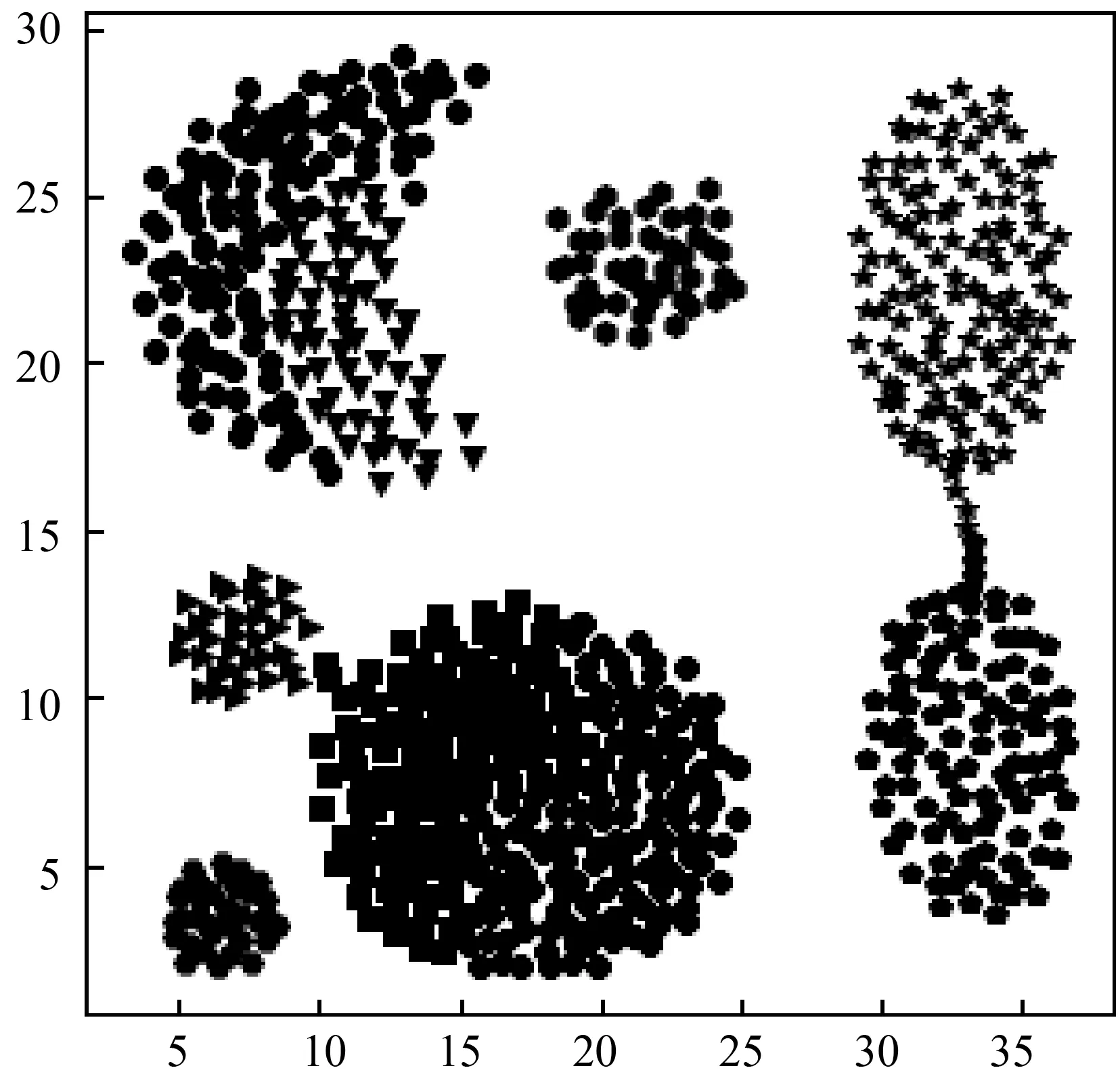
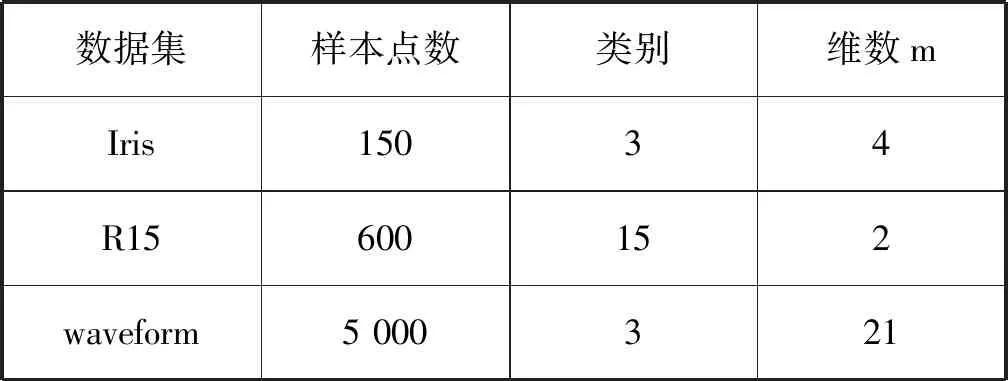
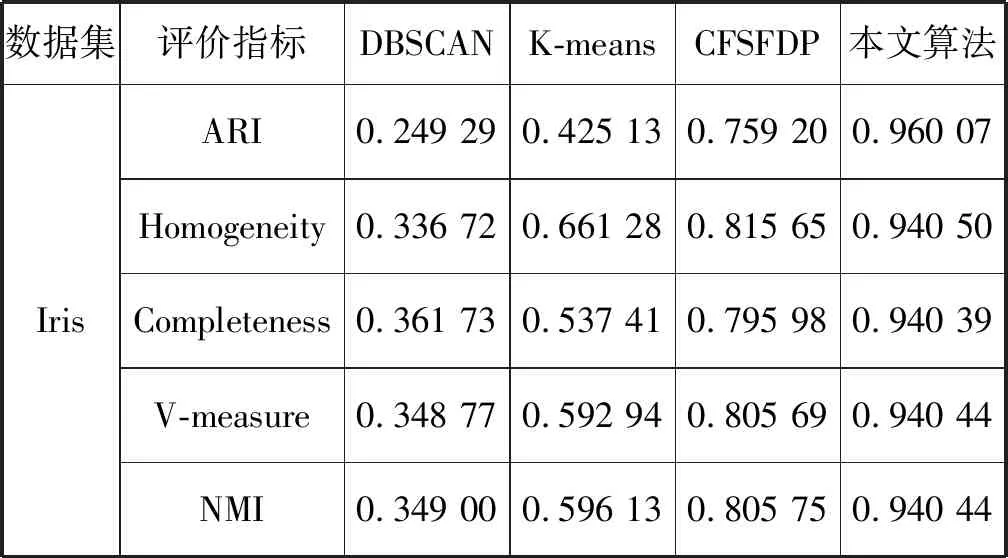
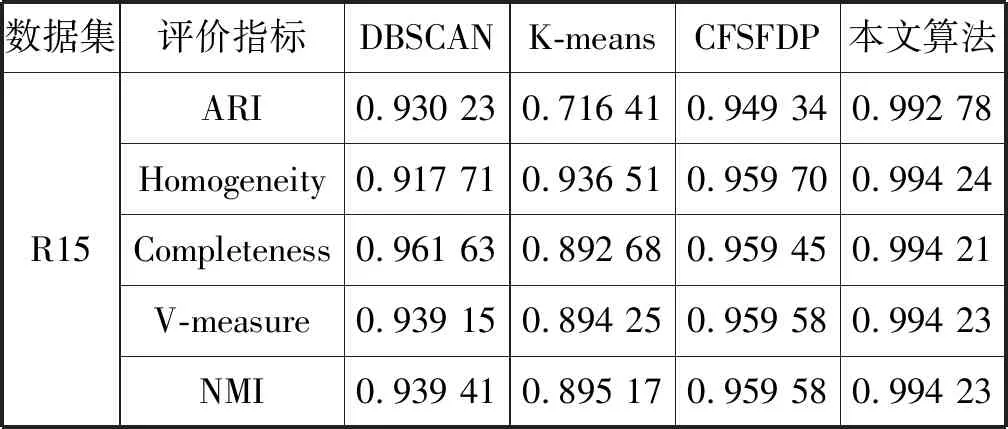
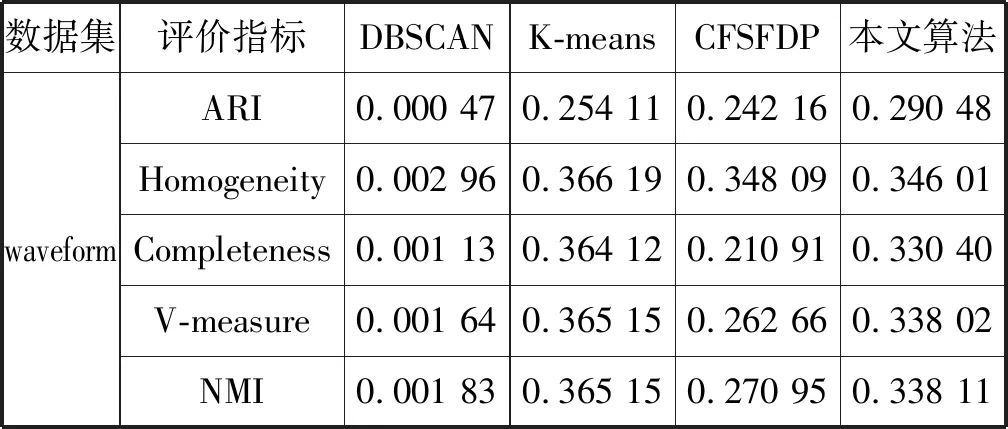
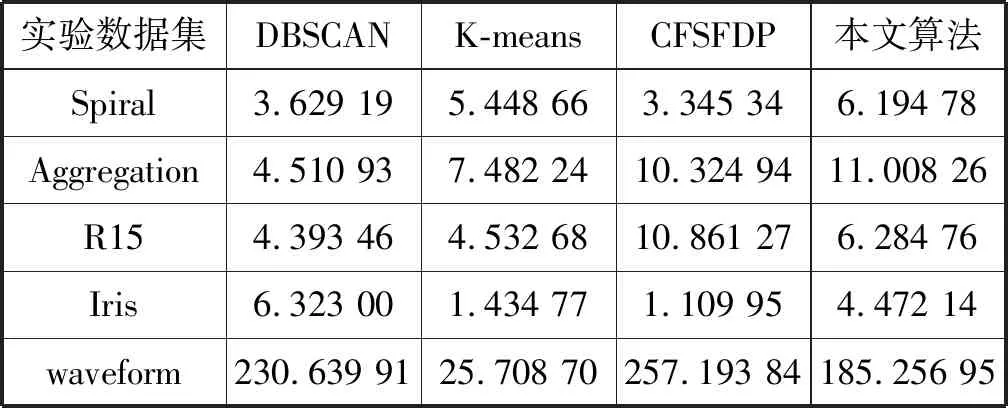
s.t.qj>qi,j 算法的具体实现步骤如下: 输入:数据集S={x1,x2,…,xN},截断距离参数dc 输出:数据集S各样本点的聚类结果 步骤: 1) 计算数据集S中任意两点间的距离矩阵; 2) 根据t(t=2)选择合适的dc; 3) 按照式(2)计算各样本点的局部密度ρ; 4) 根据式(3)计算各样本点的距离δ; 5) 把大于当前位置的多个密度值和最小距离各归为一个集合,只选择第一个点作为聚类中心; 6) 按照式(4)计算各样本点的γ值; 7) 利用各点降序排列的γ值分布图做决策图辅助图选取聚类中心数量; 8) 对非聚类中心点完成聚类,确定各点最终的归属。 本文提出的改进CFSFDP算法在保持原有算法寻找聚类中心的思想上,对γ函数进行了归一化处理,利用各数据点γ值的分布图做决策图辅助图,实现聚类中心个数的选取。并且为了防止簇的分裂,对于同一簇中存在多个密度峰值的簇,只选择第一个高局部密度点计算局部高密度最小距离,避免簇的分裂,也提高了聚类中心选取的准确率。 为了检验改进算法的聚类效果,本文利用人工数据集和UCI数据集进行数值模拟实验,分别对DBSCAN算法、k-means算法、CFSFDP算法和改进的CFSFDP算法的实验结果以聚类效果图和各聚类算法的调整兰德系数、互信息评分、同质性、完整性和V-measure等评价指标结果对比呈现改进性能。 实验软件和硬件环境是:CPU:Inter(R) Core(TM) i5-3470@ 3.20 GHz;操作系统:Windows10 64位,内存:4 GB;编程软件:Python 3。 这部分实验采用数据集Spiral和Aggregation,具体属性如表1所示。 表1 实验各数据集属性表 Spiral数据集分布较为特殊,呈环状分布,因此其对算法的参数设置十分敏感,图2是各算法对Spiral数据集的聚类效果图。由图2(a)可知DBSCAN算法因为对参数选取敏感,故其在聚类过程中产生了少量噪声点;图2(b)中K-means算法出现了混乱的聚类结果;图2(c)和2(d)所示的CFSFDP算法和改进的CFSFDP算法因为仅有一个参数,并且算法对参数的选取有一定鲁棒性,因此都产生了较好的聚类效果。 (a) (b) (c) (d)图2 Spiral数据集各算法聚类效果图 Aggregation数据集中有几个类簇距离较近,易产生簇的混乱。图3(b)和(c)分别为K-means算法和CFSFDP算法的聚类效果图,聚类效果不佳,CFSFDP算法由于利用决策图主观性地对聚类中心个数进行选择,导致聚类中心个数的错选,使得聚类结果出错;图3(a)和(d)所示,DBSCAN算法和改进的CFSFDP算法对数据集的聚类效果良好,尤其是改进的CFSFDP算法利用重新定义的γ函数值做决策图辅助图,实现了聚类中心的正确选取。 (a) (b) (c) (d)图3 Aggregation数据集各算法聚类效果图 实验采用人工数据集R15和UCI数据集Iris和waveform进行测试,数据的具体属性如表2所示。利用这些数据集主要对各算法的调整兰德系数、同质性、完整性、V-measure和标准互信息评分等评价指标的结果进行对比。 表2 实验各数据集属性表 设U为样本实际类别分配情况,V为样本聚类后的标签预测情况。各评价指标[15]定义如下: 1) 调整兰德系数: 2) 同质性: 3) 完整性: 4) V_measure: 5) 标准互信息评分: 上述公式中,ARI测量两个数据分布之间的一致程度,它具有高度的区分性,并且值范围是[-1,1]。V-measure是H和C的调和平均,取值范围为[0,1],常用来评估聚类模型的性能好坏。NMI是MI的标准化,用来衡量实际类别和预测类别的相似性,取值范围为[0,1],上述范围越接近于1说明聚类结果越好。实验结果如表3至表5所示。 表3 各算法在Iris数据集的各指标值对比 表4 各算法对R15数据集的各指标值对比 表5 各算法对waveform数据集的各指标值对比 Iris数据集是聚类分析中常用的数据集,由表3可知,本文改进的CFSFDP算法的各项评价指标都优于其他算法,并且ARI的指标值最好,高于0.95,DBSCAN算法的聚类效果最差,这是因为此数据集中存在样本分布稀疏的簇,使得DBSCAN算法将这些稀疏点作为噪声点处理,导致聚类精度较差。R15数据集中间的8个类簇距离很近,易造成簇混乱的情况,从表4的结果来看,改进的CFSFDP算法取得了较好的聚类结果,各项评价指标都很优,K-means算法中的k是需要提前指定的,k的随机选取易使得算法陷入局部最优,导致聚类结果不理想,造成各项评价指标最低。waveform数据集共21维,有5 000个样本点,是一个有着较高维度的大数据集,从表5的实验结果来看,改进的CFSFDP算法ARI指标值虽然是最好的,但是其他指标的值还是略低于K-means算法,但是远好于DBSCAN算法。 观察到改进CFSFDP算法对较高维度的大数据集聚类效果不理想,因此比较和分析各算法的时间复杂度,对上述实验各算法运行时间进行对比分析,结果如表6所示。 表6 各算法运行时间对比分析 s 从表6可以看出,改进CFSFDP算法虽然产生了较好的聚类效果,但是其算法运行时间略长于其他算法。这是由于其在具体计算中,需要对数据集中任意两点间的欧式距离进行计算,尤其是对维度较高的大数据集进行计算时,需要完成大量欧式距离的计算,还要完成数据集样本点局部密度和最小距离的计算,因此算法的时间复杂度至少为O(N2)。CFSFDP算法的时间复杂度是O(N2),K-means算法的时间复杂度为O(Nkt),DBSCAN算法的时间复杂度与数据集的维度有关,上界为O(N2)。 综上所述,改进CFSFDP算法的聚类性能整体上优于基本CFSFDP算法、K-means算法和DBSCAN算法,该算法非常适合于对较低维度数据集的聚类处理。 本文针对CFSFDP算法对单个簇中存在多密度峰值时聚类效果不理想的情况,提出将所有密度大于当前位置的数据点以及与当前位置的较近距离各做成一个集合,对局部密度进行排序,在存在多个密度峰值时只选择第一个点作为聚类中心,并且利用各数据点归一化的γ值分布图确定聚类中心数。通过数值分析发现,改进的CFSFDP算法适用于对任意形状特别是存在多密度峰值的较低维数据集的聚类。但是其算法运行时间还是略长,如何提升算法运行效率,尤其是对较高维度数据集的聚类将是下一步的研究重点。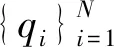
2.3 改进算法实现
3 数值模拟
3.1 聚类效果图

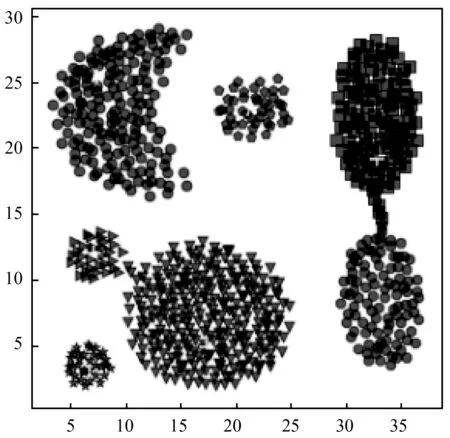
3.2 各聚类算法评价指标对比
3.3 各算法时间复杂度分析
4 结 语

