基于卷积神经网络模型的手写数字辨识算法研究

张 烁 张 荣

1(山西青年职业学院计算机系 山西 太原 030024)2(山西医科大学计算机教学部 山西 太原 030001)

0 引 言

手写数字辨识技术是指机器自动识别手写阿拉伯数字技术，是机器学习、模式识别等领域非常重要的一个研究方向[1]。1998年，LeCun等[2]提出了一种基于梯度学习的CNN算法(LeNet-5)，并应用于手写数字辨识中。鉴于此，LeNet网络当时应用于整个美国的邮政系统中，通过识别手写邮政编码来分类邮件。目前，在邮政编号识别、银行单据自动录入、财务报表自动录入等识别系统中，都使用了手写数字辨识技术[3]。近年来随着大数据和人工智能技术的快速发展，人们不但对手写数字的识别率提出了更高的要求，而且对算法训练模型的时间也提出了更高的要求[4]。

目前，手写数字辨识的方法[5]主要包括：结构识别法、统计识别法、深度学习法。结构识别法对相似数字有较强的识别能力，但是对于环境复杂的脱机数字识别往往识别正确率不高。统计识别法是指从大量的统计数据中提取出特征，然后通过决策函数进行分类。统计识别法通常有很强的抗干扰能力，但是往往识别的正确率也不理想。深度学习法的出现解决了识别率低的问题，并且通过改进深度学习网络加快模型的训练速度。在手写数字辨识问题领域，深度学习法是目前理想的选择。

卷积神经网络(CNN)是深度学习模型中最为成功的网络之一，并且在图像识别领域有很好的识别效果。深度学习(包括CNN、RNN等)是端到端的学习，传统机器学习往往通过模块化的方法解决此类问题，分为图像预处理、特征提取、设计分类器等子步骤完成任务。模块化的基本思想是：将一个复杂、繁琐的问题分成几个简单的子问题模块来处理。但是，在处理每个子问题时，每个子问题都可能存在最优解，将这些子问题组合起来后，从全局来看，并不一定会得到最优解。对于深度学习是基于端到端的深层次网络学习方式，整个流程并不进行子模块的划分，可以直接将原始数据输入到模型中，整个学习过程完全交给深层次网络模型，这样最大的优点就是可以统筹全局获得最优解。

1 网络模型结构设计

1.1 卷积神经网络

卷积神经网络由输入层、卷积层、池化层、全连接层、输出层构成，多个层可以看成一个复杂的函数fCNN，损失函数由参数正则化损失和数据损失构成，在训练整个网络时，按照损失函数将参数误差反向传播给整个模型的各个层次，达到参数更新的目的。整个训练过程可以看成从原始数据向最终目标的直接拟合，中间各层次的作用为特征学习。CNN原理图如图1所示。可以看出，卷积层和池化层是整个CNN网络的核心。

在卷积层中，通过可训练的卷积核对上一层的输入数据进行卷积操作，通常卷积核为3×3或5×5的矩阵，确定大小的卷积核按照规定的步长在上一层输入数据做从左到右、从上到下的“滑动”操作，并输出特征图，每次卷积操作都可以提取出一种特征。如果在CNN网络训练时有n个卷积核就可以提取出图像的n个特征。一般地，若一个三维张量xk为第k卷积层的输入，满足xk∈RHk×Wk×Dk，该层的卷积核为wk∈RH×W×Dk，卷积核有D个，则在同一数据位置上可以得到D维的卷积输出，即在k+1层的特征矩阵输入xk+1的通道数为D，可表示为：

(1)

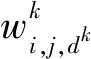
在池化层中，主要的任务是对上一层特征图进行下采样处理，这是一种采样较少的数据还保持原有重要信息的一种操作。常用的池化操作类型[6]分为平均池化(Average-Pooling)、最大池化(Max-Pooling)等。平均池化是在每次数据操作时，将池化核覆盖区域的数值取平均值，可表示为：

(2)

最大池化是在每次对数据操作时，将池化核覆盖区域的数据取最大值，可表示为：

(3)

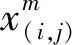
如图1所示，卷积层和池化层通常交替设置，图像数据每经过一次卷积层和池化层后，都会提取出图像特征。随着交替次数的增大，提取的图像特征逐步由低级特征到高级特征，最终形成对图像的特征描述。最后通过CNN网络的一个或多个全连接层输出分类结果。

1.2 卷积神经网络设计

本文设计的CNN网络有8层构成，分别是1个输入层、2个卷积层、2个池化层、2个全连接层、1个输出层。除去整个网络的输入层和输出层，中间的2个卷积层、2个池化层、2个全连接层可以看成网络的隐含层。CNN网络结构如图2所示。

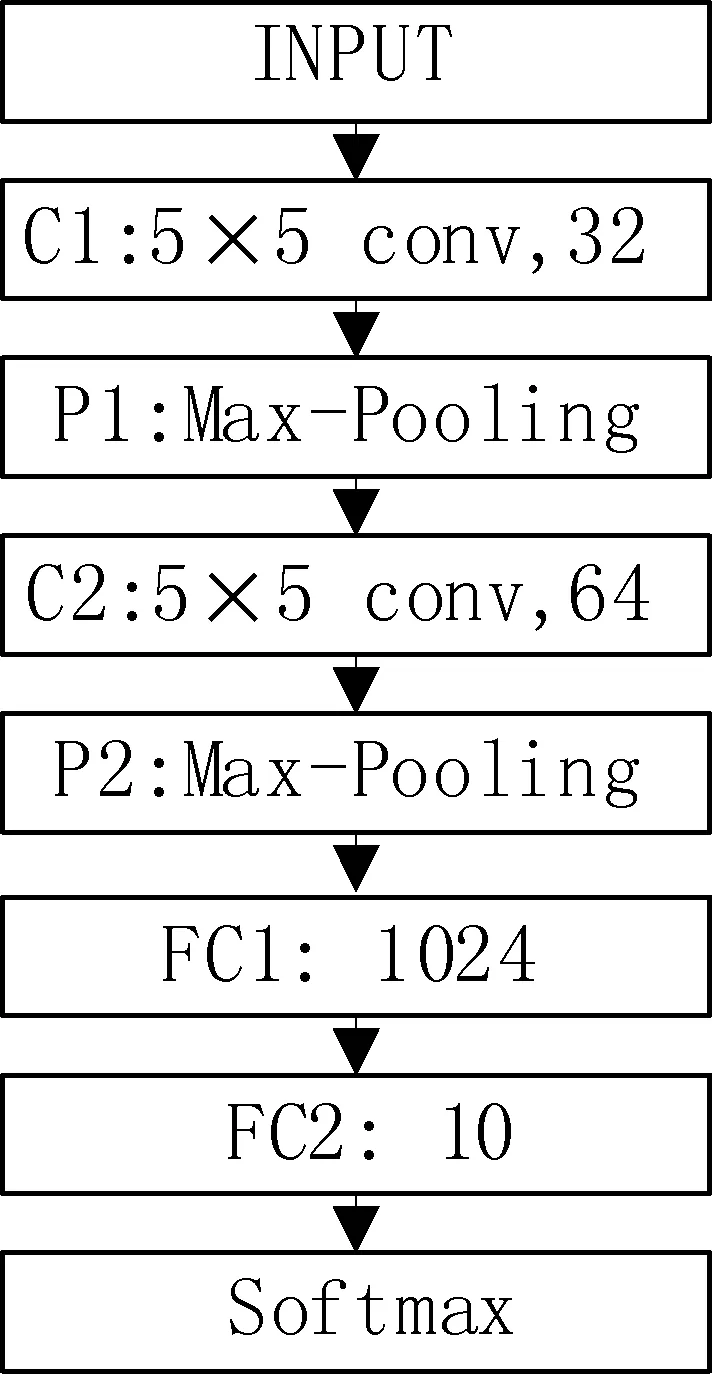
图2 CNN网络结构图

本文设计的CNN网络结构中，输入层INPUT包含28×28×1个神经元。C1层为卷积层，卷积核大小为5×5，32个卷积通道数，每个通道为14×14的矩阵。P1为池化层，包括32个池化通道，每个通道为14×14的矩阵，每个池化通道是由C1层经过大小为2×2、步长为2的最大池化后，通过ReLU激活函数进行非线性变化得到的。C2为卷积层，包括64个卷积通道数，每个通道为7×7的矩阵。P2为池化层，包括64个7×7的池化通道。每个池化通道是由C2层经过大小为2×2、步长为2的窗口进行最大池化后，通过ReLU激活函数进行非线性变化得到的。FC1为全连接层，有1 024个神经元，每个神经元和P2层的每个神经元相连接。FC2为全连接层，有10个神经元，每个神经元和FC1层的每个神经元相连接。最后通过SoftMax函数输出分类结果。

2 改进的CNN网络模型算法原理

2.1 学习率改进

一个理想的学习率要求一开始学习率的数值较大，并且有较快的收敛速度，然后随着迭代次数的增加，学习率的数值慢慢衰减，最后达到最优解。本文设计的CNN网络模型定义一个学习率适应这样的过程，在实现批量随机梯度下降法时，实现学习率的指数衰减。学习率指数衰减η(t)公式如下：

(4)

式中：η0为学习率初始值；t为迭代次数；r为衰减率。

2.2 Dropout正则化方法

为了减少全连接层网络的复杂程度，本文设计的CNN网络使用Dropout正则化方法。传统的神经网络中，每个神经元之间相互联系，每一个神经元都会反向传导后一个神经元的梯度信息并且相互之间联系紧密，增加了网络训练的复杂度。Dropout可以降低神经元之间的紧密性和相互依赖，来提高算法的“泛化能力”，防止发生“过拟合”现象。

Dropout的原理是：在训练时，对于网络每一层的神经元，以p为概率随机地丢掉一些神经元，也就是将这些神经元的权值w设为0；在测试时，将所有的神经元都设为激活状态，但需要将训练时丢掉的神经元权值w乘以(1-p)来保证训练和测试阶段各自权值有相同的期望。具体如图3所示。

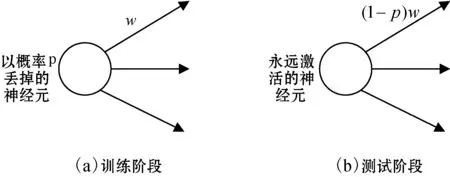
图3 单个神经元的Dropout

2.3 参数优化方法

本文在训练CNN网络时，使用了不同的参数优化方法来比较各个参数优化方法在训练手写数字图像的性能。

(1) 批量随机梯度下降法(mini-batch based SGD)SGD在进行样本训练时，在每一轮的训练过程中，不对全部样本进行训练，只是随机的选择一个样本进行训练，这样可以提高收敛速度。SGD可以分批计算训练集的代价函数并用梯度对θ参数进行更新公式如下：

θ←θ-η·▽f(θ,xi,yi)

(5)

式中：f(θ,xi,yi)为代价函数；▽f(θ,xi,yi)是随机选取样本空间(xi,yi)的一点对θ的梯度；η为学习率。

(2) Momentum算法 Momentum算法借助了物理中动量的概念，模拟了运动物体时的惯性，在参数更新的时候在一定程度上保留了之前更新的方向，可以增加稳定性并且有较快的学习速度，θ参数更新公式如下：

vt=γ·vt-1+η·▽f(θ,xi,yi)

(6)

θ←θ-vt

(7)

式中：γ为动量；vi为i时的梯度变化。

(3) Adagrad算法 Adagrad算法的最大特点是可以在训练时对学习率进行动态调整。当参数出现的频率较低时，采用较大的学习率进行参数训练；相反，参数出现的频率较高时，采用较小的学习率进行参数训练。在处理稀疏数据时，Adagrad算法有较好的训练效果。θ参数更新公式如下：

(8)

式中：Gt为对角矩阵每个位置参数对应从第1轮训练到第t轮训练梯度的平方和；ε为平滑项，防止分式的分母为0，一般取值为1e-8。

(4) RMSprop算法 RMSprop算法是人工智能大师Hinton提出的一种自适应学习率动态调整算法，其目的是为了缓解Adagrad算法中学习率下降过快。Adagrad算法会累加之前所有的梯度平方，而RMSprop算法是计算之前所有梯度的平均值。θ参数更新公式如下：

(9)

式中：Et为对角矩阵每个位置参数对应从第1轮训练到第t轮训练梯度的均值。

(5) Adam算法 Adam算法也是一种学习率自适应算法，它利用梯度的一阶矩阵和二阶矩阵来动态调整参数的学习率。其最大的优点是校正的学习率，使每一次迭代都有一个确定的范围，并且使参数更新比较平稳。θ参数更新公式如下：

(10)

式中：vt和mt分别是对代价函数求梯度的一阶矩阵和二阶矩阵。

2.4 算法流程

基于本文提出的CNN模型训练参数时，主要包括使用动态学习率，在网络训练时加入了Dropout方法和分别使用了批量随机梯度下降法、Momentum算法、Adagrad算法、RMSprop算法、Adam算法进行参数优化。算法整体流程图如图4所示。

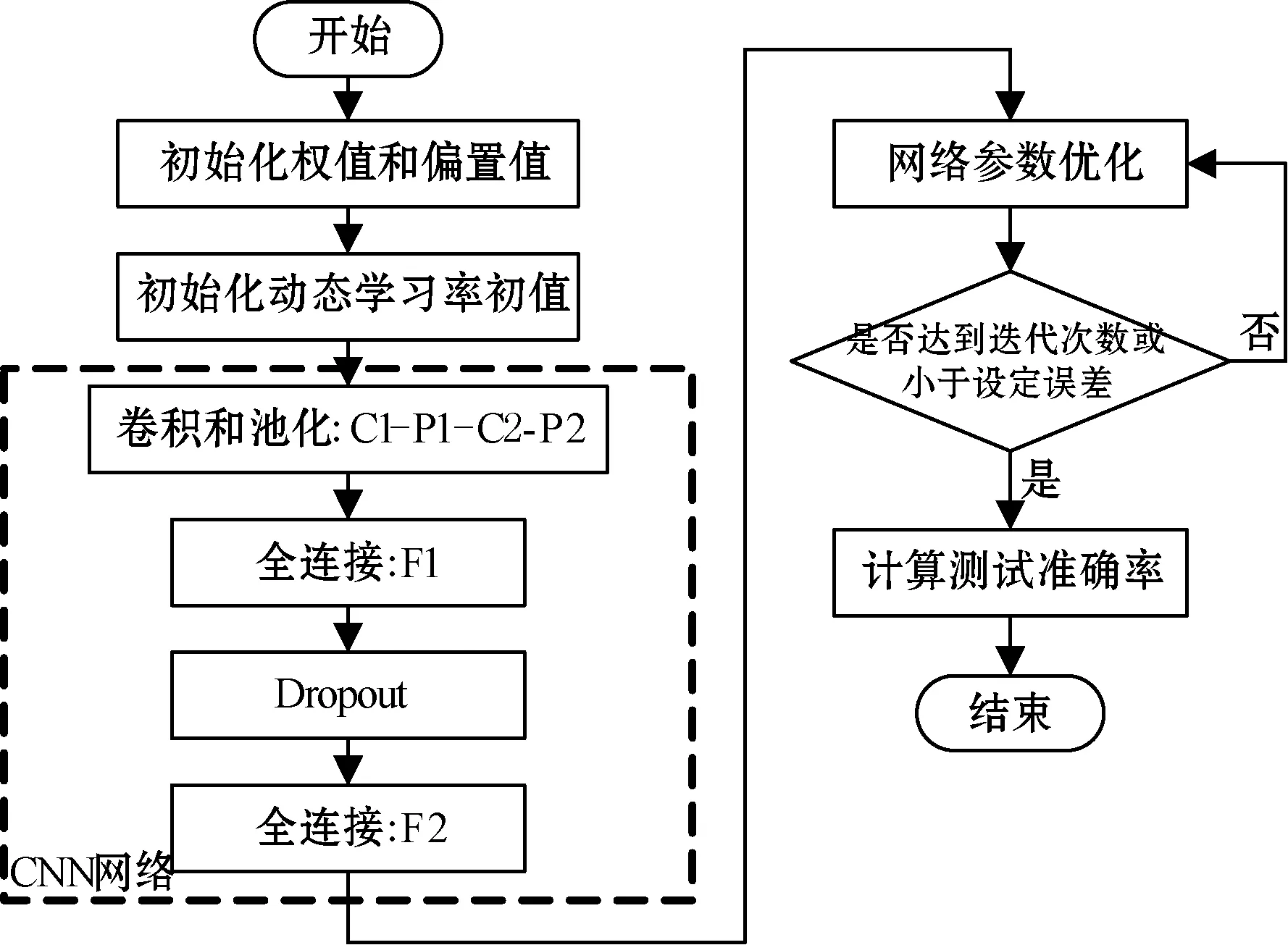
图4 参数训练算法流程图

3 实验与结果分析

3.1 实验数据集与仿真环境

仿真实验所用的数据集是美国国家标准与技术研究所编制的MNIST数据集，该数据集有含有0～9的手写数字图像，其中训练集有60 000个样本图像，测试集有10 000个样本图像，训练集数据标签是“one-hot vector”形式，每张图像大小为像素。每次训练数据时，批次的大小为50，训练的迭代次数为101次，分别使用了本文提及的5种参数优化方法进行训练。仿真实验硬件环境为Windows 8操作系统，第八代i7处理器3.60 GHz，16 GB内存，GeForce 1080Ti独立显卡；软件环境为TensorFlow 1.4+Python 3.6。

3.2 实验数据测试

本文是基于TensorFlow开源框架来构建CNN网络模型实现手写数字辨识的训练过程，其CNN网络模型参数具体配置如表1所示。

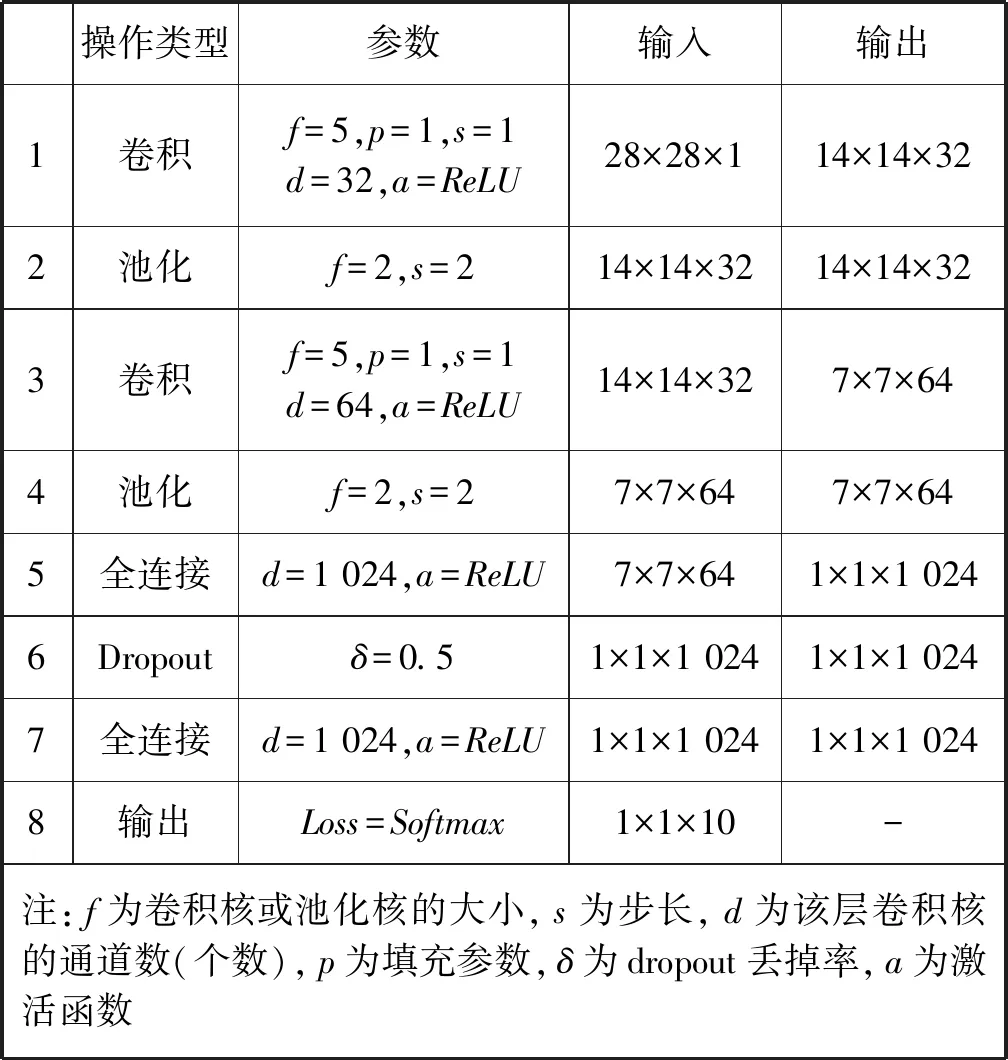
表1 本文CNN网络模型参数

使用批量随机梯度下降法和表1的CNN网络模型参数配置来优化参数，学习率为动态指数衰减方式，实验分析包括测试集准确率、训练集代价函数错误率、迭代次数、训练时间。如图5所示，在训练数据时，代价函数经过101次迭代后错误率为1.80%，但是测试集准确率只为75.60%，整个训练时间为14 min 33 s。这说明使用批量随机梯度下降法来优化参数时，整个网络模型的泛化能力不强，发生了过拟合现象。

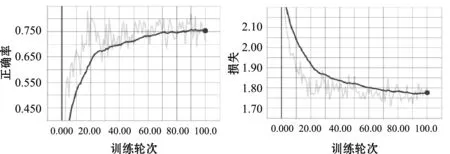
(a) 测试集正确率 (b) 训练集错误率图5 批量随机梯度下降法训练CNN网络模型

分别使用Momentum算法、Adagrad算法、RMSprop算法、Adam算法对网络参数进行优化来比较各个算法性能，如图6和图7所示。

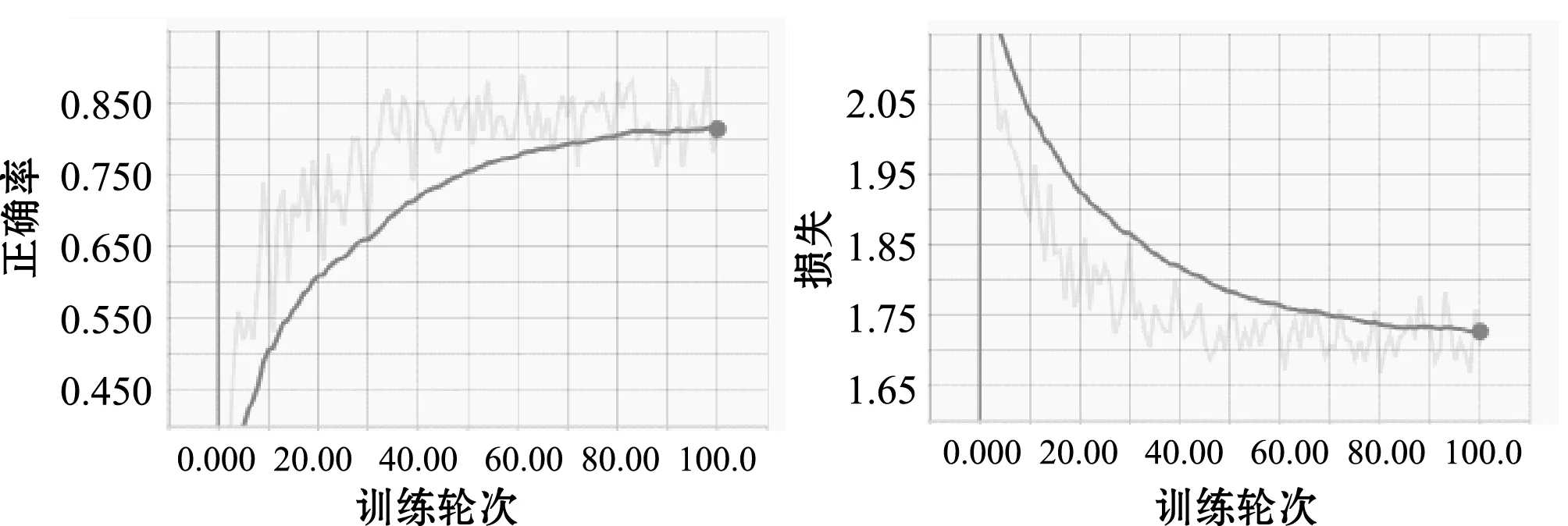
(a) Momentum优化 测试集正确率 (b) Momentum优化训练集错误率

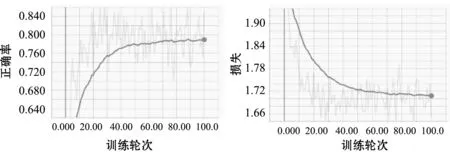
(c) Adagrad优化 测试集正确率 (d) Adagrad优化训练集错误率图6 Momentum算法和Adagrad算法训练CNN网络模型

(c) Adam优化测试集正确率 (d) Adam优化训练集错误率图7 RMSprop算法、Adam算法训练CNN网络模型

通过图6可以看出，Momentum算法和Adagrad算法在训练数据时，训练集经过101次训练后错误率分别为1.70%和1.72%，但是测试集的准确率分别只有79.29%和82.20%，并且收敛速度较慢。训练时间分别为15 min 20 s和15 min 13 s。从图中可以看出Adagrad算法在训练时震荡剧烈。

通过图7可以看出，RMSprop算法和Adam算法在训练数据时，训练集经过101次训练后错误率分别为1.46%和1.47%，在测试集的准确率分别为99.40%和99.70%，训练时间分别为15 min 58 s和15 min 42 s。这两种算法在迭代次数较小的情况下，就已经达到较高的准确率，说明收敛速度较其他算法快。可以看出，使用RMSprop算法和Adam算法在测试集的准确率远远高于其他优化器算法，并且Adam算法比RMSprop算法的准确率高出0.3%，训练时间少16 s。

各优化器算法总结如表2所示。

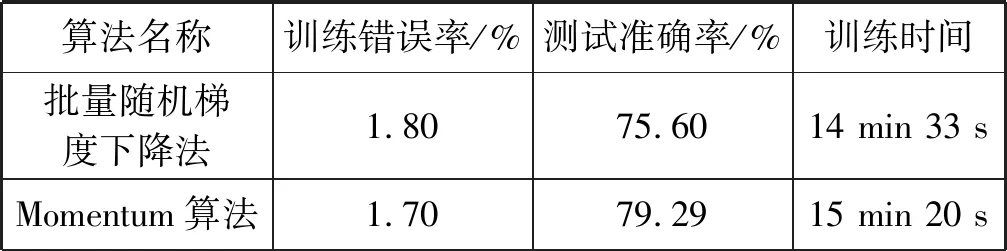
表2 各优化器算法比较

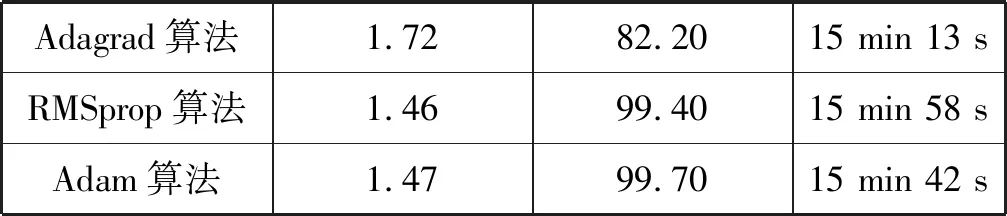
续表2

为了分析本文CNN网络在测试集的识别性能，将识别准确率与其他手写数字识别方法进行比较，如表3所示。

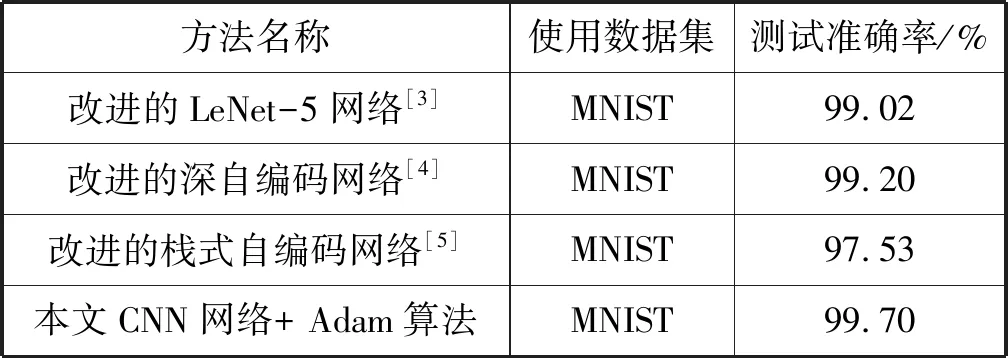
表3 几种手写数字识别方法比较

综上所述，基于本文设计的CNN网络结构， Adam算法在训练集的错误率、测试集的准确率和收敛速度方面都优于其他优化器。各优化器在训练集的错误率都较低，但使用批量随机梯度下降法、Momentum算法和Adagrad算法验证测试集准确率都表现不佳，说明这三种算法在优化网络参数时，泛化能力不强。批量随机梯度下降法参数优化时间最短，但是测试准确率最低；RMSprop算法训练时间最长，测试准确率可以达到99.40%。所有算法训练时间都在可接受范围之内，并且与机器的配置有很大关系。基于本文设计的CNN网络和Adam参数优化算法在相同数据集的情况下，测试集准确率高于文献[3-5]中数字识别方法的准确率。

4 结 语

本文基于手写数字辨识对CNN网络模型参数优化进行研究。实验结果表明：在本文设计的CNN网络模型下，使用学习率动态衰减、Dropout正则化方法，RMSprop算法和Adam算法在参数优化方面收敛速度快、识别准确率高，测试集准确率可达99.40%和99.70%。下一步将优化CNN网络模型，可将优化的CNN网络模型使用RMSprop算法和Adam算法优化参数的方法应用在其他图像识别中。