车站运行列车异音检测方法
张宏睿 马秀荣 单云龙
(天津理工大学电气电子工程学院 天津 300384)
0 引 言
铁路、公路、航空、水路和管道是现代交通系统的五大运输方式。相比较其他运输方式,铁路有着天然的优势,一是能源消耗少,二是对环境污染小,三是运输能力强。伴随着铁路运输的飞速发展,铁路列车在高速度和高强度条件下运行时,自身的安全问题也越来越受到人们的关注,任何存在的安全隐患都可能会造成重大铁路交通事故。
异音检测是指以声学诊断的方式对列车运行音频进行识别,检测出列车非正常运行的声音。其目的在于及时发现列车运行过程中危及行车的安全隐患,实时进行列车故障定位、及时故障预警,以便铁路工作人员能针对故障及时处理,确保铁路运输安全[1-7]。
列车行车音频信号存在低信噪比、多噪声源、噪声变化大的特点,挑选合理的降噪方法[8-18],尽量降低背景环境噪声对特征值提取的影响是提高车站运行列车异常声音检测准确率的关键。本文对传统MCRA噪声估计算法作出了改进。在最小值搜索之前先对含噪音频功率谱的每一个频点进行非线性平滑,然后用一个一阶差分运算进行最小值搜索,从而连续地实时更新估计噪声谱。通过最小值统计(minimum statistics,MS)算法、传统MCRA算法、改进的MCRA算法估计出的噪声谱与实际噪声谱的仿真分析,证明了改进算法的优越性。
除了降低环境噪声的干扰,异音检测的另一个技术难点在于异常特征的有效提取识别。针对无法提取纯净列车行车信号且异常行车样本少、异常特征类型多的的特点,传统的能熵比检测法、子带能熵比检测法等时频分析方法并不能有效提取异常特征。本文采用改进能熵比[19-21]的方法,对应不同异常频段进行异常检测,有效提高了异常识别的准确率。
1 车站运行列车的异音检测方法
本文所述异音检测方法流程图如图1所示,关键步骤主要包括:(1) 改进的噪声估计方法;(2) 改进的降噪方法;(3) 车头车厢分离方法;(4) 改进的异常类型判别方法。
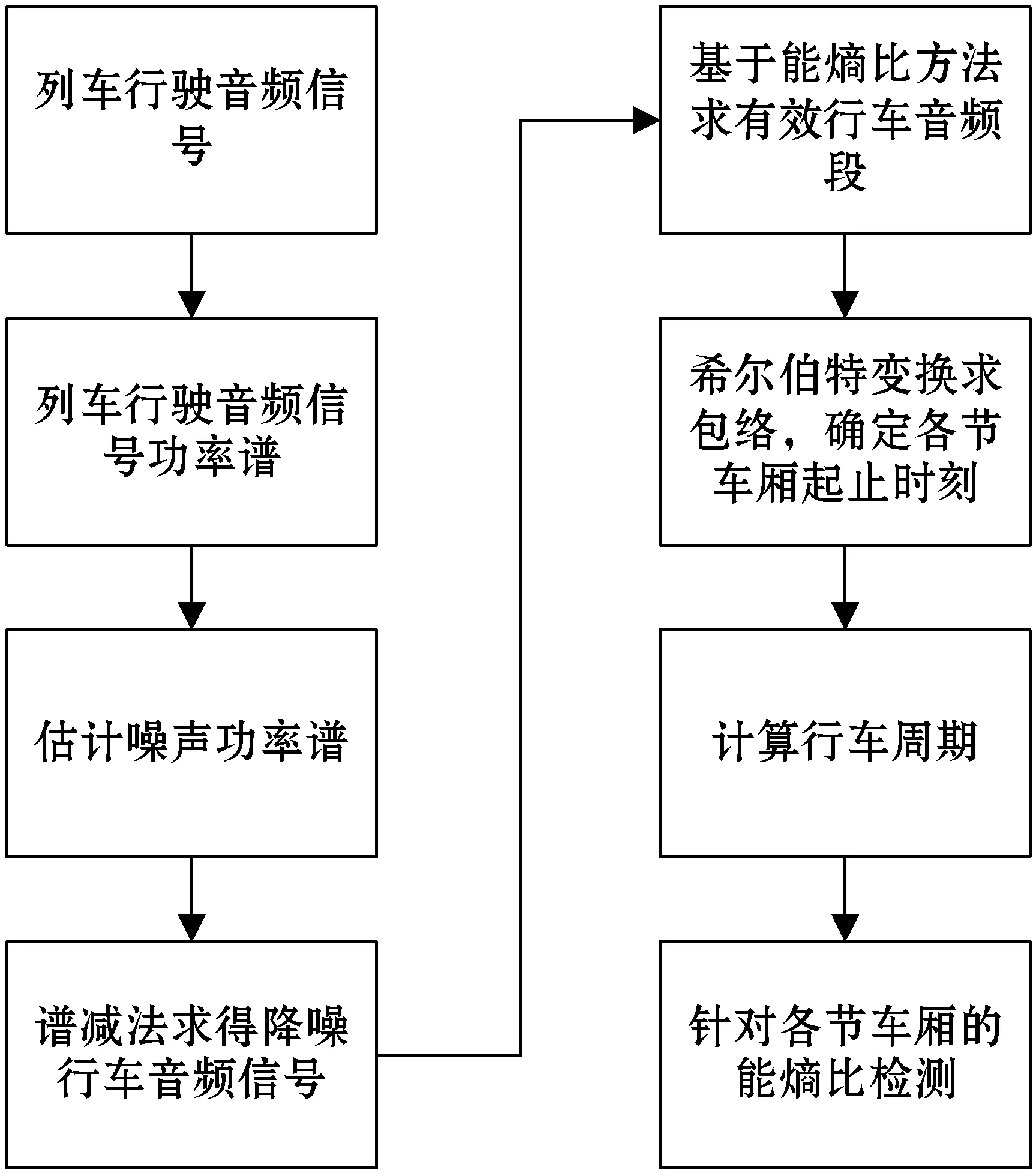
图1 异音检测方法流程图
噪声估计步骤实现了行车噪声谱的实时估计,通过估计出的噪声谱用改进的谱减法做降噪处理;对降噪后的音频做能熵比端点检测,识别有效行车音频段;用希尔伯特变换求有效行车音频的时域包络,由包络谷值确定各节车厢的起止时刻;通过相邻波谷的时间差值确定列车车厢的平均行驶周期,按周期分割每节车厢的音频;分别对每节车厢的音频做改进的能熵比检测,判别车厢的行驶状况。通过上述步骤,能够及时有效识别定位异常行车车厢的位置以及异常类型,确保列车的安全行驶。
2 异音检测方法关键步骤介绍
2.1 改进的最小值控制的递归平均算法
2.1.1最小值控制的递归平均算法(MCRA)
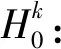
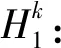
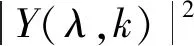
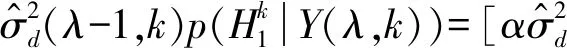
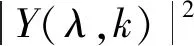

式中:
αd(λ,k)=α+(1-α)p(λ,k)
(4)
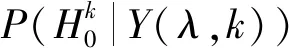
带噪音频功率谱的平滑估计为:
S(λ,k)=αsS(λ-1,k)+(1-αs)Sf(λ,k)
(5)
式中:αs=0.7是平滑因子。
式中:w(i)为窗函数,使用汉明窗,窗长为2Lw+1。
搜索平滑目标信号功率谱局部最小值Smin(λ,k),Smin(λ,k)通过在一个D帧的固定窗口上与过去每一个S(λ,k)进行对比得到:
式中:Stmp(λ,k)为临时变量,Smin(0,k)=S(0,k),Stmp(0,k)=S(0,k)。以上算法每帧每个频点只需做一次运算比较,带噪音频的最小值从D个连续帧中寻找。噪声增大情况下,最小值搜索会有2D帧的延迟。
S(λ,k)与Smin(λ,k)的比值为:
将该比值与阈值δ比较,判断出目标信号存在的频段,即:
式中:δ=5。p(λ,k)=1时,目标信号存在;p(λ,k)=0时,目标信号不存在。最后估计目标信号存在的条件概率:
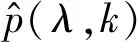
2.1.2改进的最小值控制的递归平均算法
假设目标信号存在期间,带噪音频信号功率最低会衰减到噪声功率水平。通过跟踪带噪音频每一帧的最小值,可以得到一个噪声水平的粗略估计。当平滑因子αs接近于1时,估计的带噪音频功率谱更加平滑,导致峰值变得更宽,频谱中一些细小的波动被消除。过度的平滑有可能导致噪声估计的不准确,因为最小值有可能落到拓宽后的谱峰之内,进而高估了实际噪声。理想情况下,在目标信号存在期间平滑参数较小,以更好地跟踪目标信号的非平稳段。如图2所示,可清楚地看出2.5 s处估计的噪声谱随着αs的增大而更大。
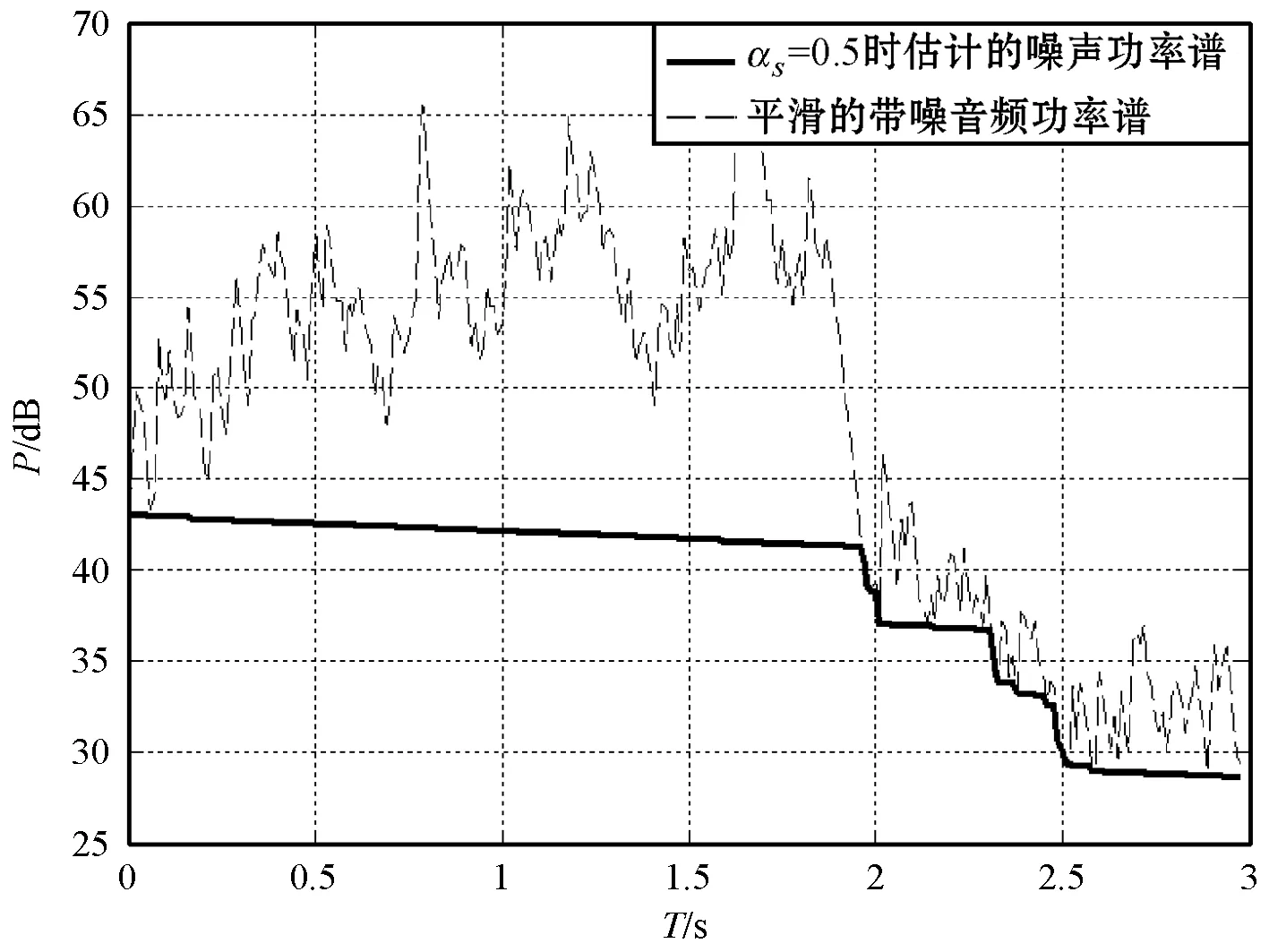
(a) αs=0.5
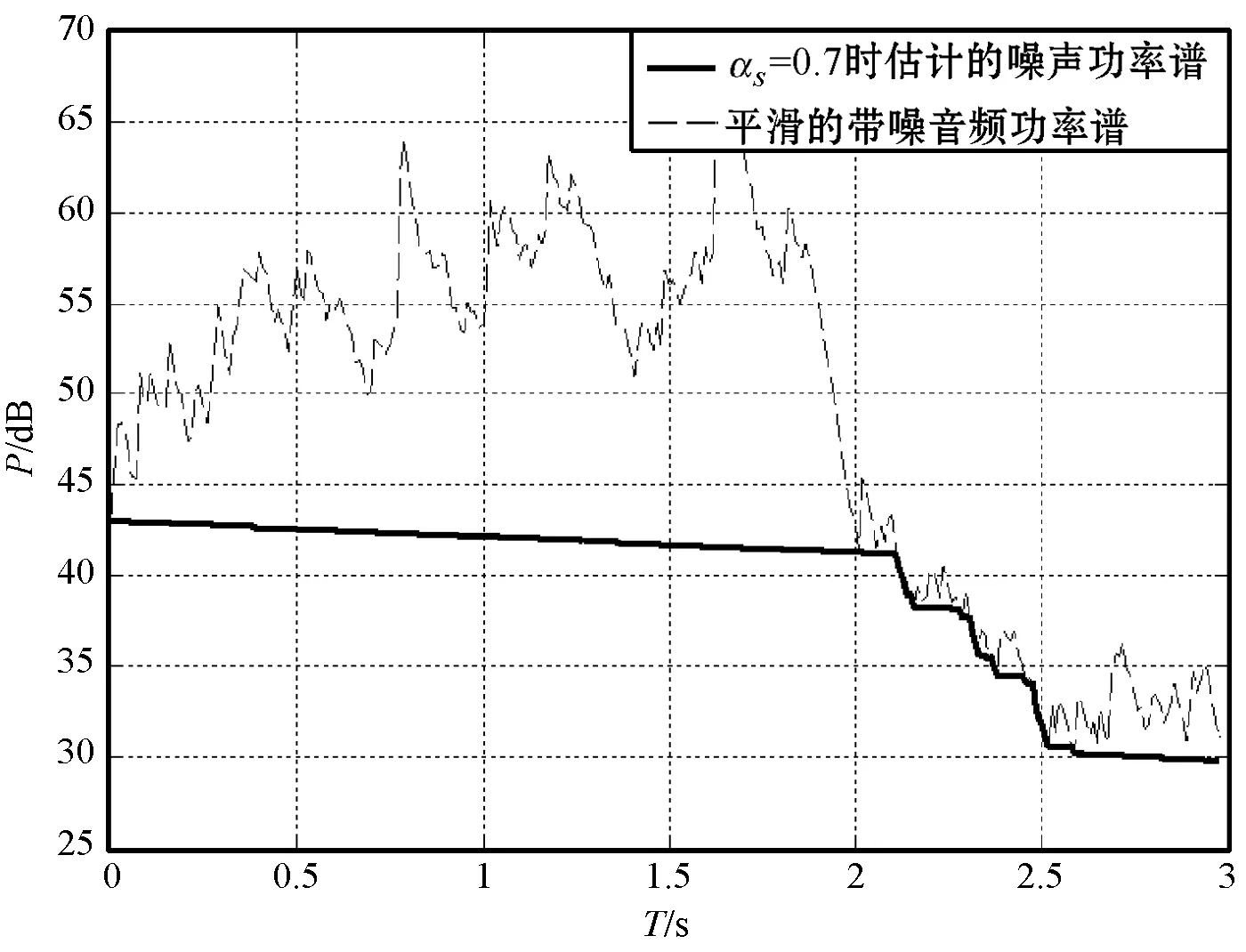
(b) αs=0.7
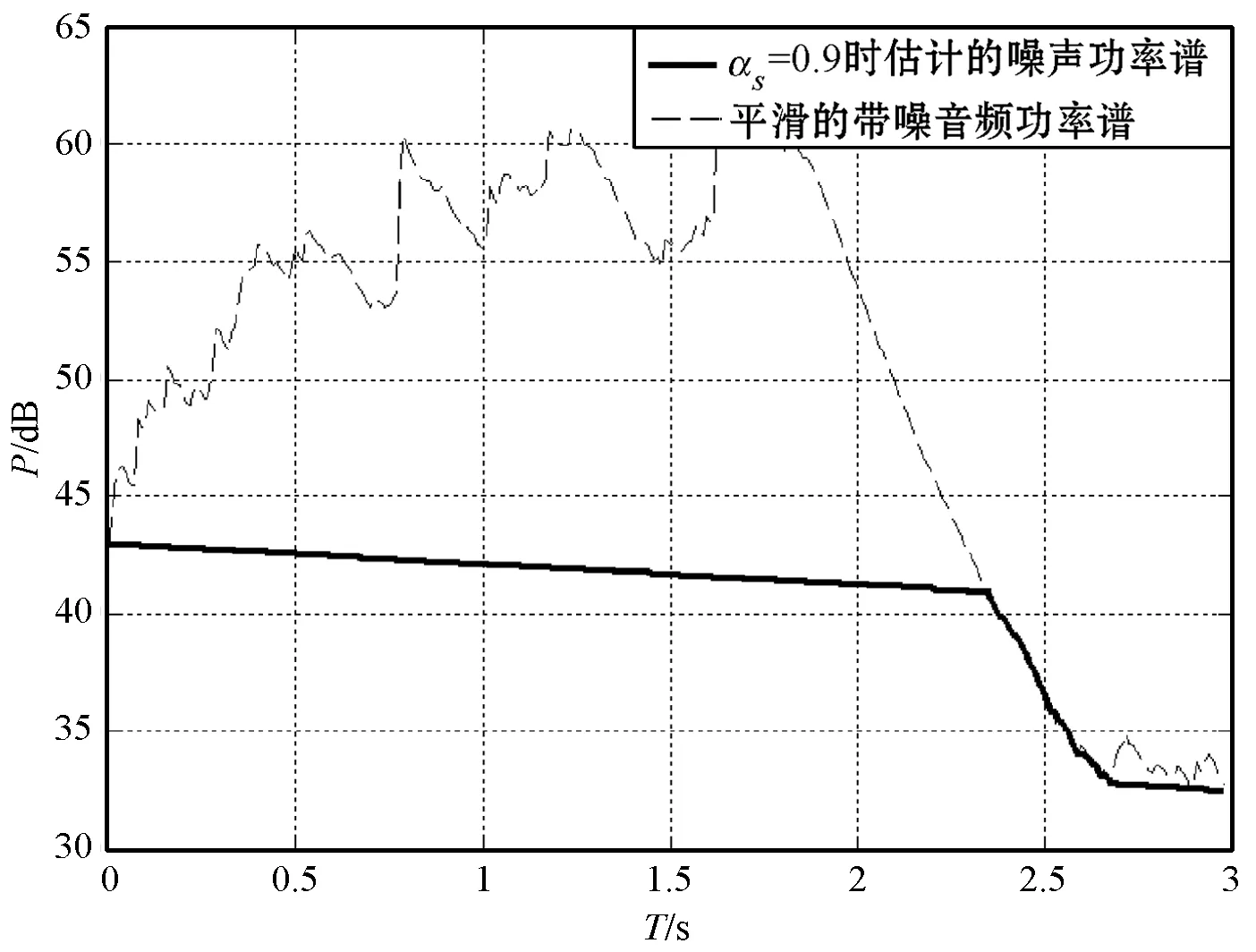
(c) αs=0.9图2 采用三种不同的αs的谱最小值(k=1 700 Hz)
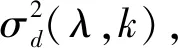
式中:
S(λ,k)=αs(λ,k)S(λ-1,k)+

令误差方程关于αs(λ,k)的一阶导数等于零,得到最优平滑因子αopt(λ,k):
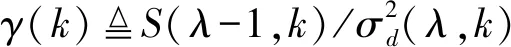
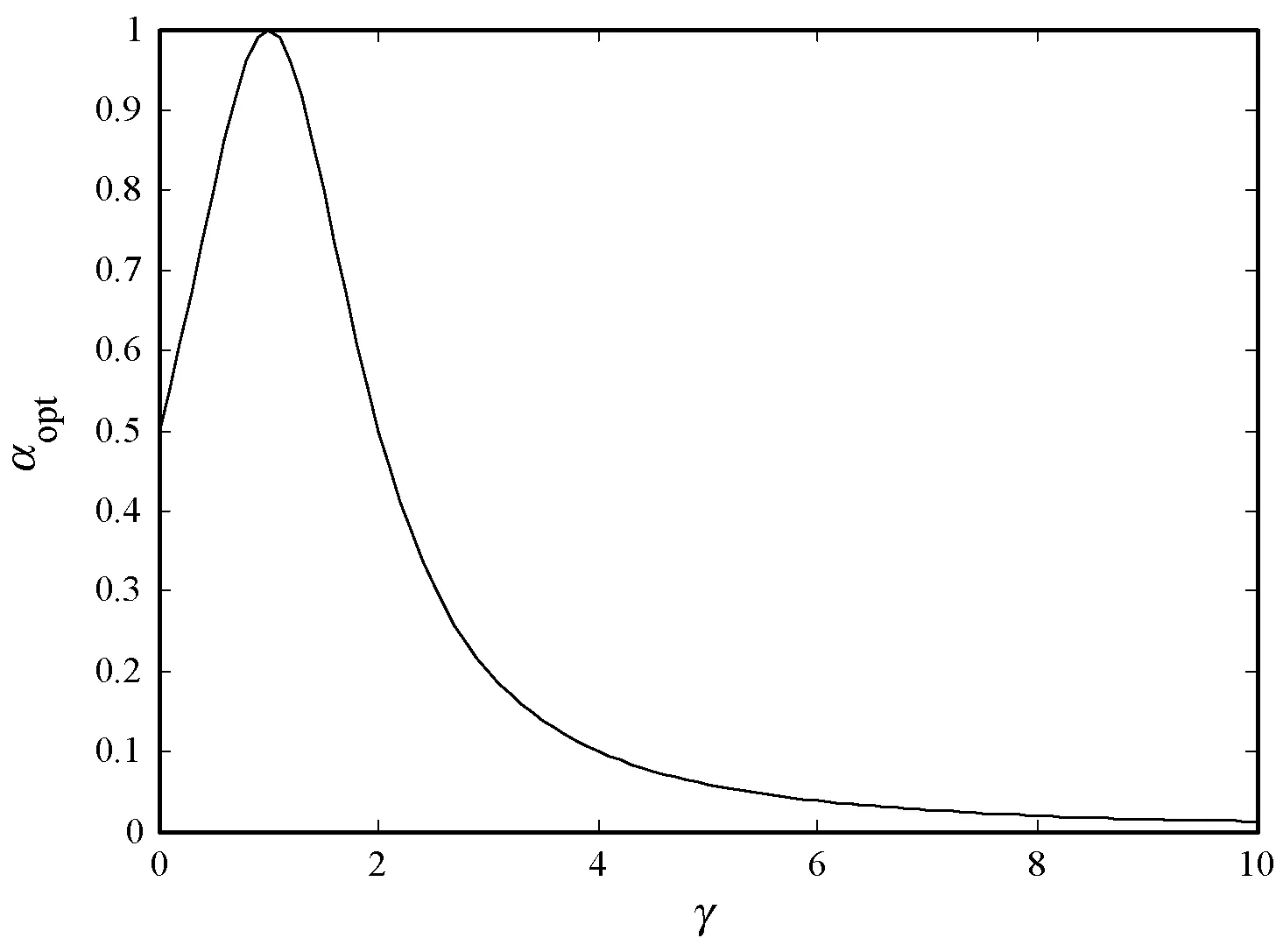
图3 αopt(λ,k)曲线
由图3可知,在目标信号存在时,随着γ(k)的增大,αopt(λ,k)迅速减小,这一特性有利于更好地跟踪功率谱密度变化。
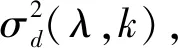
(16)
最终的平滑参数包含以上的校正因子αc(λ)并限制了其最大值αmax,表示如下:
(17)
式中:αmax=0.96以避免当γ(k)=1时出现死锁。
另外,传统MCRA算法噪声估计算法得到的噪声功率谱估计相对于实际噪声功率谱可能会有多达2D帧的延迟。改进Smin(λ,k)的跟踪方法为:
(18)
参数设置为:β=0.96,γ=0.998。以上过程在追踪最小值时使用一个“前瞻”因子β,通过调整该因子可以改变算法的自适应时间。
整体的噪声估计流程图如图4所示。
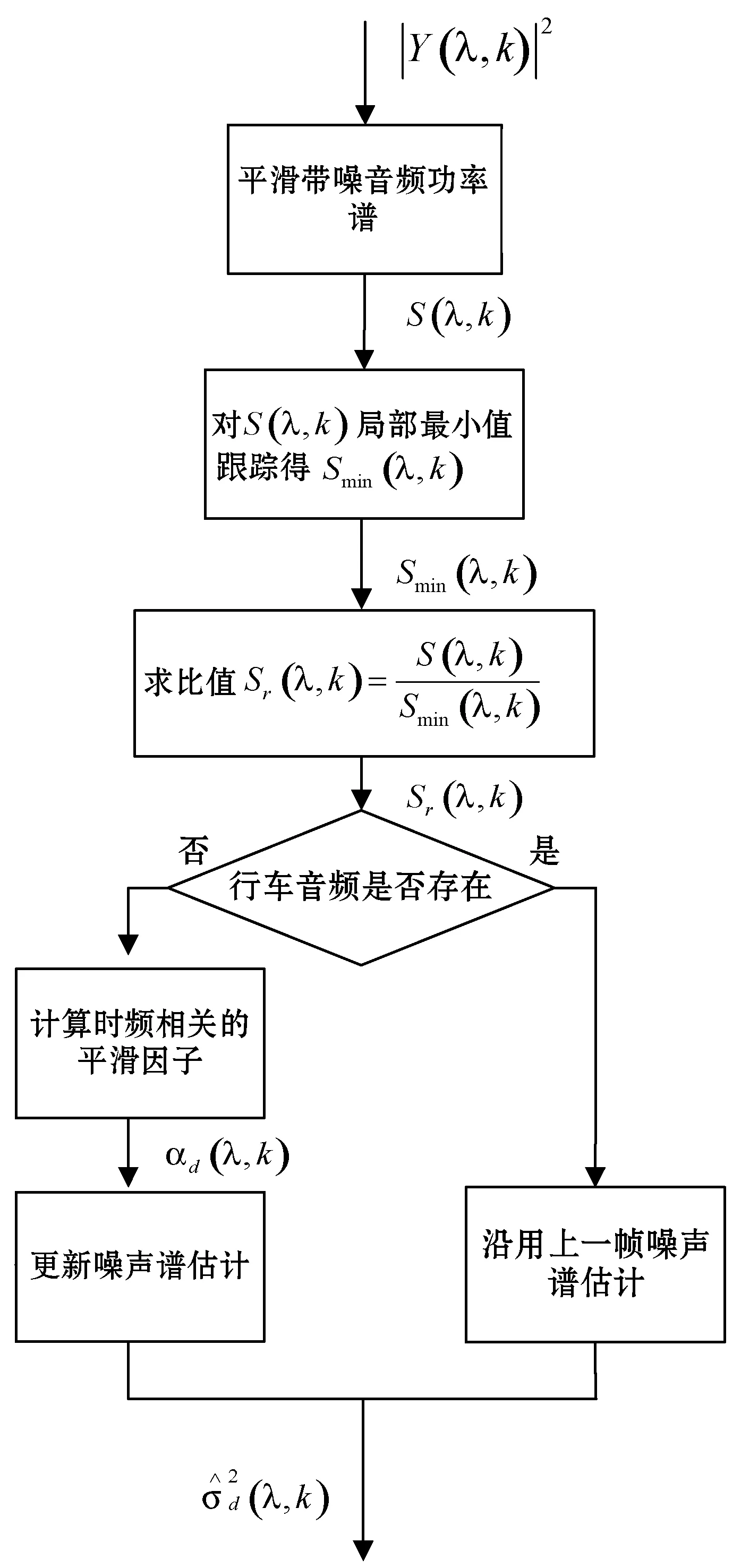
图4 噪声估计流程图
图5比较了采用本文改进算法、MS算法以及MCRA算法估计出的噪声功率谱与真实噪声谱的差异。
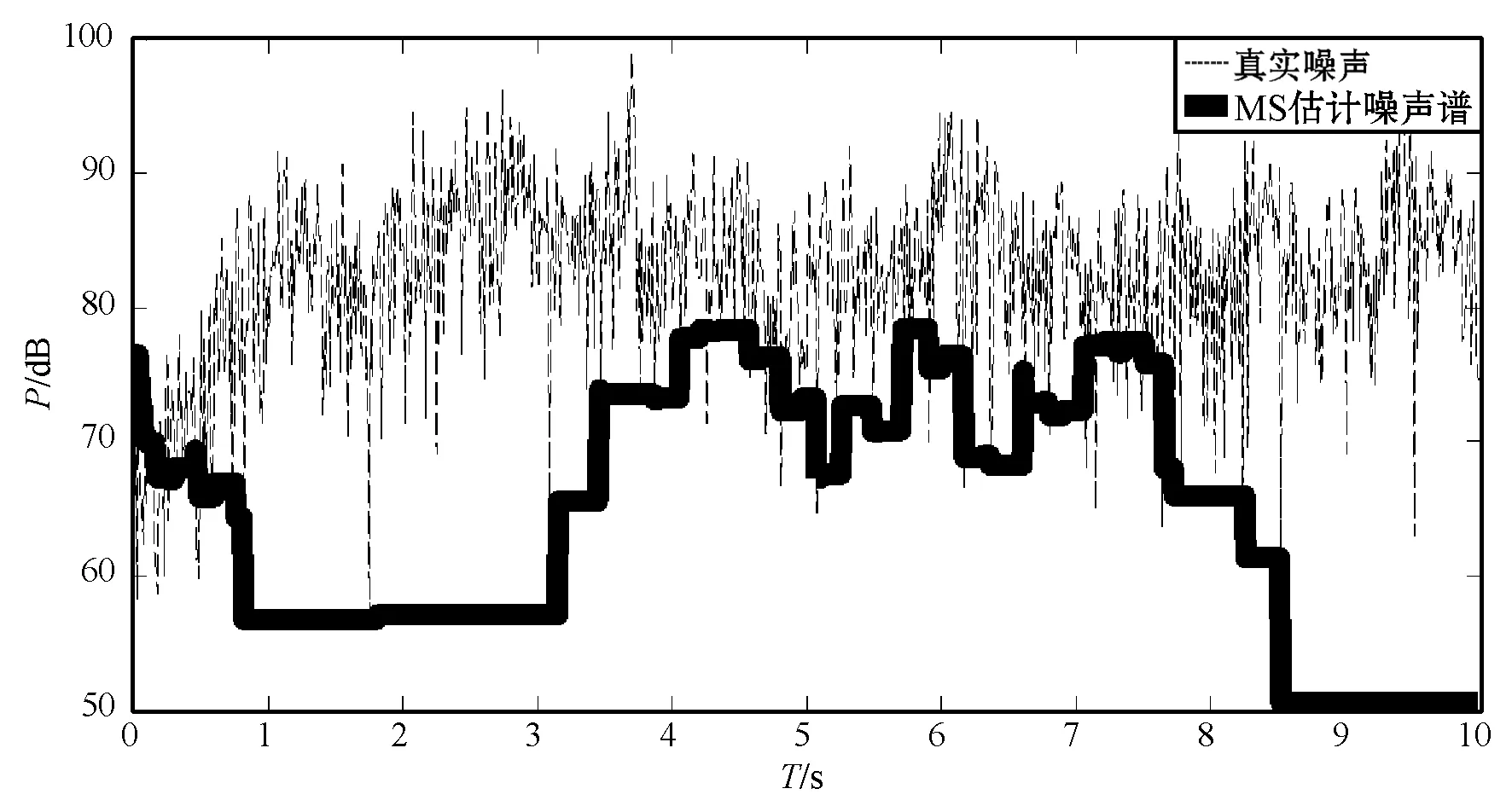
(a) MS估计噪声谱

(b) MCRA估计噪声谱
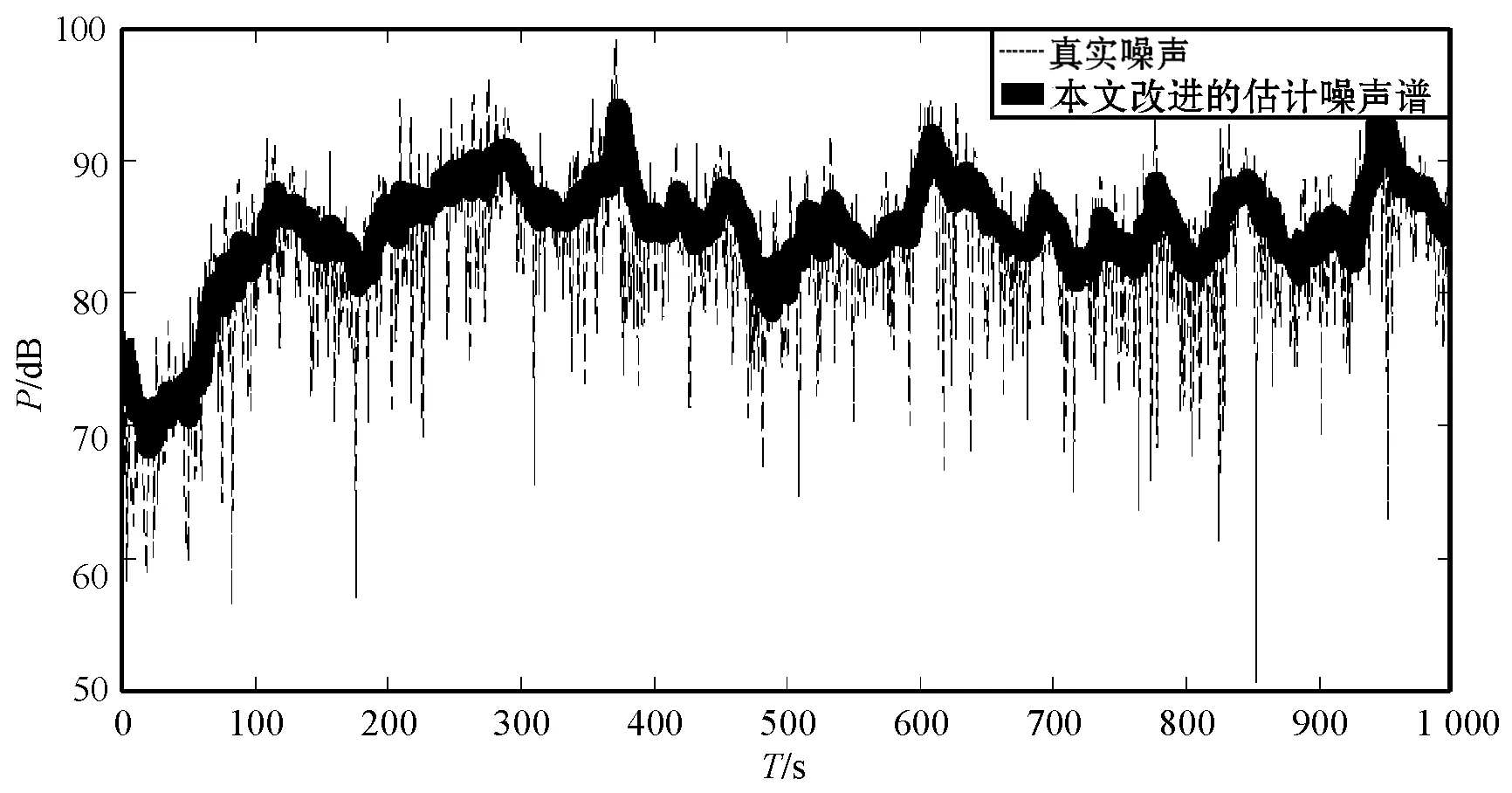
(c) 本文算法估计噪声谱图5 采用三种不同的噪声估计方法得到的 估计噪声谱与真实噪声谱(k=1 700 Hz)
从图5可以看出,本文算法的噪声估计值更接近真实值。MS算法时延较大,本文算法相较于MS算法和MCRA算法在跟踪时延上有较明显改善,尤其是在噪声下降沿。
2.2 改进的谱减法
传统谱减法公式为:
(19)
因传统谱减法产生的“音乐噪声” 会对目标信号产生干扰抑制,所以为降低音乐噪声,将原公式改为:
(20)
式中:α为过减因子(α≥1),ρ(0<ρ≥1)是谱下限参数。参数ρ可以控制残留噪声的多少以及音乐噪声的大小。如果谱下限太大,可能听到残留噪声信号但是感觉不到音乐噪声;相反,如果太小,则可能带来音乐噪声但原噪声信号可以被极大地抑制。因此,对低信噪比ρ取0.002。
α应该随每一帧而变化:
式中:SNR为每一帧的短时信噪比估计,计算是基于带噪信号功率与估计的噪声功率的比率,是信噪比的一种后验估计,表示如下:
图6为去噪前后音频时域波形对比图,我们可以发现,MS算法降噪效果不明显,MCRA算法因存在噪声估计延迟问题并不能有效应用在列车音频降噪中。使用改进算法降噪后的时域信号相比降噪前的时域信号,噪声干扰明显减少,不存在跟踪时延的影响,能有效区分各节车厢的周期。由此可见使用基于改进的最小值控制的递归平均噪声估计算法的改进谱减法对列车行车音频信号进行去噪处理,效果比较理想。
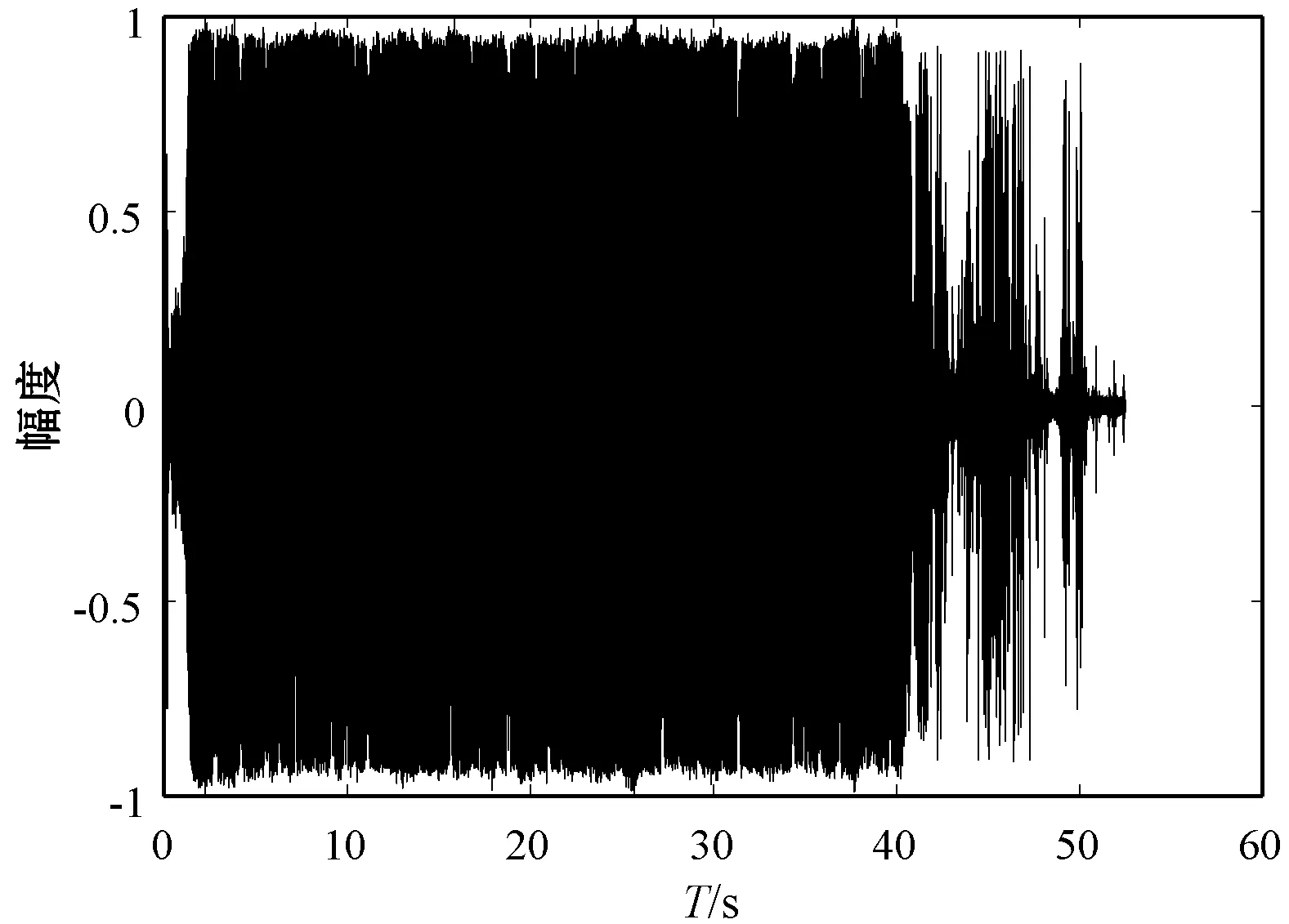
(a) 去噪前音频时域波形
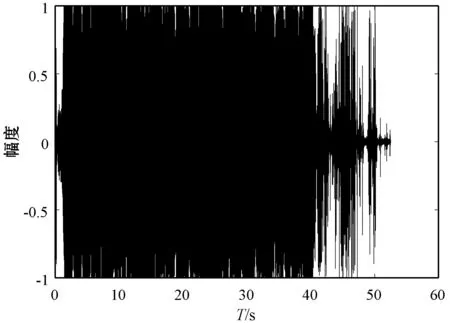
(b) MS算法去噪后时域波形
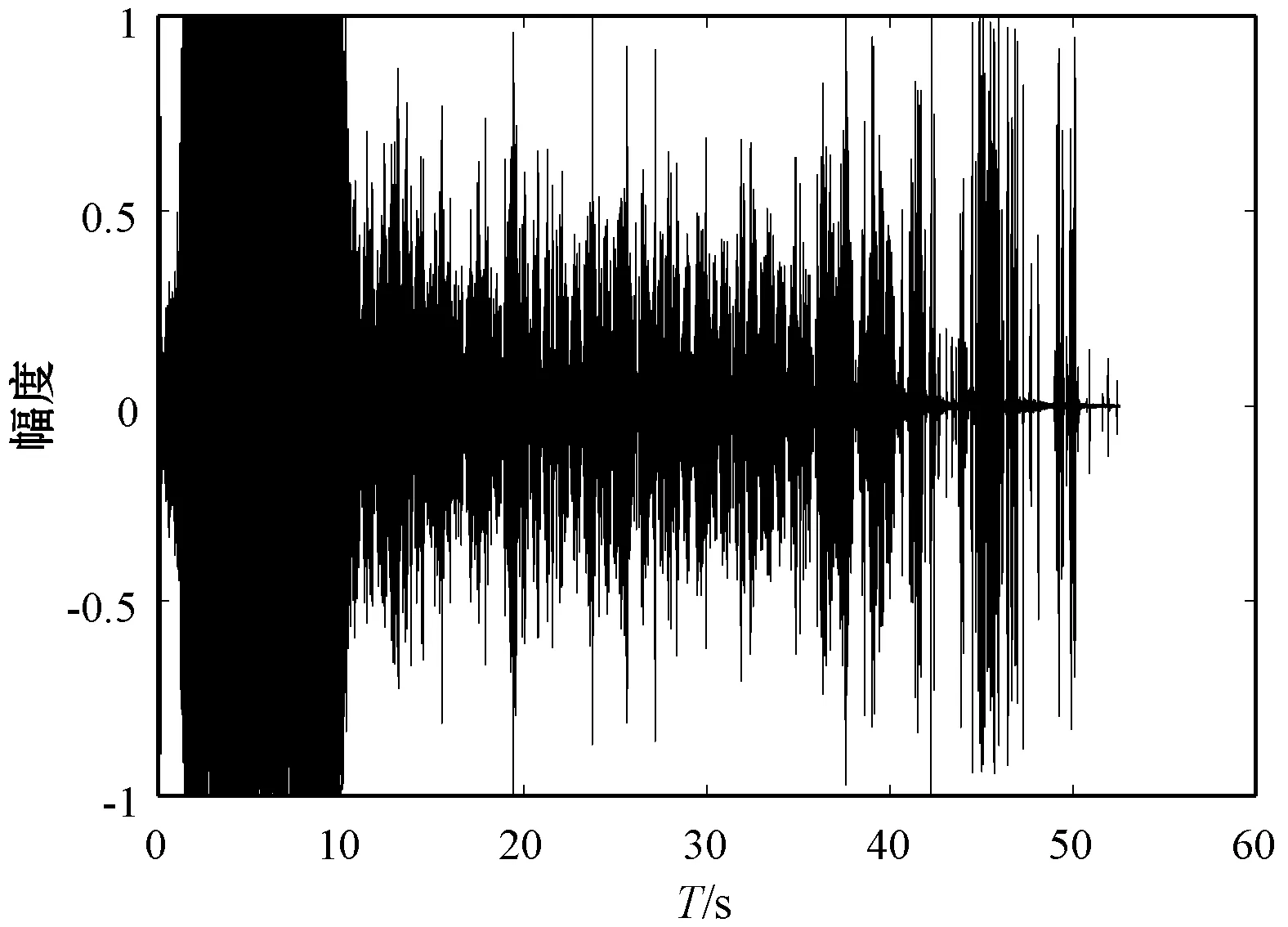
(c) MCRA算法去噪后时域波形
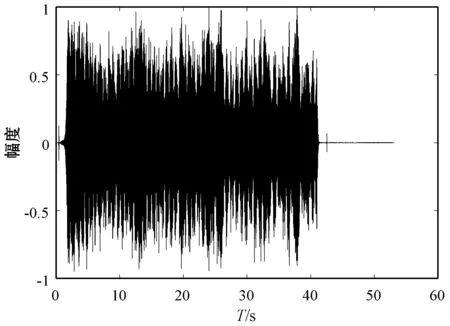
(d) 改进算法去噪后时域波形图6 去噪前后归一化时域波形图
2.3 行车起止时刻及车厢分离方法
2.3.1能熵比端点检测法
对降噪后的行车音频信号采用能熵比端点检测法,确定列车经过声音采集器的具体起止时刻。各频率分量的归一化谱概率密度函数为:
式中:l为对应的频率分量。
每个音频帧的短时谱熵为:

对应的能熵比为:
对于噪声来说,它的归一化谱概率密度函数分布相对均匀,所以它的谱熵值就大。而对于行车音频信号,由于能量变化大,它的归一化谱概率密度函数分布相对不均,行车音频的谱熵低于噪声的谱熵[23]。通过实验确定阈值为0.1,当能熵比值大于阈值时,判定为目标信号存在,利用这一特性确定行车音频起止端点,截取有效音频段。
2.3.2车头车厢分离方法
对有效音频段做希尔伯特变换求时域包络,并计算包络波形中波谷的具体时刻;计算相邻波谷时间差的均值即为列车车厢行驶的平均周期,由于车厢长度已知,即可求出车厢的运行车速;判断有效音频起始时刻到第一个波谷的距离就是车头经过声音采集器所用时间,对其余音频片段按平均周期分割,每一段音频即为一节车厢经过音频采集器所用的时间[24-26]。
2.4 改进的能熵比检测法
2.4.1四类行车异常样本分析
通过分析四类异常行车样本的语谱图,我们发现四类异常能量分布在不同的频段[27-28],选取能量变化较大、集中且频段不重叠的部分,低速抱闸:750~950 Hz、高速抱闸:3 000~3 400 Hz、零件松动:3 800~7 200 Hz、敲击车门:1 850~2 200 Hz,如图7所示。
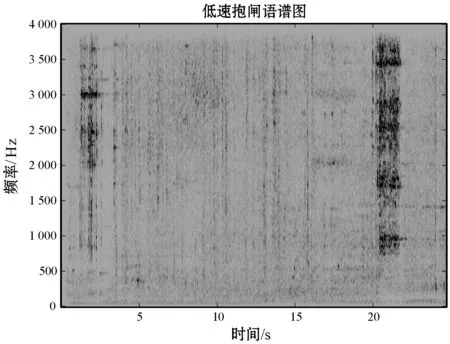
(a) 低速抱闸语谱图
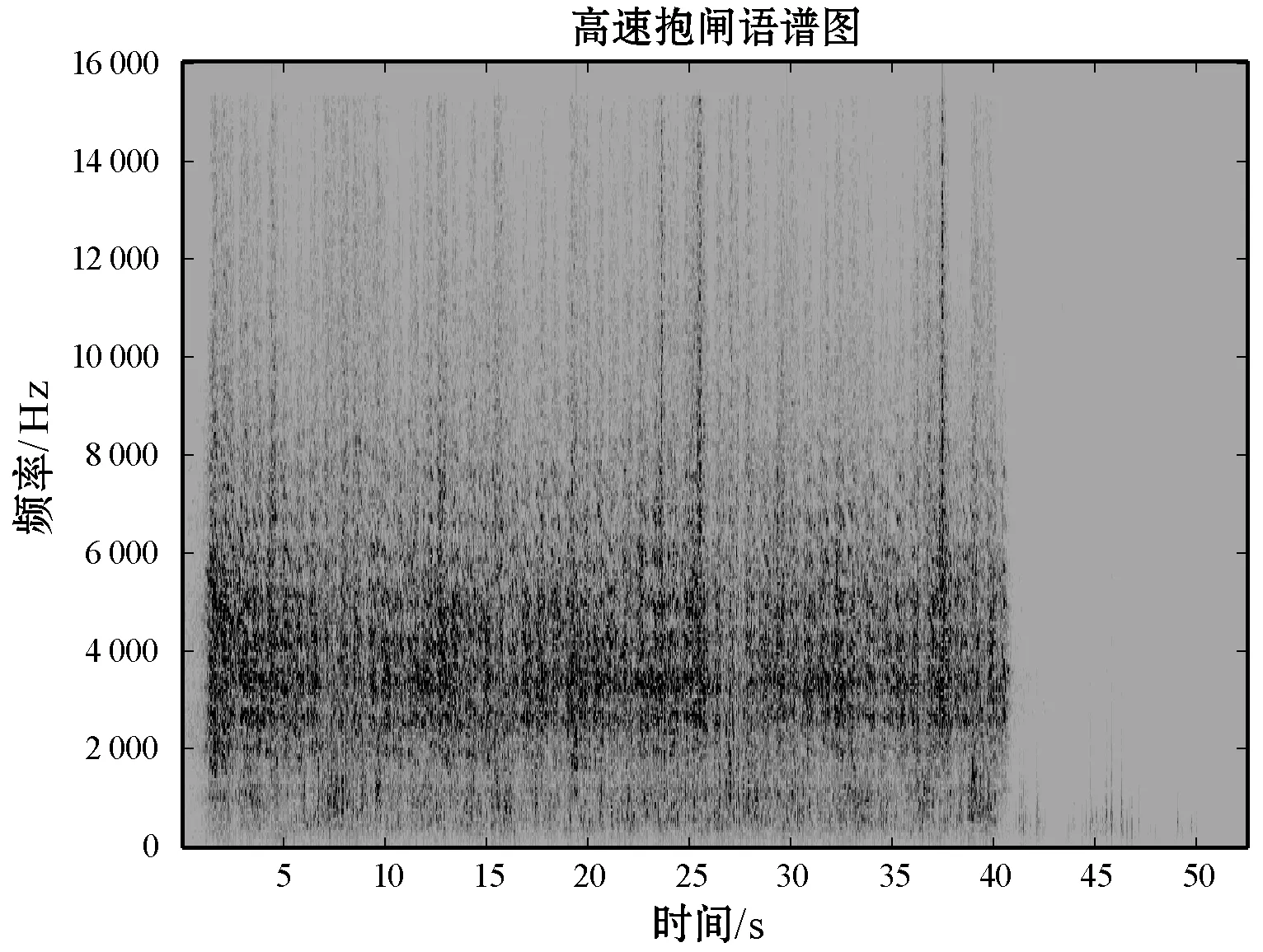
(b) 高速抱闸语谱图
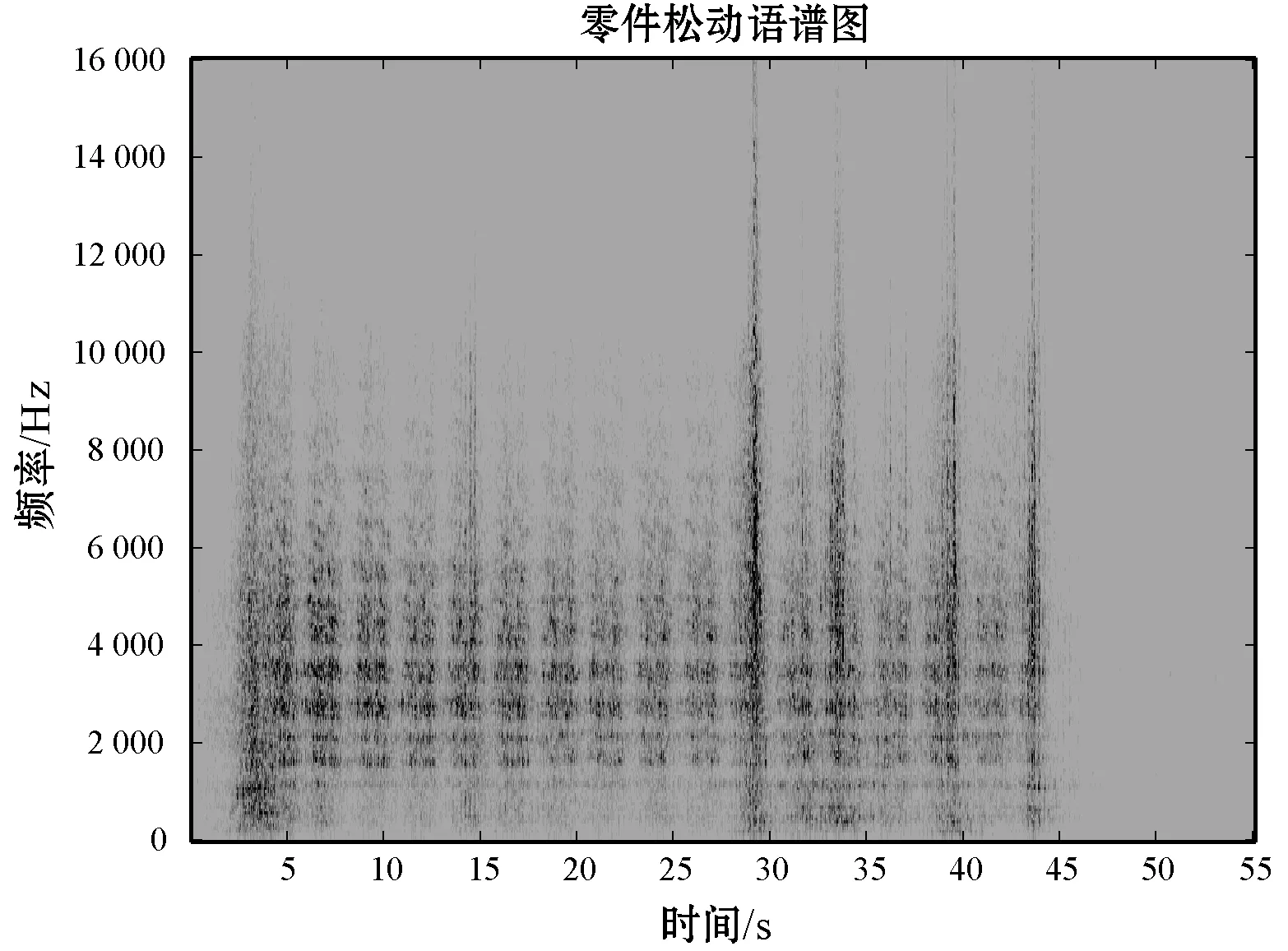
(c) 零件松动语谱图
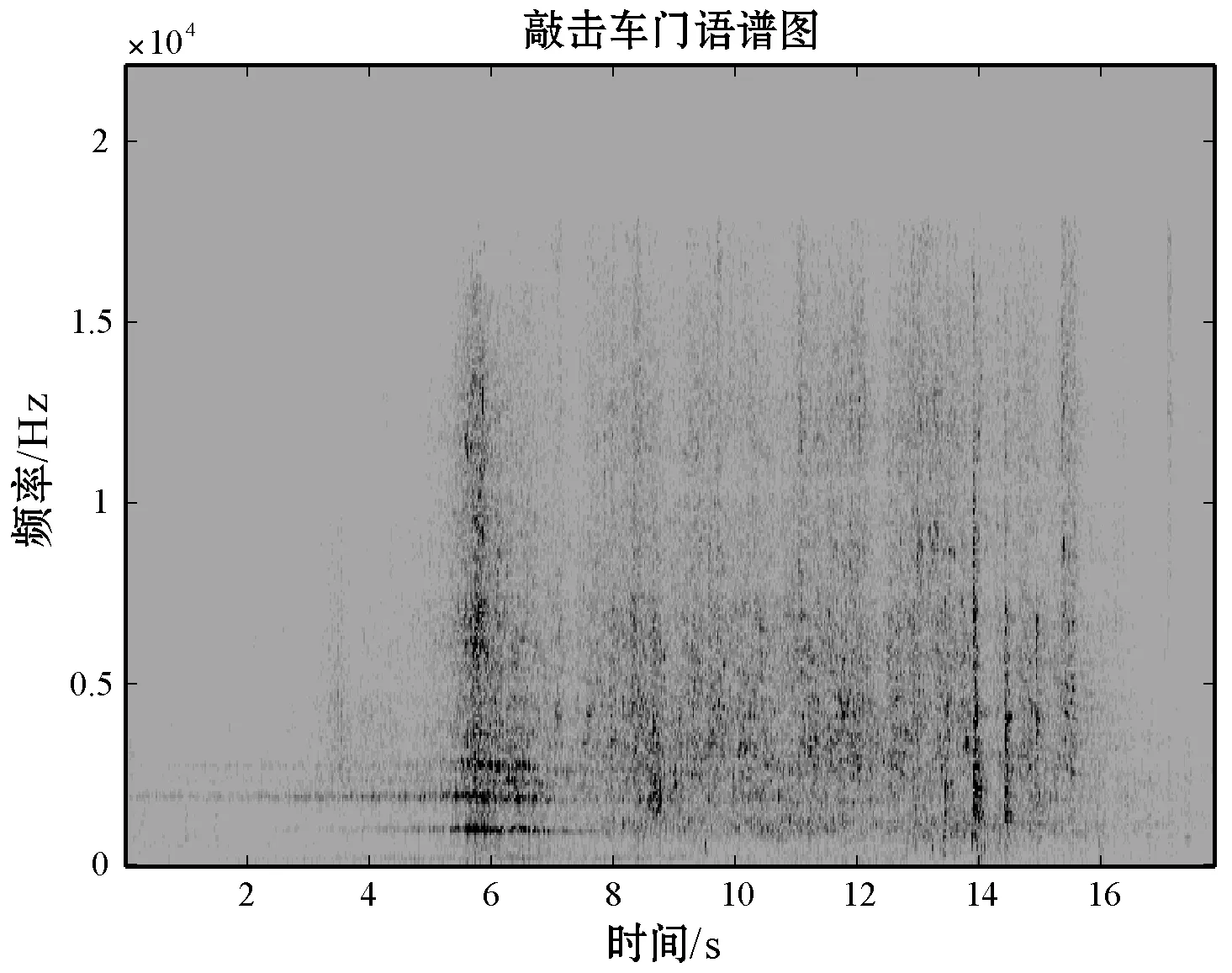
(d) 敲击车门语谱图图7 异常行车样本语谱图
2.4.2改进的能熵比检测法
对应每种异常类型所在频段,分别求异常频段频率分量的归一化谱概率密度函数,同时为降低残留行车噪声对异常识别的影响,引入一个正常量K,得到改进的归一化概率谱密度函数:
式中:K=1;l为四种异常类型对应频段。对比采集到的四类异常样本与正常样本总计5 000段数据,由实验经验总结得到四种异常类型能熵比阈值分别为:低速抱闸0.85、高速抱闸0.85、零件松动0.6、敲击车门0.98,通过对截取的单节车厢音频进行检测判定是否存在异常行驶,并确定异常行驶属于哪一类。四种异常的能熵比检测图如图8所示。
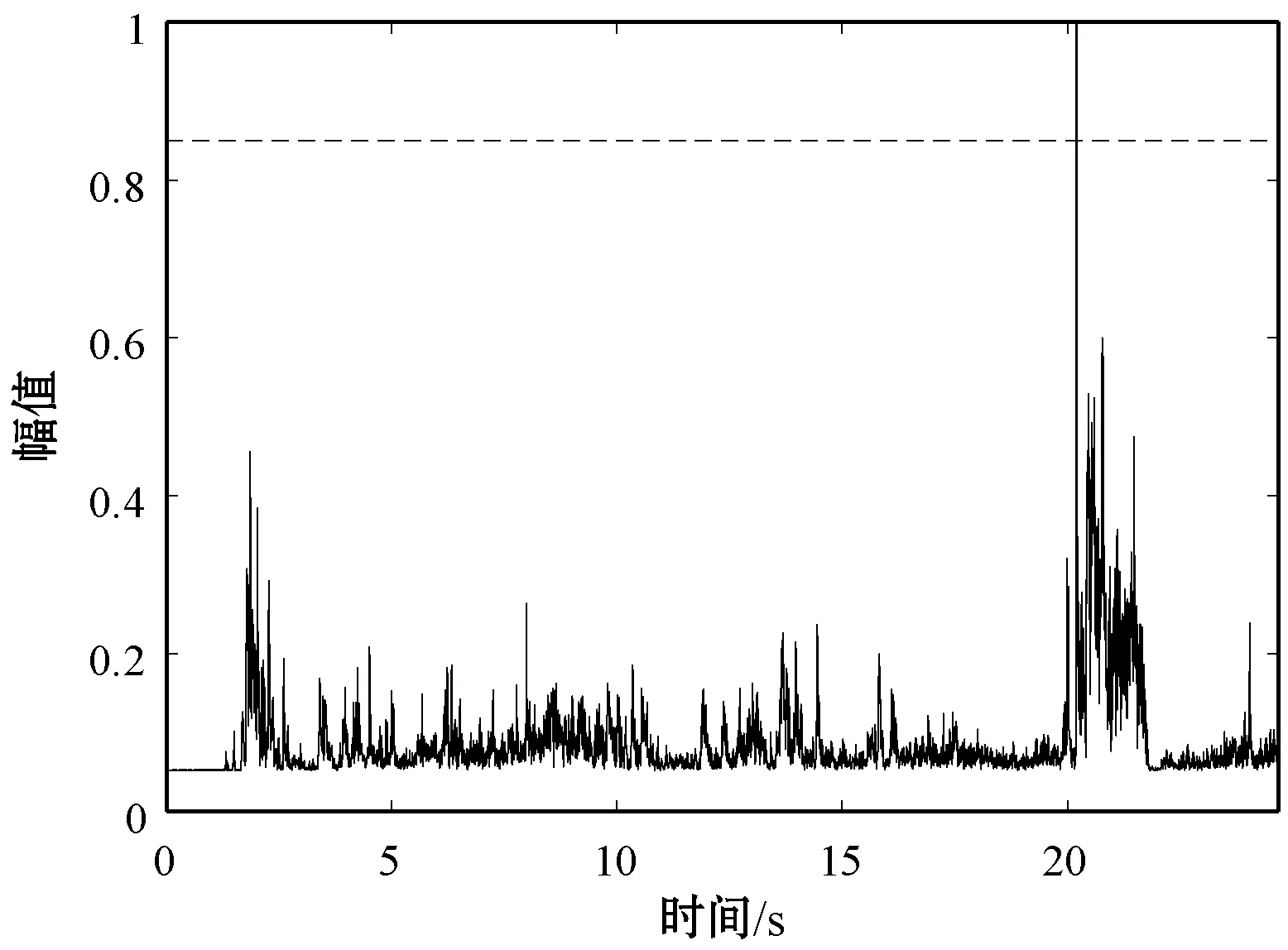
(a) 低速抱闸样本归一化能熵比
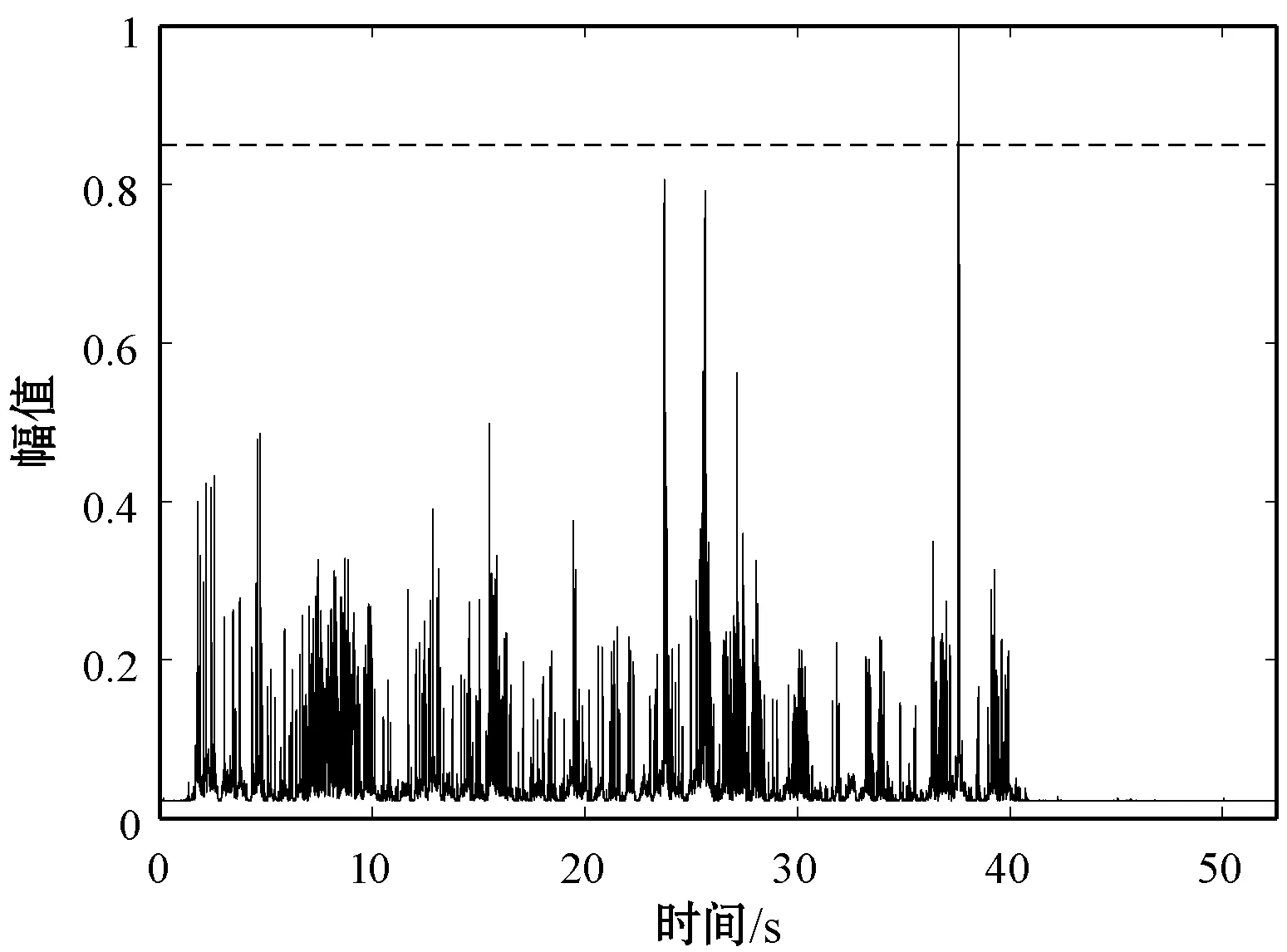
(b) 高速抱闸样本归一化能熵比
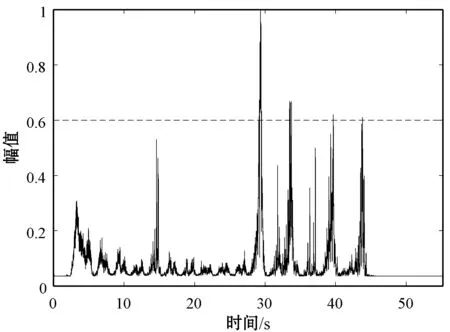
(c) 零件松动样本归一化能熵比
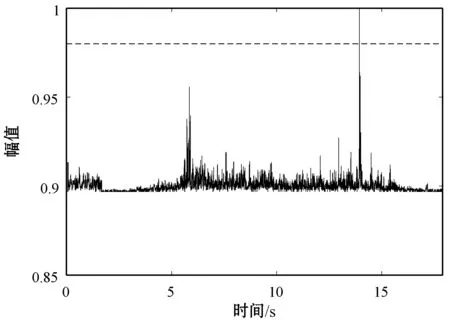
(d) 敲击车门样本归一化能熵比图8 异常行车样本归一化能熵比检测
3 实验验证
3.1 实验样本准备
为了验证本文算法的可行性,在MATLAB环境下对提出的异常检测算法进行仿真实验。异常声音素材主要来自天津静海站、唐官屯站、杨柳青站采集到的行车音频,总共采集了5 000段行车音频,其中正常行车样本4 600段,异常行车样本400段,采样频率为44 100 Hz,保存格式为.aac。因无法采集到纯净行车音频,只能通过最终检测准确率做算法性能分析。
3.2 降噪性能验证实验
在使用改进的能熵比异常检测方法进行检测的基础上,比较本文降噪方法与其他几种降噪方式及不做降噪处理异常检测准确率存在的差异。对比五种情况下,异常行车检测准确率如表1所示。

表1 不同降噪方式下异常检测性能对比 %
分析表1可知:
(1) 不使用降噪处理的情况下,背景环境噪声会对行车音频信号产生严重干扰,直接对信号进行异常检测,无法有效分离车厢、确定异常行车情况所在位置,准确率仅为48%,无法达到应用要求。
(2) 采用本文所述降噪方法时,能够有效定位异常车厢并识别出异常类型,异常行车检测准确率为91%,有一定的实用价值。
(3) 采用其他三种降噪方式时,异常行车检测的准确率较本文所述基于改进MCRA噪声估计的改进谱减法准确率低。所以,采用本文降噪方式能更好地提高异常检测率。
3.3 异常检测性能验证实验
采用改进MCRA噪声估计的改进谱减法做去噪处理,比较本文改进能熵比检测法与传统能熵比检测法以及子带能熵比检测法准确率存在的差异。对比三种情况下,异常行车检测准确率如表2所示。

表2 不同异常检测方式下异常检测性能对比 %
分析表2可知:
(1) 使用传统能熵比检测法,不能有效识别特定异常行车类型,准确率仅为55%,无法达到应用要求。
(2) 采用子带能熵比检测法,虽然通过将一帧分成若干个子带,分别求每个子带的能熵比,进一步降低了残留环境噪声的干扰,但依旧不能有效识别特定异常行车类型,检测准确率为63%。
(3) 采用改进能熵比检测法时,通过引入正常量K,降低了噪声的干扰,又针对异常特征所在频段做改进的能熵比检测,能够有效区分各车厢的异常行车类型,检测准确率为91%。
综上,实验结果表明,采用本文所述异常检测方法时,对异常行车音频具有更好的辨识性能。
4 结 语
利用本文提出的改进MCRA算法进行噪声估计并做改进谱减法的降噪处理,通过实验经验总结优化参数取值,得到较明显的列车行车环境下的消噪效果。
在改进的去噪方法基础上,通过改进的能熵比检测法进行异常类型的判断检测。实验表明,行车异常类型检测辨识准确率达91%。今后将对有效识别不同行车环境的算法进行研究。

