一种改进的K均值算法

李丰兵

摘  要：K均值算法是以随机的方式选择初始聚类中心，这使得K均值算法容易陷入局部最优，收敛性能不稳定。针对这一缺陷，该文对K均值算法进行改进，提出一种逐步选择距离差异极大的个体作为初始聚类中心的算法。实验结果表明，改进后的算法收敛性能确实比K均值算法优越。

关键词：K均值算法  聚类中心  局部最优  收敛性

中图分类号：TP311.13   文献标识码：A             文章编号：1672-3791（2019）05（c）-0185-03

Abstract： K-means algorithm chooses initial clustering centers randomly， which makes K-means algorithm easy to fall into local optimum and its convergence performance unstable. In order to overcome this shortcoming， an improved K-means algorithm has been proposed in this paper， which chooses gradually individuals with great distance difference as the initial clustering center. The experimental results show that the improved algorithm has better convergence performance than K-means algorithm.

Key Words： K-means algorithm; Clustering center; Local optimum; Convergence

K均值算法是21世紀十大机器学习算法之一，是1967年由麦奎因（MacQueen）提出并命名的一种简单、高效的快速聚类算法，广泛地应用于数据挖掘、模式识别及计算机视觉等领域[1-3]。目前，K均值算法仍然是人工智能及机器学习领域的一个研究热点，国内外已存在诸多与K均值算法密切相关的研究工作，其中，有部分研究工作集中在K均值算法的改进问题上[4-8]。众所周知，K均值算法存在两个主要的缺陷，其中一个缺陷就是以随机的方式选择初始聚类中心，而不同的初始聚类中心可能会导致不同的聚类结果，即K均值算法容易陷入局部最优，聚类效果依赖于初始聚类中心的选择，这种情况如图1所示。

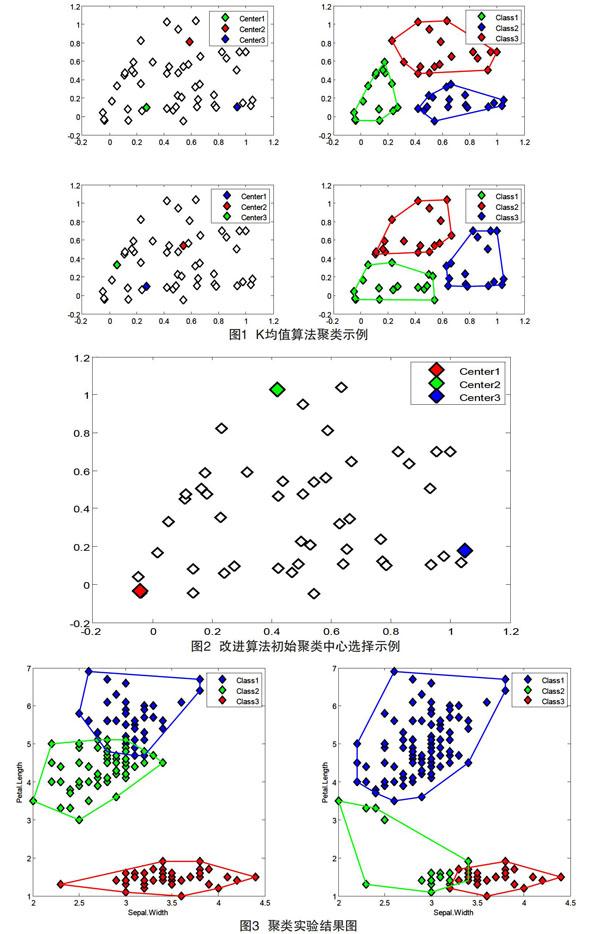
在图1中，左上图和左下图分别表示两种不同的初始聚类中心的选择，这里所用的数据集是相同的，划分类别数均为3，右上图和右下图则分别表示对应的聚类结果。显然，由图1可直观地看出，选择不同初始聚类中心导致K均值算法聚类结果不同。因此，K均值算法是一种局部收敛算法，稳定性及精确性都有待于进一步提高和完善。

1  K均值算法的改进

为改善K均值算法（为避免混淆，以下称经典K均值算法）的上述缺陷，该文提出一种新的初始聚类中心的选择算法。该算法的思想是以类与类之间存在较大差异为根据，通过迭代搜索逐步确定具有较大距离间隔的初始聚类中心，具体步骤如下。

步4：确定集合C中所有个体与重心的最小距离dmin=min{di|i∈IC}及集合中所有个体与重心的最大距离dmax=min{di|i∈I}。

步5：若dmax-dmin<δ中，则算法停止迭代，集合C中的个体即为K均值算法的初始聚类中心，否则将集合C中个体Xmin与集合中个体Xmax互换，并转第3步。

以图1中的数据集为例，利用该改进方法，可求得初始聚类中心，如图2所示。

从图2中可直观看出，改进算法确定3个初始聚类中心从位置分布上看非常分散。以这种极度分散的初始聚类中心进行聚类，可以减缓K均值算法陷入局部最优的可能，下面的实验仿真可以说明这一问题。

2  实验仿真

为了验证改进的K均值算法的有效性，下面采用UCI数据库中的标准数据Iris对经典K均值算法和改进的K均值算法进行对比实验。Iris数据也称为鸢尾花卉数据，是Fisher于1936收集整理的，常用来作为模式分类实验数据集。Iris数据集共包含3类鸢尾花卉数据（Setosa，Versicolour，Virginica），每一类均包含50个样本个体数据，每个个体数据又包含4个属性，分别为：Sepal.Length、Sepal.Width、Petal.Length及Petal.Width。实验方法如下，取划分类别数k=3，计算精度值δ=0.01，分别对经典K均值算法和改进的K均值算法进行50次实验，记录每次实验的分类结果及错分个体数。

实验结果如下，经典K均值算法共出现两种聚类结果，其中有37次实验结果如图3的左图所示，其余13次实验结果如图3的右图所示，而改进的K均值算法只有图3的左图一种结果（这里为了演示方便、简洁，只画出鸢尾花卉数据的两种属性平面图）。由此可知，改进的K均值算法比经典K均值算法稳定性要好。另外，从聚类精度来看，改进的K均值算法每次错分样本个体数均为18，而经典K均值算法有37次实验中错分个体数为18，其余13次错分个体数达到92，总共150个个体数据，换算成错分率后结果如图4所示。

从图4中可直观看出，改进的K均值算法错分率稳定在10%附近，而经典K均值算法竟然有13次错分率超过50%，由此可知，改进的K均值算法比经典K均值算法聚类结果更加准确。

3  结语

该文针对经典K均值算法随机选择初始聚类中心的缺陷进行改进，提出一种利用逐步迭代的方式选择距离差异极大的个体作为初始聚类中心的算法。利用UCI数据库中的标准数据Iris进行50次对比实验，结果表明改进的K均值算法不但稳定性比经典K均值算法要好，而且聚类精度也比经典K均值算法要高。尽管如此，改进的K均值算法仍需做进一步研究，算法的收敛性能有待于进一步提高。

参考文献

[1] Mourade Azrour， Yousef Farhaoui， Mohammed Ouanan， et al.SPIT Detection in Telephony over IP Using K-Means Algorithm[J].Procedia Computer Science， 2019（148）：542-551.

[2] Tanvir Habib Sardar， Zahid Ansari.An analysis of MapReduce efficiency in document clustering using parallel K-means algorithm[J].Future Computing and Informatics Journal，2018，3（2）：200-209.

[3] Kisoo Kwon， Jong Won Shin， Nam Soo Kim. Incremental basis estimation adopting global k-means algorithm for NMF-based noise reduction[J].Applied Acoustics， 2018（129）：277-283.

[4] 贾瑞玉，李玉功.类簇数目和初始中心点自确定的K-means算法[J].计算机工程与应用，2018，54（7）：152-158.

[5] Shyr Shen Yu， Shao Wei Chu， Chuin Mu Wang， et al.Two improved k-means algorithms[J].Applied Soft Computing，2018（68）：747-755.

[6] Geng Zhang，Chengchang Zhang， Huayu Zhang.Improved K-means algorithm based on density Canopy[J].Knowledge-Based Systems，2018（145）：289-297.

[7] 谢娟英，王艳娥.最小方差优化初始聚类中心的K-means算法[J].计算机工程，2014，40（8）：205-211，223.

[8] 邢長征，谷浩.基于平均密度优化初始聚类中心的k-means算法[J].计算机工程与应用，2014，50（20）：135-138.