芦苇秆热解特性及动力学分析

张 旭, 孙 姣, 范 赢, 曹永全, 陈文义*

(1.河北工业大学 过程装备与控制工程系， 天津 300130； 2.河北工业大学 工程流动与过程强化研究中心， 天津 300130)

随着经济持续发展，不可再生化石燃料需求量不断增加，储备量持续下降，且其燃烧也对环境造成严重污染，因此可再生和可持续能源的开发成为研究者们关注的焦点[1-3]。生物质能源因具有清洁、可再生和可持续的特点，成为化石燃料的潜在替代品[4-5]。芦苇作为生物质原料，资源丰富，仅中国范围内就有14个主产区，面积达到130万hm2以上，大量无法合理利用的芦苇被废弃或焚烧，造成资源浪费和环境污染。因此充分利用芦苇生物质能源可减轻能源压力并缓解环境污染[6-7]。目前，在生物质能源化利用中生物质热解技术较为常见，通过热解可获得气体、液体、固体3种产品[8]。为更好了解生物质热解过程，对热解特性及热解动力学的研究显得尤为重要。在芦苇秆热解特性研究中，Sutcu[9]分析了芦苇热解固体与液体产物的特性；Barbooti[10]通过热解实验发现芦苇可作为潜在生物质能源候选资源，其热解气体与挥发性物质极具利用价值。热解反应动力学参数通常通过热重分析确定，目前热重分析中非等温法应用广泛[11]，其中包括多种计算方法，例如较为经典的Coats-Redfern法，Flynn-Wall-Ozawa法、Kissinger-Akahira-Sunose法以及分布活化能法等[12-13]。在芦苇热解动力学研究中，Zhao等[14]利用Doyle和Coats-Redfern 2种不同近似积分方法对热解过程进行动力学参数计算。而不同计算方法得到的动力学参数也不同，因此比较不同方法计算的结果，确定合理的动力学模型及参数对芦苇热解特性研究和生物质能的发展利用具有重要的理论意义与实际应用价值。区别于其他芦苇热解的研究，本研究以3种不同加热速率(10、 20、 30 ℃/min)对芦苇秆进行热重实验，并采用Coats-Redfern法、Flynn-Wall-Ozawa法、Kissinger-Akahira-Sunose法对数据进行分析，得到更精确的动力学参数，包括活化能(E)、指前因子(A)和反应级数(n)，以确定适合芦苇秆热解的动力学方法，详细分析了芦苇秆热解特性，以期为芦苇生物质的合理利用提供理论基础。

1 材料与方法

1.1 材料

实验采用来自吉林松原的芦苇秆，在60 ℃下干燥12 h除去水分，然后粉碎并筛分出0.18～0.25 mm的原料，备用。对芦苇秆原料进行工业分析、元素分析和组分分析。工业分析采用干燥无灰基样品进行测试，结果为水分5.46%、灰分12.05%、挥发分70.70%、固定碳13.79%；元素分析结果为C 45.62%、H 5.23%、O 47.90%、N 1.12%、S 0.13%(其中O元素的量通过差减法得到)；组分分析结果为半纤维素24.64%、木质素23.83%、纤维素45.61%。

1.2 热解实验

使用美国TA公司的SDT/Q600同步热分析仪对芦苇秆进行非等温热解实验。取5～6 mg已粉碎的芦苇秆，放入Al2O3坩埚中，在氮气流量为100 mL/min的条件下，分别以10、 20、 30 ℃/min的升温速率由30 ℃升温至900 ℃。

1.3 热解动力学

生物质热解的一般途径可以概括为生物质→炭+挥发物+气体[9]。生物质原料在程序升温下发生分解反应，其反应的动力学可以表示为：

(1)

式中：α—转化率，α= (m0-mt)/(m0-m∞)；m0和m∞—生物质原料反应的起始质量、最终剩余质量，kg；mt—反应至t时刻样品的质量，kg；k—速率常数，k=Aexp(-E/RT)；E—反应活化能，kJ/mol;A—指前因子,min-1；R—气体常量，8.314 J/(mol·K)。

f(α)的函数形式取决于反应类型或反应机制，可假设f(α)与温度(T)和时间(t)无关，只与α有关。因此式(1)可以表达为：

(2)

其中，升温速率见式(3)：

(3)

将式(3)代入式(2)中可得：

(4)

对式(4)进行积分可得式(5)：

(5)

这里x=E/RT,函数P(x)没有精确的解。因此，式(5)可以通过数值方法或近似来求解。

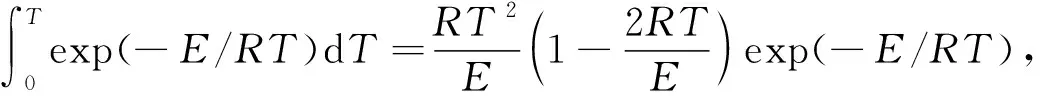
当n≠1时，

(6)

当n=1时，

(7)

式中对于一般的反应温区和大部分的E值而言，E/RT远大于1，所以(1-2RT/E)≈1，因此ln[(AR/βE)(1-2RT/E)]≈ln(AR/βE)，可以看作常数；此外，式中n表示反应级数，当n≠1时，ln[(1-(1-α)1-n/T2(1-n)]对1/T作图，当n=1时，ln[-ln(1-α)/T2]对1/T作图，得到一条直线，根据斜率和截距分别求得活化能(E)和指前因子(A),得到动力学参数后，转化率(α)可以根据式(7)得到：

(8)

1.3.2 Flynn-Wall-Ozawa法 Flynn-Wall-Ozawa(FWO)法[16]是一种无函数模型法的积分法，避开了反应机理函数的选择而直接求解活化能，因此不会因为反应机理函数的假设不同而带来误差。在FWO法中使用的Doyle的近似式[17]为：

P(x)=0.004 84exp(-1.051 6x)

(9)

联立式(5)与式(9)可得到FWO法方程式为：

(10)

在FWO法中选择不同β，相同的α，得到lgβ和 1/T的线性关系图,再根据拟合直线的斜率得到活化能(E)值。采用主函数图法[18]对机理函数进行筛选，由式(5)可知，对于合理的机理函数可以得到：

(11)

式中G(0.5)、P(x0.5)表示在α=0.5时对应的G(α)和P(x)。可以根据理论值G(α)/G(0.5)与实验值的P(x)/P(x0.5)对比，选择合适的反应机理函数以及确定合适的动力学模型。

1.3.3 Kissinger-Akahira-Sunose方法 Kissinger-Akahira-Sunose(KAS)法[19]也是一种无函数模型法，其采用的经验近似式是：

P(x)=x-2exp(-x)

(12)

将近似值应用于式(5)后，表达式为：

(13)

在ln(β/T2)对1/T的曲线图中，斜率为-E/R，其中R为8.314 J/(mol·K)。通过在0到1的转换范围内的计算，可计算对应于转化率的活化能(E)。

2 结果与讨论

2.1 芦苇秆热解特性分析

图1(a)和(b)分别为芦苇秆在不同升温速率下的热重及热失重速率曲线图。随着升温速率的升高，TG曲线呈现出向右偏移的现象，说明升温速率越高，达到相同质量损失时所需时间越长，这可能是因为升温速率变高，生物质来不及热解完全，当达到相同质量损失时，所需时间较长。DTG曲线随着升温速率的升高也呈现出右移现象，说明随着升温速率的升高，其热失重速率变化剧烈，可能是因为升温速率变高，热解时分子反应剧烈造成的。根据图中曲线变化规律可知在3个升温速率下芦苇秆热解均可分为4个阶段。第一阶段为干燥阶段，此阶段温度小于105 ℃，由于芦苇秆原料失去自由水，因此TG曲线出现了5%左右的质量损失，DTG曲线也相应的有一个较小的波动。第二阶段为105～190 ℃，此阶段质量基本不变，只有少量的生物质发生解聚及玻璃化转变[20]。第三阶段为质量快速减少阶段，温度为190～400 ℃，是芦苇秆主要的热解阶段，该阶段失重率达到65%左右，TG曲线急剧下降，DTG曲线出现了2个比较明显的峰值。芦苇秆是由纤维素、半纤维素和木质素组成的生物质，并且每个组分具有不同的分解温度[21]。根据DTG曲线图可以看出，第一个峰值出现在300 ℃左右，而半纤维素的热解区间为225～325 ℃[22-23]，所以推断第一个峰的形成可能是因为芦苇秆中含量相对较多的半纤维素热解产生的。在DTG曲线中，第二个峰出现的温度在370 ℃左右且峰值较高，因为芦苇秆中含量最多的纤维素热解温度范围为325～375 ℃[22-24]，所以推断第二个峰的形成原因是纤维素热解并且生成大量不可冷凝性气体和可冷凝性挥发分。第四阶段为炭化阶段，此阶段主要是剩余的木质素热解以及残留在木炭中的挥发分析出，木质素热解温度范围比较广，热解温度为160～900 ℃，在温度达到400 ℃以上时，木质素部分发生芳构化热解过程[25-26]且在460 ℃下焦炭产率达到最大[13]，因芦苇秆中木质素含量相对较低，所以此阶段的失重率仅为25%左右。

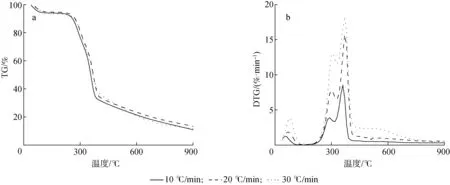
图1 不同升温速率下芦苇秆热解的TG(a)和DTG(b)曲线Fig.1 TG(a) and DTG(b) curves for pyrolysis of Phragmites australis stalk at different heating rates

为了更好地了解热解速率对芦苇秆热解特性的影响，从TG-DTG曲线中获得了主要热解阶段(第三阶段)的几个特征参数并列于表1中。

如表1所示，随着升温速率从10 ℃/min提高到30 ℃/min，第三阶段的热解初始温度和最终温度有向高温侧移动的趋势，并且最大失重速率所对应的温度也有增大的趋势，与Kim等[4]的观点是吻合的。这是由于在较高升温速率下，从颗粒外部到内部的传热需要更长的时间[27]，降低了传热效率，所以到达最大失重速率时的温度升高。另外，失重率没有明显变化，说明升温速率的变化对失重率无明显影响。

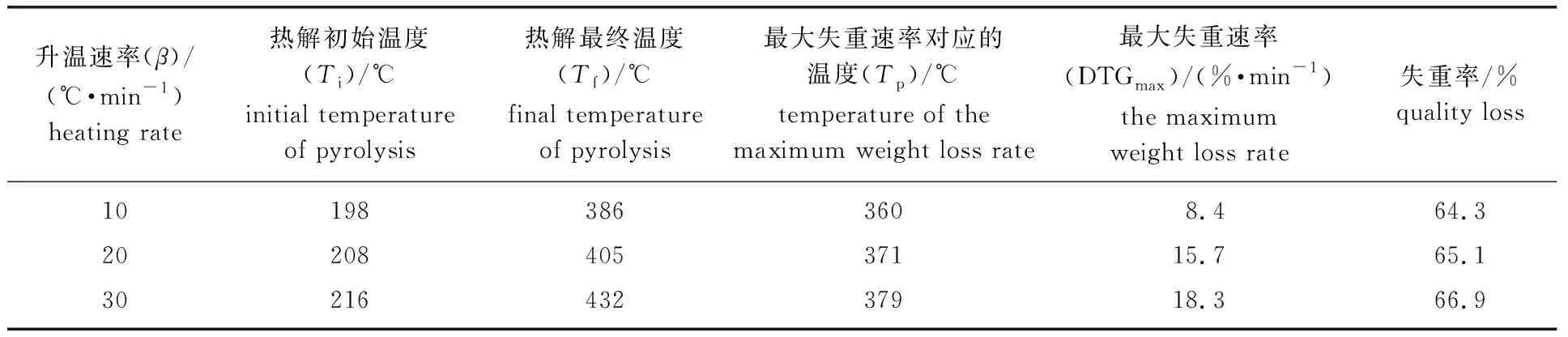
表1 芦苇秆第三阶段热解过程的主要特征参数

2.2 芦苇秆热解的动力学分析

2.2.1 Coats-Redfern法动力学分析 TG曲线表明芦苇秆热解时，65%左右的质量损失发生在190 ℃到400 ℃区间，该温度段为主要热解阶段。假定反应级数n=1，将通过CR法计算得到的不同升温速率下此阶段的动力学参数列于表2中。可以看出，此阶段平均活化能为82.8 kJ/mol，随着升温速率的提高，反应活化能和指前因子也相应提高。

表2 CR法计算的热解第三阶段的动力学参数

图2分别表示10、 20、 30 ℃/min 3种升温速率下芦苇秆热解主要阶段转化率的实验值与CR法计算值的比较。从图2看出，CR法计算的芦苇秆主要热解阶段的转化率结果与实验值在较低温度(200～250 ℃)时较吻合，但随着温度和反应速率的提高，计算结果与实验结果出现较大的偏差。这说明CR法适用于低温热解阶段，也说明芦苇秆快速热解阶段并不是由单一热解反应组成的。

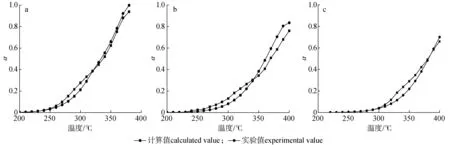
a. 10 ℃/min; b. 20 ℃/min; c. 30 ℃/min图2 不同升温速率下转化率的实验值和CR法计算值的比较图Fig.2 Experimental and calculated curves by CR method at different heating rates

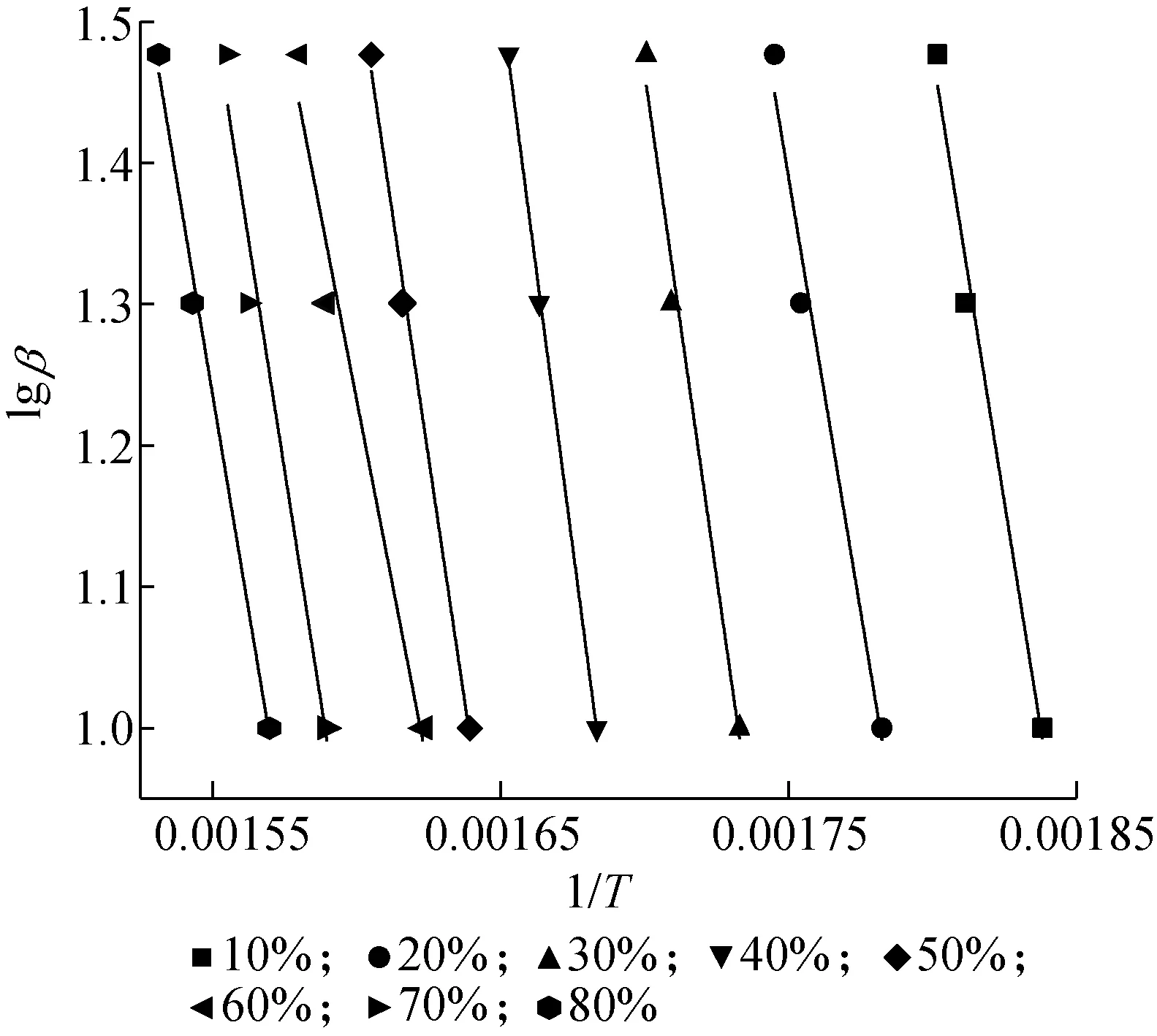
图3 FWO法线性图 Fig.3 Liner plots for FWO method

2.2.2 Flynn-Wall-Ozawa法动力学分析 采用无函数模型法中的FWO法计算芦苇秆热解的动力学参数。根据TG曲线可以看出，芦苇秆热解转化率在0～10%时，转化速率较慢，而其快速热解阶段的转化率为10%～80%，所以研究了转化率10%～80%内活化能的变化情况。根据FWO法，活化能可根据式(10)中lgβ对1/T的线性关系确定。图3给出了不同转化率下的lgβ对1/T的线性关系,并将计算的动力学参数列于表3中。从图3和表3可以看出，FWO法计算的不同转化率下的动力学参数的相关系数大于0.95，说明FWO法能够较好地描述芦苇秆热解过程，而由于热解过程是一个复杂的过程，所以活化能在不同转化率下存在一定范围的波动，波动范围为从221.8 kJ/mol到286.2 kJ/mol。

从表3中还可以看出热解的活化能(E)和指前因子(A)2个动力学参数均呈现出先增大后减小的趋势，活化能在转化率为50%的时候达到最大值，且整个过程中活化能变化较明显，说明该过程必须被估计为多步动力学[27]。这也是CR法计算芦苇秆热解动力学参数选择一级反应模型时计算值与实验值有较大差别的原因。计算可知，指前因子(A)从5.06×108min-1变到5.42×1016min-1，变化了8个数量级，呈现出了较大的波动，并且与活化能表现出良好的线性关系，其表达式为lnA=0.186E-15.15，表明活化能(E)与lnA满足动力学补偿效应[5]。

表3 FWO 法计算的动力学参数

表4中展示了常见的固相反应机理函数[28],以及G(α)/G(0.5)和P(x)/P(x0.5)之间的残差平方和，其值越小，表明反应机理函数越适合反应过程。残差平方和表达式为：

(14)

通过表4可以看出,在FWO法中反应机理函数为随机成核A2，反应级数为n=2时，δ2值最小，转化率的计算结果与实验结果最为吻合。将A2模型代入到式(11)中，可得到转化率的计算式：

(15)

表4 常见的固相反应机理函数

续表4

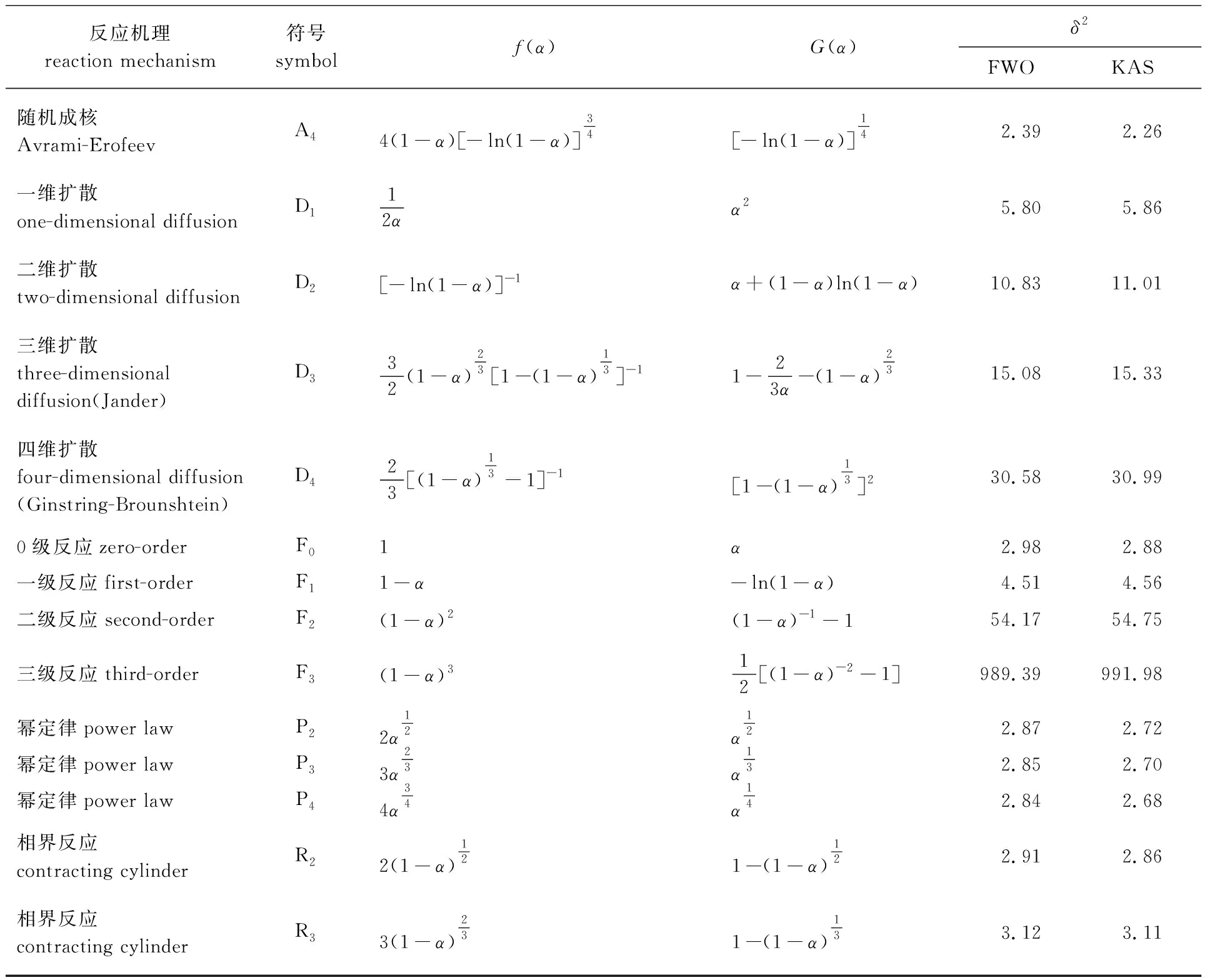
反应机理reaction mechanism 符号symbolf(α)G(α)δ2FWOKAS随机成核Avrami-ErofeevA44(1-α)[-ln(1-α)]34[-ln(1-α)]14 2.39 2.26一维扩散one-dimensional diffusionD112αα25.805.86二维扩散two-dimensional diffusionD2[-ln(1-α)]-1α+(1-α)ln(1-α)10.8311.01三维扩散three-dimensional diffusion(Jander)D332(1-α)23[1-(1-α)13]-11-23α-(1-α)2315.0815.33四维扩散four-dimensional diffusion(Ginstring-Brounshtein)D423[(1-α)13-1]-1[1-(1-α)13]230.5830.990级反应zero-orderF01α2.982.88一级反应first-orderF11-α-ln(1-α)4.514.56二级反应second-orderF2(1-α)2(1-α)-1-154.1754.75三级反应third-orderF3(1-α)312[(1-α)-2-1]989.39991.98幂定律power lawP22α12α122.872.72幂定律power lawP33α23α132.852.70幂定律power lawP44α34α142.842.68相界反应contracting cylinderR22(1-α)121-(1-α)122.912.86相界反应contracting cylinderR33(1-α)231-(1-α)133.123.11

图4为不同升温速率下FWO法计算的转化率值与实验值的对比图。从图4可以发现计算值与实验值有较好的一致性，但是随着转化率的变化仍然有一些差异，说明计算值并不能完全还原实验过程。

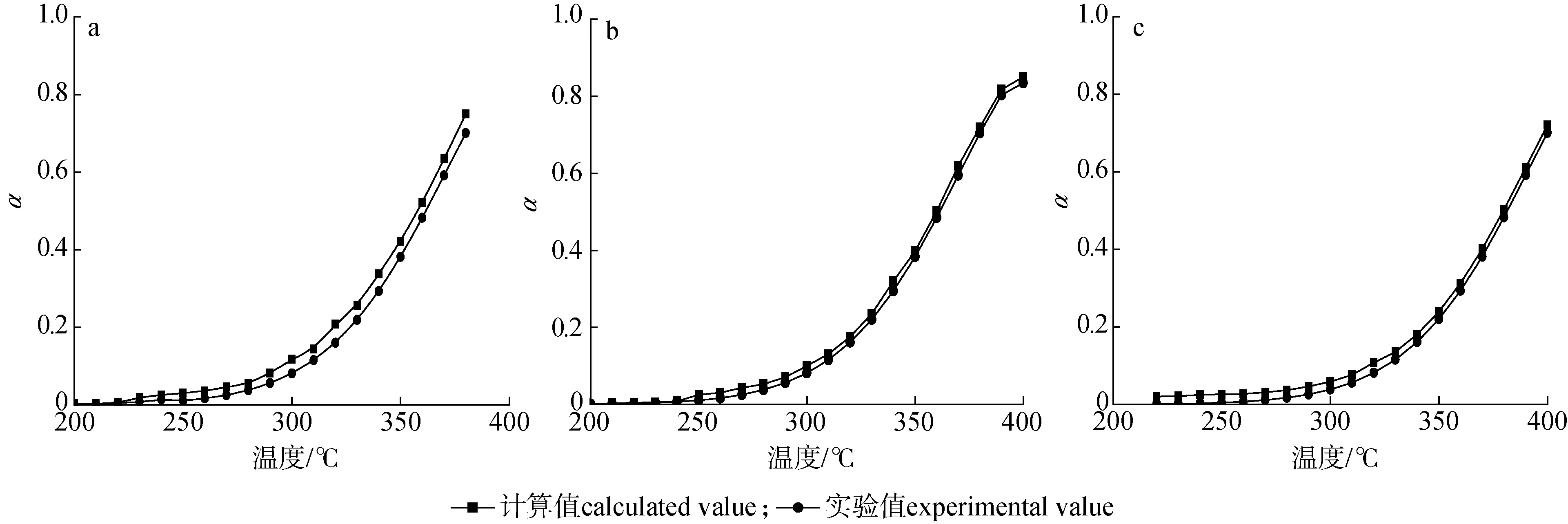
a. 10 ℃/min; b. 20 ℃/min; c. 30 ℃/min图4 不同升温速率下FWO法计算的转化率值与实验值对比图Fig.4 Experimental and calculated curves by FWO method at different heating rates

FWO法相比于CR法更适用于芦苇秆热解，可以更好地描述芦苇秆热解的全过程，但根据图4可以看出，实验值与计算值仍存在一些差距。

图5 KAS法线性图 Fig.5 Liner plots for KAS method

2.2.3 Kissinger-Akahira-Sunose法动力学分析 通过KAS法得到的不同转化率下的ln(β/T2)和1/T的线性关系图见图5，活化能和指前因子列于表5中，可以看出KAS计算的活化能与FWO计算的活化能相差不大，且线性相关性也较高，计算得到活化能(E)随转化率(α)的变化范围是220.1～286.9 kJ/mol,A从5.60×109min-1变化到5.38×1015min-1。活化能(E)和lnA之间的动力学补偿效应线性关系式为lnA=0.196E-17.85，说明活化能与指前因子之间存在着相互补偿的关系。

根据表4可知，同FWO法一样，反应机理函数A2的δ2最小，故A2同样适用于KAS法计算芦苇秆热解的动力学参数。因此可以得出KAS法转化率(α)的计算式：

(16)

表5 KAS 法计算的动力学参数

图6给出了不同升温速率下转化率(α)的实验值与KAS法计算值的比较，当转化率为10%～80%时，其计算结果与实验数据吻合度较高，说明KAS法能够较好地描述此转化率段的热解反应。

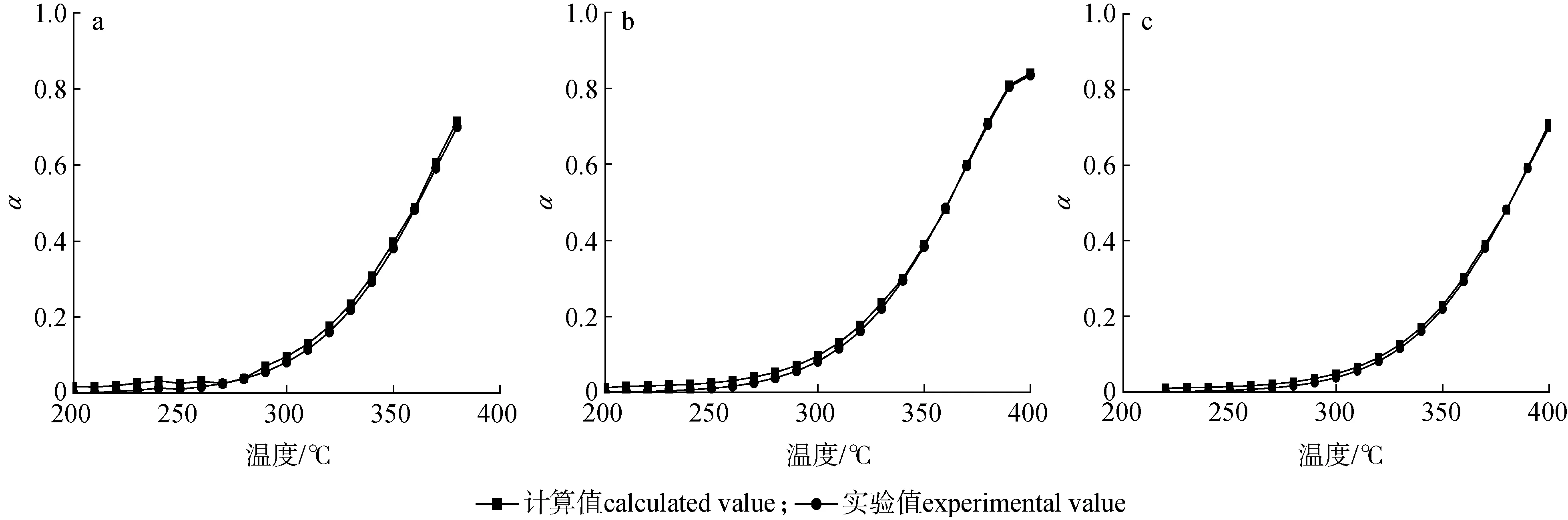
a. 10 ℃/min; b. 20 ℃/min; c. 30 ℃/min图6 不同升温速率下转化率的实验值和KAS法的计算值的比较图Fig.6 Experimental and calculated curves by KAS method at different heating rates

由于芦苇秆中各组分的化学性质不同，其热解十分复杂，单一的动力学方法不能准确揭示芦苇秆热解的动力学过程[29]。因此采用CR法和无函数模型法中的FWO法和KAS法计算芦苇秆热解的动力学参数。通过对3种方法的计算结果进行比较可以看出，CR法比FWO法和KAS法误差大。这是因为在CR法中，求解的活化能只是平均值，而FWO法和KAS法，通过在相同的转化率下建立升温速率和分解温度之间的关系计算活化能，从而能根据相应的转化率得到一系列的活化能。此外，在无函数模型法中，无需假设反应机理，这使得模拟曲线与实验值拟合度更好。而对于无函数模型法，根据表4中的残差平方和可以看出KAS法比FWO法具有更好的吻合度，可能是因为2种方法对温度项处理方式不同造成的，KAS法中温度积分更精确。

3 结 论

3.1 在不同升温速率下，采用热重分析对芦苇秆进行热解特性研究。结果表明：芦苇秆热解可分为4个阶段，第一阶段为干燥阶段，芦苇秆失去自由水；第二阶段发生解聚及玻璃化转变，质量基本不变；第三阶段为芦苇秆快速热解阶段，也是热解过程的主要阶段，在此阶段纤维素、半纤维素等成分热解；第四阶段为炭化阶段，此阶段中木质素热解及剩余挥发分析出。

3.2 将Coats-Redfern法、Flynn-Wall-Ozawa法和Kissinger-Akahira-Sunose法用于芦苇秆热解的第三阶段的动力学分析，将3种方法计算所得转化率(α)与实验数据进行对比，结果发现：当温度为200～250 ℃时，Coats-Redfern法计算值与实验数据吻合度较好，而当温度大于250 ℃时，偏差较大，说明主要热解阶段不是由单一热解反应组成。应用Flynn-Wall-Ozawa法与Kissinger-Akahira-Sunose法计算所得转化率与实验值相比吻合度高于Coats-Redfern法，说明KAS法和FWO法比CR法更适用于芦苇秆热解过程。

3.3 通过主函数图法可知芦苇秆热解最佳反应机理为随机成核，反应级数n=2。Kissinger-Akahira-Sunose 法相比于Flynn-Wall-Ozawa法更适合计算芦苇秆热解动力学参数。Kissinger-Akahira-Sunose 法计算的表观活化能随转化率的增大呈先增大后减小趋势，在220.1～286.9 kJ/mol范围内变化并在转化率为50%时达到最大值。