基于U曲线法的半参数模型中正则化参数确定

周岩，靳奉祥，梁庆华，马德鹏

(1.山东科技大学资源与土木工程系，山东泰安，271019；2.山东建筑大学测绘地理信息学院，山东济南，250101；3.中煤科工集团重庆研究院有限公司，重庆，400039；4.山东农业大学水利土木工程学院，山东泰安，271018)

半参数模型是20世纪80年代初发展起来的一种回归模型，它是将系统误差或者建模近似引起的模型偏差视为非随机参数，采用补偿最小二乘估计法，得到参数和非参数的估值[1-3]，因此，半参数模型广泛地应用于模型精化和减弱系统误差方面[4-5]。半参数模型补偿最小二乘估计中，关键的因素在于如何确定合适的正则化参数α及正则化矩阵R[6]。在测量平差中，正则化矩阵R可根据实际情况按自然样条光滑法、时间序列的特性、先验方差的特性以及观测量之间的某种距离来确定，而正则化参数α的确定方法目前主要有GCV法、L曲线法[7-13]等。GCV法在理论上能够获取最优的正则化参数，但有时GCV 函数的变化平缓，定位其最小值有困难。HANSEN 等[14-15]用L曲线法确定病态问题中的岭估计参数，并详细介绍了L曲线法的基本思想和相关性质；FISCHER等[16-17]在用半参数回归模型处理大地测量数据时，将L曲线法引入半参数模型中确定正则化参数，并进行了相关证明。现有文献表明，L曲线法可以比较容易地获得正则化参数，并且能够得到比较精确的解，但L曲线法在求解过程可能不收敛。U曲线法是根据定义的U(α)函数，即以构成L曲线法的基于正则化参数α>0的信号范数与残差范数为基础，由信号范数的倒数与残差范数的倒数之和组成，以U(α)为纵轴，α为横轴所表示的曲线[18]，其形态接近U 型，共包括3 个组成部分：左边和右边部分几乎是“垂直”的，中间部分几乎是“水平”的，曲线上到原点距离最小的点对应的α或者曲线左侧曲率最大点对应的α即为所确定的正则化参数。通过上述分析，本文作者在简要介绍L曲线法的基础上，详细分析U曲线法，并阐述其相关特性，同时，分别采用L曲线法和U曲线法对模拟数值算例进行求解，通过参数、非参数估计解及单位权中误差的相互对比来分析U曲线法和L曲线法的异同。

1 确定正则化参数的L曲线法

由半参数回归模型L=BX+S+Δ，可得误差方程式为

式中：K为拉格朗日常数；α为正则化参数；R为正则化矩阵。

得

这里正则化矩阵R正定或者半正定，则可求得参数、非参数估计解及单位权中误差，如下式所示[20]：

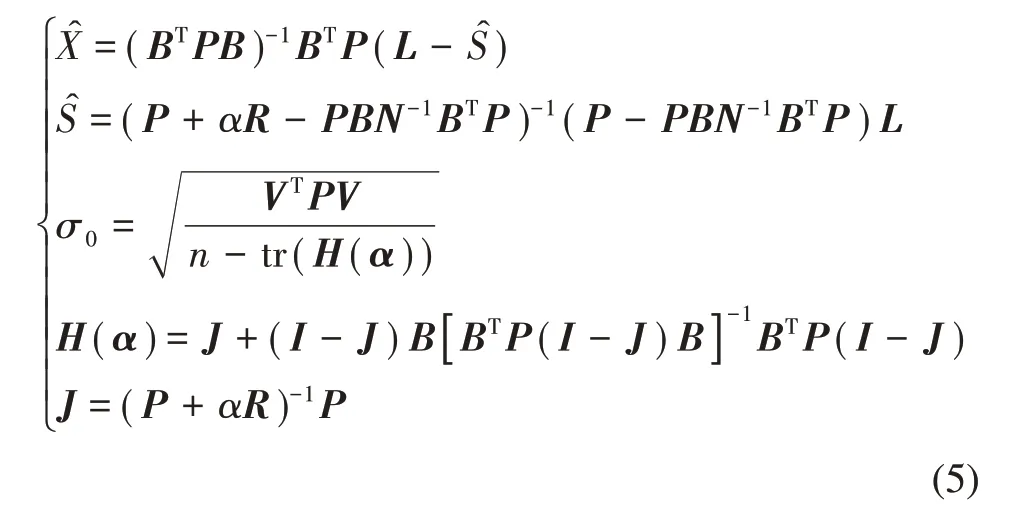
在半参数模型补偿最小二乘估计中，确定正则化参数和正则化矩阵尤为重要，本文在选取正则化矩阵R=GTG的基础上，重点研究不同的正则化参数确定方法对参数估值的影响。

L 曲线法是基于正则化参数α的残差范数和信号范数所表示的曲线，二者都是正则化参数α的函数，选择不同的α，便得到不同的点(Vn(α)，Sn(α))，较为直观的形式就是以Sn(α)为横轴，以Vn(α)为纵轴作图，经拟合得到1条曲线。该曲线包括2个典型部分，分别是“水平”和“垂直”部分，越“水平”部分对应的是正则化参数越小，主要由Sn(α)控制；越“垂直”的部分对应的正则化参数越大，主要由Vn(α)控制；将所得到的类似字母L的曲线称为L曲线。从图1观察信号范数和噪音范数之间是否取得了平衡，或两者是否出现了过大或过小的情况，因此，L曲线法顾及了拟合和光滑之间的平衡，拐点处的值所对应的“角”即为所求的正则化参数的最优解。选取最后的正则化参数值有2种标准：一是选取离原点最近的拐点；二是选取曲率k最大的点。

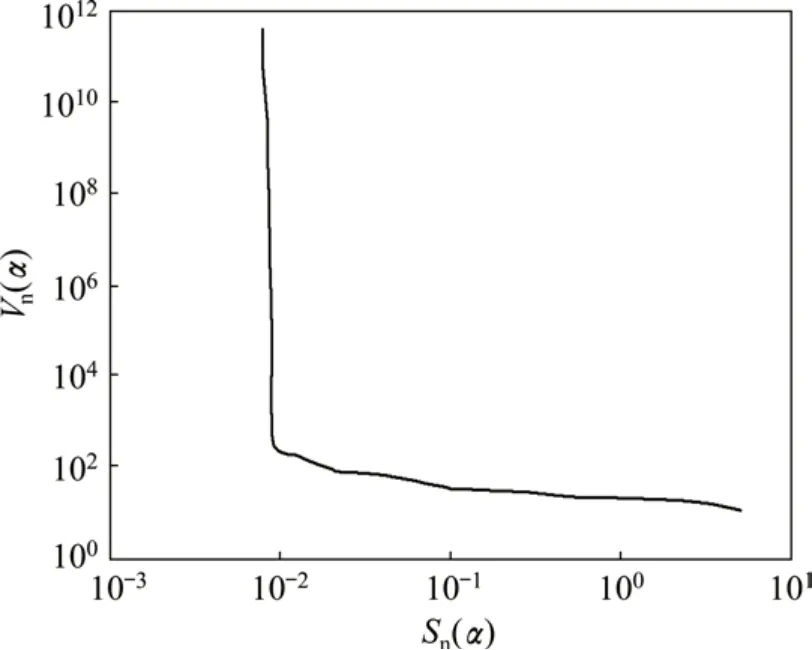
图1 典型的L曲线示意图Fig.1 Schematic diagram of typical L curve

2 确定正则化参数的U曲线法

定义

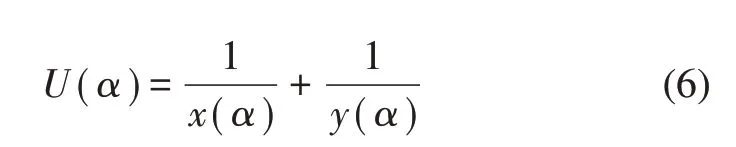
式中：α>0；x(α)和y(α)分别与L 曲线法中Vn(α)和Sn(α)的定义相同。

从图2可见U曲线包含3个典型部分：

1)U曲线在左边部分和右边部分近似垂直。

2)U曲线中间部分近似水平。

3)垂直部分对应的正则化参数是代表了Vn(α)和Sn(α)分别各自主导部分。水平部分对应的正则化参数表征Vn(α)和Sn(α)较接近。

由于x(α)和y(α)分别等同于L 曲线里定义的Vn(α)和Sn(α)，故式(6)可以表示为

对式(7)求导得

图2 典型的U曲线示意图Fig.2 Schematic diagram of typical U curve

1)在L曲线法中，随着α增大，Vn(α)是单调递增函数，Sn(α)是单调递减函数，即在式(8)中，-Sn'(α)>0。由于Vn(α)是单调递增函数，Sn(α)是单调递减函数，根据式(7)和(8)可知，当α较小时，占控制部分的是αSn2(α)，即Vn2(α)-αSn2(α)<0；当α较大时，占控制部分的是Vn2(α)，即Vn2(α)-αSn2(α)>0，所以，U(α)是先减小后增大。

当Vn(α)和Sn(α)这2 部分平衡时，通过U(α)曲线可知U(α)接近水平部分，因此，曲线呈U状，两端近似竖直，中间近似水平。

2)正则化参数的选择。

方法a：

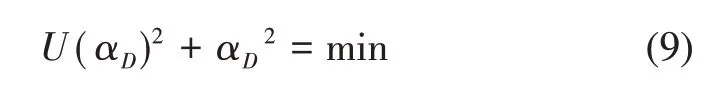
式中：αD为曲线上的点到原点的距离最小时对应的α。

方法b：

式中：αK为曲线左侧曲率最大时对应的α。

3 算例分析

3.1 模拟算例1

设已知P1～P4这4个观测点上的重力异常观测值L及其坐标，如表1所示。观测误差方差DΔ=(0.03)2Ι，试估计已测点重力异常Δg[19]。

物理大地测量中很早就用最小二乘配置法得到重力异常最佳估计值，下面用半参数模型的方法来研究重力异常。在许多地区，重力异常不仅包含随机部分S，而且包含系统部分BX，故重力异常观测方程可写为半参数模型。已有的采用半参数模型求解的文献中，把正则化参数α取为1[20]，也有的采用L 曲线法对正则化参数取值。在这里，采用本文所提出的U曲线法选取正则化参数，并同L曲线法进行比较，同时注意到在重力异常的求解中协方差函数是距离的某种函数，因此，本文中的正则化矩阵采用简单的距离函数，即

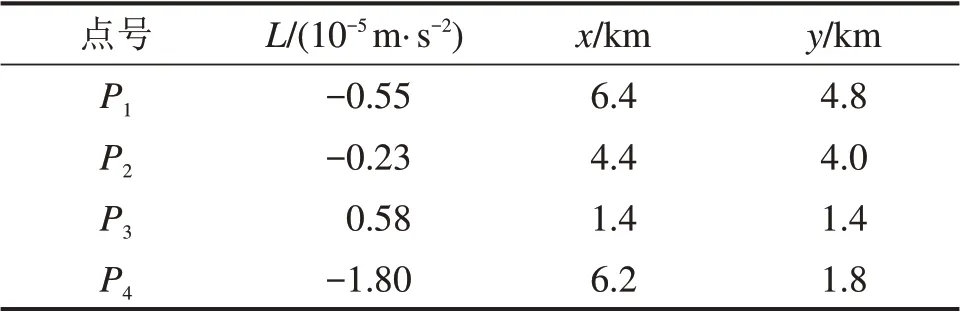
表1 重力异常观测值及其位置Table 1 Observations of gravity abnormity and its locations

函数模型中，重力异常包含随机异常和系统异常2部分。系统部分一般表示为坐标(x,y)的线性函数：

按照半参数模型解算：

L曲线法与U曲线法确定正则化参数的示意图如图3和图4所示，2 种方案计算的重力异常估值差异的比较见表2。

图3所示为纵轴Vn(α)与横轴Sn(α)的关系图，根据其对应的方法得到最佳α的取值，α=1.85。图4所示为定义的U(α)函数(纵轴)与正则化参数α(横轴)的关系图。从图3和图4可以看出U 曲线法比L 曲线法在得到最佳α的取值上计算量要小，而且更直观。

图3 L曲线法确定的正则化参数αFig.3 Determining regularization parameterα according to L-curve method

图4 U曲线法确定的正则化参数αFig.4 Determining regularization parameterα according to U-curve method

由表2可以看出：U曲线法确定的正则化参数使参数估计解的精度要比L曲线法的高，U曲线法计算的重力异常估计结果较接近于文献[19]中的结果，这说明在此算例中，U曲线法求得的正则化参数的可靠性要比L曲线法的高。

3.2 模拟算例2（周期性系统误差）

设L=BX+S(ti)+Δ，B=(Bi,j)100×2，Bi,1=ti，Bi,2=(ti)2，S(ti)=3sin(ti)sin(3ti)，ti=2π(i-1)/100，X=[1 0.25]T，Δ～(0,1)[20]；i=1,2,…,100。

表2 2种方案计算的重力异常估值差异的比较Table 2 Comparison of value difference of gravity anomaly between two calculate solutions

该算例模拟的是周期性系统误差，采用基于正则化矩阵的补偿最小二乘法求解，R矩阵由相邻两观测点模型误差之差的平方和形式确定，设计以下2种方案：方案1，采用L曲线法确定正则化参数；方案2，采用U曲线法确定正则化参数。

这2种方案计算的模拟系统误差的估值与残差估值分别见图5和图6(模拟的残差为模拟参数的真值与模拟系统误差的值代入误差方程得到，半参数估计残差为模拟参数的估值与模拟系统误差的估值代入误差方程得到，下同)。计算所得的X^ 估值与模拟X真值差异的比较如表3所示。

从图5(a)和图6(a)可以看出：当模拟的系统误差呈周期性时，L曲线法和U曲线法确定的正则化参数都使得模拟的系统误差与模拟系统误差的估值变化的趋势基本一致，但U曲线法确定的正则化参数解算得到的系统误差的估值与其真值的吻合程度要比L曲线法的高。从图5(b)和图6(b)可以看出：L 曲线法和U曲线法确定的正则化参数同样也使得半参数估计残差与模拟残差变化的趋势基本一致，并且半参数模型解算观测值的残差经t检验，也都以大于95%的概率服从正态分布。这是由于半参数模型能够将观测值中的系统误差分离出来，减弱其对观测值的影响，从而得到较可靠的参数估值；同时，U曲线法确定的正则化参数解算得到的半参数估计残差与模拟残差的吻合程度也比L曲线法的高。

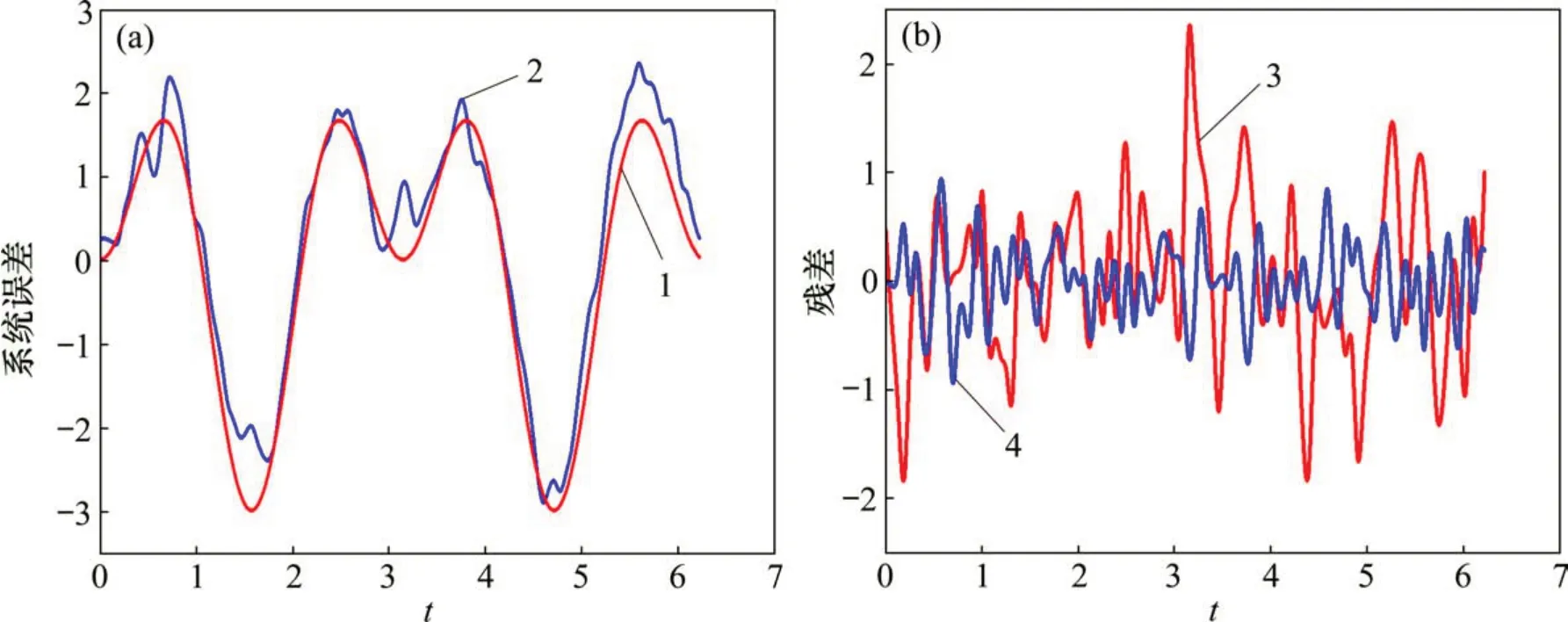
图5 L曲线法确定正则化参数α(周期性系统误差)Fig.5 Determination of regularization parameterα according to L-curve method(system error of periodicity)

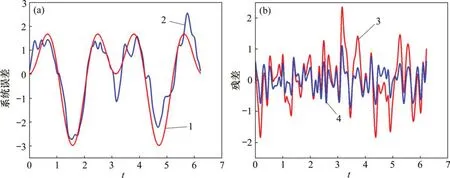
图6 U曲线法确定正则化参数α(周期性系统误差)Fig.6 Determination of regularization parameterα according to U-curve method(system error of periodicity)

从表3可知：L 曲线法和U 曲线法确定的正则化参数差别不大，都能使所求结果与真值较接近，均提高了半参数模型解的精度。但通过进一步对比分析发现：采用U 曲线法得参数估值为[1.011 3 0.235 1]T，与其模拟X真值差异=3.497 0×10-4；采用L 曲线法得到的参数估值为[1.018 0 0238 2]T，与其模拟X真值差异=4.632 4×10-4。与后者相比，U 曲线法确定的正则化参数求得参数估值更接近于真值，表明U 曲线法对正则化参数的确定具有一定的有效性，所得结果具有可信度。

3.3 模拟算例3（线性、周期性系统误差）

为了更接近于实际情况，该算例模拟的是线性、周期性系统误差，采用基于正则矩阵的补偿最小二乘法求解，R矩阵由相邻两观测点模型误差之差的平方和的形式确定，仍设计以下2 种方案：方案1，采用L 曲线法确定正则化参数；方案2，采用U 曲线法确定正则化参数。

这2种方案计算的模拟系统误差的估值与残差估值分别见图7和图8，计算所得的X^ 估值与模拟X真值差异的比较如表4所示。

从图7(a)和图8(a)可以看出：当模拟的系统误差呈线性周期性时，L曲线法和U曲线法确定的正则化参数都能使模拟的系统误差与模拟系统误差的估值较吻合，但U曲线法确定的正则化参数解算得到的系统误差的估值与其真值的吻合程度也明显比L曲线法的高。从图7(b)和图8(b)可以看出：L 曲线法和U 曲线法确定的正则化参数同样都能使半参数估计残差与模拟残差变化的趋势基本一致，但是吻合程度不高。这是因为随着加入系统误差的复杂，半参数模型解算难度增加。但两者相比而言，采用U曲线法确定的正则化参数吻合程度要高。

从表4可以看出：L 曲线法和U 曲线法所确定的正则化参数差异较大，但都能使所求结果与真值较接近，均提高了半参数模型解的精度。通过进一步分析发现：采用U曲线法得到的α为0.095 5，X的估值为=[4.995 7 2.001 0]T，与其模拟X真值差异为=4×10-4；采用L曲线法得到的α为0.715 4，与其模拟X真值差异为=7×10-4。与L 曲线法相比，U曲线法确定的正则化参数求得参数估值更接近于真值。

实验结果表明，L曲线法和U曲线法都可以较好地分离观测值中的系统误差，求得参数的估值；当模拟的系统误差呈周期性或者线性周期性时，U曲线法确定的正则化参数求得参数估值的精度要比L曲线法的高。

表3 2种方案计算的周期性误差下估值与模拟X真值差异的比较Table 3 Comparison of calculatedand simulated valuesX of 2 schemes under periodic error

表3 2种方案计算的周期性误差下估值与模拟X真值差异的比较Table 3 Comparison of calculatedand simulated valuesX of 2 schemes under periodic error

方法L曲线法U曲线法αX^σ0 ΔX^=‖ ‖1.438 4 1.398 1[1.018 0 0.238 2]T[1.011 3 0.235 1]T 1.021 4 0.967 7X^- X 4.632 4×10-4 3.497 0×10-4

图7 L曲线法确定正则化参数α(线性周期系统误差)Fig.7 Determining regularization parameterα according to L-curve method(system error of linear periodic)

图8 U曲线法确定正则化参数α(线性周期系统误差)Fig.8 Determination of regularization parameterα according to U-curve method(system error of linear periodic)

表4 2种方案计算的线性周期性误差下估值与模拟X真值差异的比较Table 4 Comparison of calculated and simulated valuesX of 2 schemes under linear periodic error

表4 2种方案计算的线性周期性误差下估值与模拟X真值差异的比较Table 4 Comparison of calculated and simulated valuesX of 2 schemes under linear periodic error

方法L曲线法U曲线法αX^σ0 ΔX^=‖ ‖0.715 4 0.095 5[4.973 8 1.968 1]T[5.006 5 2.019 8]T 0.953 8 0.509 8X^- X 7×10-4 4×10-4

4 结论

1) 鉴于半参数模型补偿最小二乘估计中正则化参数合理确定的问题，研究了一种新的正则化参数确定方法即U曲线法。模拟算例分析表明采用U曲线法确定合适的正则化参数，能够有效地控制VTPV与STRS之间的平衡，得到了较准确的参数估值。

2) 当模拟的系统误差分别呈周期性、线性周期性时，采用U曲线法确定的正则化参数所求得参数估值和其真值差值向量的范数与L曲线法确定的范数相比分别提高了1.135 4×10-4和3.000 0×10-4。

3) 由于在实际问题中，非参数部分即系统误差或者模型误差具有一定的复杂性，会影响正则化参数的选择。本文提出的U曲线法在一定条件下求得正则化参数使参数估计解的精度较高，在不同条件下，正则化参数的确定要根据相应的情况具体选取合适的方法。