基于层次分析法的公路潜伏风险评价方法研究

鲍彦莅，熊坚，田竞，戴一凡

(昆明理工大学 交通工程学院，昆明 650000; 清华大学苏州汽车研究院 智能网联汽车中心，苏州 215000)

1 引言

近年来，我国加大了对公路和城市道路的投资和建设力度，公路建设里程不断增加。根据国家统计局发布的数据显示，截止2017年底，中国公路网规模达到477.36万公里，其中高速公路13.65万公里。大量研究表明：在导致公路交通事故的诸多因素中，与道路交通环境相关的占23%以上，其中道路条件和交通环境成为诱发交通事故的重要因素。

目前，国内外对于道路交通环境风险方面的研究，主要集中在道路交通环境对交通安全的影响机理研究等[1]。孙文圃，许金良，刘文君[2]用系统工程、统计回归的思想，结合事故资料分别建立高速公路的道路条件、交通条件、立交间距事故预测模型。郝庆宇，熊坚[3]等基于道路交通环境潜伏风险理论分析，确定了道路交通环境潜伏风险评价指标和评价方法。

上述学术研究对于道路交通环境风险研究没有实现完善的定量化分析。本文以公路潜伏风险因素为研究对象，建立公路潜伏风险评价指标，实现对公路交通环境潜伏风险的定量评价。并将评价模型应用于昆石高速，为公路潜伏风险在途预警提供理论依据。

2 公路交通潜伏风险因素分析

公路交通潜伏风险是指在公路交通系统中，由道路条件或交通环境中存在的潜在不安全风险元素所引发的风险[4-5]。本文着重考虑描述公路安全的三个基本因素：风险暴露程度、事故产生风险、事故严重程度[6]，其定义如下：

公路交通潜伏风险=风险暴露程度×事故产生风险×事故严重程度

风险暴露程度=对道路潜在风险的暴露情况进行量化处理

事故产生风险=对车辆产生碰撞的可能性进行量化处理

事故严重程度=对潜在的事故后果进行量化处理

3 潜伏风险评价方法确定

3.1 风险暴露程度评价方法

可采用交通量衡量风险暴露程度，计算方法如用公式(1)[6]所示。公式中将风险暴露程度划分为0到5的等级，分数越高表示风险暴露程度的级别越高。

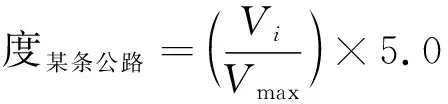
(1)

式中：Vmax为某条公路最大交通量；Vi为该公路特定地点的交通量。

3.2 事故产生风险评价方法

3.2.1 层次分析法确定事故产生风险评价方法

公路潜伏风险中的事故产生风险结合层次分析法，构建事故产生风险评价指标体系。将事故产生风险进行0到5分等级评价，分数越高表示风险等级越高，定义事故产生风险。层次关系如表1所示。

表1 事故产生风险因素

由表1可知，评价目标为事故产生风险等级HRi；评价准则层为道路条件风险R，路边环境风险E，交通设施风险F，气候条件风险C；评价指标层为：各类宏观因素风险包含的信息(ri,ei,fi,ci)。

通过专家问卷打分的方式确定两两评价指标的相对重要性，并结合1-9比例标度法对因素进行标度赋值。本次专家问卷打分邀请了10位交通运输、交通安全领域的专家以及10位智能汽车领域的专家，对准则层中各元素两两比较，对重要性标度赋值。利用特征根法判断矩阵中各元素的相对权重，对判断矩阵进行一致性检验。检验结果如表2所示：

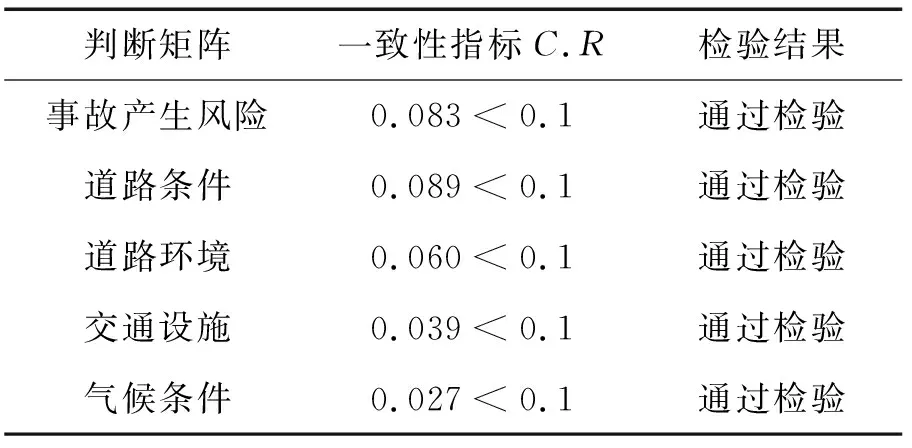
表2 一致性检验结果

由表2可见，判断矩阵一致性均通过检验，符合要求。

3.2.2 建立事故产生风险综合评价模型

通过专家咨询构造判断矩阵后求出的权重系数，建立公路事故产生风险模型如公式(2)所示：

HRi=W1×R+W2×E+W3×F+W4×C

(2)

式中：HRi为路段单元驾驶事故产生风险等级；R为道路条件风险等级，R⊂(r0,r1,r2,r3,r4,r5,r6,r7,r8,r9,r10)；E为路边环境风险等级，E⊂(e0,e1,e2,e3,e4)；F为交通设施风险等级，F⊂(f0,f1,f2,f3,f4)；C为气候条件风险等级，C⊂(c0,c1,c2,c3)；Wj(j=1,2,3,4)为各类风险的权重。通过专家问卷求得的准则层因素的权重如表3所示：

表3 准则层因素权重

道路条件、交通设施、路边环境及气候条件指标层因素的权重如表4所示：

表4 指标层因素权重

R，E，F，C的风险等级根据各类风险信息的权重来确定，其中：权重最大的因素为5级风险；权重最小的因素为1级风险；中间因素权重按插值确定。若不存在上述信息，该类潜伏风险值为0。各因素风险等级的含义：0级为无潜伏风险因素；1级为潜伏风险很小，S=1；5级为潜伏风险很大，S=5；中间值介于两者之间。根据以上定义，设S为某一类因素的风险级别，P为该类风险因素权重，Pmax为该类风险因素最大权重，Pmin为该类风险信息最小权重，则有公式(3)、(4)如下所示：

(3)

(4)

事故产生风险等级值S是介于0和5之间的一个值。设Sij(j=1,2,3,4)分别为单元i路段的道路条件、路边环境、交通设施、气候条件四类风险因素中的某一风险因素等级，因此事故产生风险公式如公式(5)所示：

(5)

式中：单元i的事故产生风险等级HRi为(0,5)之间的一个值。

3.3 事故严重程度评价方法

可以用某条公路的最大限制车速来定量计算事故严重程度[6]，用公式(6)来计算交通事故后果。交通事故后果等级分为0到5，将事故后果定义为Ci：

(6)

式中：PSi为某条公路具体地点的限制车速；PSmax为某条公路最大限制车速。

4 公路潜伏风险等级

针对区域风险或某条公路风险，其潜伏风险等级可以代入RSRIspecific计算，如下公式(7)[11]所示：

RSRIspecific=Ei×HRi×Ci

(7)

式中：Ei为风险暴露程度的风险评价分数；HRi为事故产生风险的风险评价分数；Ci为事故严重程度的风险评价分数。

5 风险评价模型的应用

5.1 评价路段的选取

评价路段选取昆明至石林高速公路(以下简称：昆石高速)，该公路全长78.08 km。路线起于昆明市东郊石虎关，止于石林县石林风景区。自通车以来，昆石高速由于受地形条件、自然环境等多方面的影响因素，交通事故频发。昆石高速的特点是道路线形变化多样，既有符合实验要求的道路线形，又有实验需要的道路环境。此外，昆石高速交通安全亟需提升，选取该路线作为实验线路意义重大。

5.2 收集数据并对评价路段进行风险评价

对评价路段实地调研、收集数据，将昆石高速每5 km一段进行划分，总共划分为16个单元。计算每个单元的事故暴露程度、事故产生风险及事故严重程度，进行潜伏风险评价，同时对每个单元的事故数进行统计，分析风险评价结果及事故数两组数据的关系，计算两组数据斯皮尔曼相关性，若相关性结果接近1，说明风险评价结果与事故数正相关，则评价模型越合理可用。

5.2.1 评价路段风险暴露程度

风险暴露程度与某单元的交通流及该路段最大单元交通流相关。调查得知，昆石高速年平均日交通流量为76698pcu/d，由于该路线长度仅有78.08 km，途中经过七个县级地区，每个单元的流量相近，代入风险暴露程度计算后得到的结果相差甚小，为此本实验中定义每个单元风险暴露程度一致。

5.2.2 评价路段事故产生风险

事故产生风险与道路中存在的潜伏风险因素相关，分析道路现状，结合路段平纵线形，能够获取风险因素，将每一单元的风险因素带入公式(5)，计算得到最大等级为5，最小级别为1的事故产生风险。其评价结果如图1所示：

图1 昆石高速事故产生风险

由图1可见，事故产生风险较高的单元分别为：K0-K5，K5-K10，K45-K50三个单元，其事故产生风险等级分别达到了4.07，5.00和4.16。其中，K0-K5、K5-K10及K45-K50两个单元均属于此类道路环境复杂多样的路段，其事故产生风险等级较高。

5.2.3 评价路段事故严重程度

事故严重程度与某单元限制车速及该路段最大限制车速相关，获取每个单元的限制车速以及昆石高速的最大限制车速，带入公式(6)，计算得到事故严重程度，事故严重程度最大为5，最小为3.75，结果如图2所示：

图2 事故严重程度

由图可见K5-K25，K30-K35，K50-K80路段限制车速均为120 km/h，由于车速越高，驾驶者越难应对突发状况，其发生事故的严重程度越严重，因此这些路段的事故严重程度计算结果均为5；而K35-K55路段其限制车速为90 km/h，是整个评价路段中限制车速最小的路段，因此这部分的事故严重程度较小，等级为3.75；其他路段限速为100km/h，计算所得事故严重程度为4.17。

5.2.4 评价路段潜伏风险评价

公路潜伏风险由事故暴露程度、事故产生风险以及事故严重程度相乘所得，可以用公式(7)来进行计算，计算所得的公路潜伏风险是一个0-125的数值。为了使得风险数据更加直观易接受，此处将公路潜伏风险归一化处理，转化为0～100的数值，如公式(8)所示,计算结果如图3所示：

(8)

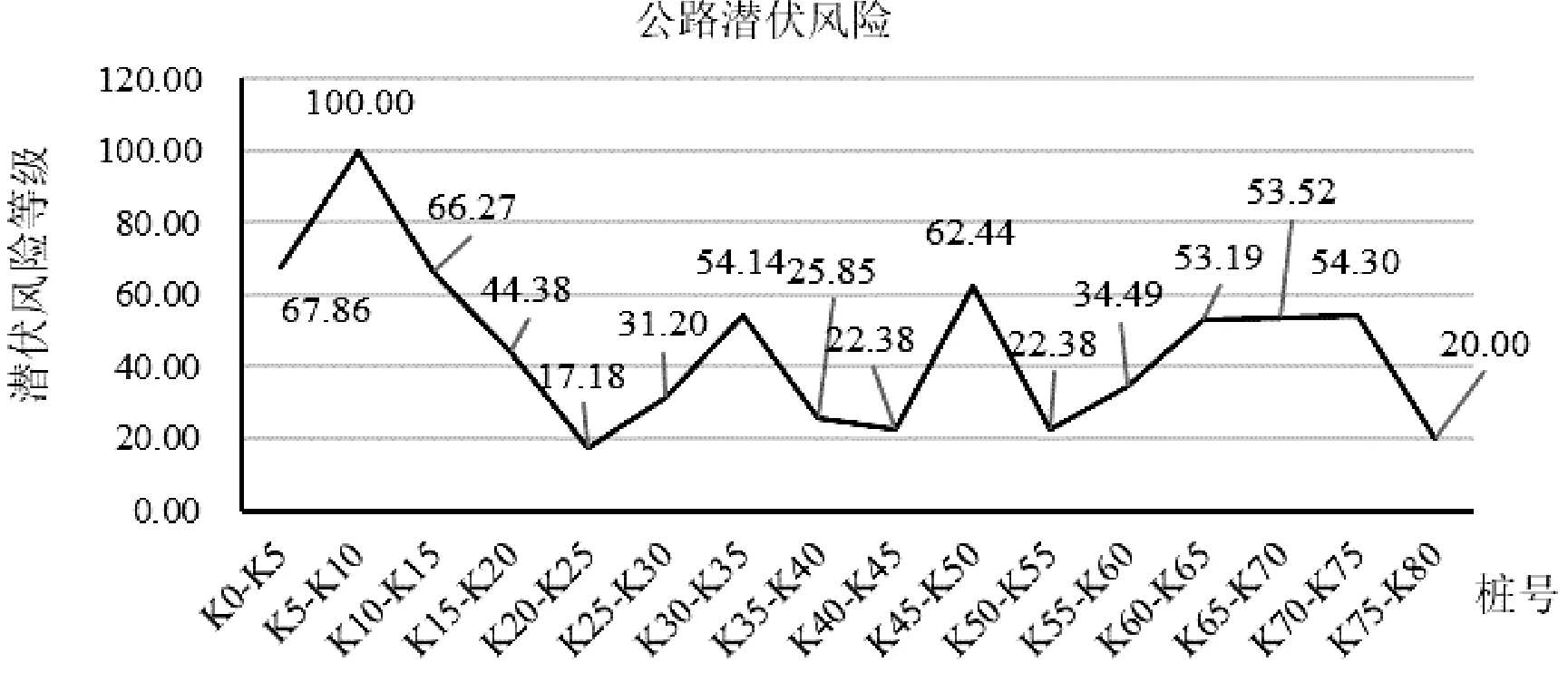
图3 公路潜伏风险等级

由图3可见，公路起点的公路潜伏风险值偏高，其中K0-K5、K5-K10、K10-K15公路潜伏风险值分别为67.86、100.00、66.27。随之风险值逐渐降低，在K20-K25处达到最低，风险值为17.18。

5.3 风险评价与事故统计对比

为了验证公路潜伏风险等级评价的合理性，将评价路段风险等级与该路段5年事故数进行对比分析。考虑到该路段暴露风险相同，忽略事故严重程度(没有对比数据)，将公式(5)计算的事故产生风险等级与该路段2007～2011年共5年的统计事故进行对比，对比结果如图4所示：

图4 事故产生风险与事故数对比折线图

由图4可知，KO-K5，K5-K10，K45-K50三个单元其事故数均大于90，公路潜伏风险等级均大于4级，评价结果与真实事故情况基本一致。K20-K25，K40-K45，K55-K50，K75-K80四个单元事故数均小于50，其公路潜伏风险等级均小于2级，评价结果与真是事故情况相接近。而K35-K40，K50-K55，K70-K75三个单元的事故数与公路潜伏风险评价结果相差较大。其中K35-K40的事故数为81，而公路潜伏风险等级只有1.72；K50-K55的事故数为73，公路潜伏等级只有1.49；K70-K75的事故数为35，但公路潜伏风险等级却达到了3.76。其他单元评价结果与真实事故数据虽有差别，但差别不大且趋势相近，评价结果比较合理。

6 讨论

将昆石高速事故数进行归一化处理，使成为0～5之间的一个值，得到风险预测值。对比风险预测值与风险评价等级之间的差别，计算两者之间的差值，差值越小说明评价结果与事故数越接近，其中风险预测值计算如公式(9)所示：

(9)

计算结果如表5所示：

表5 风险预测值与事故产生风险等级差值对比

由表5可见，K35-K40，K50-K55，K70-K75三个评价结果与事故数相差较大的单元中，K35-K40，K50-K55两个单元的均属于潜伏评价结果偏小而真实事故数偏高的情况，而K70-K75单元潜伏风险评价结果远大于真实事故数据。

据分析，K35-K40单元整段道路5km，其中阳宗隧道位于K37+475至K40+440，全长2.7 km。对阳宗隧道进行调研及现场踏勘分析，该隧道是事故频发点，行车视线不佳，导致此路段事故率较高。潜伏风险评价模型中，虽考虑隧道对道路安全的影响，但没有对隧道长度、隧道内光线加以细分评价，因此此处评价与事故数据有偏差。

K50-K55单元属于连续长下坡路段K48-K55的终点处，且存在不少坡度大于3%的纵坡。本文从宏观层面计算了纵坡对车辆的影响，但未细分至连续长下坡对道路安全的影响权重，因此评价分数相对于事故数较低。

K70-K75单元，处于2车道路段，相对于道路之前3车道路段，风险相应降低。同时，该路段道路防御设施完备，降低了道路存在的风险。由于公路潜伏风险评价模型中没有考虑不同车道数、道路宽度以及标志标牌对道路潜伏风险的影响，因此该单元潜伏风险评价等级比实际事故数偏高。

本文采用斯皮尔曼相关系数来检验事故数与风险等级两组数据的相关性。该方法采用单调方程来评价相关性，如公式(10)所示：

(10)

式中ρ是衡量事故数与风险等级两个变量相关性的非参数指标，当两个变量完全单调相关时，ρ=±1。此处计算得到相关性达到ρ=0.6418。由此可见该评价模型可以用于评价公路潜伏风险，能够反映道路的安全性。

7 结论

(1)本文将公路及环境中存在的潜伏风险因素进行了量化，建立了公路风险评价等级模型；对风险评价模型与实际事故统计数据对比分析表明，该模型与事故发生率基本一致。

(2)该模型对路段单元风险具有较强针对性，可用于一条道路的风险定量评价；该模型可用于在建公路的风险预评估，也可用于现有道路的风险评估。

(3)若进一步细化路段风险因素，如隧道长度、连续长下坡、道路线形组合，公路标志标线等因素，在今后大数据背景下，可对对模型进行修正，以得到更加准确的风险评价模型，增加模型应用的有效性。