大气层外多拦截器协同跟踪与制导算法

张 召，王 恒，荆武兴，高长生

(哈尔滨工业大学航天学院，哈尔滨 150001)

0 引 言

为降低对弹道导弹中段目标群识别技术的需求，美国导弹防御局提出一种多拦截器(Multiple kill vehicle，MKV)技术[1-2]。它通过运载器将一个携带多枚微小型拦截器(Kill vehicle，KV)的母舱送至指定位置，然后释放拦截器对一定范围内所有目标进行打击[3]。针对上述场景，本文重点研究多拦截器对多目标的协同跟踪以及协同制导问题。

多传感器对多目标的协同跟踪[4-5]，一般包括传感器管理和多源信息融合两个内容。在MKV作战中，传感器管理和拦截器管理是耦合在一起的，甚至后者优先级更高，属于武器目标分配问题(Weapon-target assignment，WTA)[3,6]。在完成WTA后，传感器分配的操作空间不大，本文将研究重点放在了多源信息融合上。

拦截器配备的红外导引头，可以提供自己目标及其临近目标的角度信息[7]。但相应的可观测性较低，对目标状态的估计精度不高[8]。多传感器信息融合，是提高估计精度的有效方法。从结构上看，多源信息融合可分为3种[9]：集中式测量融合，分布式状态融合和混合式融合。集中式测量融合架构的核心是信息融合中心，它接收所有传感器的测量数据并负责所有的数据处理工作，如此可以有效利用探测信息，形成全局最优的估计结果。然而，集中式方法存在着一些缺点，比如生存能力低、可靠性低、较重的通信负担和计算消耗[10]。分布式状态融合根据各传感器对观测目标的测量数据，分别进行滤波跟踪，生成多个局部航迹，信息融合中心接收所有的局部航迹，对各局部航迹进行数据关联和融合等处理。如此减小了网络通信压力，避免了大范围网络不确定性问题，但仍存在传感器不确定性问题[11]。混合式融合结构兼具上述两者的优点，但缺点是通信带宽和计算量更大。为满足大气层外多传感器信息融合的要求，需要综合以上结构的特点，重新设计融合结构。

同时需要注意，以传感器网络的形式进行工作，需要处理以下不确定性问题：网络延迟、丢包以及测量丢失(或者传感器故障)。一般而言，这些不确定性可以用随机参数进行描述[12]，比如一个四维状态马尔科夫链[13]或三个伯努利随机变量[14]，然后基于这些随机参数的描述，使用新息分析的方法可以推导出一些次优和最优的滤波算法[12]。其中一个比较重要的问题是，出现故障的传感器如果不能即时诊断和隔离，会造成随即变量相关性问题，严重影响信息融合的精度和稳定性。一些学者的处理办法是改变随机变量的模型[15]，而这又会涉及到模型结构和参数的设计问题。为保证信息融合的稳定性，亟需开展针对大气层外传感器网络的故障诊断和隔离研究。

多拦截器对多目标的协同制导，是指各拦截器之间在飞行中相互配合，遵循某种战术策略意义上的运动学规律，共同完成制导任务[16]。协同制导的研究主要集中在实现制导时间、空间或功能上的协同一致性。当前热点集中在无人机协同问题、平台问题、反舰以及防空问题等[17-18]。主要有两种协同方式，隐式协同和显式协同[19]。在隐式协同中，飞行器之间通过设置一些参数来实现协同，比如要求拦截器以一定的角度拦截目标；而在显式协同中，则需要优化一些团队性能指标，例如需要多枚拦截器保持一定的几何构型。相对来说，隐式协同设计方法较为简单，静态或动态地给各个飞行器分配协同参数，然后以带约束方式设计其制导律即可；而显式协同需要考虑的约束更多，本文不做研究。一般而言，带约束的制导可以看作是经典比例导引的衍生算法，相应的设计方法有滑模控制、最优控制、微分对策、线性二次型调节器等[19-21]。然而，该领域研究大多针对大气层内飞行器，而且需要连续可变控制力，这是大气外飞行器所不能提供的。兰伯特制导虽能实现时间控制，但是需要拦截器以速度突变方式工作，与实际的有限推力不符。随着MKV技术的发展，为避免拦截作战相互间的干扰，对多目标实现同时击毁的需求越来越迫切，需要对此时间协同制导进行研究。

针对上述多源信息融合、传感器故障、大气层外时间协同制导三个问题，本文进行了细致的研究。首先，提出各拦截器与其周围数个拦截器共享测量数据，进行局部集中式测量融合的策略，以避免红外测量信息不完全和全局融合造成的大范围网络不确定性问题；然后，对于传感器故障，本文将研究的重点放在了诊断和隔离上，使用残差检验的方法，及时隔离出现故障的传感器，排除其对估计的影响；最后，为实现时间协同，本文以隐式协同的方式预设各个拦截器的打击时间，并以此为约束结合相对运动解析解设计其制导律，保证多枚拦截器在同一时间击中各自的目标。

1 问题描述

在MKV技术研究上比较成熟并且取得了初步研究成果的机构主要有，洛克希德马丁(Lockheed Martin Space Systems Company)和雷神(Raytheon Company)两家公司，其方案分别称为MKV-L[22]和MKV-R[23]系统。以MKV-R为例进行问题描述，其由一组完全相同的拦截器组成，每个都有同样的传感器、数据链、软件和推进系统。母舱携带多枚拦截器构成有效载荷，由助推火箭运送至大气层外指定位置。之后，母舱经由数据链获取威胁评估，并适时释放第一枚拦截器。随后该拦截器立即开启红外导引头获取目标信息，并辅以数据链信息，快速估计分析战场敌我双方的态势。捕获确认敌方多个目标后，控制和引导陆续发射的拦截器攻击不同目标(即WTA)，如图1所示。最后，各拦截器导引头对准各自目标，由轨控发动机进行轨道控制实施拦截。

由于弹目距离远大于敌方目标群散布尺度，一个目标可能会进入多个拦截器的视场，经数据共享和数据关联处理后，可以获得针对该目标的多批次探测数据。为了缓解角度测量可观测性低造成的估计精度差，研究对该多批次探测数据进行多源信息融合，为制导系统提供精确的目标信息；同时考虑到可能出现的传感器故障，结合滤波框架设计故障诊断隔离算法，排除其对估计效果的干扰；最后为了避免爆炸对临近拦截器的干扰，需要保证多拦截器时间协同一致性，以打击时间为约束设计各拦截器的制导律。

2 多拦截器协同跟踪算法

以临近的多个拦截器的红外探测数据为基础，通过最小二乘算法对指定目标进行几何定位(Geometry positioning，GP)，实现初步的信息融合。之后，基于伪测量信息设计非线性跟踪滤波算法，对目标状态进行更加精确的估计。最后，依托滤波框架，设计残差检验算法，对出现故障的传感器进行诊断和隔离，排除其对估计效果的干扰。

2.1 多拦截器协同定位

基于多个拦截器红外导引头的探测数据，对目标进行几何定位。假设目标位置为r=[x,y,z]T，拦截器位置为ri=[xi,yi,zi]T，则相应的角度关系为：

(1)

式中：αi为方位角,βi为高低角。对式(1)进行整理，可得：

(2)

写成矩阵形式为：

Mr=Y

(3)

式中：

通过最小二乘算法对上式进行求解，可得：

r=(MTM)-1MTY

(4)

在实际应用中，会存在测量噪声。因此，不仅需要对目标进行定位，而且需要提供定位误差的统计信息。基于上述结果，并结合误差传播规律，可以确定几何定位结果的误差协方差。假设初始的测量方程为：

θ=h(x)+vθ

(5)

r*=(MTM)-1MTY

(6)

式中：

M=

Y=

(7)

(8)

(9)

同理，可得：

(10)

(11)

根据误差传播公式，可得：

(12)

式中,⊗表示Schur乘积(元素对元素相乘)。

考虑到各个传感器是相互独立，可以忽略测量之间的相关性，则定位误差协方差可以简写为：

Rz≈diag(σr*⊗σr*)

(13)

则初始的非线性测量方程，变为线性测量方程：

z=Hx+vz

(14)

(15)

2.2 基于无迹卡尔曼滤波的目标跟踪

考虑到状态方程为目标的动力学方程，仍为非线性方程，本文采用基于无迹变换(Unscented transformation，UT)的无迹卡尔曼滤波(Unscented kalman filter，UKF)[24]，实现对目标状态的估计。系统模型如下：

(16)

UKF滤波的递推公式可以表示如下。

1)初始状态统计特性为：

(17)

2)设计UT的采样策略。

γi,k|k-1=fk-1(ξi,k-1),i=0,1,…,2n

(18)

(19)

(20)

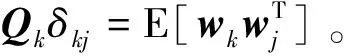
4)测量更新。考虑到测量方程已经线性化，直接使用线性卡尔曼滤波(Kalman filter，KF)的测量更新：

(21)

(22)

(23)

2.3 基于残差检验的故障诊断

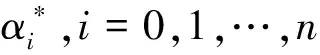
(24)

得方位角的预估值为：

(25)

方差可以表示为：

(26)

将真实的测量值与预估值作差，若超出均方差：

(27)

则认为出现故障，剔除该拦截器提供的信息。

同理，可以基于高低角信息进行故障诊断，在此不再赘述。

将上述故障诊断算法，融入前文的UKF算法，形成故障诊断无迹卡尔曼滤波(Fault diagnosis unscented kalman filter，FDUKF)算法，如图2所示，可以实现较为稳定的跟踪。

3 多拦截器协同制导算法

为实现时间协同打击，本文将制导过程分为两个阶段：控制打击时间的中制导以及消除脱靶量的末制导。其中，中制导律设计思路是：基于推导的动力学解析解(称为制导动力学模型)，以预设打击时刻弹目距离为零为指标，设计当前时刻的指令推力。由于中制导的消耗，末制导阶段的轨控能力有限，有必要研究以一次点火消除脱靶量的策略，则点火时刻的设计至关重要。因此，末制导律的设计思路是：以动力学解析解为基础，以轨控发动机关机时刻弹目进入零控拦截流型为指标，设计发动机的点火时刻。

3.1 基于时间协同的中制导算法

弹目相对运动模型如下：

(28)

式中：rm、rt分别为拦截器位置rm和目标位置rt的模；ac表示拦截器控制系统产生的加速度，在工作时间内视为常值；μ为地球引力常数。

(29)

式中：v=vt-vm,r=rt-rm。解式(29)方程得：

(30)

式中：r(t0)和v(t0)分别为当前时刻t0弹目相对位置和相对速度，r(t)和v(t)分别为t时刻弹目相对位置和相对速度。以此为基础，进行中制导律的设计。

假设发动机于当前时刻t0点火，关机时刻为tb，预设打击时刻为tf。其中，发动机关机时刻由发动机特性决定，预设打击时刻可根据分离前弹目轨道的脱靶时刻进行设计。在t0至tb时间段内，指令加速度ac为常值，则由式(30)可得：

(31)

发动机关机之后，拦截器以零控方式飞行，即在tb至tf时间段内，ac=0，可得：

(32)

时间协同制导要求r(tf)=0，联立式(32)可得当前时刻指令加速度：

ac=-A/B

(33)

式中：

cosω(tf-tb)+[-r(t0)ωsinω(tb-t0)+

由指令加速度ac可以计算得到指令推力Fc。在每个采样周期内计算Fc，并进行阈值判断，当Fc的模大于阈值时则发动机点火；若发动机已经处于工作状态，则需根据最新计算结果调整推力方向。

3.2 基于零控拦截流型的末制导算法

进入末制导后，拦截器需要对准目标，轨控系统只能提供侧向力，即：

(34)

则可得指令加速度为：

(35)

式中：fc为发动机额定推力，m1为拦截器质量,r1和v1为点火时刻t1的弹目相对位置和速度。那么，该阶段制导律主要是设计发动机的点火时刻t1，以进入零控拦截流型，过程如下。

在当前时刻t0至点火时刻t1内，ac=0，可得：

(36)

在点火时刻t1至关机时刻tb,ac由式(35)确定，可得：

(37)

式中：下标b表示关机点。

发动机关机后进入零控拦截流型的条件为：

(38)

联立，经推导可得：

(39)

经少量迭代可求解式(39)，进而确定点火时刻t1。

4 仿真校验

设计如下场景：包含1个母舱、8个KV及其对应的8个目标；每个KV重5 kg，装药0.5 kg，共4台固体轨控发动机，每台发动机推力为61 N，持续工作2.5 s；在J2000.0坐标下描述，132 s时刻开始中制导，弹目距离约500 km；此时母舱状态(位置km、速度m/s)为[2017.6, 7551.3, 31.8, 2778.5, -1271.2, 330.4]T，各个KV靠自身轨控发动机于此点分离；此时目标运载器状态为[2460.9, 7444.1, 234.8, -3815.6, 304.1, -2693.5]T，各个子目标以其为中心构成一个直径8 km的目标群；弹目距离进入200 km后，开启末制导。

以1号KV对1号子目标为例，对协同跟踪进行分析。以临近的5个KV传感器的探测数据为基础，使用前文设计的算法进行协同定位。然后依托常速度(Constant velocity，CV)、常加速度(Constant acceleration，CA)、制导动力学(Guidance dynamic，GD)模型和对式(28)的二阶离散动力学(Second-order discrete dynamics，SD)模型，设计跟踪算法。其中，前两者使用KF即可，形成CVKF和CAKF；后两者需要使用前文设计的UKF算法，形成GDUKF和SDUKF。进行蒙特卡洛仿真，以位置均方根误差(Root mean square error，RMSE)为指标进行评估，结果如图3所示。

从图3可以看出，随着弹目距离的减小，GP的精度逐步提高，相应的跟踪精度也逐步提高。但是以CV为模型的跟踪出现了发散的情况，这是由于模型不匹配造成的。其余的三个估计器精度差别不大，均可实现较为精确的跟踪。对整个跟踪过程的位置RMSE取均值和均方差，如表1所示。可见，以本文设计的制导动力学模型进行跟踪，RMSE均值最小，发散程度最小，为后文所采用。

表1 跟踪模型分析Table 1 Analysis on tracking model

传感器故障的一种表现是输出异常，即数据偏离正常值，这将会干扰估计结果。在170 s时刻，一个临近KV的传感器出现故障，持续时间1 s。根据前文设计的故障诊断算法对其进行诊断隔离，与不进行诊断隔离的跟踪进行比较，如图4所示。可以发现，当故障出现时，GP算法出现了较大的误差，同时引起UKF算法的发散。原因是故障传感器输出异常，造成GP结果异常，并输入到滤波器；此时的滤波器已经趋于稳定，稳定的滤波增益权衡模型和测量的不确定性给出估计结果；然而异常数据的统计特性，并不符合预设的测量不确定性描述，滤波增益无法及时调节，造成异常数据将估计结果拉偏的情况。由于设计了故障诊断功能，FDUKF则可以及时检测出故障传感器的异常输出并将其隔离，避免了估计结果的发散，保证了估计精度和稳定性，详细数据如表2所示。

根据分离前弹目轨道的脱靶时刻，设计预设打击时刻为200 s时刻，基于以上跟踪和协同制导律，对1号拦截器的轨道进行控制，如图5和图6所示。中制导过程，150 s时刻以后计算得到的指令推力逐

表2 传感器故障诊断分析Table 2 Analysis on the sensor fault diagnosis

步上升，直至超过阈值，轨控发动机点火；由于发动机的控制，预测打击误差减小，并保持在一个较小的范围内，如此可以有效控制打击时间。末制导过程，制导指令是轨控发动机的点火时刻，若计算得到的点火时刻在当前时刻之前，则发动机立即点火；若在当前时刻之后，则需要等待，等待过程中仍然要根据跟踪数据不断更新点火时刻；发动机关机后，弹目进入零控拦截流型，如此可以有效减小脱靶量。最终的时间偏差为0.0876 s，脱靶量为0.3228 m。

使用蒙特卡洛仿真算法，对整个拦截场景进行分析，拦截效果(时间偏差和脱靶量)如表3所示。由表3可知，对打击时间的控制较为精确，将时间偏差控制到了0.1 s以内；脱靶量的控制较差，控制到了0.5 m左右，这与末制导的制导周期以及轨控发动机的工作模式有很大关系。同时，可以看出制导律设计时并未考虑跟踪结果的不确定性，这势必造成制导指令的波动，引起发动机能量的损失，需要进一步研究。

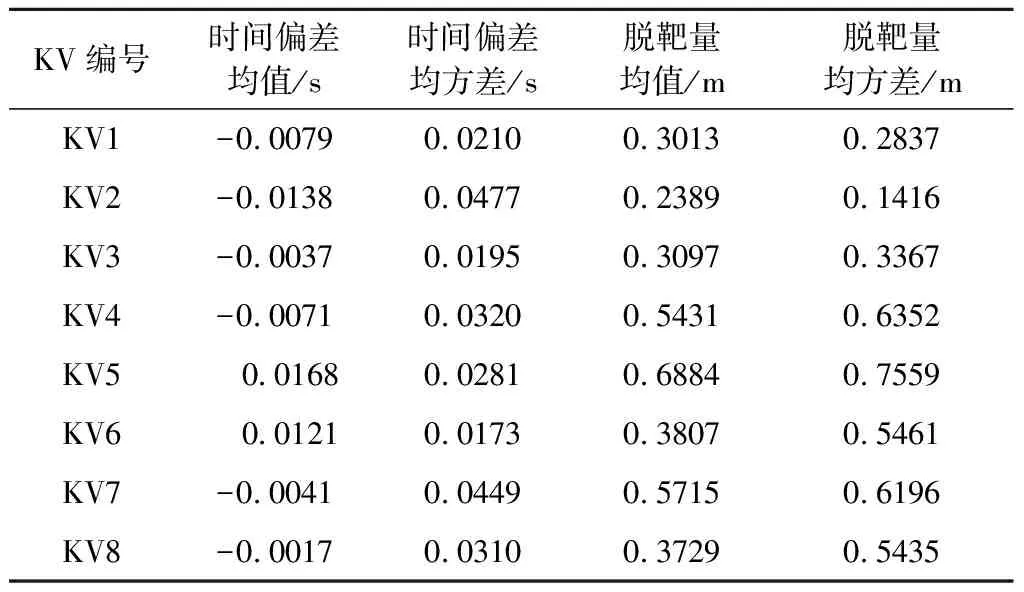
表3 拦截结果分析Table 3 Analysis on interception results

5 结 论

本文对大气层外多对多拦截中涉及到的协同跟踪和协同制导问题进行了研究，提出了带故障诊断的协同跟踪算法、时间协同中制导律以及消除脱靶量的末制导律，得出了以下结论：1)详细推导了以最小二乘算法为基础的协同定位算法，并研究了其误差传播规律，实现了局部信息融合以及测量方程的线性化；2)设计了基于残差检验的传感器故障诊断算法，可以有效保证信息多源融合结果的稳定性；3)基于简化的动力学模型，设计了有限推力下的时间协同中制导律和消除脱靶量的末制导律，可以完成对多目标的同时击毁。