二次Riccati方程不变量解法的进一步研究*

赵 临 龙

(安康学院数学与统计学院，陕西 安康 725000)

0 引 言

1841年，Liouville证明了二次Riccati方程：

L[y]=-y′+P(x)y2+Q(x)+R(x),
(P(x)R(x)≠0),

(1)

其中P(x),Q(x),R(x)为连续函数.一般不能通过初等积分法求得方程(1)的初等函数表示的解.但在实际工作中，又急迫需要方程(1)的精确解，如在微分方程中，三阶Schwartz微分方程、kdv方程，以及科学问题中的扩散问题、鲁棒稳定性等，使Riccati方程依然成为具有挑战性的世界难题[1-2].

近三年来，有关Riccati方程研究文献不少[3-14].国内外学者利用各种研究方法确定方程(1)的精确解，是方程(1)研究的主流[1].如在文[8]中，对于Riccati方程求解，通过G′/G展开法，得到了Riccati方程形如G′/G的解，但其过程较复杂.现对Riccati方程求解再作讨论.

对于方程(1)，如果能找到该方程的一个特解函数y0，即L[y0]=0，则方程(1)化为可解的Bernoulli方程[2].但Riccati方程的特解y0一般较难求.我们将针对Riccati方程的一个非特解函数y0，即在L[y0]≠0的条件下，给出Riccati方程的求解过程.

1 Riccati方程可积性理论

1998年，赵临龙提出Riccati的不变量概念，并且利用不变量概念，给出了Riccati的解法[13-14]，引起了广泛关注并多次被引用.

为简化推理过程，我们将函数P(x),Q(x),R(x)，简记为函数P、Q、R.

定义1[2]在Riccati方程(1)中，称为方程(1)的不变量.

定义2[2]在Riccati方程(1)中，称为方程(1)的广义不变量，其中y0(x)为方程(1)的非特解函数.

定理[14]在方程(1)中，如果存在常数α,β,γ，以及函数y0(x)和可导函数G(x)(其中G(x)≠0)，满足不变量关系：

I1=P(x)L[y0(x)]=αγG2(x),

(2)

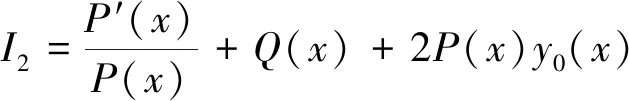
(3)

则方程(1)经线性变换：

y=φ(x)z+y0(x),φ(x)=αG(x)/P(x),
(其中φ(x)≠0)

(4)

可化成其积分形式：

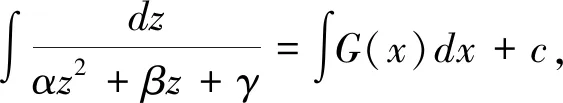
(5)

2 Riccati方程求解过程

在定理中，对于寻找非特解函数y0，确定Riccati方程(1)对应的函数L(y0)，成为解决实际问题的关键.

利用不变量关系式(2)和(3)，给出一种确定非特解函数y0的较简单方法.

此时，假如满足不变量关系式(2)的非特解函数y0，使得函数L(y0)满足:

I1=P(x)L[y0(x)]=αγΔ,(Δ为常数),

(6)

则不变量关系式(3)满足：

(7)

此时，非特解函数y0满足：

(8)

在(8)中，取特例β=0，则非特解函数y0满足：

(9)

推论1对于Riccati方程(1)，如果非特解函数y0满足：

(10)

则方程(1)经线性变换：

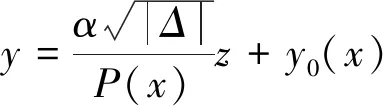
(11)

化成积分形式：

(12)

推论2对于Riccati方程(1)，如果函数y0满足(10)，则当L[y0]=0时，方程(1)的解是：

(13)

此时，由于L[y0]=0，则满足(10)的函数y0，对应于方程(1)的不变量关系结果为：

I1=P(x)L[y0(x)]=0=αγG2(x),

(14)

(15)

可取α=-1,β=0,γ=0,G=1，于是，有积分形式：

(16)

则原方程的解是：

(17)

3 应用举例

针对文[8]的Riccati方程，给出新的解法，以显示本方法的优越性.

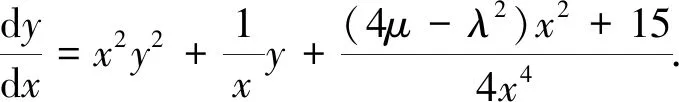
记Δ=λ2-4μ，由于

于是，得到：

则原方程的解是：

则原方程的解是：

记Δ=λ2-4μ，由于

于是，得到：

按例1的方法，可以求得原方程的解.

可见，该方法求解Riccati方程(1)，关键是求满足关系式(9)的非特解函数y0，使函数L[y0]满足关系式I1=PL[y0]=Δ(Δ为常数).

例3[8]研究如下方程:

在例3方程中，记Δ=λ2-4μ，由于

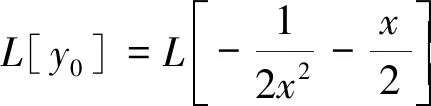
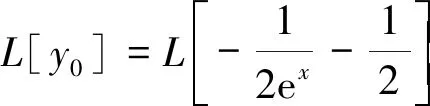
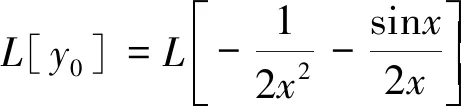
例4[15]求解微分方程：(2x+1)2y″-4(2x+1)y′+8y=0.

解：令y=eu，则有

(2x+1)2(u″eu+u′2eu)-4(2x+1)u′eu+8eu=0,

(2x+1)2u″+(2x+1)2u′2-4(2x+1)u′+8=0.

(18)

令u′=z，则有

(2x+1)2z′+(2x+1)2z2-4(2x+1)z+8=0,

(19)

(20)

=0.

I1=PL[z0]=0，可取α=-1,β=0,γ=0,G=1，则方程(20)的解是：

4 结束语

综上，对于Riccati方程(1)的求解，仍然是具有吸引力的学术问题，寻求非特解(或特解)函数y0，使构成的函数PL[y0]为常数的求解，是一条可行的路径.