物理化学实验数据处理过程中拟合函数问题的探讨*

段雨爱 王 前 廖 奕 魏留芳

(1. 首都师范大学化学系，北京 100048； 2. 北京师范大学朝阳附属学校，北京 100048)

0 引 言

物理化学实验是理科化学相关专业大学本科教学的一门重要的基础必修实验课程，与其他实验课程不同的是，物理化学实验主要通过仪器测量得到一系列实验数据，这些数据均为间接数据，需要学生进一步对数据进行处理，处理的过程一般包括数据的记录、整理、分析、计算、以及用图形描述等，由此得到最终的结果参数[1-2]．通常处理的方法有：根据公式计算进行转换，线性拟合，求拟合方程以及截距和斜率，或非线性拟合，作切线，求截距或斜率，依实验数据作图等．在一系列的数据处理过程中，拟合函数的选取对数据处理的精确与否起到至关重要的作用[3-4]，拟合函数不同会对实验结果产生不同的影响，拟合函数选择不当会引入不必要的人为计算误差．因此，选择正确的拟合函数进行数据处理对减小实验误差十分重要．

本文以胶体化学和表面化学部分的最大泡压法测定溶液的表面张力实验作为研究对象，采用Origin数据处理软件[5-7]，选取3种常用的拟合函数对实验数据进行后续处理，比较不同拟合函数对实验结果的影响，最终选取较为合理的拟合参数．

1 实验方法

室温下，采用最大泡压法测定不同浓度的乙醇水溶液的表面张力[8]．目前测定液体表面张力方法有多种, 如：毛细管上升法，Wilhelmy 盘法，旋滴法，悬滴法、滴体积法、最大气泡压力法等[9-10]．与其他方法相比，最大泡压法测定溶液表面张力实验的装置比较简单，操作方便，且无需考虑接触角的影响[11].在气泡生成的过程中，由于表面张力的作用，凹液面会产生一个指向液面外曲率中心的附加压力(Δp)，而附加压力与表面张力(γ)成正比，与球形气泡的曲率半径(R)成反比：

Δp=2γ/R．

当R与毛细管半径(r)相等时，附加压力最大，可通过与之相连接的压力计读出压强(P)的大小，即P=ρgΔh，其中ρ为密度，g为重力加速度，Δh为液面高度差．由此计算表面张力公式为：

由于实验过程中采用同一套装置以及同一只毛细管进行测定，因此，式中K为常数．在一定温度与压力下，选取蒸馏水和不同浓度的乙醇作为研究对象，分别进行测定得到一系列Δh数据，计算相应的γ值，并对γ-浓度(c)作图，选取不同的拟合函数，进行曲线拟合，对拟合曲线微分求微分值即在拟合曲线上均匀选取6～8个点分别做切线，求各点对应的一阶导数(dγ/dc)T,P值，其中T为开尔文温度．本实验最终需要求得每一个溶质分子所占据的横截面积(δB)，由Gibbs吸附等温式：

计算对应浓度下溶质分子的表面吸附量(Γ)．而在稀溶液范围内，Γ与c间的关系为：

以c/Γ-c作图，由经验方程的斜率的倒数求饱和吸附量(Γ∞)，最后求得δB．

2 实验结果

本研究是在室温为24.2℃，大气压为 100.68 kPa下进行，配制不同浓度的乙醇水溶液，分别移取6、12、18、24、30、36、42和48 mL无水乙醇，定容至100 mL．乙醇水溶液的浓度及测定的表面张力数据如表1所示．可知随着乙醇溶液浓度的增大，表面张力逐渐降低．由于需要从表面张力和浓度的关系得出表面吸附量与浓度的关系，因此采用Origin软件，选取3种不同的拟合函数对数据进行拟合，然后计算指定浓度的导数值，3种拟合函数分别为二阶多项式[γ=f(c2)]，四阶多项式[γ=f(c4)]以及对数[γ=f(lnc)]拟合，乙醇水溶液表面张力实验所需的参数结果列于表2．与之相应的3种不同拟合函数的γ-c关系如图1，可知3条拟合函数相关系数R2分别为0.973 5、0.986 8、0.985 1，拟合效果均较好．

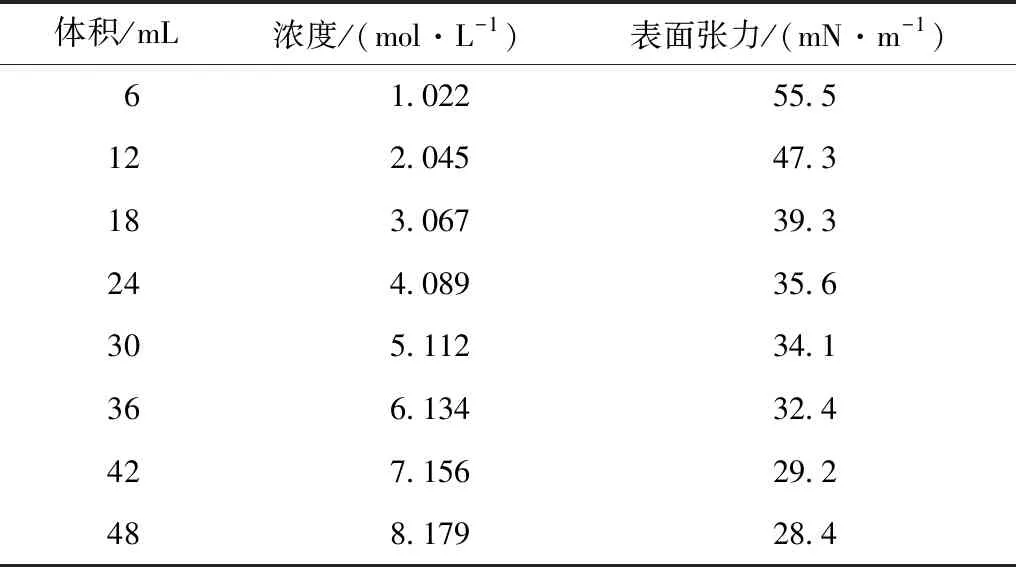
表1 乙醇水溶液的浓度及测定的表面张力

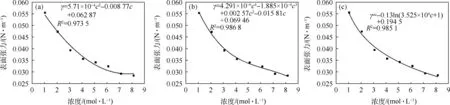
图1 3种不同拟合函数的表面张力与浓度关系图(a) 二阶多项式拟合；(b) 四阶多项式拟合；(c) 对数拟合

根据拟合函数所得的曲线，在曲线上均匀选取8个点，并分别做切线，所得切线的斜率即为(dγ/dc)T,P的值，进一步求得Γ和c/Γ．3种拟合函数所得数据列于表2中．从表2中的数据发现采用γ=f(c2) 拟合时，浓度为8.179 mol/L时得到的Γ与c/Γ均为负值，与实验理论不符，这是由于γ=f(c2)为抛物线所致，因此将第8组数据舍弃．通过Langmuir吸附等温式可知，c/Γ与c应呈现一种线性关系，所得直线的斜率的倒数即为饱和吸附量Γ∞．

根据表2中的数据所得的3种拟合函数c/Γ-c关系如图2所示，可知3条拟合函数相关系数R2分别为0.537 9、0.935 6、0.999 9，γ=f(lnc)拟合结果线性相关系性最好．

为了减少实验过程中由于人为因素造成的误差，将《物理化学实验》[8]教科书中所列出的25℃下的不同浓度的乙醇水溶液的表面张力采用同样的方法进行了拟合计算，3种不同拟合函数的γ-c和c/Γ-c关系如图3和4所示，可知R2分别为0.972 0、0.996 9、0.999 1和0.656 5、0.914 1、1，结果同样显示γ=f(lnc)拟合结果线性相关系性最好．

3 讨 论

曲线拟合是用连续曲线近似地刻画或比拟平面上散点组函数关系的一种数据处理方法．选择非线性函数进行拟合能较好的呈现出实验趋势，尽可能减少由于人为因素所带来的误差．本研究选取γ=f(c2)、γ=f(c4)和γ=f(lnc)等3种拟合函数进行相关参数拟合，结果显示采用γ=f(lnc)拟合所得的c/Γ与c的线性拟合相关系数达到了1，说明与实验数据拟合较好，相关性较高．此外，依据γ=f(c2)、γ=f(c4)和γ=f(lnc)拟合数据计算乙醇分子的横截面积分别为3.95×10-19、2.14×10-19和2.61×10-19m2，而直链醇的横截面积文献值为2.4×10-19～2.9×10-19m2[12]．因此，选取γ=f(lnc)拟合函数对实验数据进行后续处理，会相对减小数据处理所带来的误差，进而更接近于理论值．

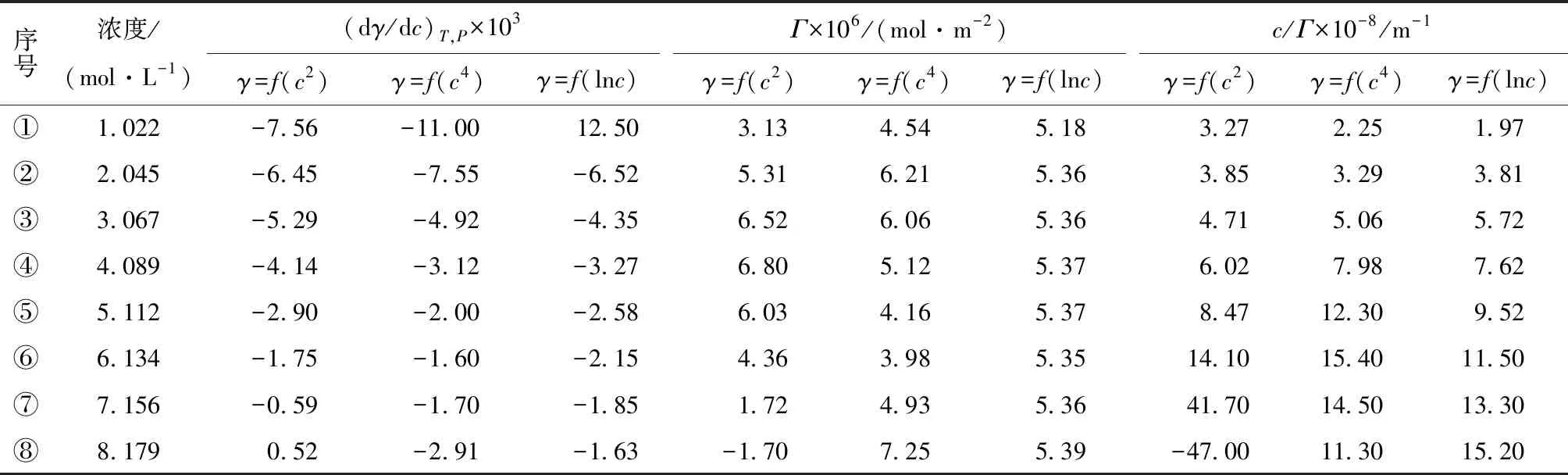
表2 乙醇水溶液的3种拟合参数值

注：γ为表面张力；c为浓度；(dγ/dc)T,P为表面张力与浓度的一阶导数；Γ为吸附量

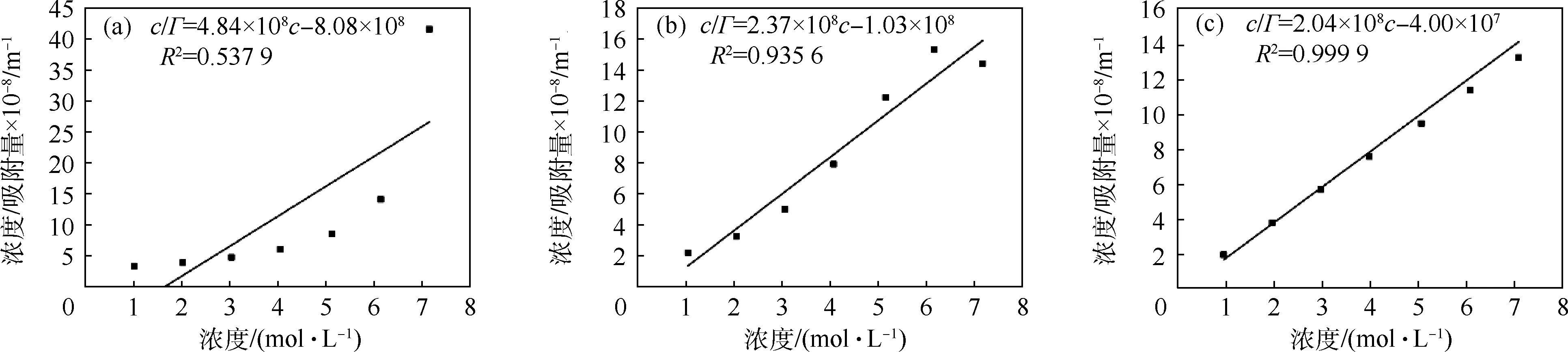
图2 3种拟合函数所得的表面吸附量与浓度关系图(a) 二阶多项式拟合；(b) 四阶多项式拟合；(c) 对数拟合

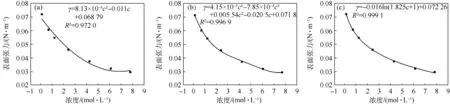
图3 25°时3种拟合函数的表面张力与浓度关系图(a) 二阶多项式拟合；(b) 四阶多项式拟合；(c) 对数拟合

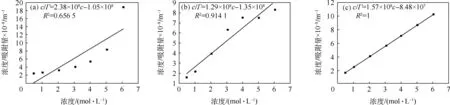
图4 25°时3种拟合函数所得的表面吸附量与浓度关系图(a) 二阶多项式拟合；(b) 四阶多项式拟合；(c) 对数拟合

4 结 论

在物理化学实验中，有关曲线的拟合是数据处理的关键之一，选取不同的拟合函数对数据进行处理会产生不同的误差.而选取非线形曲线拟合进行数据处理，可使实验数据处理更规范，同时能快速、准确地得到实验结果，提高实验效率.对于最大泡压法测定溶液的表面张力实验采用对数拟合的γ-c关系曲线能更好地体现出原始数据点的变化趋势，c/Γ-c线性关系更好，可有效避免数据处理过程中产生的误差，得到较为精确的实验结果，同时，筛选不同的拟合函数的过程还有助于学生提高解析数据的能力，进一步提高学生的综合素质.