基于TARCH(1,1)模型对石油价格波动的实证分析①
冯 超, 申世昌
(青海民族大学数学与统计学院,青海 西宁 810007)
0 引 言
近几年我国的发展速度非常迅猛,尤其是经济方面,一跃成为第二大经济实体。而石油对于人类来说越来越重要,无论是日常生活还是经济建设,石油在现在社会中扮演者重要的角色。国内外许多学者已经对石油的价格、需求量等一些因素进行了大量的研究。程立燕,李金凯通过建立TVP-VAR模型对石油价格的波动进行研究[1];吴孟琪采用STR非线性模型对石油价格的非对称性进行探讨[2];周宇利用ARIMA模型对石油价格进行预测[3];申雪峰对影响石油价格的经济因素进行了确定[4];孙怡然则是分析了经济增长对石油需求及价格的影响[5]。文中采用EViews7.2[6~7]通过建立TARCH模型对石油价格进行定量分析,来确定不同因素对石油市场变动的影响。
1 理论依据
1.1 ARCH模型
ARCH模型又叫自回归条件异方差模型,是用来描述一般均值方程的随机扰动项的条件方差的变化的。通常随机扰动项的平方服从一个q阶的ARCH模型:
ηt独立同分布,E(ηt)=0,D(ηt)=λ2,则模型为自回归条件异方差模型。
1.2 TARCH模型
TARCH模又叫门限ARCH模型,模型的方差方程为:
式中:dt-1是一个虚拟变量,当ut-1<0时,dt-1=1,此时非对称项存在;当ut-1>0时,dt-1=0,非对称项不存在。
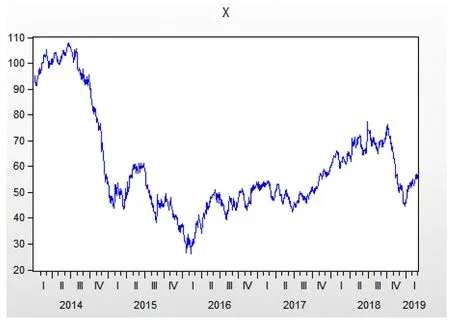
图1 2014年1月2日—2019年2月28日石油的价格走势
2 实证分析
选取卓创资讯石油网的石油价格,单位为美元/桶。样本区间为2014年1月2日到2019年2月28日。除去周末其及节假日,以及对缺失数据进行相应地补充,最终得到有效的数据为1346个。运用EViews7.2对数据进行实证分析。
2.1 数据处理
由图1可以看出,石油的价格在2014年年初时为100多美元/桶,但在15年底时价格已经跌破30美元/桶,石油价格在这一时间段内表现出明显地下降趋势,说明石油市场在这一时间段内受到了巨大的冲击。15年至19年期间石油价格呈现出小幅度地增长,尤其在18年价格达到了近几年的最高。从图中还可以观察到石油价格存在明显的非对称性与非平稳性。
将石油价格序列变为平稳序列,需要对该序列进行二阶差分,有效地消除趋势及其他因素的影响。
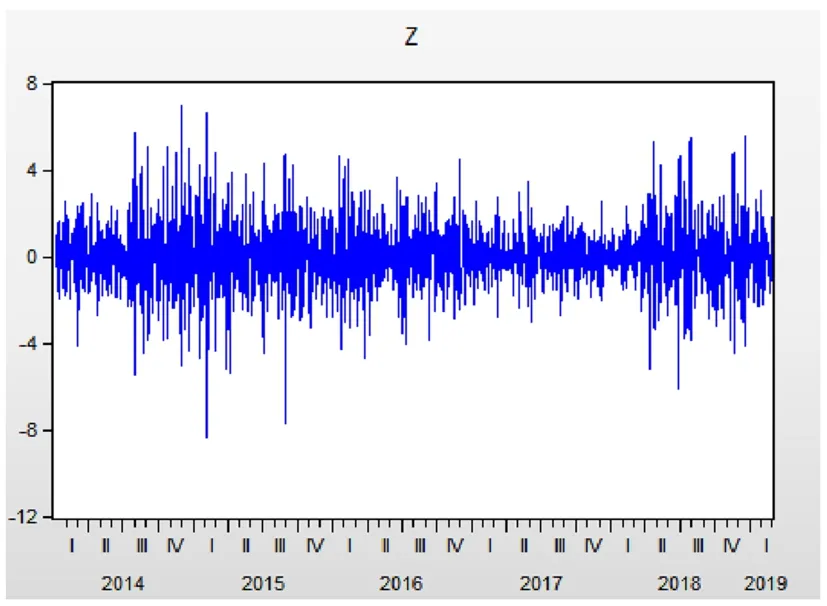
图2 石油价格的平稳图
由图2可知, 序列达到了平稳,还能看出序列存在明显的集群性与连续性,一个大的波动后面接着更大的一个波动,一个小的波动后面跟着一个更小的波动。
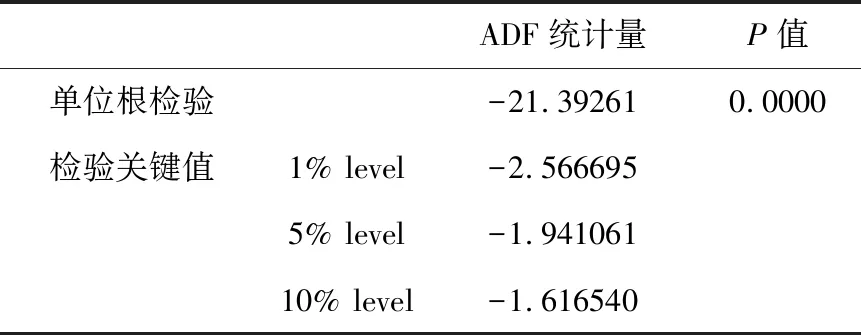
表1 石油价格序列的平稳性检验
由表1结果可知,序列通过了ADF检验,其中检验标准为无截距项与时间趋势项。ADF统计量为-21.39261,小于-2.566695、-1.941061、-1.616540;P值为0,说明此时的序列是平稳的,可以对该序列进行建模分析。
2.2 正态性检验
对序列计算各统计量。

图3 序列的统计量
由图3可知,序列的分布状况不同于正态分布。其均值为-0.028201,不为0,不满足正态分布的基本假设。偏度为-0.156229,说明序列左偏分布;峰度为4.860388,比正态分布的最大峰度值3要大,从而表现出尖峰的特征;J-B统计量的值为199.4339,其P值为0,进一步表明了该序列的分布与正态分布是有区别的。
2.3 ARCH效应检验
为了探究石油价格序列是否存在ARCH效应,首先需对该序列建立均值方程,通过对序列建立时间序列模型(ARMA模型),由序列的相关图可以判断出,序列满足ARMA(2,0)模型,由此可以建立模型的均值方程:
Zt=-0.708984Zt-1-0.346645Zt-2+μt
再对残差序列μt分别进行1阶、2阶的序列自相关检验,发现序列的P值接近于0,说明残差序列存在ARCH效应;假设序列在7阶的自相关检验时,LM统计量依然显著,说明序列可能存在高阶ARCH效应,如表2所示。

表2 序列μt的LM检验
表2中7阶自相关检验的P值仍为0,满足之前的假设。表明序列在高阶的自相关检验时依然存在ARCH效应,那么序列一定存在高阶ARCH效应,可以对残差序列建立ARCH模型。
2.4 模型识别
当残差序列μt在7阶自相关检验时依然通过,可以对该序列拟合GARCH模型。在1-7阶内ARCH效应非常显著,GARCH项可以为1,ARCH项也为1,那么可以拟合GARCH(1,1)。但是通过AIC、SC准则进行判断后发现GARCH(1,1)模型的拟合效果并不是很好,且从图1中可以观察出石油价格在14年向下有巨大的下跌,序列整体上呈现出非对称的特征。所以,应对残差序列建立TARCH、EARCH模型,来描述石油市场的波动状况。

表3 模型识别
由表3结果可知,TARCH模型的对数似然函数值更大,为-2256.888;而AIC、SC的值更小,为3.372411与3.395668。那么可以建立TARCH(1,1)模型来描述石油原油价格的波动。

表4 TARCH模型的参数估计
由表4结果可知,TARCH(1,1)模型中各系数的P值大多数为0,非常显著,可以认为TARCH模型效果很好。则建立其均值方程与方差方程:
均值方程:Zt=-0.703686Zt-1-0.357517Zt-2+εt
方差方程:
在方差方程中,α=0.102529、γ=-0.085770。当有好消息时(ut-1>0),dt-1=0,非对称项不存在,只有一个0.102529倍的冲击;有坏消息时(ut-1<0),dt-1=1,非对称项存在,会有一个0.016759倍的冲击。因为γ<0,非对称效应的作用使得波动减小。
2.5 残差项的适应性检验。
通过分析确定建立TARCH(1,1)模型之后,需要对模型的均值方程残差项εt进行ARCH效应检验,已确定建立的模型是否合适。对TARCH(1,1)模型进行ARCH-LM检验,结果如表5。

表5 序列εt的适应性检验
由表5结果可知,均值方程残差项εt的LM检验的P值为0.5757,与显著性水平为5%的值相比要大,表明残差序列独立,没有 ARCH效应;即石油价格序列满足TARCH(1,1)模型,并且可以有效地说明石油市场的波动状况。
3 结 论
通过对选取的数据区间进行实证分析后发现,石油价格在14年经历了大幅下跌后,近4-5年内有稳步回升的迹象。此外,对石油价格残差序列进行ARCH效应检验以后,发现序列存在明显的“尖峰后尾”的现象;而且残差序列存在高阶ARCH效应,通过进一步分析之后发现,残差序列还存在非对称现象,且十分显著,对序列建立了TARCH(1,1)模型。由模型的参数估计可知,模型的非对称系数为负,会使石油价格的波动逐渐减小;而出现好消息时,对石油价格的冲击要比出现坏消息时的冲击更大,但最终这种波动会逐渐地趋于平稳。
由上述的实证分析后,可以更加清楚地认识到石油市场受不同因素的影响而产生的现象也不相同;通过对具体现象的分析,可以制定相关的措施来调控石油价格,进而加快我国的现代化建设。

