永磁同步风力发电机的时滞补偿自抗扰控制设计

朱超威, 李生权, 李 娟, 吴远网, 鲁 玲

(扬州大学水利与能源动力工程学院, 江苏 扬州 225127)

风能因具有洁净、丰富和分布广泛等优势而成为重要的能量来源．近年来, 各国对风力发电的发电效率和发电质量提出更高的要求．直驱式永磁同步风力发电机(permanent magnetic synchronous generator, PMSG)系统由于省去齿轮箱而具有运行噪声小和运行效率高等优点[1]．随着该类型风电系统被广泛使用, PMSG的转速跟踪和最大功率输出问题也备受关注．Li等[2]提出将模糊算法与PID相联合的方式,自动整定PID参数以维持风力发电系统在最大功率点运行; Hong等[3]基于遗传算法设计了一种针对PMSG的自适应占空比法,使得PMSG在可变速度下运行实现最大功率跟踪,但该算法的编程较为复杂,难以在线实现; She等[4]基于空气动力学针对分层配置下的风力发电系统提出一种自适应神经网络算法,但该算法计算量大且需要相当多的数据训练．由于风电机组所处环境恶劣,受雨雪天气影响严重,机组老化也会导致电感和电容等参数变化,从而引起系统模型不确定性等问题,故上述方法在实际运行中会遭遇一定困难．本课题组前期工作[5]设计的线性自抗扰控制器对于PMSG的最大功率跟踪表现出结构简单、追踪快速和抗干扰能力强等优点．自抗扰控制算法[6](active disturbance rejection control, ADRC)的核心是扩张状态观测器(extended state observer, ESO),主要用于估计各阶状态变量以及总扰动．该算法不依赖于精确数学模型,易于工程实现且抗干扰能力强,已被广泛应用于多个领域的研究[7-10]．然而,风力发电系统的内部控制器存在着计算时延、传感器响应时延以及机械耦合和传输特性引起的时延,导致控制系统中产生相位滞后,若不校正将破坏系统的稳定性,从而影响ADRC的风能捕获控制性能．针对上述问题,本文拟利用Smith预估器结合对象模型进行变量预估,将时延环节移到闭环之外,补偿系统运行过程中的时滞,使得自抗扰控制器作用于无时延环节并调节参数以期获得较好的控制品质．

1 永磁同步风力发电机及风力机的建模

1.1 风力机数学模型

基于传统的空气动力学, 自然风的风能由风力机叶片吸收后转变为机械输出功率,两者之间的数量关系[11]如下:

Pm=0.5ρπr2CP(λ,β)v3,

(1)

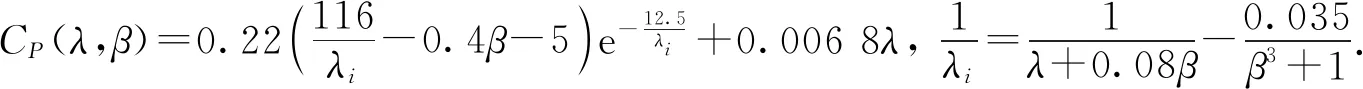
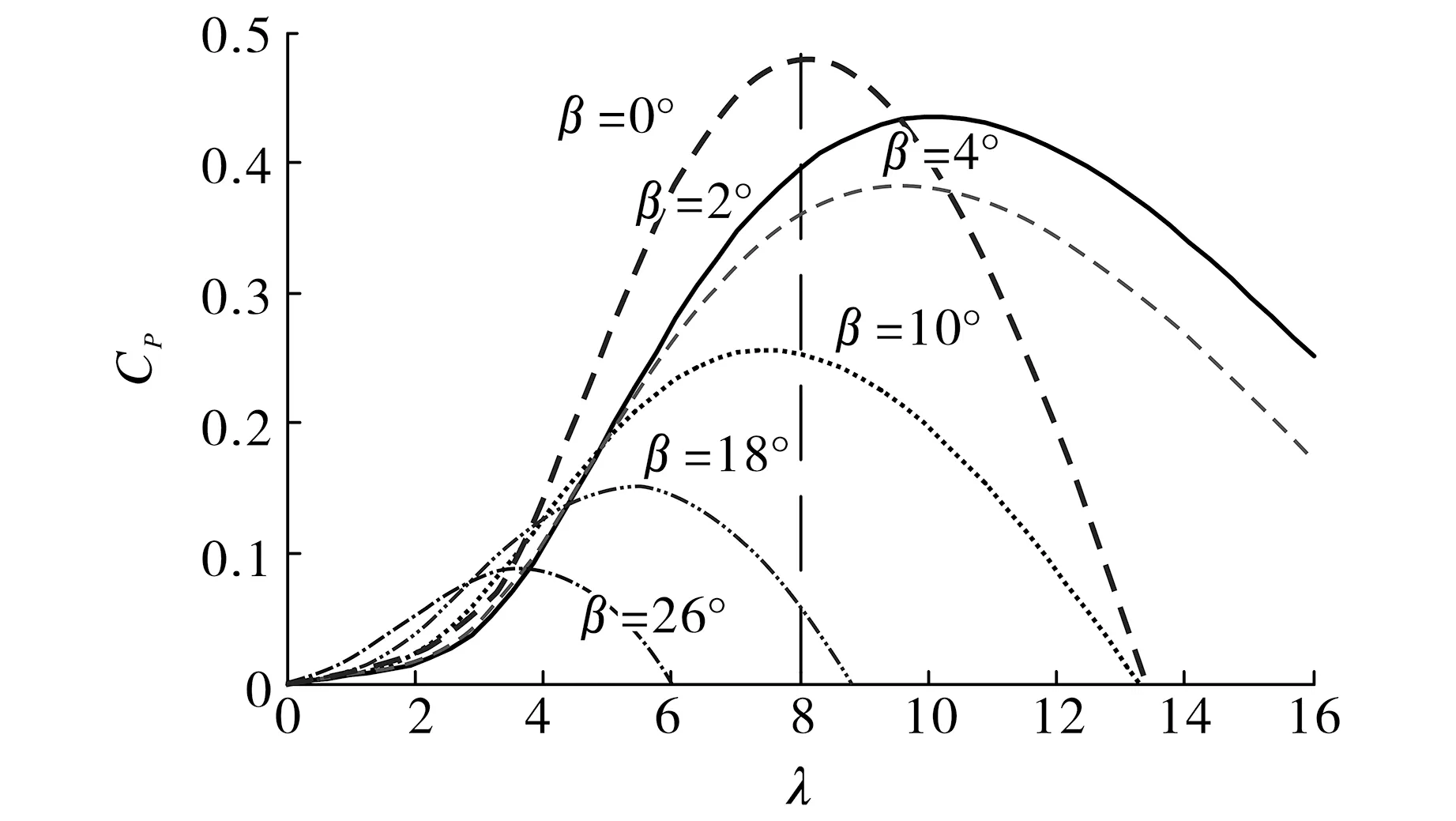
图1 风力机叶尖速比与功率系数的关系曲线Fig.1 The relation curve between wind blade tip speed ratio and power factor

为了使风能得到最有效的利用, 须使风力机转速ω与风速v之间维持最佳叶尖速比,进而使得功率系数CP最大．图1为不同的桨距角对应的叶尖速比与功率系数的关系曲线．由图1可见,当β=0°时,调整风力机的转速使其稳定运行在最佳叶尖速比状态(即λ=8下), 此时对应的最大输出功率系数CP=0.48．根据式(1)可知风力机在该状态下可以捕获最大输出功率．

1.2 永磁同步风力发电机数学模型

PMSG在旋转d-q坐标系下的数学模型[12]可描述为

(2)

其中ud,uq为d-q轴上的电压分量;id,iq为d-q轴上的电流分量;ψf为永磁体磁链;n为电机极对数;Ld,Lq为d-q轴上的电枢电感分量;R为电枢电阻．

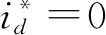
Te=1.5nψfiq,

(3)

于是发电机系统动态方程为

Jdω/dt=Tm-Te-Bω,

(4)

其中J为转动惯量,Tm为驱动转矩,B为黏性摩擦系数．

2 基于时滞补偿的自抗扰控制器设计

2.1 自抗扰控制器设计

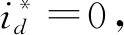
本文的ADRC控制律为u(t)=kp(ω*-z1)-z2/b, 其中kp为比例增益,ω*为参考转速,b为NESO的观测增益．

2.2 Smith预估器设计

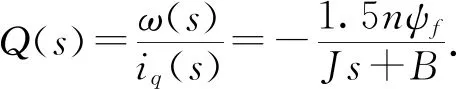
由于在系统运行过程中的各种时延不可避免, 设总时延为τ, 可得转速环实际频域模型

(5)

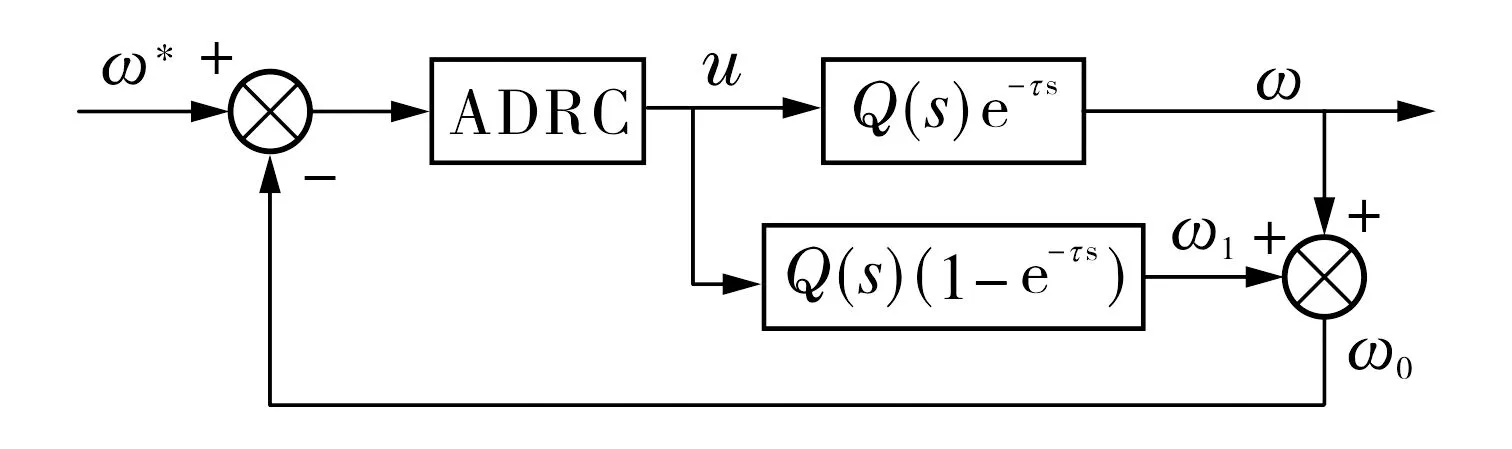
图2 Smith预估器结构示意图Fig.2 Schematic diagram of Smith predictor

为了使控制器作用于对象无时延部分, 现根据Smith预估器的原理, 引入中间变量ω0=ω+ω1=Q(s)e-τsu+Q(s)(1-e-τs)u=Q(s)u, 其中ω1是Smith预估器输出．改进后的Smith预估器结构如图2所示．

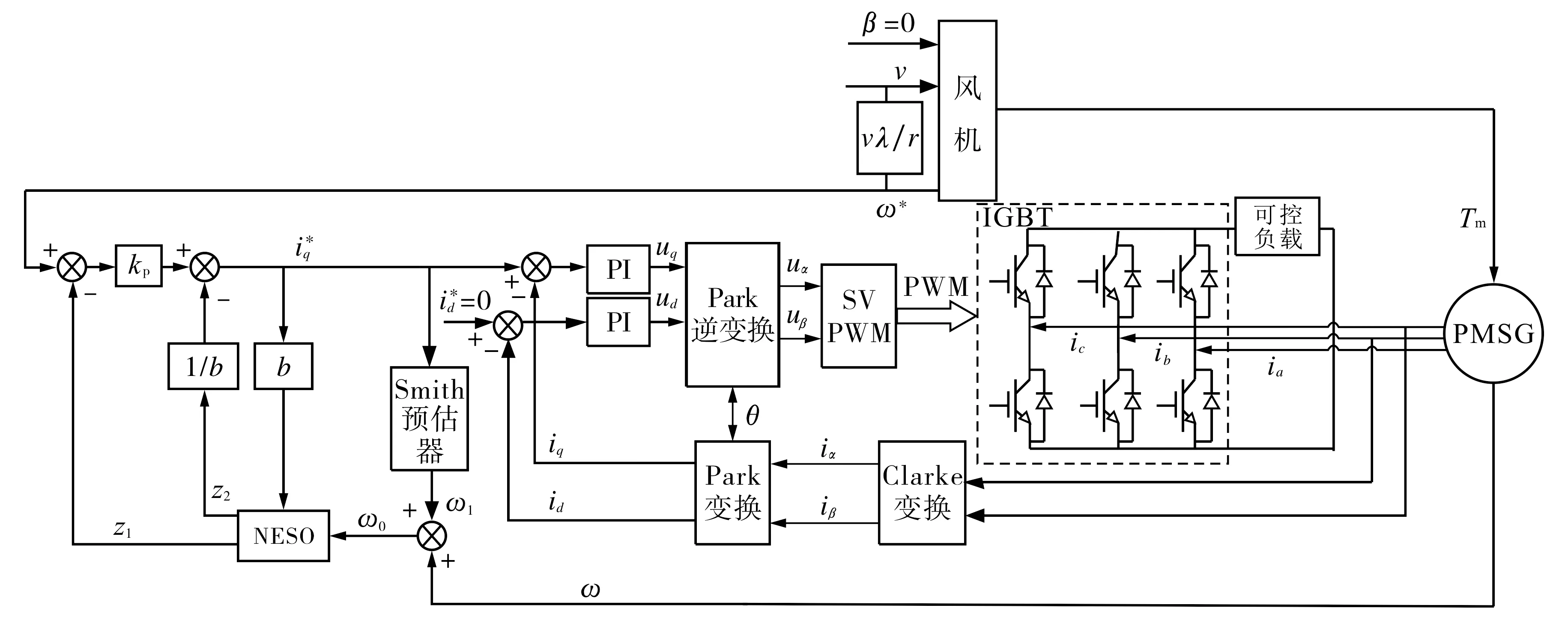
图3 永磁同步风力发电控制系统示意图Fig.3 Schematic diagram of PMSG control system

3 仿真分析

为了验证本文所设计控制器的有效性,笔者通过Matlab/Simulink软件对传统的ADRC控制与本文控制方法进行仿真分析,结果如图4所示．

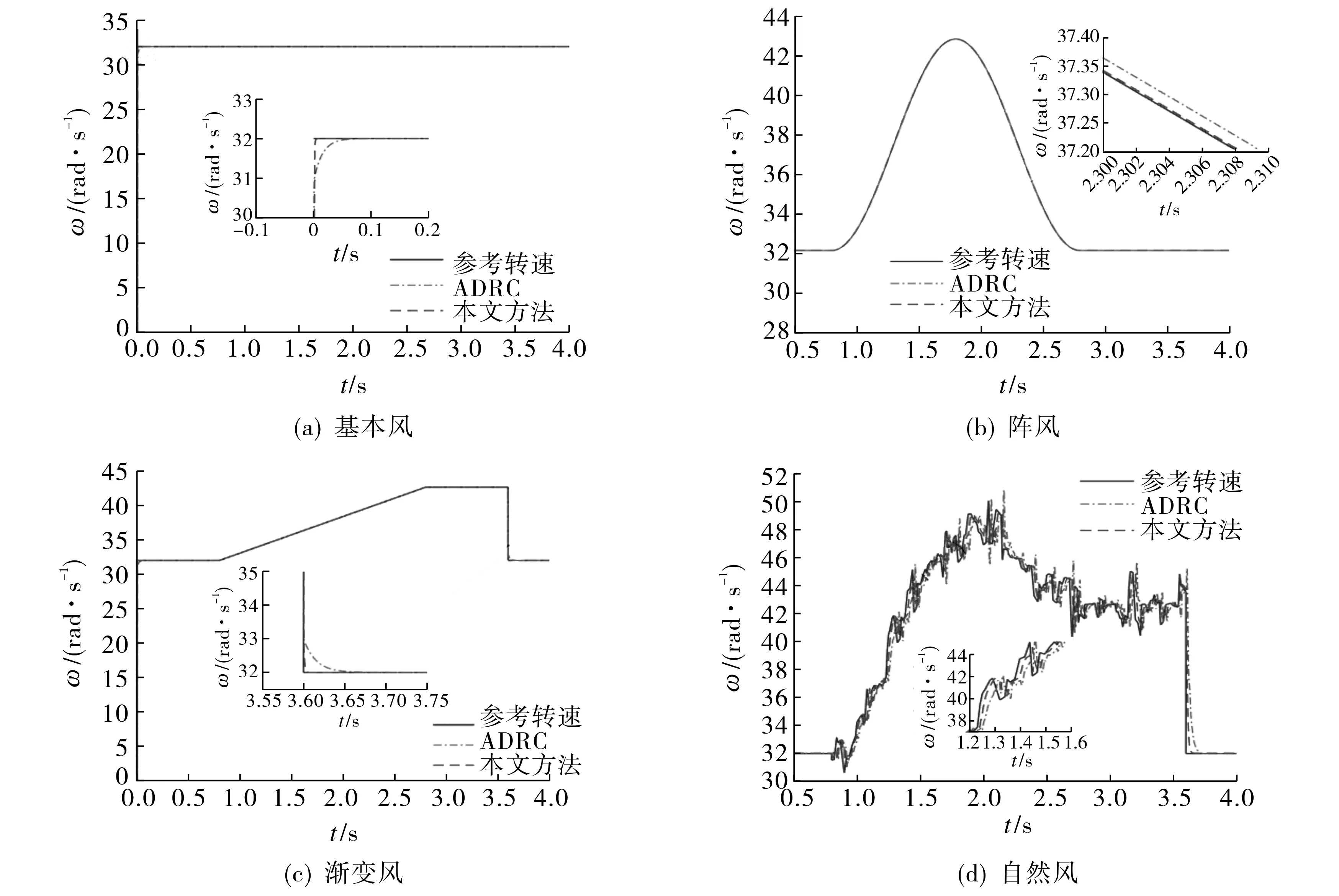
图4 不同风型下PMSG转速跟踪性能Fig.4 PMSG speed tracking performance under different wind types

调节永磁同步发电机参数: 额定转速ωr=3 000 r·min-1, 电枢绕组电阻R=2.875 Ω, 转动惯量J=1×10-3kg·m2, 黏性摩擦系数B=8.29×10-5kg·m2·s-1, 极对数n=4, 永磁体磁链ψf=0.175 Wb, 电枢绕组电感L=8.5×10-3H; 风力机参数: 空气密度ρ=1.25 kg·m-3, 风力机半径r=1.5 m, 最大功率利用系数CP=0.48, 最佳叶尖速比λ=8, 基本风速v=6 m·s-1, 时延常数τ=30 ms．

图4为不同风型[7]下的PMSG转速跟踪性能．由图4可知: 1) 基本风下采用本文控制方法的PMSG转速跟踪的调节时间更短,控制效果更好; 2) 阵风下本文控制方法的PMSG的转速更加贴合参考转速, 稳态误差小, 对风能的利用效率高; 3) 渐变风下当PMSG跟踪至第3.6秒处风力急速减弱时, 传统的ADRC显示出0.05 s的缓冲, 而本文控制方法的跟踪更直接,系统响应更加快速; 4) 自然风下由于Smith预估器能有效减小系统中时延的影响, 故PMSG转速在跟踪参考转速的多处拐点时更加平滑, 抗干扰能力更强．

综上所述, 本文提出的基于时滞补偿的自抗扰控制方法无论在抗干扰能力还是动态性能方面均优于传统ADRC．NESO与Smith预估器的结合不仅实现了风力发电系统的最大功率输出,而且能加快系统响应,从而提高PMSG的转速跟踪性能．