客车车身骨架静态特性分析及优化

方学良, 陈靖芯, 景 科, 姜欣悦

(扬州大学机械工程学院, 江苏 扬州 225127)

客车车身不仅要承载客车各部分的重量, 还要承受各方面的载荷．为了满足安全要求, 通常采用加厚局部杆件的方法增加强度,从而导致车身局部强度、刚度富裕．客车轻量化[1-3]不仅能减少制造的成本,还能达到节能减排的目的．范文杰等[4]采用多刚度拓扑优化的方式对某客车车架进行结构轻量化设计, 有效增加了车架的扭转和弯曲柔度, 但无法确定杆件的厚度尺寸, 优化后车架质量没有明显下降; 苏瑞意等[5]采用多学科协同的方式对客车进行优化设计, 但有限元模型复杂,优化成本过高．本文拟采用基于灵敏度分析的优化方法, 对某全承载式客车车身骨架进行轻量化设计, 以期在满足强度和刚度基本性能的前提下尽可能降低车身骨架的质量．

1 有限元模型

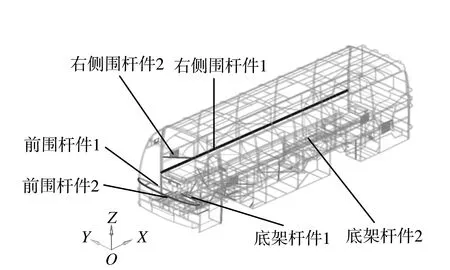
图1 客车骨架有限元模型Fig.1 Bus skeleton finite element model

客车车身骨架采用板壳单元, 单元尺寸为5 mm, 在Hypermesh中用共节点方式或RBE2刚性单元模拟焊接, 用Bolt单元来模拟螺栓连接, 客车车身骨架共有节点3 525 872个, 各类单元3 585 072个,其中四边形单元3 530 028个, 三角形单元55 012个, 刚性单元5 257个．图1为所建有限元模型．

客车静态特性分析时, 车身骨架自重以惯性力方式施加; 顶盖、空调和底盘各总成重量在相应的质心位置施加质量单元, 并用RBE3单元与具体安装位置节点相连; 乘客、司机及座椅重量和行李仓行李重量以均布载荷方式施加．车身骨架材料为Q345钢, 具体参数为: 弹性模量为210 GPa, 泊松比为0.3, 密度为7.8 g·cm-3, 屈服强度为345 MPa, 强度极限为600 MPa．

2 结果讨论

2.1 典型工况下静态特性分析

客车在行驶过程中若遇到突发事件采取紧急制动, 车身骨架会受到巨大的载荷, 在紧急制动工况下,客车最大制动加速度一般为0.8g[6]; 而在凹凸不平的路面上行驶时, 客车会出现一个车轮瞬时悬空的情形,此时客车受到非对称载荷作用, 当右后轮悬空时扭矩较大,受载情况较为恶劣．本文选取紧急制动和极限扭转右后轮悬空2种典型工况进行静态特性[7]分析．在紧急制动工况下, 选取左前轮X、Y、Z，右前轮X、Z, 左后轮Y、Z, 右后轮Z方向对悬架装配处节点进行约束; 在极限扭转右后轮悬空工况下,只需在紧急制动工况的基础上释放右后轮Z方向自由度．

2.2 客车车身骨架强度和刚度

图2(a)是紧急制动工况下客车的右侧围骨架应力分布云图．由图2(a)可知, 车身骨架最大应力出现在右侧围中间立柱的焊接处, 最大应力为208.9 MPa．图2(b)是极限扭转右后轮悬空工况下客车右侧前纵梁骨架局部应力分布云图．由图2(b)可知,车身骨架最大应力位于右侧前纵梁骨架的钢板弹簧连接处,最大应力为290.7 MPa．客车车身骨架所使用的材料Q345钢的屈服强度为345 MPa, 因此2种工况均满足强度要求．

紧急制动工况下客车车身骨架结构总位移变形图如图2(c)所示．由图2(c)可知, 该工况下车身最大变形位于最后排座椅处,最大变形量为6.297 mm．极限扭转右后轮悬空工况下车身骨架结构总位移变形图如图2(d)所示．由图2(d)可知, 该工况下最大变形区域主要集中在车身骨架后侧的右半部分, 其中后围、右围与顶围骨架的连接区域出现最大变形,最大变形量为23.857 mm, 该工况是客车行驶中的极限工况,较大的变形量是由于右后轮悬空失去约束变形累计造成的,与实际情况相吻合．

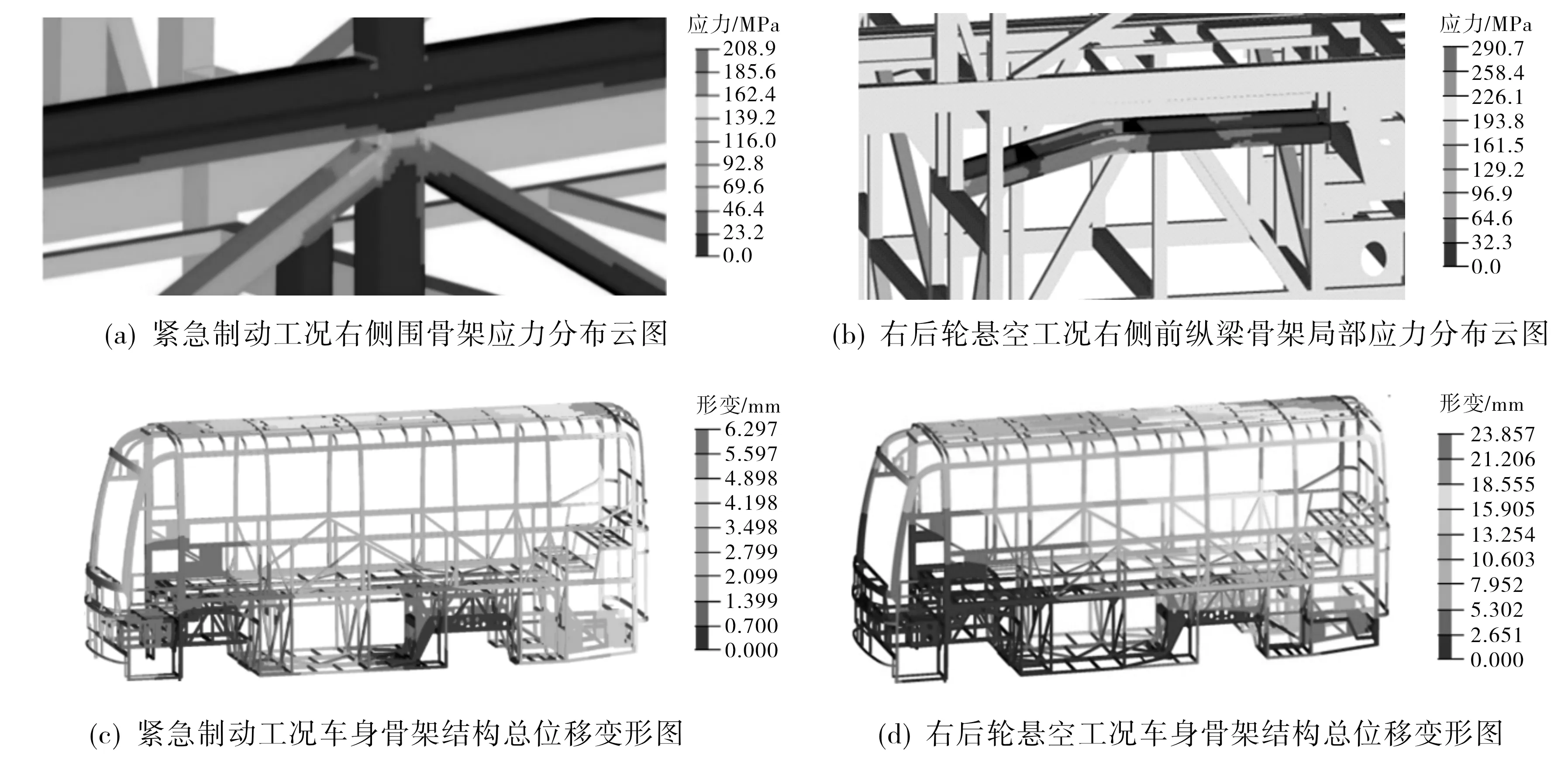
图2 2种典型工况下车身骨架的应力分布云图和总位移变形图Fig.2 The stress and displacement nephogram of body frame structure under two typical conditions

2.3 客车车身骨架应力测试

为验证有限元模型计算的正确性及有限元分析的可靠性, 根据有限元分析结果及客车实际使用的情况, 在应力集中区和受力变形较大的区域共布置了42个测点, 采用电阻应变片进行应力测试[8]．布置的测点如图3所示．各点静态应力σ=Eε, 其中E为弹性模量,ε为应变值．通过计算将所测得的应变换算成应力, 并将其与有限元模拟计算值进行对比,部分数据如表1所示．从表1结果可以看出, 有限元分析结果与试验数据的相对误差均小于10%, 验证了有限元模型的可靠性．

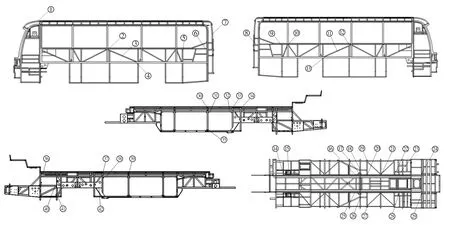
图3 测点位置分布图Fig.3 Distribution of measuring points

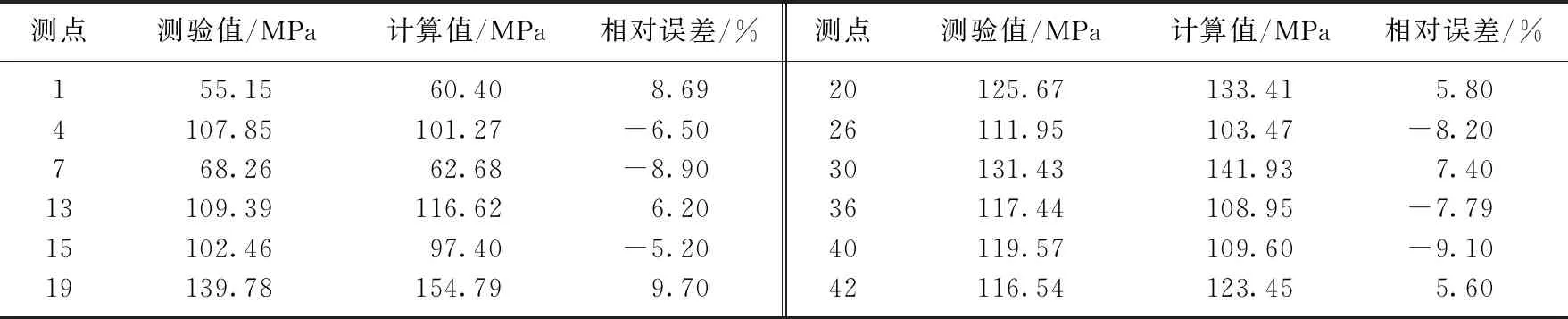
测点测验值/MPa计算值/MPa相对误差/%测点测验值/MPa计算值/MPa相对误差/%155.1560.408.6920125.67133.415.804107.85101.27-6.5026111.95103.47-8.20768.2662.68-8.9030131.43141.937.4013109.39116.626.2036117.44108.95-7.7915102.4697.40-5.2040119.57109.60-9.1019139.78154.799.7042116.54123.455.60

3 客车车身骨架轻量化设计

3.1 优化模型

2) 约束条件. 以低于Q345钢的最大应力作为约束条件, 即车身骨架的最大等效应力σmax<345 MPa．

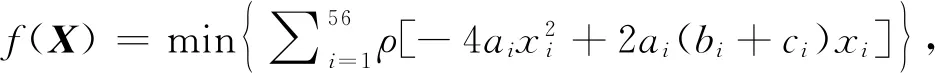
3.2 基于灵敏度分析的优化

本文运用基于灵敏度[9-10]分析的优化方法计算车身的质量和应力对杆件厚度x的灵敏度, 对质量和应力都较为敏感的杆件, 计算出质量对于应力的相对灵敏度,若该比值为正数,则表示车身质量减小会使应力降低, 该值越大说明在减小车身质量的同时应力降低得越快;若该比值为负数,则表示车身质量减小会使应力增大,该值越大说明在减小车身质量的同时应力增加越快．以上限值为初始条件优化得到的部分杆件灵敏度结果见表2．从表2可以看出,除右侧围杆件1不变外, 其余杆件厚度均变小．经灵敏度分析优化,车身总质量下降了87.0 kg,减重率达5.04%．

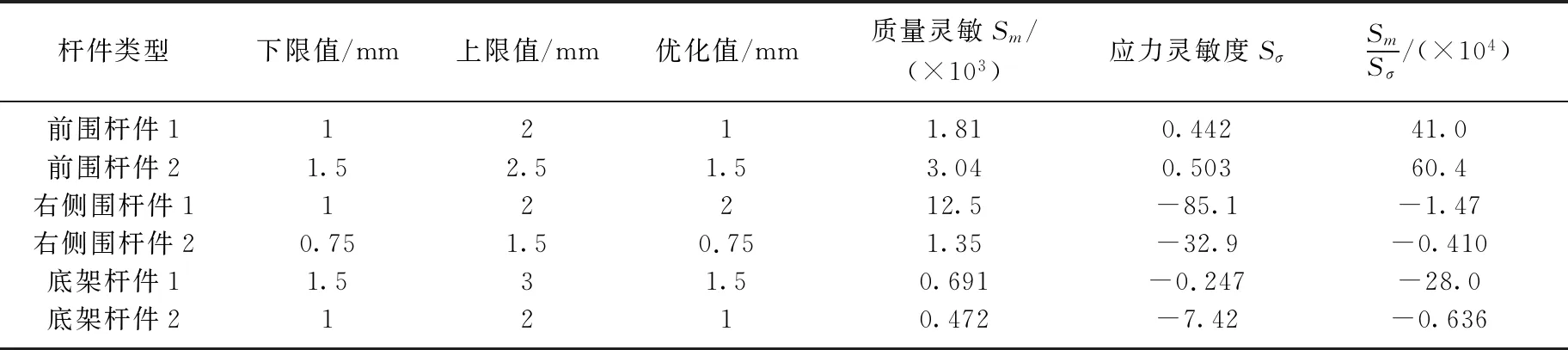
表2 部分杆件灵敏度分析结果Tab.2 Sensitivity analysis results of some bar parts

为了验证灵敏度分析车身骨架的正确性, 对优化后的有限元模型进行静态特性分析．轻量化前后的客车车身骨架应力和应变对比结果见表3．表3结果显示, 优化前后各工况最大应力和变形的变化均不显著, 说明轻量化后客车的应力和变形都在合理的变化范围之内,优化后客车车身骨架符合行驶要求．

表3 轻量化前后各工况最大应力和变形的对比Tab.3 Comparison of maximum stress and deformation in different working conditions before and after lightweight